面向电网辅助服务的虚拟储能电厂分布式优化控制方法

王 枭，何怡刚，马恒瑞，汪增勇

（1. 武汉大学电气与自动化学院,湖北省武汉市 430072；2. 青海大学新能源光伏产业研究中心,青海省西宁市 810016；3. 武汉理工大学自动化学院,湖北省武汉市 430070）

0 引言

开发利用可再生能源是降低电力系统碳排放的有效途径。考虑到近年来国际上几次重大停电事故,传统电网调控方式无法完全适应可再生能源高占比的新型电力系统,电网的稳定运行再次成为研究热点。以小型屋顶光伏发电为代表的可再生能源系统在配电网中广泛接入,导致节点电压波动明显。在输电网层级,大型风电场、光伏电厂大量投产并网,其发电间歇性与不确定性使电网整体的功率平衡变得愈加困难。在此背景下,储能被视为未来智能电网的重要支持技术,可为电力系统提供频率、电压支持等辅助服务,有效提高了风、光等可再生能源的消纳水平［1］。

早期的电力系统储能多采用大规模的集中式储能技术,由于受到地理条件等因素的限制,近年来用户侧分布式储能占据储能技术发展的主导地位。作为需求侧响应重要的功率来源,分布式储能具有容量小、数量规模大等特点［2］。2019 年底,国家发改委、国家能源局联合发布关于深化电力市场建设意见,鼓励储能设施等第三方参与电力系统辅助服务［3］。如何协调这些覆盖辽阔地理区域的多元化、分布式储能设备,为电力系统提供快速、有效的调频、调压等服务,是规模化储能资源利用要解决的重要问题。

低压配电网中的分布式储能单元可聚合为虚拟储能电厂,同大容量抽水蓄能电站一样受系统运营商（system operator,SO）调度,参与电网日常运行［4］。虚拟储能电厂的聚合控制一般采用集中式结构［5］,由控制中心监控区域内所有的分布式储能单元。考虑未来电网中大量的可用储能资源,集中控制将产生高昂的通信成本,控制中心的数据吞吐量大、计算负担重,难以接近实时地给出储能设备控制指令,无法适用于超大规模分布式储能的并网控制。采用相邻通信原则的分布式控制具有抗扰性强、扩展性好、即插即用和保护隐私等优点［6］,更适合分布式储能的协调调度。

在分布式控制结构中,通过信息网互联的储能设备被视为具有决策能力的智能体,一致性控制是多智能体网络的主要控制方法［7］。现有研究多利用一致性控制实现分布式电源（distributed generator,DG）间的功率均分,或用于储能单元间的荷电状态（state of charge,SoC）平衡［8-9］；文献［10-12］采用主-从一致性方法调整一致性平衡点,使DG 集群具有主动调节电网频率、电压的能力。此类方法的优点是简单、易于实施,但存在以下两方面的不足:1）主-从一致性控制只能实现对配电网特殊节点的电压支持,无法保证所有节点的调压效果；2）一致性控制只能依靠限幅环节解决DG 的多种运行约束,此时系统的整体稳定性难以评判。相比之下,分布式优化方法灵活性更高、适用性更广,优化问题建模能够兼顾辅助服务与储能单元约束条件,优化问题求解可利用多智能体的群体决策能力,对协同大规模储能设备具有明显优势［13］。

大量现有研究将分布式优化方法用于DG 的协同优化调度。文献［14］利用次梯度下降法实现了虚拟电厂的聚合功率控制；文献［15］基于交替方向乘子 法（alternating direction method of multipliers,ADMM）,给出了超大规模储能单元的分布式协同优化方法,并考虑了多种储能操作约束；文献［12,16］利用增量成本一致性实现了虚拟储能电厂的经济调度,并分析了网络攻击下分布式控制的鲁棒性［16］。但是,上述研究一般忽略承载DG 配电网的网络结构,并未考虑DG 出力对配电网节点电压的影响。实际上,由于配电网系统较高的电阻/电抗（R/X）值,DG 调度产生的有功潮流将显著影响配电网电压,有研究据此利用变流器灵活的功率控制实现配电网的局部潮流管理与电压调节。例如,文献［17］提出了一种基于原始-对偶算法的分布式电压控制,通过调整变量迭代方向,在保证原始变量下降的同时,得到了完全分散式的控制率；文献［18］提出了基于ADMM 的电压支持方法,对原始优化模型引入了一致性约束条件,得到完全分布式的电压控制。相比于原始-对偶等一阶优化算法,ADMM在实际应用中往往体现出更好的收敛性与抗扰能力［19］。

在上述分布式优化调度与电压控制研究基础上,仅有少部分文献考虑分布式储能集群跟随电网调控信号,如调峰、自动发电控制（automatic generation control,AGC）,并同时提供配电网电压支持。文献［20］将配电网整体视为虚拟电厂,采用基于原始-对偶的分布式控制方法,使虚拟电厂能够响应电网调控信号,同时考虑了配电网的潮流管理；文献［21］关注配电网公共连接点处功率注入与电压支撑的控制方案,该方法基于一致性算法,须人为将相邻DG 划分为具有特定控制目标的群落。

针对输、配电不同层级的控制目标,本文提出了一种适用于规模化储能设备的完全分布式自治控制方法,使虚拟储能电厂能够快速跟随系统运营商给出的调控指令,参与输电网等级的功率平衡,同时为配电网提供局部电压支持,适用于要求储能快速响应以平抑可再生能源出力影响的应用场合。该控制方法基于模型预测控制（model predictive control,MPC）［22］与分布式优化方法:首先,建立具有广泛适用性的优化问题模型,考虑到储能、电网的多种约束与问题的时空耦合特点,将优化问题嵌入MPC 框架内,针对未来一段时间范围滚动求解；其次,推导集中式MPC 优化问题的分布式求解方法,在原始优化问题的对偶形式中引入一致性约束条件,实现了完全分布式的储能设备最优调度；最后,仿真算例采用典型配电网系统,验证了可再生能源接入情况下,虚拟储能电厂分布式控制框架的有效性。

1 系统建模

1.1 配电网

本文主要考虑配电网电压稳态模型,由潮流方程描述,其拓扑结构一般通过图论模型Gn=(N,En)给出。对有向图Gn,N表示配电网中除公共连接点外所有节点的集合,En表示所有配电线路集合,N中元素的个数为N。典型的配电网一般具有辐射状结构,可采用线性的DistFlow 模型构建线路潮流与节点电压幅值关系［17］,即对∀i,j∈N,(i,j)∈En,有

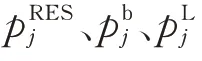
式（1）至式（3）的潮流方程可用如下向量形式表达［17］:

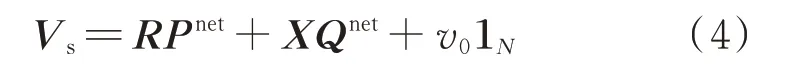
式中:Vs∈RN为系统中所有节点电压组成的列向量；Pnet、Qnet∈RN,分别为节点有功、无功注入组成的列向量；v0为配电网公共连接点处的电压；1N表示长度为N、所有元素为1 的列向量；R和X分别为系统的电阻、电抗矩阵。

系统的电阻、电抗矩阵R和X可由下式得到:

式中:M为Gn的关联矩阵；Dr和Dx分别为所有线路电阻、电抗组成的对角矩阵；M-T表示M的逆并转置。考虑到一般中低压配电网较高的R/X值,这里仅考虑储能系统的有功支持。

1.2 信息网

与配电网相似,信息网络采用图论模型Gc=(S,Ec)描述,S中的每个元素代表储能单元,Ec中元素表示储能设备间的通信链路。模型Gc的特征矩阵包括邻接矩阵Ac和拉普拉斯矩阵Lc,可根据图论模型拓扑结构获得,这里假设通信网络Gc为无向的连通图。

1.3 储能系统

研究储能的电网侧应用一般可忽略变流器的暂态过程,采用通用的储能系统模型,表示储能的功率与能量变化。对于∀i∈S,有

2 基于MPC 的虚拟储能电厂优化问题建模

调度配电网中的分布式储能须考虑问题的时间、空间耦合特性,MPC 为系统解决储能资源的优化配置提供了有力工具。MPC 基于最优控制理论与数值优化方法,利用系统模型对未来控制输入与运行轨迹进行预测与优化,间隔相同时间重复进行,其稳定性、最优性与鲁棒性等相关理论已较为完备［22］。优化问题建立的目标是将分布式储能聚合为虚拟储能电厂,为电网提供有功支持。因此,针对未来一段时间范围t=0,1,…,H-1（H 为预测时域长度）构建优化问题模型如下。

3 虚拟储能电厂MPC 优化模型分布式求解

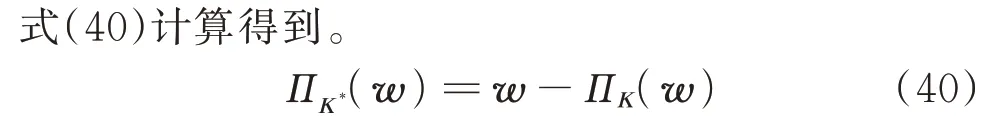
由此可知,式（34）至式（39）中的改进ADMM算法实现了MPC 优化问题的完全分布式求解,每个控制周期内各储能智能体仅须与相邻的储能单元通信,即可解决虚拟储能电厂的协同功率跟随与电压控制问题。

4 仿真算例

为了验证所提出的虚拟储能电厂控制框架在分布式储能优化调度中的有效性,本文在IEEE 33 节点系统（算例1）与119 节点系统（算例2）对储能的控制效果进行分析,比较了集中优化与分布式优化方法的调度结果,对电网的电压控制效果进行了分析。附录A 图A1 展示了IEEE 33 节点系统内的虚拟储能电厂示意图,聚合商的职责是接收电力系统运营商的服务控制请求,只须与配电网中的小部分储能单元进行通信。图A2 为算例2 中119 节点系统拓扑结构示意图。

4.1 仿真设置

储能单元的额定参数,即额定功率、额定能量、充电效率、运行成本系数（参见优化模型式（8）至式（16））从给定的范围内随机产生,如表1 所示。储能设备的初始SoC 设置为0.5,允许的SoC 范围为0.1～0.9,充、放电效率取值相同,自放电系数αi取为0。对于i∈{1,2,…,N},储能单元的通信网络Gc具有环状结构,每个储能单元可以同最近的6 个储能单元通信。仿真实验中,算例1、2 的配电网中分别随机接入11 台和39 台光伏发电系统,光伏出力由文献［26］中提供数据获得。此外,系统中负荷功率变化表示为系统原始静态负荷叠加时变偏移量,附录A 图A3 显示了24 h 内11 台光伏系统与10 台有功负荷的功率变化情况,采样周期为5 min。

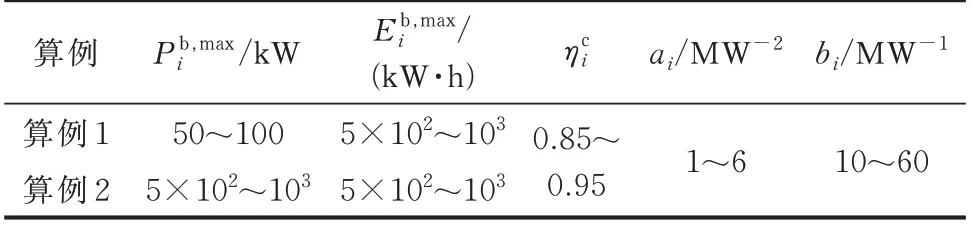
表1 储能单元参数Table 1 Parameters of energy storage units

设算例1 中节点电压的允许范围为0.95～1.05 p.u.,算例2 节点电压允许范围为0.99～1.01 p.u.,公共连接点处的电压幅值均为1.01 p.u.。本文中的分布式MPC 算法采用MATLAB 实现,利用MatPower［27］对电网交流潮流进行模拟。

针对本文所采用的改进型ADMM 算法,设ρ=σ=0.001,算法的循环退出条件为:

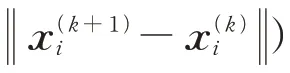
4.2 算例1

首先,比较了储能集群响应电网功率请求时对节点电压造成的影响,如图1 所示。在不考虑电压控制情况下,储能单元调度使配电网节点电压畸变更明显、电压越限更严重,由此可见在虚拟储能控制框架内考虑电压支撑的必要性。图2 中的结果表明,基于分布式MPC 的虚拟储能电厂能够快速、紧密跟随电网控制中心给出的调度信号,参与电力系统有功平衡,为电网提供不同时间尺度的有功辅助服务；同时,配电网节点电压均控制在允许范围内,保证了可再生能源接入下配电网电压的安全与稳定。

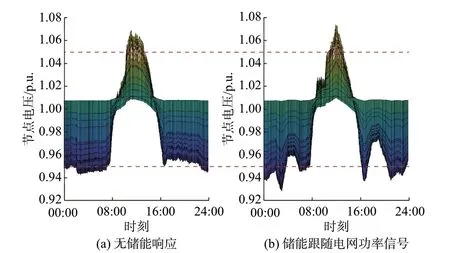
图1 无储能电压支持情况下IEEE 33 节点系统电压Fig.1 System voltage of IEEE 33-bus system without voltage support of energy storage

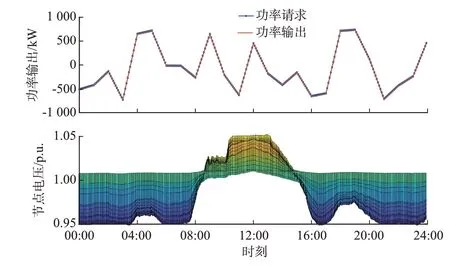
图2 算例1 中虚拟储能电厂功率与配电网节点电压Fig.2 Power of virtual energy storage plant and node voltages of distribution network in case 1

图3 给出了系统中所有分布式储能单元的充放电功率和SoC,可见储能单元出力与SoC 均满足设备物理限制；每个储能设备的充放电功率乘积保持为零,即未发生储能同时充放电的现象。

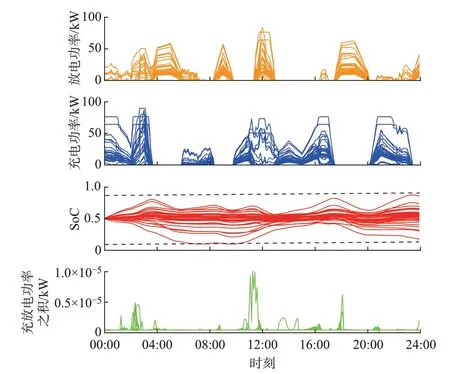
图3 算例1 中分布式储能单元的充、放电功率与SoCFig.3 Charging and discharging power and SoC of distributed energy storage units in case 1

图4 比较了集中式优化与分布式优化控制下虚拟储能电厂的运行成本,表明本文所提出的分布式优化控制方法能够给出与集中控制几乎相同的储能优化调度结果,即收敛到问题的最优解。但是,分布式优化方法中每个储能单元决策变量的维度为R2×H,相比于集中优化R2H×N的整体问题规模,显然算法需要搜索的变量空间更小。因此,每个控制周期内能用更短的时间给出最优的储能单元功率设定,且储能设备间的通信更为轻量化。

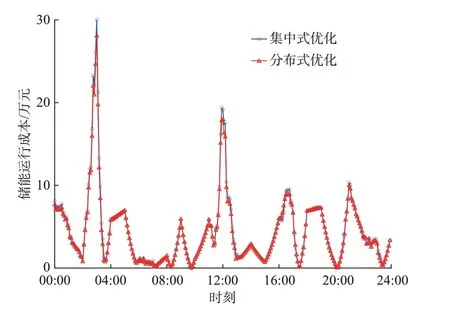
图4 集中式优化与分布式优化目标函数值比较Fig.4 Comparison of objective function values between centralized and distributed optimization

4.3 算例2

算例2 中的119 节点系统用于验证储能设备的大规模并网,系统参数参见文献［29］,该配电网系统额定电压为11 kV,总体的负荷水平为22 709.7 kW 和17 041.1 kvar。附 录A 图A4 展 示 了119 节点系统内虚拟储能电厂的功率跟随与电压控制效果,验证了所提出的虚拟储能电厂控制框架既能跟随聚合功率请求,又能防止配电网电压大范围变化。图A5给出了储能的输出功率与SoC,与算例1相同,储能的运行约束得到满足。根据图5 对一个控制周期内算法的收敛性进行了分析,可见对偶变量残差与目标函数残差较快收敛到较小值,功率跟踪误差也随之减小,在约150 次迭代后满足循环退出条件。

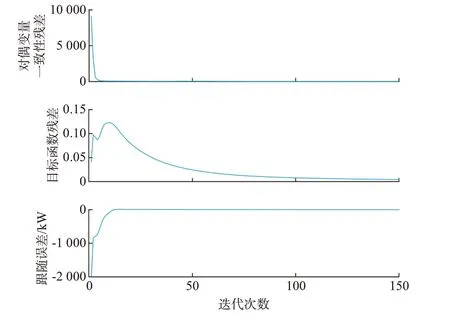
图5 单个控制周期内分布式优化算法的收敛性与功率跟踪效果Fig.5 Convergence and power tracking performance of distributed optimization method in one control step

附录A 图A6 纵向比较了仿真算例1 和算例2单个控制周期内集中优化与分布式优化方法的计算时间（忽略通信延时等因素）,其中分布式优化算法记录用时最长的储能智能体作为该步仿真的计算时间。从图中的结果可以看出,分布式优化方法依靠多智能体间的协同控制具有更少的计算时间,且在系统节点数明显增加的情况下体现出更好的扩展性能,能够快速调节聚合体输出功率以满足不同辅助服务要求。限于篇幅,本文并未讨论分布式储能系统的容量与布点配置,对于优化问题本身不存在可行解的情况将在以后的工作中开展研究。

5 结语

本文提出了虚拟储能电厂的分布式优化控制框架,给出了一种小容量分布式储能单元的聚合控制策略,使得储能设备集群具有与传统大规模储能相似的容量,并具有参与电网辅助服务的能力,验证了虚拟储能电厂不仅能够满足输电网等级的功率调控请求,还可为配电网提供局部电压支撑,有效提升了用户侧储能设备的应用水平。仿真算例验证了该方法在不同电网应用场景中的有效性。