货车轮对尺寸动态检测系统综合标定方法

丁 源,马宏伟,曲 辉

(1．国能铁路装备有限责任公司，北京 100048；2．天津哈威克科技有限公司，天津 301799)

1 引言

轮对尺寸是影响车辆行驶安全的重要因素之一，因此，相关部门对轮对参数测量有严格规定与要求[1]。传统人工轮对尺寸检测方法容易受到主观因素影响，不但增加劳动强度，还会降低检测效率[2]。利用计算机与图像技术的轮对尺寸检测是现阶段广泛使用的方法。而有效的标定过程则是确保尺寸检测精度的关键。

崔凌燕等人认为，摄像机标定是利用一组参数来表示已知机器视觉系统的成像过程，包括摄像机内外部参数。因此利用正方形标定模板对图像进行处理，结合直线特性约束条件与正方形性质计算摄像机畸变系数，再根据最小二乘法获取摄像机外部参数[3]。该方法只利用一个正方形轮廓即可实现标定，标定过程较为简便。

姚强等人利用亚像素边缘完成标定板特征提取，从而实现标定。首先对标定板图像进行采集并处理，得到像素级别边缘，将边缘像素点作为中心，取3×3的数字窗口运算梯度方向，并完成图像灰度的双曲正切拟合，从而获得级别边缘。最后按照圆形对像素边缘拟合，计算圆心坐标，实现标定[4]。该方法运算速度较快，还可应用于图像分割领域。

虽然上述两种方法能够在不同程度上提高标定精度，但容易受到作业环境影响，导致标定过程不稳定，因此适用性较低。为进一步改善标定性能，本文在平面方程的基础上，对货车轮对尺寸动态检测系统综合标定方法进行研究。在检测过程中，获取的原始图像效果通常不理想，因噪声、光线与拍摄角度等因素使图像质量降低，出现图像几何畸变现象。本文通过构建非线性畸变模型明确待检测图像的转换关系，可实现较为复杂的非线性处理，使标定过程具有灵活变通能力，从而进一步提高标定精度。

2 货车轮对尺寸动态检测系统结构与特点分析

对运行在铁路正线上的车轮尺寸进行动态检测，能够获得轮对重要技术指标。货车轮对尺寸动态检测系统通过分析对比所采集的参数，能够及时发现尺寸不满足要求的轮对，从而对故障轮对及时预警。系统组成结构主要包括轨边设备、探测器、列检作业场复示站以及管理中心终端设备等。

货车轮对尺寸动态检测系统具有如下特点：

(1)利用在线动态测量方法，不需要停车，不必对轮对进行拆分，因此检测速度较快、作业效率高；

(2)非接触性检测，不会对货车的正常运行造成影响；

(3)可实现全部自动化检测，可全天作业；

(4)能够自动完成数据采集和处理；

(5)可实现与其它设备的接口作业。

检测现场特殊的环境会对货车轮对尺寸动态检测系统中标定装置的使用产生一定的限定条件，主要有如下几点：

(1)货车轮对尺寸检测是在车辆快速行驶状态下完成的，所以检测设备不能影响货车的正常行驶；

(2)轮对在铁轨正上方刚性转动，所以摄像机只允许在轨道侧下方开展数据采集工作。因此，为获取清晰度较高的初始图像，必须保证光轴和光平面之间有足够大的夹角[5]；

(3)由于在轨道下方的枕木呈等距离排列，因此，检测设备只能摆放在枕木之间。在考虑设备安装位置时必须考虑枕木摆放这一因素。

3 基于平面方程系数的综合标定方法研究

3.1 摄像机标定图像下非线性畸变模型

在货车轮对尺寸动态检测系统中，摄像机图像发生的几何畸变属于非线性变换，需利用二元二次方程构建非线性畸变模型。

假设(u，v)表示校正前图像的相对坐标，使用多项式变形技术后，图像相对坐标(u，v)和经过校正后的图像坐标(x，y)之间存在如下转换关系：

上述公式中，a0-a5与b0-b5均为方程组待定系数。对上述两个公式进行综合分析，只要已知6个以上的空间坐标与图像坐标的相对关系，即可计算方程的全部待定系数，明确整个待检测图像转换关系。

3.2 摄像机标定中的坐标系转换

将CCD 摄像机看作一个小孔成像模型，此模型可通过成像变换表示。成像变换过程会涉及不同种类坐标之间的转换。而在轮对成像过程中，主要涉及到下述几种坐标系：

(1)世界坐标系

世界坐标系代表客观世界的绝对坐标，因此也称作客观坐标系[6]。该坐标系属于用户随机定义的三维空间坐标，一般情况下将被测目标与摄像机视为一个整体来分析坐标系。3D立体场景多采用此坐标系。

(2)摄像机坐标系

将摄像机作为中心的坐标系xyz，其光心是摄像机原点，z轴属于光轴，且z方向表示正方向。

(3)像平面坐标系

在摄像机内生成的像平面坐标系x'y'，用来代表像点在平面中的位置，一般结合坐标系x，y来确定。像平面平行于摄像机坐标系的xy平面，且x轴和x'轴、y轴和y'轴均发生重合，此时像平面位于摄像机光轴上。

(4)计算机图像坐标系统

在利用视觉系统测量轮对尺寸时，为方便像点与相对点空间位置的互相转换，图像坐标系通常设置在正向f 焦距处。此时，数字图像使用的坐标系为UV。由于数字图像最终存放在计算机内部的储存器中，因此，必须将平面坐标变换到计算机图像坐标系中。

在实际检测过程中，可以利用传感器传输几何参数，如焦距、光学中心以及空间关系等参数。明确世界坐标系和图像坐标系之间的联系与转换公式。根据传感器特性与原理[7]，选择成像点与空间原点位置。镜头投影中心位于成像平面前侧，但是为降低系统复杂度，本研究在模型中假设成像平面位于投影前端焦距f 处。

在不考虑镜头畸变的情况下，确定物空间坐标和计算机图像坐标的变换矩阵如下：

其中，Z代表物空间坐标和计算机图像坐标的变换矩阵，即摄像机理想变换矩阵模型。等式右侧的RT阵代表位姿变换，变换矩阵中每一行和每一列的元素中只有一个有效，其余元素都为0。通过T置换，可将转置矩阵中的行变成对应的列、列变成对应的行。

3.3 确定摄像机视场大小

检测系统内摄像机视场的大小需要结合被测轮对的尺寸确定，在确保检测精度符合要求前提下，通过目标运动范围来设计。视场大小与成像光敏面之间的几何关系取决于摄像机成像模型[8]。

摄像机成像光路图如图1所示。

图1中，假设AB表示被测物体，其高度表示为H。A、B代表物体AB的成像，高度是h。此成像系统物距与像距分别是u、v。若成像系统的放大倍数是β，则存在下述比例关系：

图1 摄像机成像光路图

结合高斯定义可获得下述表达式：

综合分析上述两个公式，能够获得物距、焦距以及放大倍率之间存在的关系：

摄像机物方视场大小取决于被测物体大小。通过计算获取轮对表面激光曲线长宽和磨损后的极限轮对半径。因此在视场设计时，需要确保被测轮对直径的表面曲线处于视场中心区域[9]。

3.4 摄像机焦距设计

为满足系统检测精度的需求，要确保任意0．1mm 大小物体所成的像在一个像元之内。结合光学放大倍率公式，对光敏面横向与纵向包含像元数量Nx、Ny进行计算：

其中，Lx、Ly分别代表光敏面横向长度和纵向长度。综合分析CCD摄像机成本尺寸等因素，在满足公式(7)和(8)的基础上，选择像素数与。若摄像机光敏面像元尺寸均为d，则有：

由此可将摄像机系统的焦距表示为下式：

3.5 综合标定的实现

3.5.1 成像模型

在理想光学系统中，成像模型能够简化为透镜成像，如图2所示。图2中，DD'表示物体AA'经过透镜所成的像，O代表光学中心，AO即为物体距离u，OD即为像距v，OC即可表示焦距f。

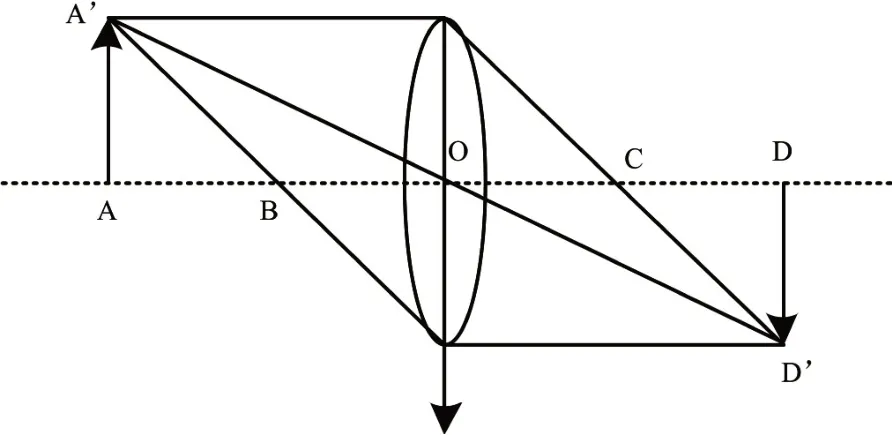
图2 理想透镜成像图

因此，在轮对尺寸动态检测系统中，假设OC表示摄像机光心，分析光学成像理论可知，与光轴Zc垂直的物平面中共轭平面的几何形状和物体完全一致，此相似比和放大倍率β相同。

结合高斯表达式可知[10]，物距倒数(1/u)与相距倒数(1/v)的和与焦距倒数(1/f)相等。因为在测量系统中，摄像机物距高于相距，所以像距v近似等于焦距f。因此在摄像机坐标系OC-XCYCZC中，可构建点AW的坐标(XAW，YAW，ZAW)和AC坐标(XAC，YAC，ZAC)的关系模型如下：

3.5.2 平面方程计算

假设AW，BW，CW三点相对的二维坐标分别为AC(XAC，YAC)，BC(XBC，YBC)与CC(XCC，YCC)。在坐标系OC-XCYCZC中，若AC点固定不变，BC，CC两个点在各自所在成像光线上运动，分别在△AWBWCW、△ACBCCC处停止，这时BC在处，CC在处，两点偏移量分别表示为DZB、DZC。此时与的坐标可分别描述为与。其中：

经过图像处理可以获得AC，BC，CC的坐标，则有：

根据上述公式可以获取DZB与DZC的相似比，从而得到物点AW的坐标。同理可得到高于三个特征点在此坐标下的位置后，即可拟合确定物平面在此坐标下的平面方程：

其中，P1-P4代表平面系数。

3.5.3 基于平面方程标定的实现

基于平面方程标定可通过公式(15)中平面系数P1-P4与坐标旋转矩阵R实现。假设在摄像机对点AW成像图中，表示摄像机平面，代表物平面，将OC当做摄像机光心，XW-YW-ZW属于以摄像机光心为原点的坐标系，同样的，X-Y代表图像坐标系，U-V代表像素坐标系。

若空间中随机一点AW在相机坐标系中的坐标表示为(XC，YC，ZC)，在标定板坐标是(X，Y)，与其相对的图像平面投影点像素坐标是(u，v)，图像坐标是(x，y)，此时相机内参数矩阵表示为：

公式(16)中，cxcy分别表示光敏面与光轴灯照在光敏面上位置的像素偏差值，通常为摄像机分辨率的二分之一。fx与fy分别为与单个像元相对的长宽。利用图像处理算法得到点AW对应的像素坐标，可根据如下表达式转换为相机坐标系下的坐标：

由于物点(XW，YW，ZW)、像点(xi，yi，f)以及光心OC(0，0，0)三点同在一条直线上，因此可确定如下方程：

物点处于所求标定平面上，对上述方程进行计算，可实现在摄像机坐标系下点AC与点AW坐标的转换。再利用最小二乘法获取旋转矩阵R，即可获取A点坐标在摄像机坐标系和世界坐标系之间的转换，过程如下述公式所示：

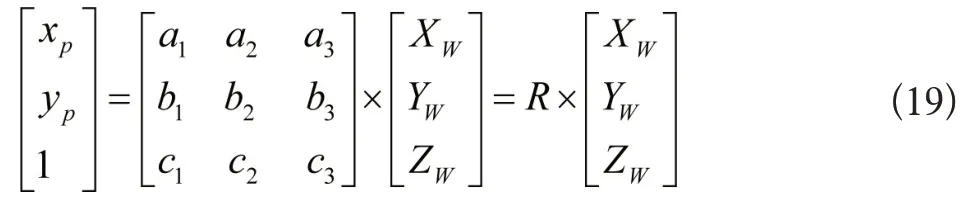
由此可知，与传统算法不同的是，所提算法没有利用拟合内参实现标定，而是通过拟合处理计算标定板平面系数P1-P4与旋转矩阵R来实现摄像机标定。

4 仿真实验与数据分析

为验证所提标定方法的应用性能，设计如下仿真实验。实验装置主要有：标定板、半导体激光源；摄像机、开关、采集卡等。被测目标平面范围大致为150mm×160mm，摄像机与被测目标距离为650mm。摄像机型号是MTV-1881EX，CCD 尺寸为7．5mm，像元数为654×476，半导体激光器波长是650nm，光条线宽低于1mm。

为了避免本次实验结果过于单一、缺乏对比性，将适用于轮廓检测和基于亚像素边缘中的标定方法作为对比方法，从标定精度与标定耗时两个角度对本文方法、适用于轮廓检测方法和基于亚像素边缘方法的应用性能加以检验。

首先检测不同方法的标定精度，结果如图3所示。

分析图3可知，随着实验次数的不断增加，不同标定方法的标定精度也随之发生变化。适用于轮廓检测和基于亚像素边缘方法的标定精度仅在最开始时高于本文方法，而后逐渐下降。本文方法的标定精度呈不断上升态势，最高的标定精度接近95%。

图3 不同方法标定精度对比

在此基础上，检测不同方法的标定过程耗时，结果如图4所示。

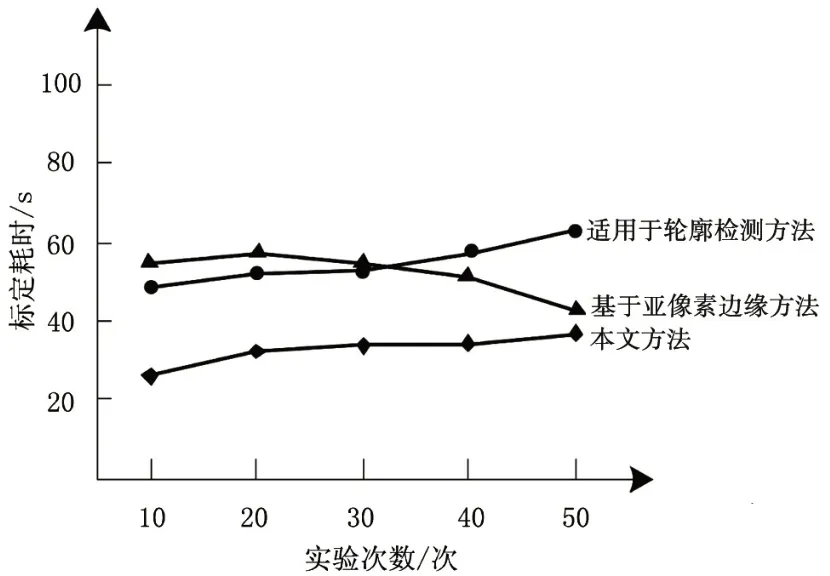
图4 不同方法标定耗时对比

分析图4可知，随着实验次数的不断增加，不同标定方法的标定耗时也随之发生变化。适用于轮廓检测和本文方法的标定过程耗时呈不断上升态势，而基于亚像素边缘方法的标定过程耗时先上升后下降。但相对来说，本文方法的标定过程耗时始终少于两种对比方法。

综上所述，本文方法能够在更短的时间内实现更精准的标定，这主要因为本文方法准确建立了图像非线性畸变模型，明确图像转换关系，从而提高标定精度和效率。

5 结束语

本文通过平面方程对货车轮对尺寸检测系统综合标定方法进行研究，并取得了良好的应用效果。

但在整个标定过程中，中间环节较多，每一个步骤都可能产生一定误差。虽然已取得了理想的标定精度，但在接下来的研究中，为进一步改善标定效果，还需对每个环节进行单独研究，例如在图像处理过程中减少信息量缺失等。