一种多医用配送机器人系统协同路径规划方法

董钰颖,杨雷恒

(西安航空职业技术学院 航空维修工程学院，陕西 西安 710089)

1 引言

新型冠状病毒爆发以来，大量医护人员奔赴一线开展疫情防控工作。但是在治疗病人的过程中，医护人员被传染的情况时有发生。利用移动机器人代替医护人员进入医院病房、手术室等区域完成物品配送工作，既能减少医护人员交叉感染的风险，又能够在一定程度上减轻医护人员繁重的工作负担。目前，世界上很多国家开始将移动机器人应用到医院环境中，并取得了一定的成果[1]。随着任务规模的不断增大，单一的机器人难以完成复杂任务，因此多机器人系统协同工作模式应运而生。较单一机器人而言，多机器人系统在环境自适应性、任务适用性、经济性、安全性及鲁棒性等多方面具有显著的优势[2-5]。多机器人系统协同路径规划问题的求解不仅仅是单机器人路径规划问题的简单叠加，还需要从全局的角度将不同任务分配给各辆机器人并规划出机器人执行各自任务的最优路径轨迹。

机器人在工作环境中的不同区域的移动过程可以看作是一个离散事件[6]，Petri网是一个针对离散事件系统典型的建模方法。Mahulea和Kloetzer[7]提出了一种基于Petri网的整数线性规划模型求解机器人最短路径的方法，将布尔逻辑描述的任务约束转化成一系列线性约束并整合成一个整数线性规划模型，通过模型求解计算出机器人的最优轨迹。马小军、芮峰等人[8]在文献[7]的基础上，通过着色Petri 网研究了不同种类的机器人在同一工作区域协同执行任务的路径规划问题。本文根据医院物品配送的实际需求，将配送任务的时效性、机器人最大载货量等限制因素考虑在内，提出了一种基于Petri网的多机器人系统协同路径规划方法。通过所提出的路径规划方法，能够有效快速地为每辆机器人获得符合任务需要的最优路径轨迹。

2 机器人工作环境建模与协同规划

2.1 Petri网基础

作为一种数形结合的系统描述和分析工具，Petri 网是一个四元组N=(P，T，F，W)，其中，P={p1，p2，…，pm}是m个库所的集合；T={t1，t2，…，tn}是n个变迁的集合[8]；F(P×T)(T×P)表示网结构中有向弧的集合；W：(P×T)(T×P)→N为Petri网的权函数；(N，M0)称为一个标识网，其中M0是Petri 网的初始标识；库所中的标识叫做托肯(token)，表示库所中的资源数量；令x PT，是Petri网中所有节点的集合。其中，前置集x，记作x={y PT|(y，x)F}，后置集x，记作x={y PT|(x，y)F} 。

Petri 网的几何结构能够通过关联矩阵C表示出来，它是一个n*m维的矩阵，其中，n表示网结构中有n个库所，m表示网结构中有m个变迁。其中，Pre：m*n→N，Post：m*n→N分别为PN的输入、输出函数矩阵，即Pre=W(p，t)，Post=W(t，p)，则有

Petri 网N 的某个标识状态M'是从初始状态M0触发一系列变迁∑={σ1，σ2，…，σh}产生的，即M0[∑＞M'。系统上述的运行关系可由包含初始状态的状态方程表示：

式(2)中的∑表示发射变迁序列的计数向量，即网系统每一次触发所发射变迁的集合。

2.2 工作环境建模

通过某医院实地调研可知，该医院的住院大楼一共有十层，其中一楼为综合治疗区域，二楼到十楼为专治科室，其中一层为一个科室，每个科室设有两个电梯间、一个护士站以及17个病房，每个病房中有4个床位供病人居住。医院设有草药、西药、颗粒药以及汤药四个药房，分别位于地下一层以及一楼大厅。由于住院部各科室内部环境布局类似，为了简化描述，以二楼内科科室和三楼骨科科室为例，将机器人工作区域模块化处理，介绍医院各功能区的位置分布情况，环境分布如图1所示。

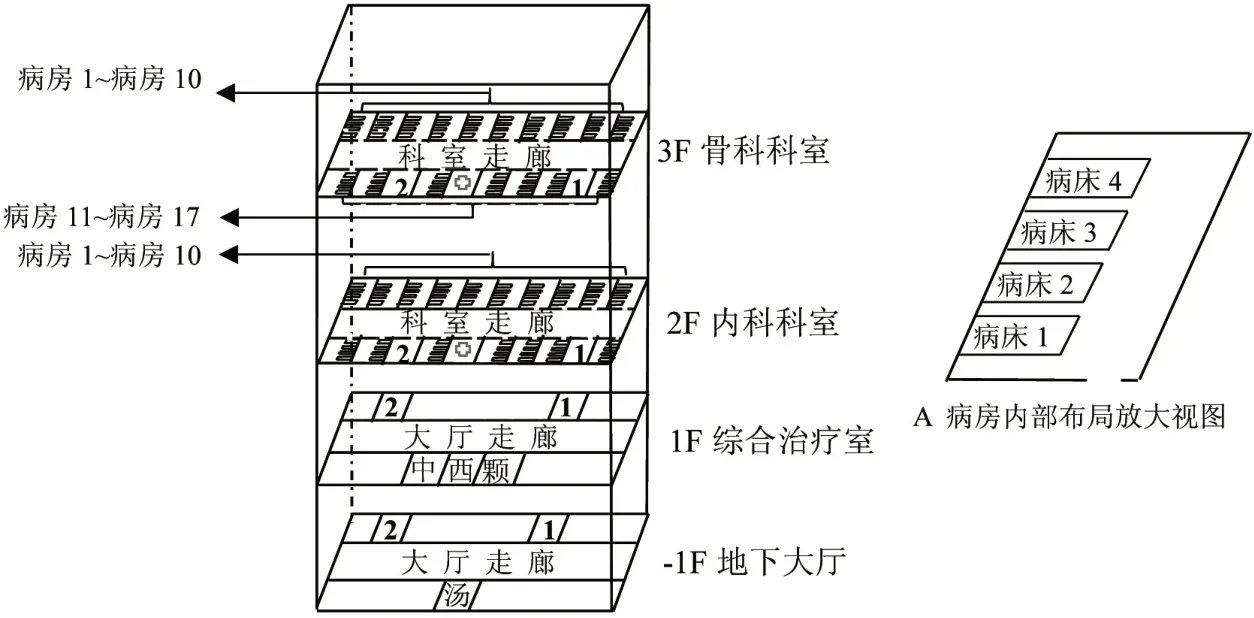
图1 医用配送机器人工作环境

根据图1所示的区域简图建立Petri网模型：按照药房、病房、护士站、电梯间等区域的位置分布，将内部走廊划分成若干小区域，其中每个小区域对应为一个库所；只有联通区域之间可以进行位移，区域的联通关系通过在两区域之间添加变迁表示，位移的过程可以通过触发变迁表示。由于医院是一个三维环境，机器人在执行任务过程中需要经过不同楼层，因此将机器人在不同楼层的移动过程通过触发连接在对应楼层电梯间的变迁实现。根据上述描述，建立Petri 网模型如图2所示，模型中一共有73个库所，162个变迁。其中红色区域为科室电梯间，蓝色区域为护士站，绿色区域为药房位置。

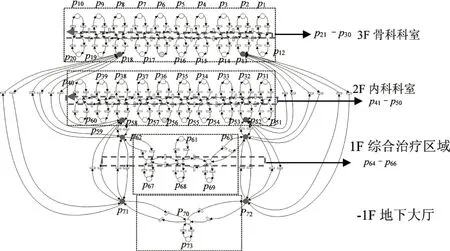
图2 医院工作环境的Petri网模型

为了实时监控机器人移动过程中距离、时间和载货量的变化情况，在相邻区域之间加权如下信息：

(1)di，j表示区域i到区域j的欧几里得距离，将距离信息di，j加权在对应的变迁上，表示机器人从区域pi移动到区域pj所增加的里程，通过对医院实际道路情况进行调研，加权对应变迁的距离信息具体如下：

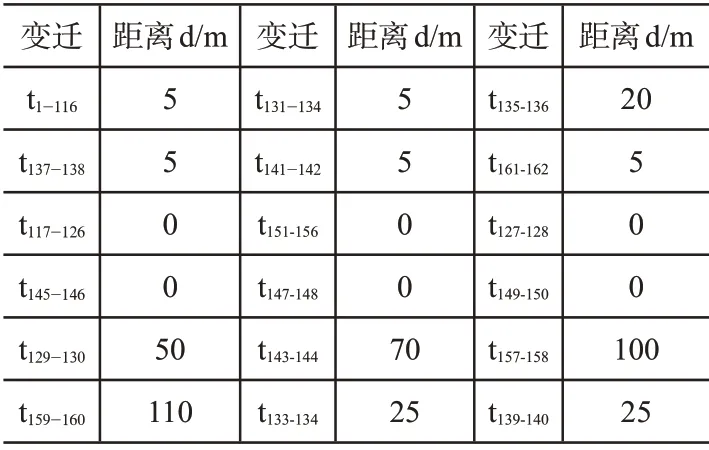
表1 医院环境中各小区域之间的距离信息

(2)bi，j表示机器人从区域i到区域j增加的载货量，即区域j对应任务的需求量qj，qj＞0 表示区域j为收货点，qj＜0 表示区域j为送货点，将区域j的需求量qj加权在对应库所pj的所有输入变迁ti，j上(i=1，2，…，73，i≠j)，表示机器人到任务区域j执行任务后增加的载货量；

(3)δi，j表示机器人从区域i移动到区域j需要的时间，将时间信息δi，j加权在对应变迁ti，j上，表示机器人从区域i移动到区域j的时间，机器人在相邻区域的通行时间根据道路实际距离、机器人行驶速度而定；

2.3 机器人系统协同路径规划任务描述

实际的物品配送工作十分繁重，需要多辆机器人协同完成。本文根据医院实际的环境情况以及物品配送的实际要求，将机器人的工作任务进行如下设定：

(1)每个配送任务都位于固定的区域，其中可能存在一些任务具有时间约束，需要对机器人系统进行任务分配，保证有机器人根据配送要求按时到达任务所在的区域才能完成配送任务；

(2)医院中存在一些禁止通行的区域，机器人们在执行各自任务的过程中需要避开这些区域。此外，机器人在执行完成各自任务之后需要就近回到规定休息区域补充电量，获得继续完成任务的能量；

3 基于Petri网的整数线性规划模型

3.1 基本假设

1)医用配送机器人型号一定，故额定速度一定，机器人总数量为K；

2)机器人工作环境是静态的、恒定的，各分区区域之间的距离已知，各道路始终处于畅通状态，机器人均按照额定速度进行工作；

3)在初始状态，系统中处于空闲状态机器人的位置已知；

4)工作环境中禁行区域位置已知，机器人补充电量的休息区域已知；

5)任务区域位置已知，需求量已知，需求时间窗约束已知；

6)假设所有配送机器人不存在技术方面的问题，执行任务前已储存足够的电量完成所分配的配送任务；

7)所有工作区域空间充足，允许多辆机器人同时经过同一区域；

8)一辆配送机器人可以为多个任务区域执行任务；

9)每个任务区域可以允许多辆机器人经过，但是只需要一辆机器人执行任务；

3.2 参变量定义

根据上述问题的描述和基本假设，现进行如下的变量和参数符号定义，如表2所示。

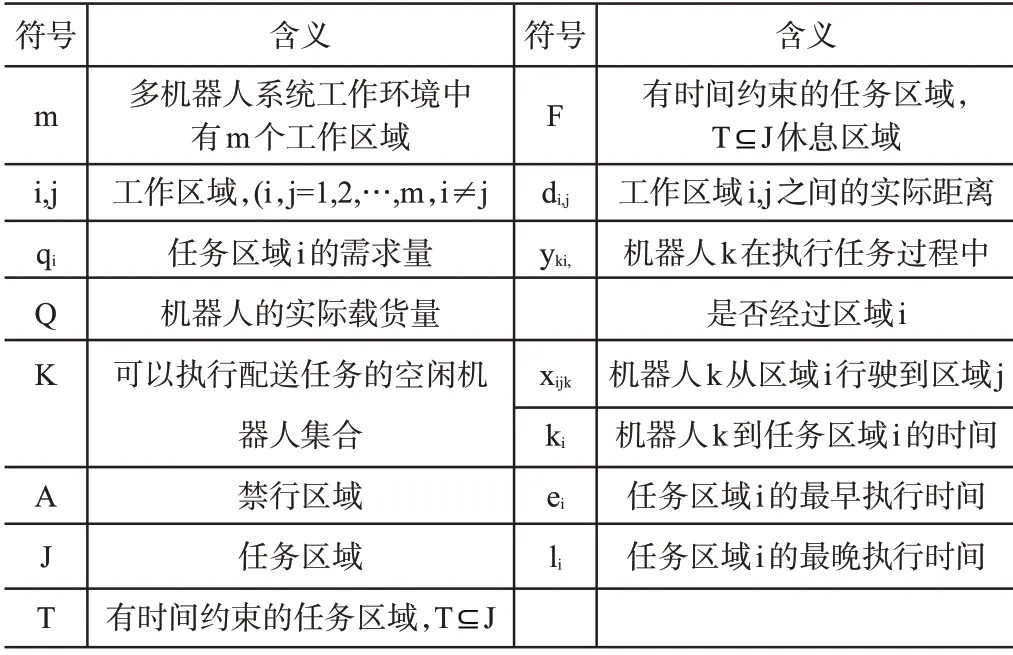
表2 符号含义

3.3 模型的建立过程

多机器人系统执行任务的过程可能存在前后顺序关系，由于实际的一些配送任务存在一定的时间约束，只有当机器人在规定的时间范围内到达对应任务区域执行任务才能认为该任务被完成。否则，就算有机器人到达任务区域执行相应任务但是没有在规定的时间范围内也会被认作任务执行无效。如何根据任务区域以及需求时间给每辆机器人提供执行任务的路径轨迹，保证机器人系统的总工作轨迹是满足任务要求最短路径轨迹。根据上述目标，建立如下路径规划模型。以多机器人系统总路径轨迹最短为目标函数：

式(2)为任务区域约束，即每个任务区域都需要至少一辆机器人到达并执行配送任务；

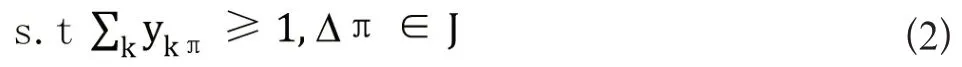
式(3)为禁行区域约束，即机器人们在执行任务过程中禁止经过禁行区域；

式(4)保证机器人们在完成全部任务后就近到休息区域补充电量，每个休息区域中可容纳至少一辆机器人补充电量；

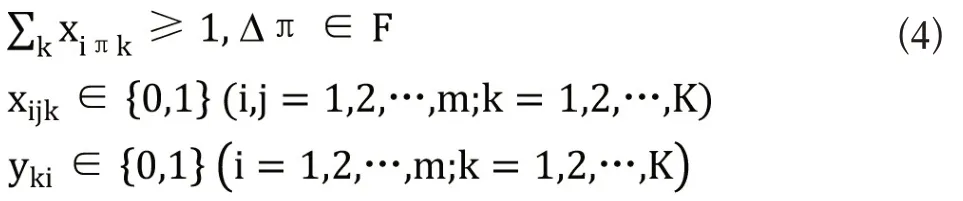
其中，引入0-1二值变量yki和xijk

4 实验结果

基于3．3节所建立的模型，在某医院实际环境对机器人系统进行仿真验证，某天上午七点，系统中有两辆空闲机器人停留在休息区域p64，此时系统接收到如下任务指令：

该任务描述为：机器人系统接受到任务指令后需立即派出空闲机器人从休息区域p64出发进行药物配送工作，机器人需要在[7：00，7：15]范围内到达颗粒药房p67、西药药房p68、中药药房p69、汤药药房p73中取药，其中颗粒药的取药量为两个单位、西药的取药量为五个单位、中药的取药量为八个单位、汤药的取药量为九个单位；取药完成后需要在[7：20，7：45]范围内到达病房p54、p34、p3、p4、p15、p64中为病人配送需要的药物，病房p54的需药量为十个单位，病房p34的需药量为五个单位，病房p3的需药量为三个单位，病房P4的需药量为四个单位，病房p15的需药量为两个单位；当机器人们完成所有的配送任务，必须返回休息区域p64中补充电量。机器人进行取药和送药的过程均在药房和科室医护人员的协助下进行药品的核对与分装。

通过Matlab 软件对所提出的模型进行仿真，计算出机器人们执行任务的路径轨迹，仿真结果如下：

机器人1 的路径轨迹：p64(0)→p65(2)→p66(2．5)→p69(3)→p66(8．5)→p65(9)→p68(9．5)→p65(15)→p63(15．1)→p67(15．6)→p63(20．1)→p61(21．1)→p52(26．1)→p42(28．4)→p43(28．46)→p44(28．52)→p34(28．82)→p44(31．12)→p54(31．42)→p44(33．72)→p43(33．78)→p42(33．84)→p52(34．14)→p61(39．14)→p63(40．14)→p65(40．24)→p64(42．24)

机器人2 的路径轨迹：p64(0)→p65(2)→p63(2．1)→p61(3．1)→p70(8．1)→p72(10．1)→p73(10．6)→p72(16．1)→p70(18．1)→p12(26．1)→p22(28．4)→p23(28．26)→p24(28．46)→p4(28．82)→p24(31．12)→p25(31．18)→p15(31．48)→p25(33．78)→p24(33．84)→p23(33．9)→p3(34．2)→p23(36．5)→p22(36．56)→p12(36．86)→p61(43．86)→p63(44．86)→p65(44．96)→p64(46．96)

如上可知，机器人们在任务规定的时间范围内到达任务区域进行配送服务，在机器人执行任务的过程中均未超过机器人的额定载货量。机器人们的总移动距离为750m。

5 结束语

根据医院当前物品配送任务繁重的现状，本文提出了一种对医院工作环境建立Petri 网模型的建模方法，并基于Petri 网特性提出一个整数线性规划方法，本方法能够对机器人进行合理的任务分配并规划出最优的路径轨迹。通过提出的模型能够保证机器人根据环境要求在不经过禁行区域的同时到达任务区域执行任务并最终回到休息区域，该方法通过MATLAB仿真获得了验证，根据仿真结果可知本文所提路径规划方法能够为多机器人系统规划出不碰撞的最短路径轨迹，同时保证所有的任务都能在规定时间范围内完成，证明本文提出的方法可行且计算效率高，能够有效解决医院目前急需解决的配送任务，为减轻医护人员的工作负担提供了一个有效的思路。