均匀磁化长方体的磁张量无解析奇点正演方法

邰振华， 柴 琳， 黄德智， 商宇航

(黑龙江科技大学 矿业工程学院， 哈尔滨 150022)

0 引 言

在基础地质研究、矿产勘查、工程与环境调查等领域，长方体是模拟磁性场源的重要模型，常用于基础转换、边界检测等数据处理方法的模型实验，是三维反演的核心构件[1]。用于模型实验时，长方体的正演值作为待处理数据，若存在解析奇点，可能导致实验效果不佳，如边界检测出现间断、虚假特征等。三维形态、物性反演需要将地下空间剖分成长方体单元，以其正演值与观测值的拟合度调控迭代进程[2]。然而，长方体正演结果的解析奇点恰好位于角点，导致迭代运算的收敛性差甚至无法收敛。

在常规磁异常的正演方面，郭志宏等[3]最早指出，长方体的常规理论表达式在上半无场源空间存在无法计算的解析奇点，推导了新的磁异常与梯度正演公式，降低了奇点影响，但增加了计算量。骆遥等[4]利用欧拉方程重新推导了长方体磁异常与梯度的无解析奇点理论表达式，简化了公式构造，优化了计算量。Luo等[5]推导了均匀磁化多面体的磁异常与梯度正演公式，可用于倾斜长方体的正演，但必须预先给定法线方向、用于坐标变换的9个旋转角度，增加了设计阶段的工作量。Kuang等[6]推导了适用于起伏地形的长方体磁异常无解析奇点正演公式。

相比于常规磁异常，磁张量的分辨率更高，能提供更丰富、精细的地质信息[7]。研发基于磁张量的数据处理新技术，突破地质体位置、形状、物性等反演的精度瓶颈，已成为磁法勘探的研究热点[8]。与常规磁异常类似，磁张量的数据处理方法测试、三维反演依赖长方体模型。因此，研究长方体磁张量无解析奇点正演公式，能够推动磁张量三维反演技术的发展。

在前人的研究基础上，笔者推导了直立长方体的磁张量无解析奇点正演公式，给出了简洁的坐标变换方法，建立了倾斜长方体的磁张量无解析奇点正演方法。利用模型实验，验证了正演结果的准确性，分析了地磁倾角、偏角对磁张量的影响。

1 有解析奇点的磁张量正演公式

在常规正演理论中，长方体磁场的x、y、z方向分量依次为Hax、Hay、Za。基于地磁场基本理论，分别对Hax、Hay、Za求取x、y、z方向的一阶偏导数，可以得到长方体的磁张量正演公式，即

(1)

(2)

(3)

(4)

(5)

(6)

ξi=(-1)ia-(x-x0) ，

ηj=(-1)jb-(y-y0)，

ζk=(-1)kc-(z-z0)，

式中：V——磁力位；

μ0——真空磁导率；

J——磁化强度；

ξi、ηj、ζk、Ri,j,k——距离关系。

L、M、N——总磁化强度的方向余弦；

(x0，y0，z0)——长方体中心点坐标；

(x，y，z)——计算点坐标；

a、b、c——长方体各边长的一半。

当计算点与长方体角点的垂直投影点重合时，ξ=0、η=0，式(1)、(2)、(4)存在分母为零的部分，计算结果趋于无穷大，形成了解析奇点。

2 无解析奇点的磁张量正演算法

2.1 直立长方体的无解析奇点正演公式

骆遥等[4]重新推导了直立长方体的Hax、Hay、Za正演公式。在此基础上，依据地磁场基本理论，分别推导Hax在x、y、z方向的一阶偏导数，可以导出直立长方体磁张量Vxx、Vxy、Vxz的无解析奇点正演公式，结合磁张量的等价互换性质，得出

(7)

(8)

(9)

同理，分别推导Hay在y和z方向一阶偏导数，Za在z方向一阶偏导数，得出

(10)

(11)

(12)

分析式(7)～(12)可知，不存在分母为零的情况，整个计算区域不存在解析奇点。同时，新推导的磁张量正演公式继承了骆遥等研究成果的简洁属性，计算量较小。

2.2 倾斜长方体的无解析奇点正演算法

对于走向与x、y方向不平行或者倾角不为90°、0°的倾斜长方体，磁张量正演可以借助坐标变换的方法加以实现。若长方体走向与x方向的夹角为α，则可以将原坐标系xyz围绕z轴逆时针旋转α角，形成新的坐标系xr1yr1zr1，如图1所示。

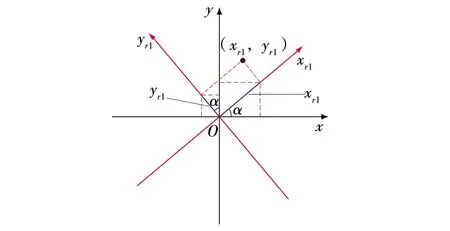
图1 围绕z轴旋转示意Fig. 1 Schematic of rotation around z-axis

xyz坐标与xr1yr1zr1坐标的变换关系为

(13)

将式(13)转化为矩阵关系式

(14)

同理，若长方体倾角不为90°、0 °，可以继续围绕x轴逆时针旋转β或围绕y轴逆时针旋转γ，建立新的坐标系。基于矩阵的乘法运算，最终的矩阵关系式为

(15)

(16)

在坐标系xryrzr下，倾斜长方体转化为直立长方体，ξi=(-1)ia-xr；ηj=(-1)jb-yr；ζk=(-1)kc-zr，可以利用式(7)～(12)计算磁张量正演值。而后，将坐标系xryrzr下的磁张量正演值转化回坐标系xyz，转化关系式为

(17)

式中：Vxx～Vzz——倾斜长方体在坐标系xyz下的磁张量正演结果；

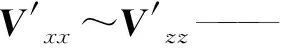
相比于Luo等[5]的坐标转换方法，文中方法只需给定与长方体产状直接相关的3个旋转角度，可有效降低模型设计阶段的工作量。

3 模型实验

3.1 直立长方体模型

为了检验直立长方体磁张量无解析奇点正演公式的正确性，设计如表1所示的单一直立长方体模型，其中，θ为地磁倾角，θD为地磁偏角，J为磁化强度。令z轴向下，观测面是z=0的平面，利用式(7)～(12)计算各方向的磁张量无解析奇点正演结果(图2)。图2中，磁张量分布特征符合长方体的异常变化情况，非对称分布(图2f的低值圈闭)主要源于地磁倾角与磁偏角的影响。利用式(1)、(2)、(4)计算出有解析奇点的Vxx、Vxy、Vyy(图3)。对比图2a～c与图3a～c，除4个解析奇点外，式(1)、(2)、(4)与式(7)、(8)、(10)的计算结果完全一致。此外，以表1模型产生的磁异常为基础，利用磁张量转换方法计算磁张量[9]，与无奇点正演结果的差异见表2。考虑到磁张量转换过程存在频谱畸变与转换误差[10]，张量转换与文中无奇点正演公式的计算结果基本相符。上述实验结果说明，文中推导的直立长方体磁张量无解析奇点正演公式是正确的。表2中均方差、均方差占比计算公式为

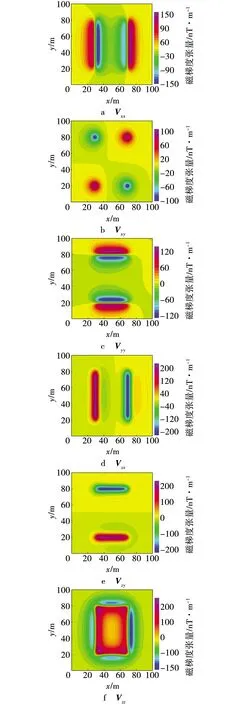
图2 直立长方体磁张量无解析奇点的正演结果Fig. 2 Forward results of upright cuboid magnetic tensor without analytical singularities

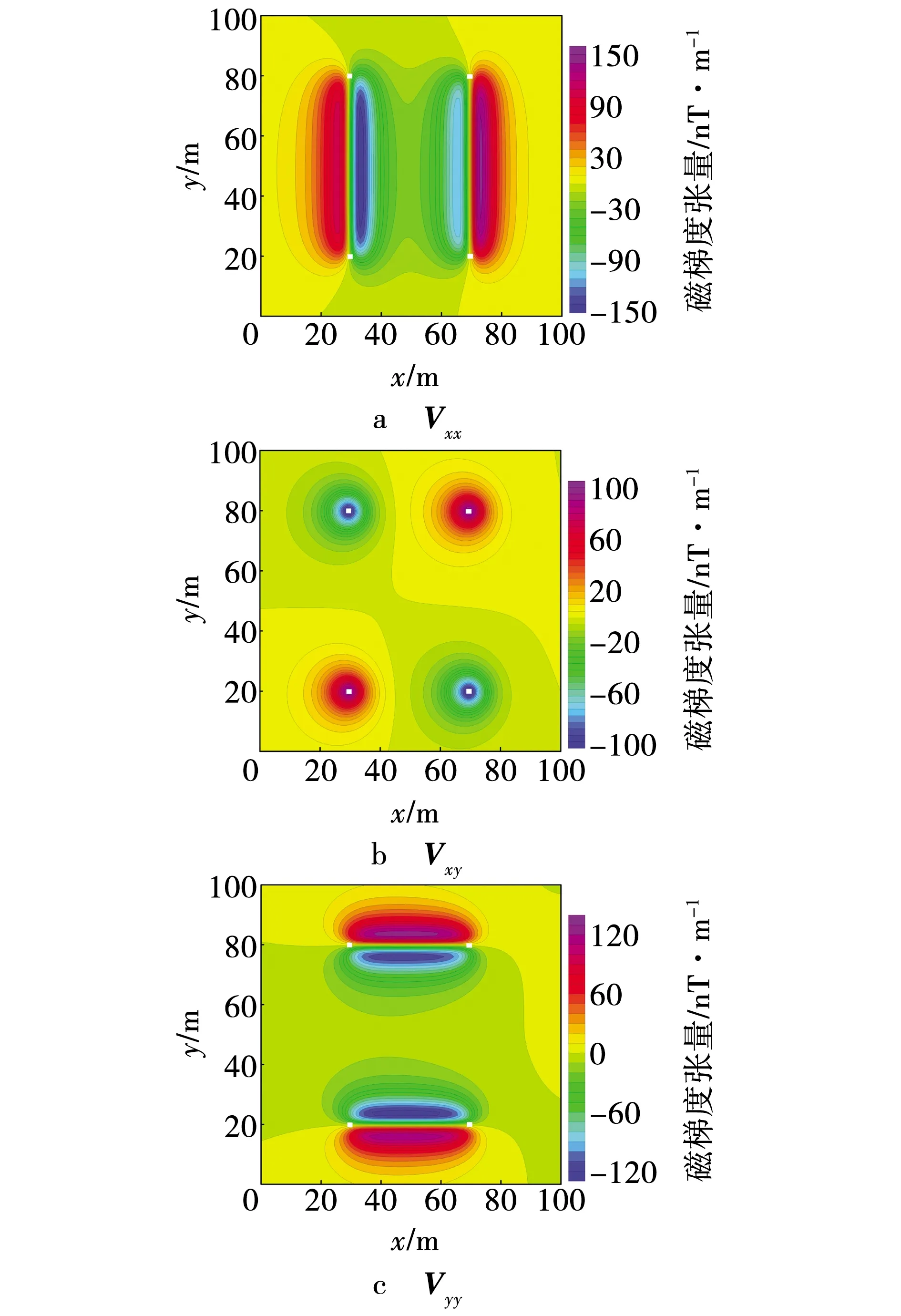
图3 直立长方体磁张量有解析奇点的正演结果Fig. 3 Forward results of upright cuboid magnetic tensors with analytical singularities

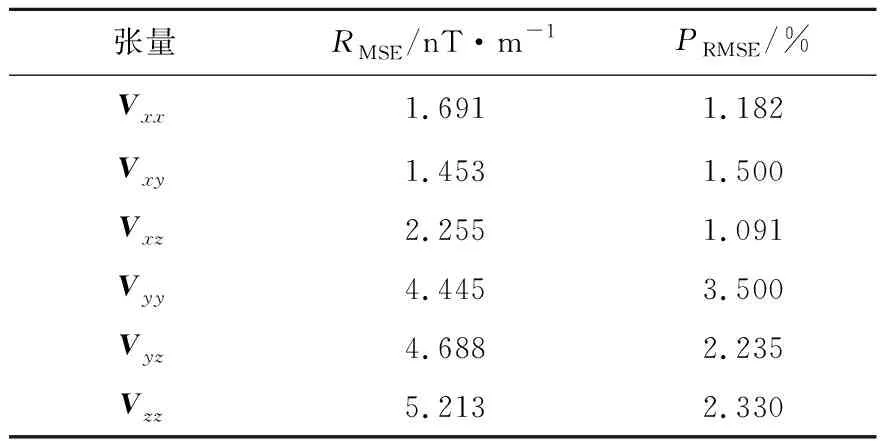
表2 斜磁化时无奇点正演结果与张量转换结果的误差Table 2 Errors between singularity-free forward results and tensor conversion results in inclined magnetization

(18)

(19)

式中：RMSE——均方差；

PRMSE——均方差占比；

FM——磁张量正演结果；

TC——磁张量转换结果；

|FM|max——FM绝对值的最大值；

K、J——x、y方向计算点总数。

3.2 地磁倾角与磁偏角的影响

依据表1，将地磁倾角改为90°、磁偏角改为0°，利用式(7)～(12)计算垂直磁化长方体的磁张量，与斜磁化正演结果(图2)的差值见图4。由图4可知，对于同一地质体，垂直磁化与斜磁化的磁张量差异较大，主要表现在张量的特征点(线)位置，如Vxx中的长方体边界位置、Vxy中的长方体角点位置。地磁倾角与磁偏角能够引起张量的幅值弱化、曲线形态变化，故化磁极同样是磁张量数据处理的必备环节。

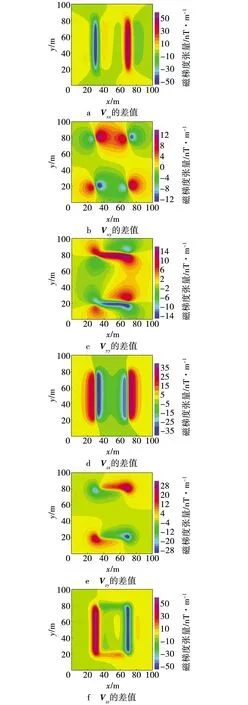
图4 斜磁化与垂直磁化的直立长方体磁张量差值Fig. 4 Differences between clino-magnetized and perpendicular-magnetized upright cuboid magnetic tensors

3.3 倾斜长方体模型

3.3.1 垂直磁化倾斜长方体模型

为了检验文中推导的倾斜长方体磁张量无解析奇点正演算法的正确性，设计如表3的单一倾斜长方体模型，θd为长方体倾角。令z轴向下，观测面是z=0的平面，分别利用张量转换方法与文中方法计算各方向的磁张量。分析图5可知，垂直磁化下，文中方法与张量转换方法计算的倾斜长方体磁张量差值很小，主要集中在磁张量变化较大的位置，与表4的误差统计相互印证。考虑到张量转换自身的误差，推导的倾斜长方体磁张量正演公式是正确的。

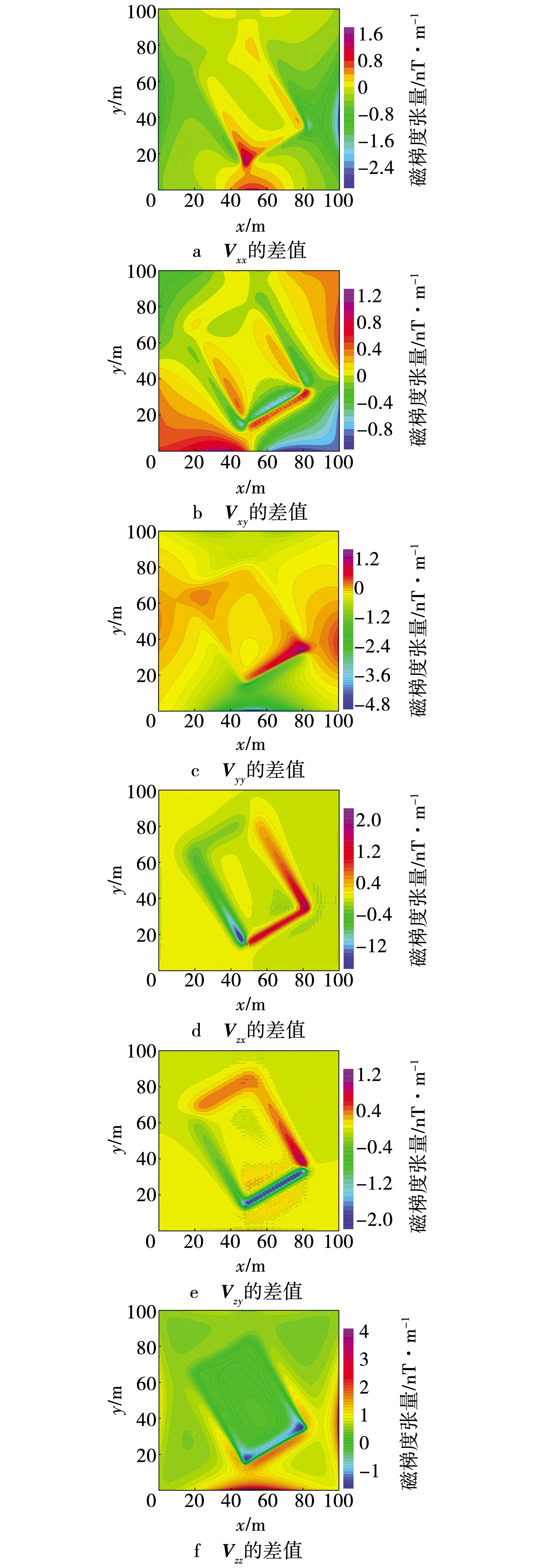
图5 张量转换与文中方法计算的倾斜长方体磁张量差值Fig. 5 Differences of inclined cuboid magnetic tensors calculated by tensor transformation method and this method

表3 倾斜长方体模型参数Table 3 Parameters of inclined cuboid model

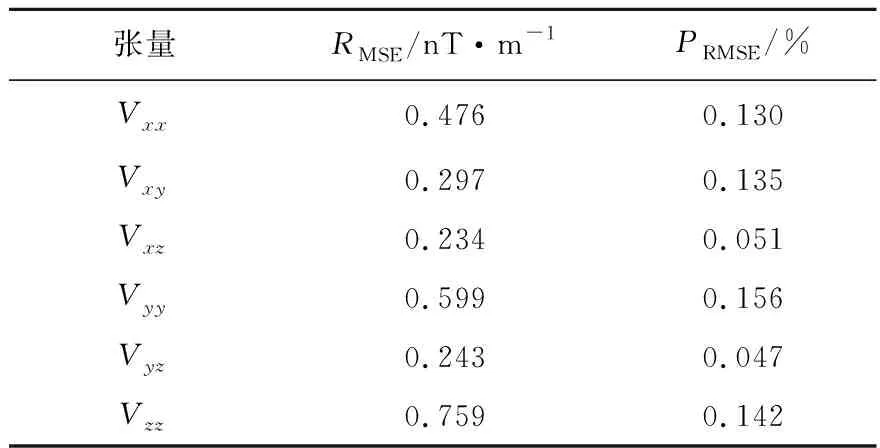
表4 垂直磁化时文中方法与张量转换计算的倾斜长方体磁张量差异Table 4 Differences of perpendicular-magnetized inclined cuboid magnetic tensors calculated by this method and tensor transformation method

3.3.2 斜磁化倾斜长方体模型

在不改变倾斜长方体参数(表3)的情况下，地磁倾角改为75°、磁偏角改为15°(斜磁化条件)，利用文中方法计算的磁张量如图6所示。与表3对比，磁张量正演结果的特征点(线)与长方体的角点(边界)对位，在张量Vxz、Vyz、Vzz中表现最明显；受地磁倾角与磁偏角影响，磁张量的极值圈闭呈现非对称的分布特征，轴线方向与地磁偏角对应。如表5所示，与张量转换方法的计算结果对比，PRMSE介于1.490%～2.990%。上述实验结果表明，文中方法计算的斜磁化倾斜长方体磁张量在等值线形态、幅值两方面均正确。表2与表5的对比结果说明，张量转换方法的计算精度同样受地磁倾角与磁偏角的影响，化磁极与张量转换的协同运算才能得到较好的转换结果。

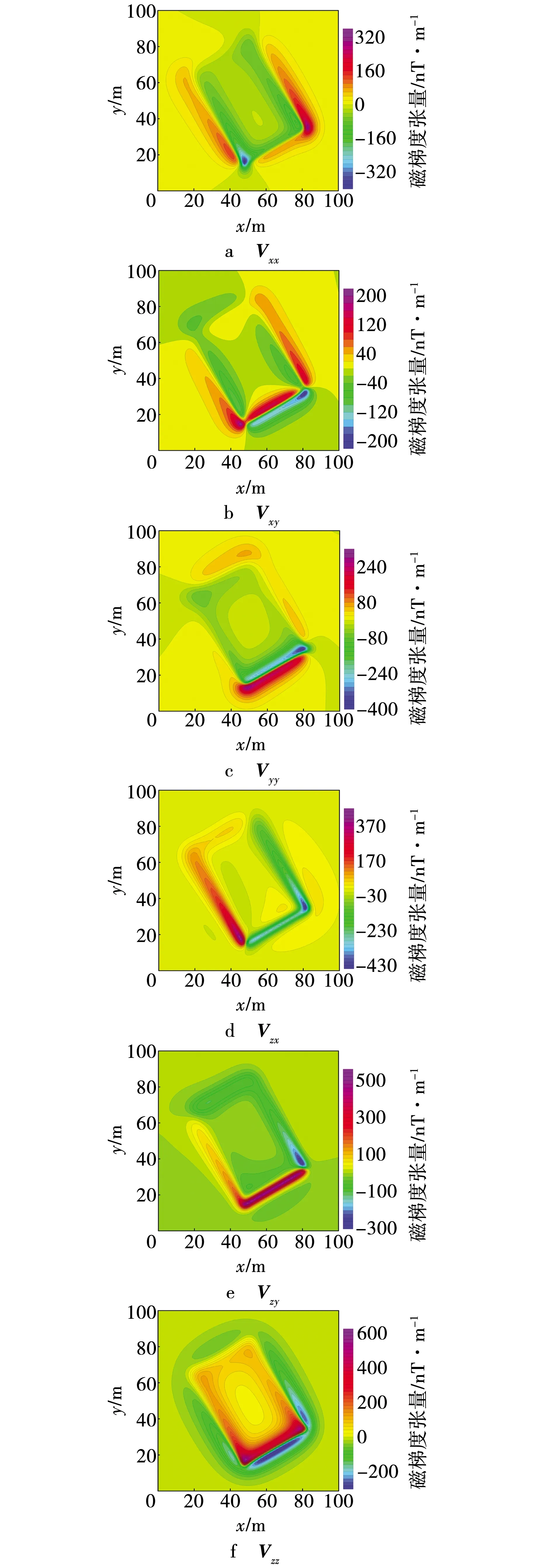
图6 文中方法计算的斜磁化倾斜长方体磁张量Fig. 6 Magnetic tensors of clino-magnetized inclined cuboid calculated by this method

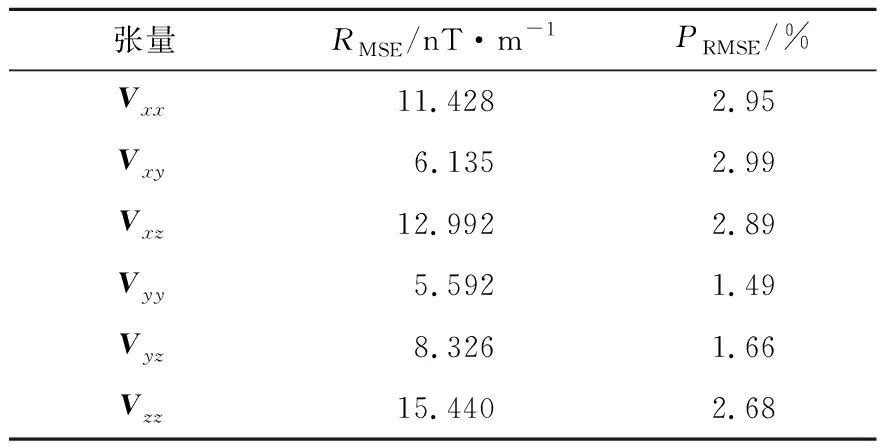
表5 斜磁化时文中方法与张量转换计算的倾斜长方体磁张量差异Table 5 Differences of clino-magnetized inclined cuboid magnetic tensors calculated by this method and tensor transformation method

4 结束语

在均匀磁化长方体磁场理论表达式的基础上，推导了直立长方体的磁张量有解析奇点与无解析奇点正演公式，建立了倾斜长方体的磁张量无解析奇点正演算法。实验结果表明，文中推导的磁张量无解析奇点正演算法是正确的；地磁倾角与磁偏角能够影响磁张量的幅值与分布，是降低张量转换精度的不利因素，故化磁极是磁张量数据精细化处理的必要环节。