支撑自复位能力对框架节点受力性能的影响

王 涛， 侯明珠， 孟丽岩， 钱 悦

(黑龙江科技大学 建筑工程学院， 哈尔滨 150022)

0 引 言

防屈曲支撑(Buckling-restrained brace，BRB)是近年来兴起的一种耗能装置，具有良好的耗能能力，可有效减小结构的最大变形，但震后会使结构产生残余变形，造成严重的经济损失和人身安全。自复位系统(Self-centering systems，SC)可以在很大程度上减小或者消除结构的残余变形，若将结合自复位结构和BRB，可以降低结构的残余变形和最大变形，将结构的地震反应降到最低。因此，具有可恢复功能的BRB已经成为抗震工程领域一个新的研究方向，受到了全球地震研究学者的青睐[1]。

2011年，Miller等[2]提出了形状记忆合金(Shape memory alloy，SMA)自复位防屈曲支撑(Self-centering buckling-restrained brace，SCBRB)，在BRB两端设置SMA棒提供恢复力，实验表明该支撑具有良好的耗能能力、延展性及有效的复位能力。2012年，刘璐等[3]提出了一种预应力钢绞线SCBRB，由预应力钢绞线来提供恢复力。2015年，王涛等[4]提出了一种弹簧式 SCBRB，复位系统由弹簧和方钢管串联组成。2016年，徐龙河[5]采用碟簧作为新型的复位材料，小变形位移下，碟簧拥有较大的承载力。2020年，钱悦[6]研究一种基于碟簧型的可更换SCBRB，解决了耗能系统难以更换的问题。SCBRB具有良好的耗能能力和变形能力，同时作用于结构中还可发挥其可恢复能力及复位能力，减小结构的残余变形，解决了BRB残余变形带来的不利影响[7]。 SCBRB紧跟社会的发展，满足可恢复抗震结构的要求，减小经济损失，为结构提供韧性能力。

在实际工程应用中，节点板作为连接支撑和框架的主要构件，节点板性能的好坏通常会与整个结构体系抗震性能密切相关[8]。节点板的破坏会导致节点连接处失去原有功能，引起整个框架结构脆性破坏，从而严重降低了结构抗震性能，节点板对整个结构体系尤为关键。赵俊贤等[9]提出了防屈曲支撑滑移连接节点的构造方式，有效减小了节点板的塑性损伤。笔者以自复位防屈曲支撑焊接框架节点为研究对象，对支撑复位系统进行参数分析，通过建立支撑框架节点有限元模型，调整系统复位率，以揭示支撑复位能力对框架节点的影响规律。

1 支撑复位系统的参数分析

SCBRB自身具有较好的耗能能力和变形能力，同时作用于结构中还可发挥其可恢复能力及复位能力。影响SCBRB复位能力的因素有复位率、强度比、屈服位移比等，其中，支撑复位能力主要通过系统复位率来控制。SC第一刚度由内、外管刚度共同控制，SC第二刚度由系统复位率α和BRB第二刚度共同确定[6]。

KS2=αKh2,

(1)

式中：KS2——复位系统第二刚度；

Kh2——耗能系统第二刚度。

支撑的复位能力通过残余变形来衡量，系统复位率对支撑复位能力起着决定作用。加载时，承载力主要由KS2和Kh2控制。卸载时，KS2和Kh2控制支撑的残余变形。为更好研究支撑复位程度对支撑框架结构受力性能的影响，令Kh2为定值。通过数值模拟的方法，分析支撑在支撑复位率α=0、α=0.5、α=1.0时，随着支撑残余变形的改变，支撑复位程度对支撑、节点板和梁柱的影响规律。

2 SCBRB子框架有限元建模

2.1 焊接节点板模型

文中以文献[10]中防屈曲支撑钢框架结构为研究对象，在BRB基础上增加复位系统，采用ABAQUS软件对L型子框架结构进行数值模拟，研究支撑复位能力对节点板塑性损伤的影响。SCBRB的简化模型通过BRB和SC并联实现，BRB采用桁架单元模拟，SC采用ConnSect连接器，其可以实现支撑复位功能。梁、柱、节点板采用实体单元建模，忽略耗能系统中内部构件的接触作用。梁、柱尺寸分别为2 825 mm×200 mm、4 825 mm×350 mm，节点板尺寸为426 mm×250 mm，节点板与梁柱焊接相连。SCBRB焊接节点板子框架有限元模型如图1所示。B点为水平滑动铰支座，C点固定，支撑仅对节点板提供支撑轴力，在E点输入水平位移荷载，加载位移的选取和输入将会在加载制度里进一步阐明。

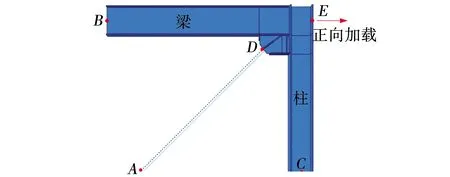
图1 SCBRB焊接节点板子框架有限元模型Fig. 1 Finite element model of SCBRB welded gusset plate subframe

2.2 材料本构模型

为更接近钢材实际弹塑性行为，采用Q235钢参数设置，对各构件截面赋予材料。梁、柱、节点板、BRB采用理想弹塑性模型，复位系统本构采用双折线模型。在ABAQUS复位系统双折线模型的复位系统预应力分别为-1 500、-450、0、450和1 500 kN，其所对应的复位系统的位移分别为-120、-1.2、0、1.2和120 mm；BRB弹性模量为206 Gpa，泊松比0.3，屈服力461.8 MPa，塑性应变0，截面面积2 338.7 mm2。文中框架节点采用与文献[10]相同的材料性能设计参数，梁、柱和节点板弹性模量均为206 GPa，泊松比为0.3，材料密度为7 850 kg/m3。

2.3 接触关系

接触关系选用面面接触，梁、柱和节点板相接触时，梁、柱内表面为主表面，节点板外表面为从表面。梁和柱相接触时，梁内表面为主表面，柱外表面为从表面。切向选用罚函数，法向硬接触，摩擦系数μ=0.3。

2.4 边界条件及约束关系

对梁底、柱底、荷载作用处、SCBRB与节点板连接处采用耦合约束。为模拟真实梁、柱和节点板的焊接约束关系，采用绑定约束，相当于焊接。BRB系统和SC系统相并联，采用MPC绑定形成SCBRB；SCBRB和节点板之间采用MPC栓约束。对于模型边界约束，框架仅设置平面内转动自由度。把支撑简化为二力杆，取桁架单元结构，故A点约束3个平动自由度，B点为滑动铰支座，C点为固定端，支撑与节点板铰接连接，D点约束3个方向的平动自由度。

2.5 加载制度与网格划分

多遇地震下，高层钢结构弹性和弹塑性层间位移角θ限值分别为1/250、1/50，加载时从1/250逐级递增。罕遇地震下，高层钢结构弹性θ限值为1/25。θ共取9个幅值，分别为1/250、1/200、1/100、1/67、1/50、1/40、1/33、1/29、1/25，每级幅值仅循环一圈，加载制度如图2所示。

图2 加载制度Fig. 2 Loading system

梁、柱网格尺寸分别采用30 mm×30 mm、50 mm×50 mm，厚度均为1层，梁板与柱体的连接为绑定连接；节点板网格取6 mm×6 mm，厚度为3层，节点板与梁柱焊接相连，焊缝横截面为12 mm2的等边三角形，横向长度为752 mm，纵向长度为200 mm。SCBRB为桁架单元，无需对其进行网格划分。模型网格尺寸划分见图3。

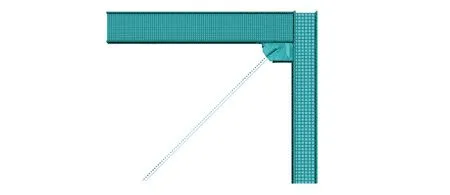
图3 模型的网格划分Fig. 3 Mesh generation of model

3 SCBRB焊接框架节点的复位能力

3.1 支撑的力学性能

支撑滞回曲线分析，层间位移角为1/50时，不同支撑复位率的支撑滞回曲线，如图4所示，当α=0时，复位系统不发挥作用，此时支撑相当于BRB，初始加载时，BRB滞回曲线呈线性上升，刚度幅值变化甚微。随着外力卸载，处于弹性变形阶段，滞回环无明显变化。当荷载持续增大，支撑进入塑性阶段，结构开始出现残余变形，刚度呈线性下降阶段，残余变形随卸载载荷的增加而增大。随着支撑复位率的增加，复位系统开始逐渐工作，当α=0.5时，复位系统第二刚度增大，卸载提前，随着支撑复位率的逐渐增大，滞回曲线的变化由“梭型”逐渐向“旗帜型”过渡。当α=1.0时，初始时屈服位移小，刚度大，很快从弹性过程进入塑性阶段，支撑滞回曲线为“旗型”，耗能能力稍微减弱。

支撑复位性能分析。由图4可知，随着α的增加，残余变形逐渐减小，复位能力增强。当α=0时，残余变形达到最大值80 mm，复位系统不发挥作用，此时支撑相当于BRB,结构最大层间位移角为1/60。当复位系统开始工作，α=0.5时，在卸载阶段，支撑呈线性下降，此时残余变形为40 mm，结构最大层间位移角为1/121；当α=1.0时，支撑承载力增大到3 000 kN时开始卸载，此时残余变形2 mm，结构最大层间位移角为1/2413，支撑基本实现完全复位。由此可见，随着支撑复位率的增加，支撑的复位能力在不断增大，残余变形由80 mm逐渐减小至2 mm，支撑复位率对复位能力影响较为明显。

支撑最大轴力分析。由图4可知，当α=0时，在加载阶段，只有耗能系统工作，此时支撑为BRB，支撑最大承载力为1 100 kN，耗能系统不发挥作用。随着支撑复位率的增大，支撑复位能力逐渐增强，当α=0.5时，继续加载，承载力逐渐增大到2 500 kN。当α=1.0时，支撑基本实现完全复位，持续加载，承载力增大到3 200 kN。在α=0和α=0.5区间内，支撑承载力增加幅度较大，最大承载力提高了1.27倍。在α=0.5和α=1.0这个阶段内，支撑承载力增加幅度减慢，最大承载力仅提高了28 %。由此可知，随着支撑复位率的增加，对支撑最大承载影响较大。在α≤0.5前支撑承载力迅速增大，在0.5≤α≤1.0时支撑最大承载力增长逐渐缓慢。

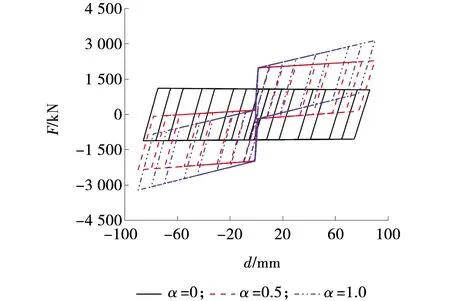
图4 不同支撑复位率的支撑滞回曲线 Fig. 4 Brace hysteretic curve with different brace stiffness ratio

3.2 子框架的力学性能

由子框架的应力云图，如图5所示，当支撑复位率α=0时，此时支撑相当于BRB，支撑无复位能力，柱上翼缘处开始出现弹性变形，梁柱翼缘相交处出现了应力最大值，为324 MPa。随着支撑复位率的增加，复位系统开始启动，当α=0.5时，支撑对子框架作用的轴力逐渐增大，柱端塑性变形范围缩小，应力增大，变形逐渐集中到梁柱交接点上方，此时应力最大值为389 MPa。梁端塑性损伤逐渐减小，塑性发展程度逐渐降低。当α=1.0时，随着支撑轴力的增大，柱端塑性损伤增大，塑性损伤范围也由梁柱上端交界处逐渐向周围扩大，其中柱端塑性损伤扩大较为明显，应力最大值为428.4 MPa。随着支撑复位率的增加，在0≤α≤0.5范围内，柱翼缘塑性铰逐渐上移，随着支撑轴力的增大，应力增加了65 MPa, 框架塑性损伤提高了20.06 %。在0.5≤α≤1.0范围内，梁柱节点处塑性损伤增大，范围也向梁柱翼缘扩散，塑性损伤主要向柱翼缘处扩散，此时应力增大至39.4 MPa，框架塑性损伤增大了10.13 %。框架承担的剪力主要集中在梁柱节点，有利于控制在荷载下梁柱翼缘的面外变形，减小SCBRB轴向变形及其累积塑性耗能的损失。

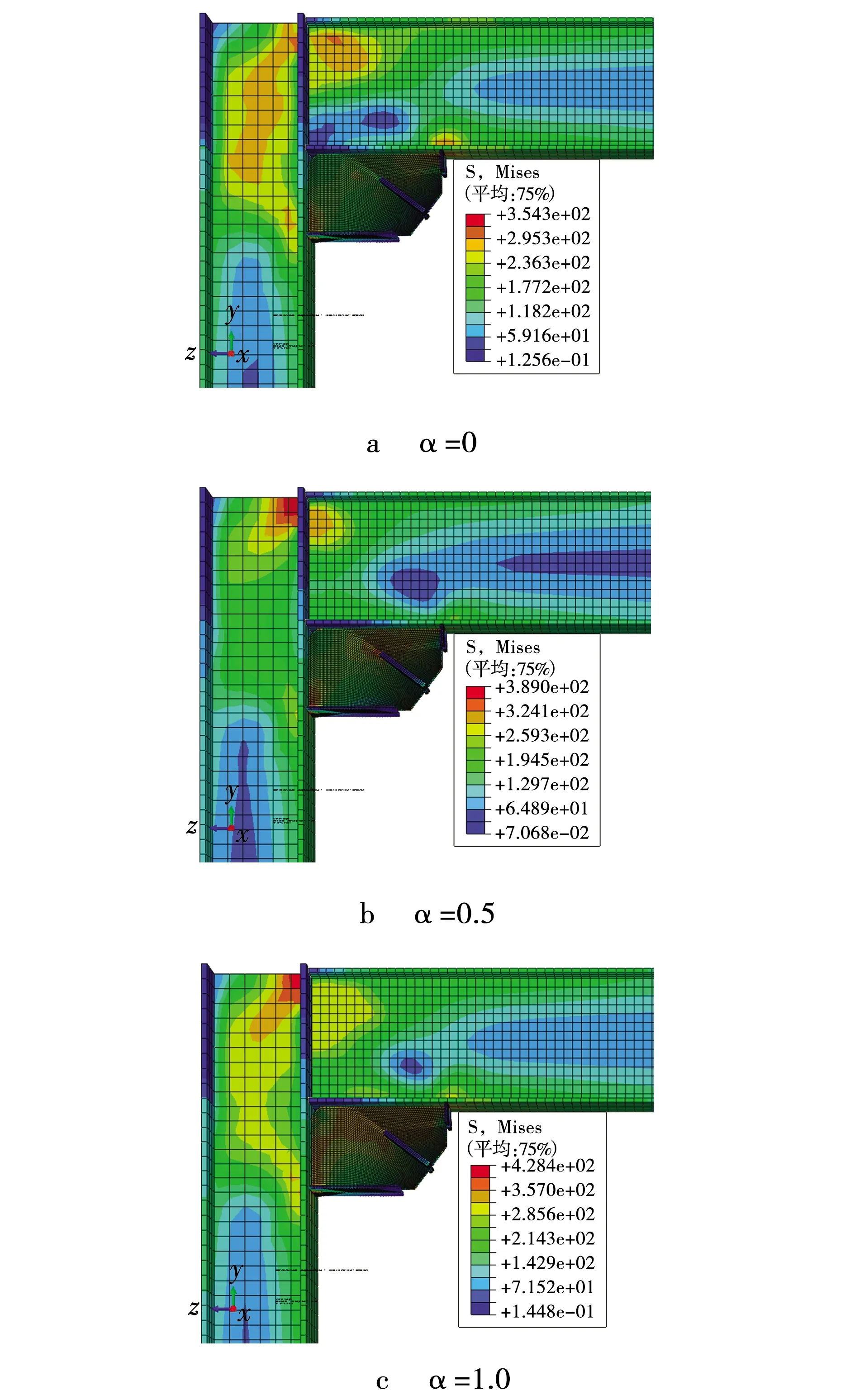
图5 不同支撑复位率的框架节点应力云图Fig. 5 Stress nephogram of frame connections with different brace stiffness ratios

3.3 节点板的力学性能

结构层间位移角为1/50时，不同支撑复位率的节点板应力云图如图6所示。当α=0时，此时支撑耗能系统发挥作用，支撑复位系统不工作，节点板应力最大值分别出现在与梁柱翼缘相交处的右上端与左下端，应力最大值345 MPa，节点板其它地方应力分布相对均匀。随着支撑复位率的增大，复位系统启动，支撑对节点板作用力增大，当α=0.5时，节点板塑性损伤已逐渐扩散至支撑与节点板相交处，节点板应力最大值为373 MPa。进一步增大支撑复位率，节点板塑性损伤逐渐下移扩大，应力损伤分布较为均匀，应力最大值388 MPa。随着支撑复位能力的增加，支撑对节点板的作用轴力加强。在0≤α≤0.5范围内，节点板应力变化较为明显，应力增加了8.12 %，节点板塑性损伤转移至支撑与节点板相交处。在0.5≤α≤1.0范围内，节点板应力呈上升趋势，变化幅度较为缓慢，这个阶段应力增加了4.02 %。

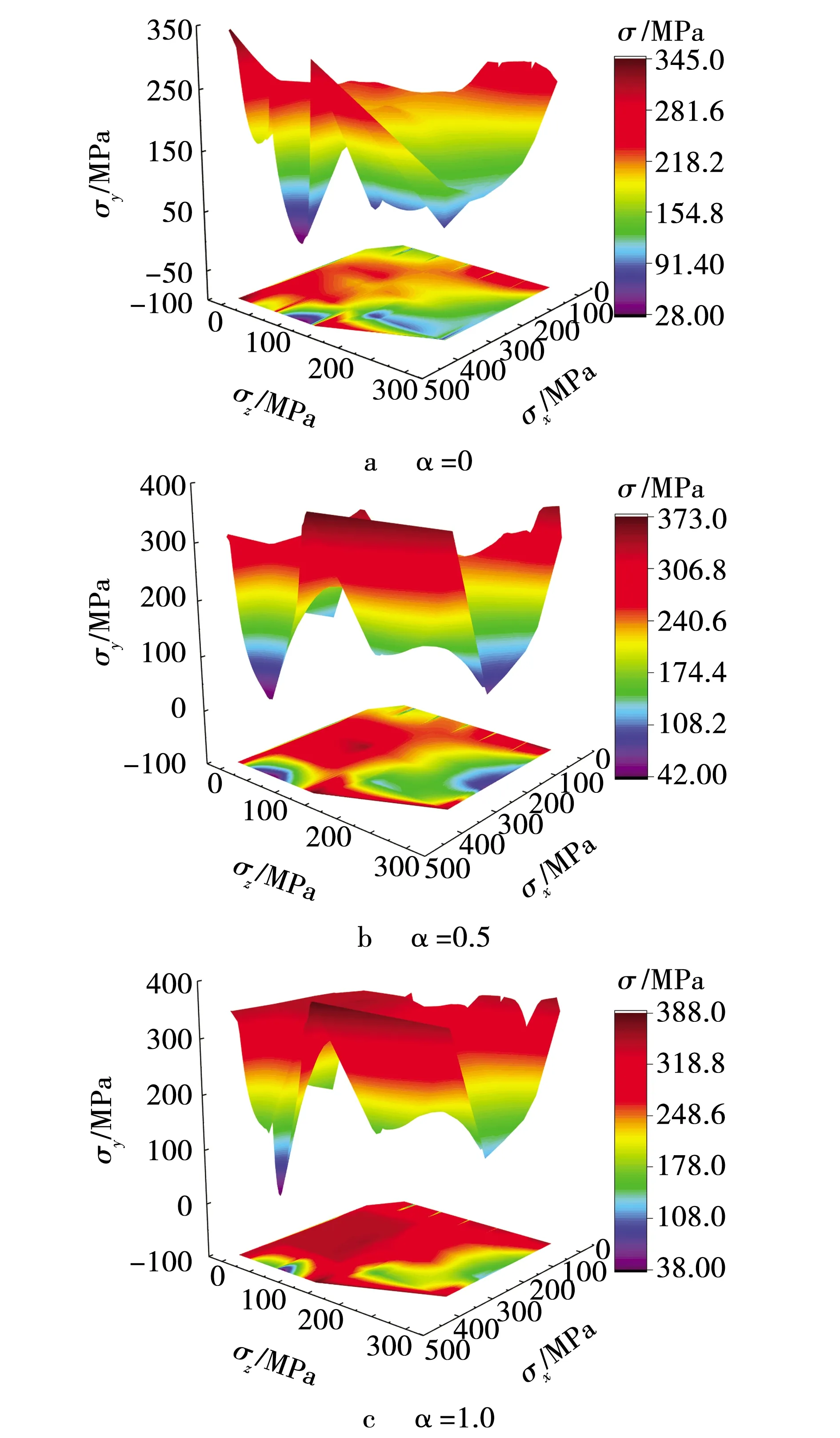
图6 不同支撑复位率的节点板应力云图Fig. 6 Stress nephogram of gusset plate with different brace stiffness ratio

4 结 论

通过调整支撑系统复位率分析了支撑复位程度对支撑、节点板和梁柱的受力性能，给出支撑复位能力对框架节点的影响规律。

(1)SCBRB与框架节点板相连时，随着复位率的增加，支撑残余变形减小，在0≤α≤0.5范围内，结构最大层间位移角由1/60逐渐减小至1/121，在0.5≤α≤1.0范围内，结构最大层间位移角由1/121逐渐减小至1/2 413，支撑复位能力得以发挥，结构抗震性能增加。

(2)随着复位率的增加，在0≤α≤0.5范围内，柱翼缘塑性铰逐渐上移，随着支撑轴力的增大，框架塑性损伤提高了20.06%。在0.5≤α≤1.0范围内，梁柱节点处塑性损伤增大，范围也向梁柱翼缘扩散，塑性损伤主要向柱翼缘处扩散，此时，框架塑性损伤增大了10.13%，梁柱节点处塑性损伤增大。

(3)随着复位能力的增加，在0≤α≤0.5范围内，节点板应力变化较为明显，应力增加了8.12%，节点板塑性损伤转移至支撑与节点板相交处。在0.5≤α≤1.0范围内，节点板应力呈上升趋势，变化幅度较为缓慢，该阶段应力增加了4.02%。复位系统屈服后表现出刚度增大的特点，节点板应力变化显著，其应力先迅速增大，后又缓慢增加，总体呈上升趋势。