砖混类建筑垃圾-粉煤灰充填材料配比的优化

陈维新， 张国华， 毕业武， 金珠鹏， 李 涛,4， 侯宪港

(1.黑龙江科技大学 矿业工程学院， 哈尔滨 150022; 2.黑龙江科技大学, 哈尔滨 150022； 3.黑龙江科技大学 安全工程学院， 哈尔滨 150022; 4.中国矿业大学(北京) 能源与矿业学院， 北京 100083)

0 引 言

目前我国充填开采主要采用矸石、膏体、高水、超高水、高浓度胶结料等充填材料，而充填原材料成本过高、来源不足是制约充填开采大面积推广的关键因素[1-5]。

随着城建进程的加快，我国建筑垃圾量已占城市垃圾总量的30%～40%[6-7]，2012年以来，我国新增建筑垃圾量均在10 亿t/a以上，新增量巨大，但其利用率偏低，不超过10%[8-9]。尤其是矿区电厂产出的粉煤灰，因市场需求量少而被排出废弃[10]。

近年来，学者们对废弃粉煤灰及建筑垃圾再生骨料用于充填材料进行了相关研究。刘音等[11]以建筑垃圾为骨料、粗粉煤灰基为胶结材料，采用正交实验分析了各因素对充填膏体性能指标的影响，确定了建筑垃圾膏体充填材料最佳配比。张保良等[12]模拟了膏体充填材料的配比实验和管道输送实验，分析了建筑垃圾-粉煤灰膏体充填材料的基本性能和流变特性。姜明阳等[13]采用正交实验确定了以建筑垃圾、天然砂、水泥和粉煤灰为组成材料的膏体充填材料最优配合比。仇文超等[14]分析了不同基料粒径对建筑垃圾基浆体膨胀充填材料强度的影响。李浩等[15]采用正交实验确定了建筑垃圾充填材料的最优配比，分析了建筑垃圾骨料-粗粉煤灰基胶结料充填体的力学性能。

虽然目前对建筑垃圾-粉煤灰胶结充填材料有了大量研究，但是针对某一具体种类的建筑垃圾作为充填材料骨料的研究还鲜有报道。因此，笔者尝试将砖混类建筑垃圾作为再生骨料，废弃粉煤灰作为主要细集料，制备高浓度胶结充填材料，拟通过正交实验建立回归模型优化充填材料配合比，分析充填材料工业配比的力学特性，得到相应结论。

1 原材料

1.1 建筑垃圾

对现场建筑垃圾进行分拣、3级破碎后得到再生骨料，主要由混凝土、砖块、砂浆、瓷砖等组成，吸水率为10.1%，将其筛分为0～0.075、0.075～2.5、2.5～5、5～10、10～16 mm这5个粒度区间，如图1所示。标准JGJ52—2006《普通混凝土用砂石质量及检验方法标准》中规定，粒径<0.075 mm的颗粒称为“泥”[16]。根据标准，该再生骨料中小于0.075 mm的粒径，即“泥”占再生骨料质量的8%。

图1 再生骨料加工过程Fig. 1 Processing process of recycled aggregate

Talbol级配理论认为，样本中粒径小于或等于d的质量占总质量的百分率满足以下方程，即

P=100(d/dmax)n，

式中：P——粒径小于d的再生骨料质量占试样总质量的百分比，%；

d——再生骨料粒径，mm；

dmax——再生骨料的最大粒径，mm；

n——Talbol级配指数。

对再生骨料的粒级分布η1按照Talbol表达式进行拟合，如图2所示。拟合曲线的复相关系数R2为0.98。该再生骨料的Talbol级配指数n=0.67。当n=0.30～0.60时，骨料堆积密度较佳，级配更加合理[17]。因此，该再生骨料级配大粒径较多，不在合理范围内。

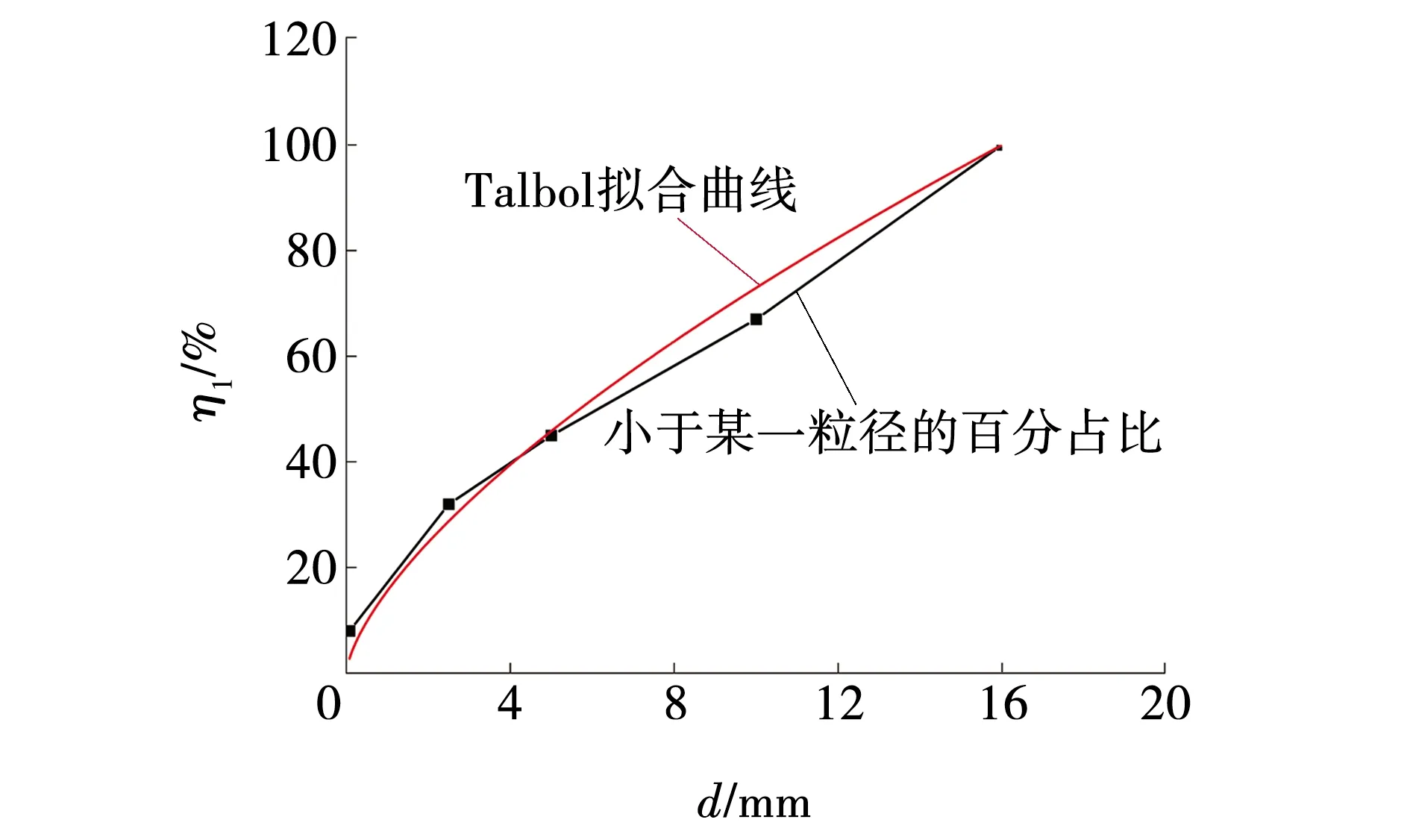
图2 再生骨料粒径分布曲线 Fig. 2 Particle size distribution curves of reclaimed aggregate

1.2 粉煤灰

图3为鸡西矸石电厂湿排废弃粉煤灰，平均含水率为4.2%。烘干后，利用激光粒度仪测其粒径分布，如图4所示。其中，η2为粉煤灰粒级负累计分布。该粉煤灰中间粒径占比过多，无法拟合为Talbol连续级配方程。计算粉煤灰的不均匀系数Cu=d60/d10=1.25，远小于5，说明其级配不良。

图3 现场废弃粉煤灰Fig. 3 Appearance of construction waste

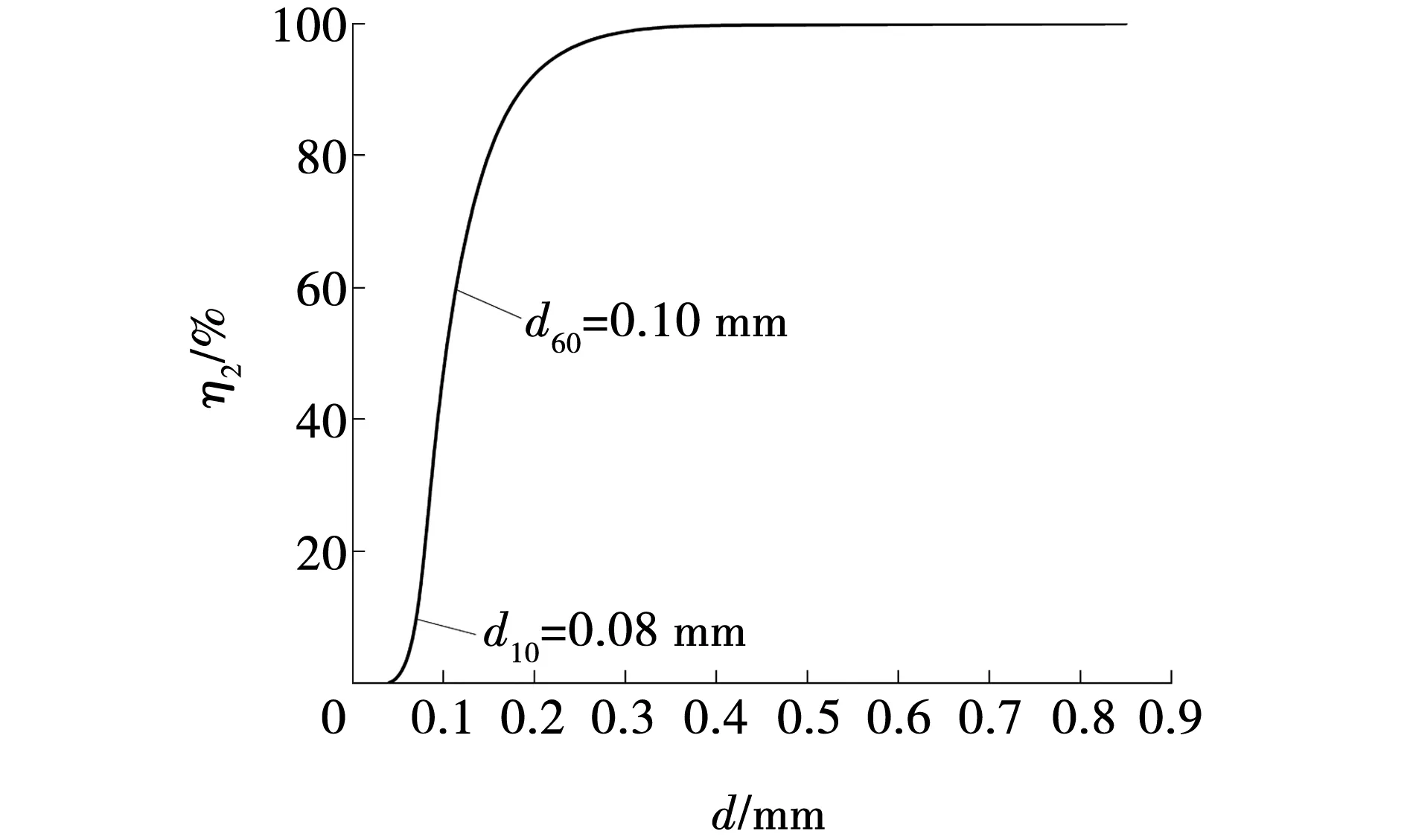
图4 粉煤灰粒径分布曲线Fig. 4 Particle size distribution curve of fly ash

1.3 水泥与外加剂

使用的水泥为鹿鼎集团哈尔滨水泥有限公司生产的虎鼎牌32.5号复合硅酸盐水泥。为高浓度胶结充填材料专门研制的外加剂，由速凝剂、缓凝剂、早强剂、减水剂以质量比为6∶1∶3∶10混合而成，添加量一般占水泥质量的0.005～0.020。

2 混合料级配分析

由以上分析可知，再生骨料和粉煤灰级配均不良，必须混合起来以改良级配，减小孔隙率，增大堆积密实度，同等强度下，以减少水泥用量。实验前必须对两种集料以一定质量比混合后进行筛分实验，然后得出Talbol级配指数进行分析评价。

将粉煤灰与再生骨料以质量比k为0.5、0.4、0.3、0.2、0.1、0.05、0.02均匀混合后进行筛分实验，粒径负累计分布拟合曲线的Talbol级配指数分别为0.30、0.34、0.38、0.44、0.51、0.57、0.61，且R2均大于0.90，如图5所示。由图5可知，随着混合料中粉煤灰占比的升高，Talbol级配指数n随之降低；反之，混合料中再生骨料的占比越高，n随之升高。根据n为0.30～0.60时，级配更加合理的结论可知，粉煤灰与建筑垃圾混合料质量比在0.05～0.50之间，两种集料的密实度较佳。

图5 粉煤灰与再生骨料不同质量比的混合料粒径分布及拟合曲线Fig. 5 Particle size distribution and fitting curves of mixture with different mass ratios of fly ash and recycled aggregate

3 充填材料配合比正交实验

3.1 实验方案

根据前期大量基础性实验结果，设计水泥作为胶结剂，占材料总质量的8%，实验因素取外加剂与水泥的质量百分比(外泥比A)、粉煤灰与再生骨料的质量比(灰骨比B)、充填材料水固质量比C、再生骨料含泥量D(<0.075 mm再生骨料粒径与其总质量的比值)，4个因素也称为自变量，选用L16(45)正交表，各因素分别取4个水平，如表1所示。

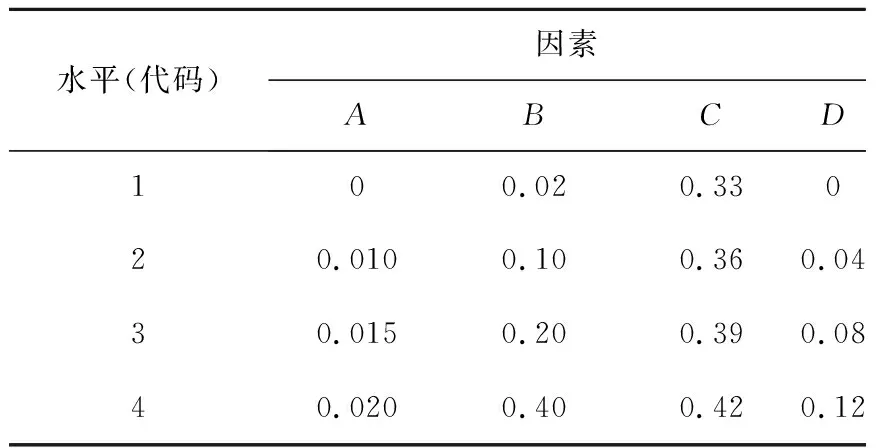
表1 正交实验Table 1 Orthogonal experiment

3.2 结果与分析

3.2.1 实验结果

根据正交实验方案，称取水、固体原材料，充分搅拌得到胶结充填浆料。浆料一部分倒入坍落桶测其塔落度S，一部分浆料倒入贯入阻力仪试模测其初凝时间t。剩余浆料倒入100 mm×100 mm×100 mm的方形塑料试模，标准养护后测其28 d的单轴抗压强度σ28。实验方案及结果如表2所示。

表2 正交实验方案及结果Table 2 Orthogonal experiment scheme and results

3.2.2 极差分析

采用极差分析法对所测得的充填浆料基本性能进行分析，可以确定因素的不同水平对考察指标的影响，极差越大说明该因素水平对试验考察指标产生的影响作用越显著，或者说该考察指标对该影响因素敏感性较强。

(1)坍落度

计算各因素水平对应坍落度平均值和极差，各因素水平与充填浆料坍落度之间的关系如图6所示。

由图6可知，外泥比A随着水平的增大，坍落度值随之急速增加，其极差为RA=97.75 mm，说明专用外加剂可显著增加充填浆料的坍落度。灰骨比B随水平的增加，坍落度先增大、后减小，其阈值为灰骨比B的3水平，即混合料Talbol级配指数为0.44，其极差RB=25.75 mm。水固比C随水平的增大，坍落度随之增大，但水平1到水平2对应坍落度增加的速率小于水平2到水平4，其极差RC=47.75 mm。含泥量D随着水平的增加，坍落度逐渐减小，其极差RD=27 mm，说明粒径小于0.075 mm的微细粉含量的增加会增大充填浆料的黏聚力，从而降低浆料的坍落度。

图6 各因素水平与坍落度的关系 Fig. 6 Relationship between level and slump of each factor

根据极差值大小，可知因素A对初始料浆的坍落度大小的影响作用最明显，即坍落度对因素A最敏感。各因素对浆料坍落度影响作用的主次顺序为A>C>D>B。

(2)初凝时间

计算各因素水平对应充填浆料初凝时间的平均值和极差，各因素水平与充填浆料初凝时间之间的关系如图7所示。由图7可知，外泥比A随着水平的增大，初凝时间先减小后急速增加，其极差RA=100.06 min，说明在充填浆料中加入占水泥质量1%以内的专用外加剂可显著缩短浆料的初凝时间。灰骨比B随水平的增加，初凝时间显著缩短，极差RB=83.7 min，其原因可能是大量粉煤灰吸收大量水分，水泥的水化时间减少导致。水固比C随水平的增大，初凝时间随之增大，但水平1到水平2对应初凝时间增加的速率小于水平2到水平4，其极差RC=38.45 min。含泥量D随着水平的增加，坍落度逐渐减小，其极差值RD=22 min,说明粒径<0.075 mm的微细粉含量增加会缩短充填浆料的初凝时间。

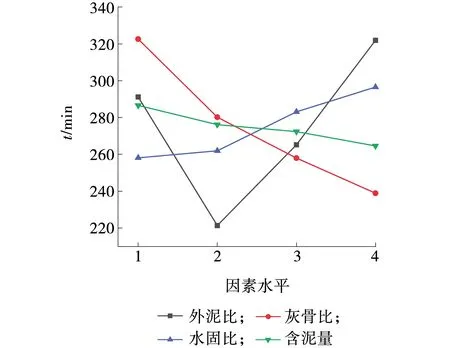
图7 各因素水平与初凝时间的关系 Fig. 7 Relationship between levels of various factors and initial setting time

根据极差值大小，可知因素A对充填料浆的初凝时间影响作用最明显，即初凝时间对因素A最敏感。总之，各因素对浆料初凝时间影响作用的主次顺序为A>B>C>D。

(3)抗压强度

计算各因素水平对应充填浆料28 d抗压强度的平均值和极差，各因素与充填浆料坍落度之间的关系如图8所示。

图8 各因素水平与σ28的关系 Fig. 8 Relationship between levels of various factors and σ28

由图8可知，外泥比A随着水平的增大，28 d抗压强度先增加后减少，再增加，其阈值分别为水平2和水平3，即外泥比为0.01和0.015，其极差RA=0.57 MPa，说明外加剂可增加充填材料的抗压强度，但是掺量需在合理范围内。灰骨比B随水平的增加，28 d抗压强度先急速增大、后减小，极差RB=0.89 MPa，其阈值为水平3，即灰骨比为0.2，说明粉煤灰与再生骨料混合料合理级配会显著增加充填材料的抗压强度。水固比C随水平的增大，28 d抗压强度先增大、后急剧减小，其极差RC=0.83 MPa,其阈值为水平2，即水固比为0.27，说明该水固比为水泥充足水化所需水量。含泥量D随着水平的增加，28 d抗压强度先急速减少，后维持不变，然后再减少，呈“台阶”状，其极差RD=0.50 MPa,说明粒径<0.075 mm的微细粉含量增加会减小充填材料的28 d抗压强度，尤其是在含泥量为0～4%、8%～12%时，其削弱抗压强度作用更加明显。

根据极差值大小，可知因素B对充填料浆的28 d抗压强度影响作用最明显，即28 d抗压强度对因素B最敏感。总之，各因素对28 d抗压强度影响作用的主次顺序为B>C>A>D。

3.2.3 拟合分析

应用DPS7.05数理统计软件对16组正交实验方案所获得的实验结果进行二次多项式逐步回归，得到了坍落度S、初凝时间t、28 d抗压强度σ28与各因素水平(代码)的回归模型，即

S=5.73+52.42A+69.19C-12.40D-

13.76AC+4.15AD-1.80BC-5.05CD，

(1)

t=498.66-177.88A+12.05B-51.57C+

2.03D+44.40A2+0.40B2+10.22C2+

0.63D2-3.62AB-6.61AC-1.46AD-

15.44BD+10.70CD，

(2)

σ28=0.70+0.45A+0.24B+1.73C-0.09A2-

0.17B2-0.24C2+0.10AB-0.07AC-

0.04AD+0.18BD-0.21CD。

(3)

图9 回归模型计算值与实验值的对比 Fig. 9 Comparison between calculated values of regression model and experimental values

由图9可知，除个别模型计算值外，坍落度模型、28 d抗压强度模型计算值与实验值的相对误差基本在-8%～+8%范围内，初凝时间模型相对误差在-3%～+3%范围内，说明回归模型的计算值接近实际值，从而证明了模型的准确性。

4 工业配比与力学特性

4.1 工业配比的确定

以黑龙江七台河矿区为例，井工开采平均深度为400 m左右，充填管路长度一般在2 000 m以内。以浆料平均流速为0.6 m/s计算，浆料在管路中流动时间在60 min以内。根据七台河龙湖矿胶结充填开采实践经验，如果要保证高浓度胶结充填材料的泵送性，其浆料的坍落度一般为210～220 mm。如果要保证充填材料充填后8 h内快速完成拆模、上覆岩层无明显破断、沉陷，充填材料初凝时间为300 min内，28 d抗压强度需大于3 MPa。

根据上述回归模型以及现场要求，考虑经济、早期强度最优的原则。自变量约束条件为外泥比A、灰骨比B、水固比C水平为1～4，再生骨料含泥量D水平分别为1～2、2、2～3、3、3～4。因变量坍落度S、初凝时间t、28 d抗压强度σ28的约束条件分别为210 mm≤S≤220 mm、60 min≤t≤300 min、σ28取最大值且≥3 MPa。

将回归模型、约束条件等代入Matlab和声搜索(Harmony search, HS)智能优化算法，进化迭代设为100次，可得到外泥比、灰骨比、水固比水平的3个随机最优配比，及其对应的坍落度、初凝时间、28 d抗压强度，如表3所示。

由表3可知，当再生骨料含泥量D水平约束条件为1～2时，优化方案中含泥量D的水平均为1，说明在该约束条件下，强度取最大值，含泥量为0。当含泥量D水平的约束条件为2时，较约束条件为1～2时外泥比A和灰骨比B水平均有明显增加，且坍落度基本无变化，初凝时间增加18%，28 d抗压强度减少10%。当再生骨料含泥量D水平为2～3时，初凝时间较D水平为2时延长3%，其它自变量与因变量均没有明显变化。当再生骨料含泥量D水平为3时，较D水平为2～3时水固比C有一定降低，且初凝时间降低8%左右。当再生骨料含泥量D水平为3～4时，较D水平为3时，水固比有一定降低，初凝时间降低22%左右。

表3 最优配比Table 3 Optimal ratio

总之，随着再生骨料含泥量的增加，最优配比的水固比呈逐渐减小的趋势，初凝时间呈先增大后减小的规律。且所有最优配比28 d抗压强度均大于3 MPa，在再生骨料含泥量为0时最大，当含泥量增大时，强度减小不明显。

工业配比需在最优配比的基础上考虑材料成本。建筑垃圾破碎后的天然含泥量为8%，粉煤灰无加工成本。因此，建筑垃圾胶结充填材料含泥量取8%，水固比取较大值，灰骨比取较大值，外泥比取较小值。综合以上因素，建筑垃圾-粉煤灰胶结充填材料的工业配比选择外泥比、灰骨比、水固比、再生骨料含泥量水平(代码)分别为3.86、3.39、1.75、3.00，具体值为0.019、0.278、0.353、0.080，则各原材料占比为：水泥8%、外加剂0.15%、水26.06%、再生骨料51.48%、粉煤灰14.31%。

充填材料的工业配比通过坍落度实验、贯入阻力仪实验、抗压实验分别测得充填材料的坍落度为213 mm、初凝时间为260 min、28 d抗压强度为3.40 MPa，满足现场对充填材料的性能要求。

4.2 力学特性

通过压力试验机可测得依据工业配比制作试样各龄期应力-应变曲线，如图10所示。由图10可知，充填材料3、7、24、28 d龄期的抗压强度分别为0.94、1.89、2.82、3.40 MPa。各龄期的应力-应变曲线呈现共同特征，其可划分为4个阶段：①压缩段，应力与应变呈正变关系，曲线呈上凹型，应力变量逐渐大于应变变量；②弹性段，应力与应变基本呈线性正变关系，斜率基本保持不变；③塑性变形段，应力与应变呈正变关系，曲率与应力呈反变关系，直至达到峰值强度；④屈服破坏段，应力与应变呈反变关系，试样出现明显破裂，直至完全破坏丧失强度。各龄期试件完全破坏后仍具有较高的残余强度，由此可见，充填材料具有较好的承载特性。

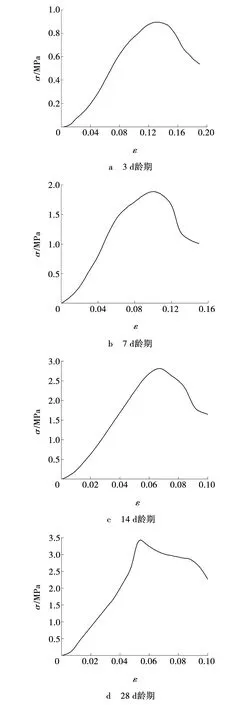
图10 不同龄期应力-应变曲线Fig. 10 Stress-strain curve at different ages

各龄期充填材料屈服后的破坏特征如图11所示。由图11可知，随着养护龄期的增加，水泥水化不断进行，试块强度不断增高，试块中的裂纹数量逐渐增多，裂纹的宽度也逐渐增大。养护龄期为3 d时，裂纹主要集中在试件上部，随着养护龄期的增加，裂纹逐渐向下发展，养护龄期为14、28 d时，开始出现贯通裂缝。各养护龄期试块屈服后均有平行于加载方向以及与加载方向夹角约为45°的裂缝，说明试件破坏形式表现为劈裂破坏与剪切破坏共存。

图11 各龄期试块的破坏特征 Fig. 11 Failure characteristics of test blocks at various ages

5 结 论

(1)混合料达到最佳密实度时，废弃粉煤灰、再生骨料的质量比为0.05～0.5。各因素对浆料坍落度、初凝时间、28 d抗压强度影响作用的主次顺序分别为A>C>D>B,A>B>C>D，B>C>A>D。外泥比A和灰骨比B即外加剂掺量和混合料级配是影响砖混类建筑垃圾-粉煤灰胶结充填材料特性的决定因素。

(3)随着再生骨料含泥量的增加，最优配比的水固比呈逐渐减小的趋势，且初凝时间呈先增大后减小的规律。所有最优配比28 d抗压强度均大于3 MPa，在再生骨料含泥量为0时最大，当含泥量增大时，强度减小不明显。

(4)考虑成本因素得到的砖混类建筑垃圾-粉煤灰胶结充填材料工业配比，外泥比0.019，灰骨比0.288，水固比0.323，再生骨料含泥量0.080，水泥占材料质量的8%,建筑垃圾及废弃粉煤灰占材料质量的65.79%，固体质量占比为75.59%，成本较低，可消化大量废固。

(5)最优工业配比下砖混类建筑垃圾-粉煤灰胶结充填材料的3 d抗压强度为0.94 MPa，14 d内抗压强度增长迅速，28 d抗压强度为3.40 MPa。各龄期试块屈服时破坏形式表现为劈裂破坏与剪切破坏共存，屈服后仍有较高的残余强度，说明充填材料具有较好的承载特性。