循环加卸载下砂岩的力学特性和声发射特征

秦 涛， 任 凯

(黑龙江科技大学 黑龙江省普通高等学校采矿工程重点实验室， 哈尔滨 150022)

0 引 言

岩土工程中，岩石往往处于反复加卸载荷的复杂应力环境中，例如，地下硐室的开挖、回采巷道的掘进、边坡开挖等，岩石均经历着交替加卸载荷的过程。目前，针对复杂应力下岩石的力学特性研究很多，葛修润等[1]对三种不同类岩石开展周期循环实验，对比分析其疲劳破坏机理。李杰林等[2]对风化花岗岩进行单轴循环实验，研究了循环次数与岩石力学参数的关系。周垒[3]对大理岩进行两种不同加载方式的循环实验，从介观角度来分析大理岩的变形破坏机理。Guo等[4]研究了岩石在单轴循环作用下的力学性质和变形机理，得出随着循环次数的增加，应力-应变曲线形成的滞回环向应变增加的方向移动。秦涛等[5]对砂岩进行三轴循环实验，表明指数函数可以反映耗散能损伤变量情况。刘忠玉等[6]研究循环加卸载下层理煤岩的变形破坏，分析了变形破坏过程中的残余变形和弹性模量。谷中元等[7]开展了室内花岗岩单向循环加卸载实验，并用红外监测设备，揭示了岩石破坏的机制。

岩体在受到外部载荷作用下，产生损伤、断裂、失稳破坏的同时以弹性波的形式将岩体储存的部分应变能释放，这一种自然现象被称为“声发射”[8]。采用声发射手段研究岩石的变形破坏受到许多学者的青睐。来兴平等[9]对天然互层砂岩开展了单轴分级循环加卸载实验,分析了自然和饱水状态下互层砂岩的声发射特性。刘刚等[10]以宝泰隆宏泰煤样为研究对象，分析了循环加卸载下煤样的力学特性，并通过声发射得出煤样的损伤演化规律。包春燕等[11]分析了石灰岩单轴循环加卸载作用下声发射和波速的变化。付斌等[12]对大理岩进行声发射实验，通过Felicity比值变化和b值的变化，分析大理岩的破坏特征。刘建坡等[13]采用声发射研究了循环作用下岩石的损伤，并建立损伤与声发射的数量模型。

综上所述，学者们对不同应力条件下，煤岩体的强度特性、变形特征开展了研究，并借助声发射手段分析其损伤演化规律，取得了一定的研究成果。然而，岩石循环加卸载过程中损伤破裂是一个复杂的过程，岩石损伤破裂受到其弹性参数变化、外部载荷等因素影响，岩石受载过程其自身力学参数随着应力条件发生变化。因此，笔者对砂岩开展卸载阶段应力值恒定，加载阶段应力值逐级增加的循环实验，并使用SH-Ⅱ声发射系统采集砂岩变形破坏过程中的声学信息，得到砂岩的应力-应变曲线、弹性模量和声发射参数，分析砂岩力学特性和声发射特征，为岩石损伤破裂机理研究提供理论依据。

1 实验设备与方案

1.1 试件的制备

把砂岩加工成尺寸为50 mm×100 mm的标准圆柱体试件，如图1所示。为保证实验结论的可靠性，对制备好的试件用Sonic Viewer-SX超声波测试系统和电子天平分别进行波速和质量评估，选取P波波速v和质量相接近的砂岩进行实验，测试结果见表1。

1.2 实验方案

实验使用TAW-2000试验机完成加载，采用SH-Ⅱ声发射系统进行监测，传感器型号为Nano30，实验系统见图2。开展卸载阶段应力值恒定、加载阶段应力值逐级增加的循环实验，其中加载速率和卸载速率均为250 N/s。对5个试件分别开展循环加卸载实验，压力机加载路径如图3所示。

2 循环加卸载力学特性

对循环载荷作用下的砂岩应力-应变曲线和弹性模量进行分析。由于试件SH-21、SH-28、SH-41、SH-42、SH-49的应力-应变曲线特征相似，限于篇幅，文中仅对SH-49试件进行分析。

2.1 应力-应变曲线

砂岩循环实验应力-应变曲线如图4所示。当循环加载应力值达到73.66 MPa时，试件发生破坏，故未获得卸载阶段曲线。不同循环阶段，砂岩加卸载应力应变曲线均呈非线性特征。加载阶段砂岩的应力-应变曲线呈非线性是因为在加载阶段初期，砂岩内部的原始裂纹裂隙闭合，导致曲线呈非线性增加；加载中期，岩石基质部分弹性变形，此时的曲线近似直线，呈线性增加；加载后期，砂岩的应力-应变曲线又呈非线性变化，这是因为岩石发生了塑性破坏，进入了塑性变形阶段。卸载阶段应力应变曲线具有非线性特征是由于在卸载阶段初期，岩石基质部分弹性变形恢复造成应力应变曲线近似呈线性下降，卸载后期随着应力逐渐卸除，微裂纹裂隙的回弹变形，以致卸载曲线表现出明显的非线性特征。

由图4b局部放大的应力-应变曲线可以看出，曲线均表现为上凹型，且随加载上限应力逐渐增加，上凹度也增大。在经历一次循环加卸载后，加、卸载曲线没有完全重合，而是卸载曲线与下一次的加载曲线形成一个闭合环形曲线，这个闭合环形曲线叫“滞回环”。随着循环上限应力的增加，滞回环由疏向密变化，并朝着应变增加的方向后移。这是因为砂岩内部出现不可恢复的塑性损伤变形，且由于上限应力的不断增加，砂岩所受应力越来越大，其原始裂纹进一步扩展发育，新生裂隙也逐渐增多，表现为塑性变形越来越大，损伤逐渐积累，造成滞回环不断向后迁移。

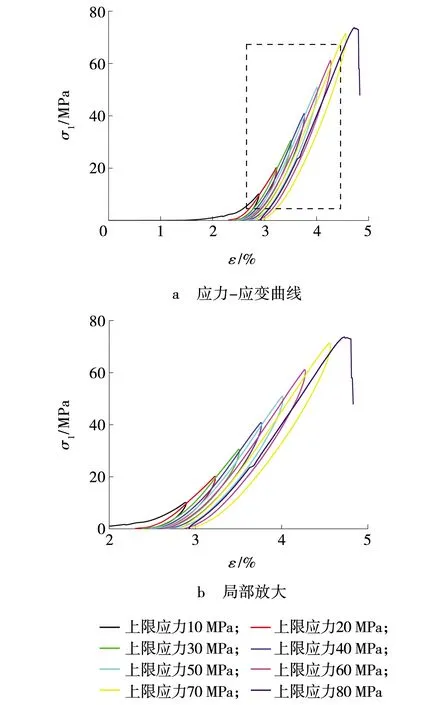
图4 不同加载上限应力-应变曲线Fig. 4 Stress-strain curves of different loading upper limits

2.2 弹性模量

进行弹性模量计算时要考虑循环载荷对岩样造成的损伤，即每次循环加、卸载均发生不可恢复的塑性变形，且随着循环上限应力的增加，岩样的塑性变形加剧，所以分别对加载阶段和卸载阶段弹性区间内进行计算，计算结果如表2所示(E+、E-分别为加卸载阶段弹性模量)。

表2 弹性模量计算结果Table 2 Calculation results of elastic modulus

为进一步研究弹性模量的变化情况，绘制了弹性模量与轴向应力的曲线，并进行拟合，如图5所示。

图5 加卸载弹性模量拟合曲线 Fig. 5 Loading and unloading elastic modulus fitting curve

由图5可以看出，应力水平可以较好地反映E+和E-的变化趋势。随着加载上限应力水平的提高，加载弹性模量和卸载均呈增大趋势。当加载上限应力水平逐渐达到极限值时，弹性模量增大速率逐渐减小，最终趋于一个稳定值。循环过程中，在相同应力水平下，加载弹性模量小于卸载弹性模量，循环加载阶段初期，岩石内部原生裂纹裂隙被严密后，卸载阶段不能完全恢复，卸载弹性模量增大，随着应力水平的提高，二者差值变小。

3 循环应力下声发射特性

3.1 岩石声发射特征

岩石变形破坏过程中，将内部存储的部分应变能以弹性波的方式释放，声发射系统可以接收到释放的弹性波，而传感器能够把机械信号转换为电信号，最终通过波形变化表征岩石内部声发射活动，进而反映岩石内部节理发育扩展和损伤情况。

1950年，德国学者Kaiser J[14]对金属材料压缩时，在后一次加载应力值小于前一次值时，声发射信号几乎没有产生；当超过前一次最大应力值时产生大量的声发射信号，即为Kaiser效应。目前，常用声发射振铃累计数来分析Kaiser效应。因此，通过应力-时间-声发射特征参数曲线(图6)来综合分析Kaiser效应，建立岩石损伤破坏与声发射规律的内在联系，对进一步认识复杂应力路径下岩石变形破坏机理具有重要意义。

由图6a可以看出，声发射主要发生在循环加载阶段，而在卸载阶段中几乎没有发生这种现象，即认为声发射活动在卸载阶段进入“休眠期”。由图6b可以看出，在第1次和第2次加卸载循环时，振铃累计数曲线的增幅较为明显，在第3～6次循环时，振铃累计数曲线的增幅较为平缓，在第7次循环加载上限应力值达到70 MPa之前时，振铃累计数曲线拐点突增，第8次当加载应力达到73.66 MPa时，声发射振铃计数和声发射振铃累计数均达到顶峰。表明循环加载应力值超过上一次加载上限应力值后，岩石产生了不可恢复的损伤变形。岩石每经历一次循环加卸载后会在内部达到新的平衡，此时声发射活动相对平静，累计数曲线变化平缓；随着加载上限应力值增大，原先平衡被打破，使得裂纹裂隙继续扩展发育，寻找下一个平衡，该阶段声发射活动明显。这一现象不断循环直至进入最后的破坏阶段，这些裂纹裂隙最终汇聚贯通形成宏观破断面，振铃累计数达到最值。

图6 声发射活动规律Fig. 6 Activity law of acoustic emission

Kaiser效应分析，在分级循环加卸载条件下，振铃累计数曲线阶梯型变化明显，拐点突出，但是在第4次循环加载阶段(本次循环上限应力大于峰值应力的50%)，加载应力达到28.18 MPa时，振铃累计数出现拐点，其对应的应力小于第3次循环的峰值应力，Kaiser 效应失效，岩石损伤加剧。

3.2 声发射Felicity比

声发射Felicity效应是指在循环加卸载过程中，岩石当前应力值未超过上次加载阶段的上限应力值，但此时声发射振铃计数增加明显，又称为反Kaiser效应。因此，Kaiser效应的有效性可以通过Felicity比值来进行验证，考虑到实验的误差，可认为Felicity比值≥0.9时，Kaiser效应有效[15]。Felicity 比定义为

Ri=σAE/σi-1,

(1)

式中：Ri——循环第i次的Felicity比；

σAE——第i次产生大量声发射对应的应力；

σi-1——第i-1次加载过程中所受的最大应力。

Felicity 比值变化曲线如图7所示。

图7 Felicity 比值变化曲线Fig. 7 Felicity ratio change curve

由图7可知，Felicity比曲线平滑下降，在第3次循环加卸载阶段(上限应力小于峰值应力的50%)，Felicity比由1.525降到0.945，Kaiser效应明显；第4次循环阶段(上限应力大于峰值应力的50%)，Felicity比降为0.863，表明Kaiser效应失效，Felicity效应成立，试件裂纹稳定发展，经历第5、第6、第7次循环加卸载后，Felicity比降为0.758，岩石破坏加剧。

4 结 论

(1)不同上限应力水平下砂岩的加、卸载曲线均表现出明显的非线性变形特征；加卸载曲线形成滞回环，在实验过程中由疏向密变化，并朝着应变增加的方向移动；加卸载曲线均呈上凹型，且上凹度与加载上限应力呈正相关。

(2)随着应力水平的提高，加卸载弹性模量均呈增大趋势，但增大的速率逐渐减小且二者差值也逐渐变小；卸载弹性模量始终大于加载弹性模量，加卸载弹性模量在一定程度上体现了砂岩整体弹性参数的变化。

(3)加载阶段声发射活动明显，而在卸载阶段声发射活动进入“休眠期”；加载前期，当加载上限应力值未超过峰值应力的50%时，Felicity比大于0.9，Kaiser效应明显；当上限应力大于峰值应力的50%时，Felicity比小于0.9，Kaiser效应失效，岩石破坏加剧，说明随循环加卸载应力的增加，岩石内部损伤加剧。