Bn×Um的全纯自同构群

王丽欣

(吉林师范大学 数学学院，吉林 四平 136000)

0 引言

域的全纯自同构群是多复变研究中的重要工具，在研究域的双全纯等价以及Bergman核函数问题上都起到了非常关键的作用，因为全纯自同构群的重要性，也吸引了国内外很多学者的关注和研究.Abraham A Unga在文献[1]中给出了复圆盘上的全纯自同构群.HengJu Ahn等[2]给出了经典对称域上的Hartogs型域的全纯自同构群.Jie Zhao等在文献[3]中给出了Bergman-Hartogs域的全纯自同构群.Hao在文献[4]中给出了拟Hartogs域的全纯自同构.Shuxia Feng等[5]给出了(m，1)-圆域上的全纯自同构群.Hyeseon Kim等在文献[6]中给出了Fock-Bargmann-Hartogs域的全纯自同构群.在此基础上Guo Ting等[7]解决了广义Fock-Bargmann-Hartogs域上全纯自同构的刚性问题.肖金秀等在文献[8]中给出了域B2×B2上的全纯自同构群，并计算了其上的Bergman核函数.金帅[9]用不同的方法给出了域B2×B2上的全纯自同构群.陈永发等[10]利用全纯自同构将边界映为边界这一性质给出了Bn×Um上的全纯自同构群.受文献[9]和[12]的启发，本文将采用不同于[10]中的方法，利用Hartogs型域的全纯自同构以及酉矩阵的性质得到计算Bn×Um全纯自同构的必要条件，进而得到了Bn×Um的全纯自同构群，简化了文献[10]中的计算过程.最后给出Bn×Um全纯自同构的Jacobian行列式.

1 基础知识

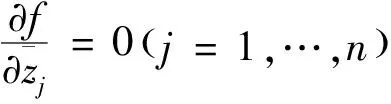
定义2[8]设Ω是Cn中的域，f1,…,fm是Ω上的全纯函数，那么称F=(f1,…,fm):Ω→Cn为全纯映射.如果F有全纯的逆映射F-1，那么F就是双全纯映射.

定义3[9]设Ω是Cn中的域，若F是把Ω映为自身的双全纯映射，则称F是Ω的全纯自同构，简称自同构.Ω的全纯自同构全体记为Aut(Ω)，在映射的复合运算下构成一个群，称为Ω的自同构群.

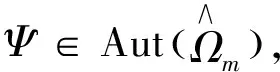
由于Bn×Um可以看成特殊的Hartogs型域，则可得到如下结论：

推论1若f∈Aut(Bn×Um)，则f将Bn×{0}映为自身.

引理2[9](H Cartan定理)设Ω是Cn中包含原点的有界圆形域，如果有F∈Aut(Ω)，且F(0)=0，那么F一定是线性映射.

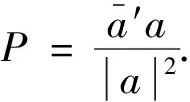
引理4[9]设Ω1和Ω2分别是Cn和Cm中的有界域，Ω=Ω1×Ω2，若用K1，K2，K分别表示Ω1，Ω2和Ω的核函数，那么K=K1K2.

引理5[9]设Ω和Ω1为Cn中的有界域，双全纯映射f把Ω一一地映为Ω1，Ω和Ω1核函数分别记为K(z,ζ)和K(f(z),f(ζ))，那么

K(z,ζ)=

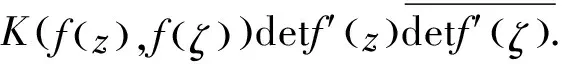
作为上述的特殊情况，当f为Ω的全纯自同构时，

K(z,ζ)=K(f(z),f(ζ))|detf′(z)|2.

引理6[9]设Ω是Cn中的有界域.如果ψ∈Aut(Ω)，那么对任意z∈Ω，有

2 主要结论及证明

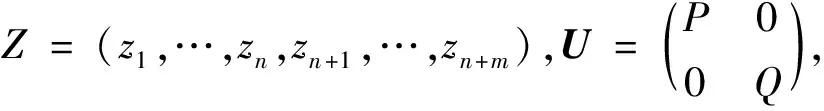
证明由于Bn×Um是包含原点的有界圆型域，f∈Aut(Bn×Um)且f(0)=0，由H Cartan定理可知，f为线性映射，故可设

f=(f1,…,fn,fn+1,…,fn+m)=

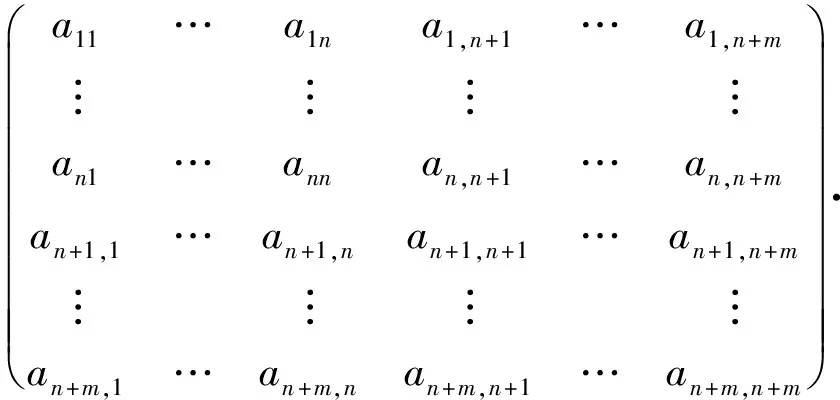
取点列

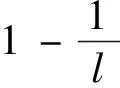
当j=1时，

则当l→∞时，

的极限点在∂Bn×{0}上，那么f(z(1))的极限点也在∂Bn×{0}上，即

f(z(1))=

(a11,…,an1,an+1,1,…,an+m,1)→∂Bn×{0}，

因此an+1,1=…=an+m,1=0.同理可得an+1,2=…=an+m,2=0，…，an+1,n=…=an+m,n=0.取Z=(z1,…,zn,0,…,0)∈Bn×{0}，则有

f(Z)=(f1,…,fn,fn+1,…,fn+m)=

(a11z1+…+a1nzn,…,an1z1+…+

annzn,0,…,0)∈Bn×{0}.

记

(a11z1+…+a1nzn,…,an1z1+…+annzn)T=

Pz∈Bn，

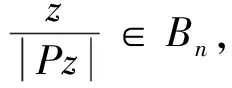
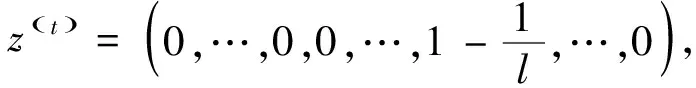
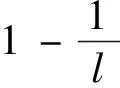
当t=n+1时，

则当l→∞时，

的极限点在{0}×∂Um上，那么f(z(n+1))的极限点也在{0}×∂Um上，即

f(z(n+1))=

(a1,n+1,…,an,n+1,an+1,n+1,…,an+m,n+1)→

{0}×∂Um，

则a1,n+1=…=an,n+1=0.

同理a1,n+2=…=an,n+2=0,…,a1,n+m=…=an,n+m=0.

取Z=(0,…,0,zn+1,…,zn+m)，其中(zn+1,…,zn+m)∈Um，则Z∈{0}×Um.则有

f(Z)=

(0,…,0,an+1,1zn+1+…+an+1,n+1zn+m,…,

an+m,n+1zn+1+…+an+m,n+mzn+m)∈{0}×Um，

则

|an+1,n+1zn+1+…+an+1,n+mzn+m|≤1，…，

|an+m,n+1zn+1+…+an+m,n+mzn+m|≤1.

设akj=|akj|eiφj，并选取z=reiφj(0

|an+1,n+1+…+an+1,n+m|≤1,

|an+2,n+1+…+an+2,n+m|≤1,…,

|an+m,n+1+…+an+m,n+m|≤1.

由于max|akj|=1(k,j=n+1,…,n+m)，

取j=n+1，则有相应的k(n+1)，使得

|ak(n+1),n+1|=1，

则ak(n+1),j=0,j=n+2,…,n+m.再取j=n+2，则有相应的k(n+2)，使得

|ak(n+2),n+2|=1，

可知

ak(n+2),j=0,j=n+1,n+3,…,n+m，

这里

k(n+1)≠k(n+2)，

否则会出现

|ak(n+1),n+2|=1，

这与前面得到的ak(n+1),n+2=0矛盾.按照上面方式继续下去，对于每个j=n+1,…,n+m都存在k(j)，使得

|ak(j),j|=1，ak(j),k=0，

其中j≠k.这里(k(n+1),…,k(n+m))是(n+1,…,n+m)的一个置换.由以上讨论可知|Q|=1，那么Q是酉矩阵并且每行每列有且仅有一个模长为1的非零元素.至此定理1得证.

定理2[6]设f∈Aut(Bn×Um)，f(a)=f(a′,an+1,…,an+m)=0，a′=(a1,…,an)，则

f(z)=

其中P,θ1,…,θm是和f有关的n维酉矩阵和幅角，(τ(n+1),…,τ(n+m))是(n+1,…,n+m)的置换.

证明由引理2可知φa′(z′)∈Aut(Bn)，记

h(z)=

作函数

显然g∈Aut(Bn×Um)，从而有F=g°f-1∈Aut(Bn×Um)，且F(0)=g(a)=0.由定理1可知必有矩阵U使得F(z)=Uz，且

从而f(z)=F-1(g(z))=g(z)U-1，得证.

定理3Bn×Um的Bergman核函数是

K(z,ζ)=

并且自同构f(z)的实Jacobian为

|detf′(z)|2=

证明Bn的核函数为

令n=1，则可得到单位圆盘的核函数：

因为在这里多圆柱是由m个单位圆盘构成的乘积域，由引理4即可得到多圆柱Um的核函数为

即可得Bn×Um的Bergman核函数为

K(z,ζ)=

根据引理6可算得自同构F(z)的实Jacobian为

|detf′(z)|2=