一类广义Petersen图的2-距离染色
陈海钰
(兰州职业技术学院,甘肃 兰州 730070)
0 引言
图的染色问题是图论研究的重要问题之一.距离染色的概念最早由F Kramer和H kramer在文献[1-2]中提出,它是顶点染色理论的一种推广.图G(V,E)的2-距离染色是指正常的顶点染色,且满足距离不大于2的任意两个顶点染不同的颜色,记作(r,2)-DC,其中r是所用颜色数,满足(r,2)-DC的最少颜色数称为2-距离色数,记作χ2(G).文献[4-7]研究了一些特殊图类的k-距离染色;文献[8]概述了有关平面图的2-距离染色的研究结果.文献[9]确定了稀疏平面图的2-距离染色上界.本文研究了一类广义Petersen图P(n,2)的2-距离染色,并确定了P(n,2)的2-距离色数.
1 定义及引理
定义1[10]设图G的顶点集为{x0,x1,…,xn-1;y0,y1,…,yn-1},边集为{xixi+1,xiyi,yiyi+t|i=0,1,…,n-1},其中下标取模n,且n≥5,0 引理1[4] 对于广义Petersen图P(n,2),令Y0={yi|i为偶数},Y1={yi|i为奇数},X={x0,x1,…,xn-1},则 由广义Petersen图的定义容易得到如下性质. 未做说明的符号参见文献[11]. 定理1χ2(P(5,2))=10. 证明因为P(5,2)就是Petersen图,而Petersen图是直径为2的10个顶点的图. 定理2χ2(P(n,2))=5,当且仅当n=10m(其中m≥1为整数). 证明 (1)充分性 由于P(n,2)有C5子图,所以 χ2(P(10m,2))≥5. 要证明χ2(P(10m,2))≤5,只需要给出P(10m,2)的一个(5,2)-DC.P(10,2)的(5,2)-DC如图1所示.如果m>1,按照此方案循环染色即可. 图1 P(10,2)的(5,2)-DC (2)必要性 由于x0,x1,x2,y2,y0导出的子图为5-圈,不妨用颜色1,2,3,4,5染,则y1可用的颜色有{4,5},x3可用的颜色有{1,5}.若c(y1)=4且c(x3)=1(c(xi)表示xi所染的颜色),则y4没有可用的颜色,故只能c(y1)=4且c(x3)=5,或者c(y1)=5且c(x3)=1.不放设c(y1)=4且c(x3)=5,此时,P(n,2)的所有顶点的染色方案确定且唯一.即x0,x1,…,xn-1循环染颜色1,2,3,5,2,4,5,1,4,3;y0,y1,…,yn-1循环染颜色5,4,4,1,1,3,3,2,2,5.所以,当n不是10的倍数时,总存在P(n,2)的顶点没有可行的颜色.同理可证当c(y1)=5且c(x3)=1时的情形. 定理3若n≠5且n≡0(mod 10)时,χ2(P(n,2))=6. 证明分以下3种情形,给出P(n,2)的(6,2)-DC,假设颜色集合为{0,1,2,3,4,5}. 情形1n≡0(mod 3). 令n=3m(m≥2).若m≡0(mod 2),令m=2l(l≥1),那么n=6l≡0(mod 2),Y0,Y1的导出子图为两个不相交3l-圈,又因为X的导出子图为3m-圈,所以X中的顶点从x0开始,依次按照下标从小到大的顺序循环染颜色1,2,3;Y0中的顶点从y0开始,依次按照下标从小到大的顺序循环染颜色4,5,6;Y1中的顶点从y1开始,依次按照下标从小到大的顺序循环染颜色4,5,6(如图2所示). 图2 P(6l,2)的(6,2)-DC 若m≡1(mod 2),令m=2l+1(l≥1),那么 n=3(2l+1)≡1(mod 2), Y的导出子图为一个n-圈.又因为X的导出子图为3m-圈,所以X中的顶点从x0开始,依次按照下标从小到大的顺序循环染颜色1,2,3;Y中的顶点从y0开始,依次按照在Y的导出n-圈中顺序循环染颜色4,5,6(如图3所示). 图3 P(3(2l+1),2)的(6,2)-DC 情形2n≡1(mod 3). 令n=3m+1(m≥2).若m≡0(mod 2),令m=2l(l≥1),那么n=6l+1≡1(mod 2),Y的导出子图为一个n-圈,且 |Y0|=3l+1,|Y1|=3l. 图4 P(6l+1,2)的(6,2)-DC 图5 P(6l+4,2)的(6,2)-DC 情形3n≡2(mod 3). 令n=3m+2(m≥2).若m≡0(mod 2),令m=2l(l≥1),那么 n=6l+2≡0(mod 2), 图6 图4P(6l+4,2)的(6,2)-DC 图7 图4P(6l+2,2)的(6,2)-DC 综上,结论得证. 当n>5时,由于P(n,d)是三正则图,与任一顶点距离为2的顶点最多有9个,依据P(n,d)的特点,在这些顶点中至少存在两个距离大于2的顶点,所以有χ2(P(n,d))≤9.鉴于已经证明的结论,提出下面的猜想: 猜想当n>5时,有χ2(P(n,d))≤6.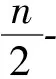
2 主要结论