过江盾构隧道止水密封垫力学性能试验及数值模拟

张天 霍永鹏 吴悦 殷召念 文彦鑫 晏启祥

1.西南交通大学交通隧道工程教育部重点实验室，成都 610031；2.中铁二院工程集团有限责任公司，成都 610031

近年来，我国规划和建设中的水下盾构隧道工程逐渐呈现出埋深大、高水压、大直径和地质条件复杂等特点［1-3］。外水压力的不断增大对传统盾构隧道防水体系带来极大挑战。盾构隧道主体通常是由钢筋混凝土管片和螺栓拼装而成的衬砌结构，在长期的复杂地质和高水压的作用下，接缝渗漏水已成为妨碍隧道正常使用的严重问题［4-5］。在接缝处嵌入橡胶弹性密封垫是目前管片接缝防水的主要手段，依靠密封垫弹性压密，以接触面压应力来止水。

防水密封垫的研究方法主要分为两种：室内试验法和数值模拟法。承受较高水压的大直径水下盾构隧道对密封垫的拼装和防水性能具有更高的要求，在进行盾构隧道接缝防水密封垫的设计时，一般采用数值模拟的方法对密封垫设计方案进行仿真分析和结构优化，然后进行室内试验验证，这样可以提高设计效率和质量。

室内试验方面，赵明等［5］对多组密封垫的装配力及一字缝、T型缝防水性能进行试验研究，从试验结果得出密封垫硬度和沟槽填充率直接影响密封垫防水性能。拓勇飞等［6］提出了一种针对高水压大直径盾构隧道的弹性密封垫设计流程与研究方法，并对具体工程设计了几种具有不同截面形式的密封垫，通过不同橡胶硬度条件下的一字缝防水能力试验、装配力补充试验对管片接缝防水性能进行了研究。董林伟等［7］针对一种常用的管片接缝密封垫开展了耐水压力试验，对密封垫的防水机理进行了分析和相关推导，分析得出密封垫的防水性能由挤压密封阻力和自密封阻力两部分组成。数值模拟方面，张稳军等［8］利用室内试验和数值模拟对密封垫防水性能进行了研究，并建立盾构隧道三维荷载-结构模型探究了在施工荷载下接缝变形特性及其对密封垫防水性能的影响。周文锋等［9］建立“T 字缝”流固耦合计算模型，通过分析密封垫间平均接触应力分布特征及渗流规律确定了接缝处易渗漏位置，并推导出了“T 字缝”密封垫渗漏临界水压计算公式。

以上研究有助于对密封垫防水原理、防水性能的影响因素、密封垫装配力变化过程和接触面上接触应力的分布状况等有更加深刻的认识，但在研究过程中密封垫数值模拟结果往往和室内试验结果存在较大差异，实际工程仍以室内试验结果作为密封垫防水性能的依据，而数值模拟结果则作为定性判断依据［5］。造成这个问题的原因主要有：有限元分析中现有密封垫橡胶材料本构模型不够准确，并且主要通过公式计算获取力学参数；实际密封垫表面与管片表面状态和连接关系较复杂，并且在有水和无水、施工期和运营期情况下差异较大［10-11］。

本文依托上元门越江隧道工程，制定了设计防水压力为1.7、2.5 MPa 的7 种不同截面形式的密封垫设计方案，开展密封垫装配力模拟试验，并基于室内试验结果，利用数值方法模拟密封垫的压缩过程，分析密封垫两端边界条件对计算结果的影响，为橡胶本构模型的选择提供参考，分析结果可作为研究密封垫力学性能的定性参考依据。

1 密封垫设计方案

1.1 工程概况

1.2 密封垫截面设计

密封垫常用截面形式有梯形、梳形和中孔形。本次密封垫设计方案采用主流的中孔形截面，为了满足该工程不同区段的防水要求，分别设计了7 种截面形式的密封垫，见图1。密封垫材料均为炭黑填充橡胶，该橡胶以三元乙丙橡胶为基本胶种，通过加入炭黑、助化剂等材料炼化制得。如图1 所示密封垫1—密封垫4 高为26 mm，由于管片沟槽的高度为15 mm，因此随管片拼装后最大压缩量为22 mm，压缩率均为42.3%，设计用于抵抗1.7 MPa 水压；密封垫5—密封垫7 高度为28 mm，最大压缩量为26 mm，设计用于抵抗2.5 MPa水压。

图1 不同密封垫截面尺寸示意（单位：mm）

从截面形式可以看出，7 种密封垫中，密封垫5—密封垫7三种密封垫高度较高，压缩率为46.4%，比前4 种密封垫的压缩率大4.1%。密封垫1—密封垫6 的开放孔均为底部梳齿间形成的孔洞，密封垫7 底部梳齿由一层橡胶底面连接，梳齿间的开放孔变为封闭孔，增加了密封垫和管片的底部接触面积，在实际工程中密封垫底面和管片沟槽黏结后，有利于提高整体稳定性，预防密封垫底部形成渗水通道。

2 室内装配力试验

对于上述7 种密封垫，使用三元乙丙橡胶制作“一”字形密封垫试件，在室内开展压缩应力模拟试验。测试各密封垫从未压缩状态到压缩至张开量为0 mm时的装配力，每种密封垫测试三次，试验步骤为：

Step1 先把试样放在试验装置的沟槽内，上下合起放入导向套内，并使用限位器限制试样两端位移。

Step2 以50 mm/min 速度压缩试样，直至压缩间隙接近0 mm，再以相同速度放松试样，如此反复压缩和放松试样重复两次。

Step3 第三次为正式试验，应绘出压缩量-荷载曲线。

将三次试验结果的平均值绘制压缩量-装配力曲线，见图2。可知，当接缝张开量为0 mm 时，密封垫1—密封垫4 的最大装配力（即闭合压力）分别为64.0、55.1、49.4、40.1 kN/m；密封垫5—密封垫 7 的最大装配力分别为59.7、64.1、74.2 kN/m。在同一管片沟槽形式下，密封垫高度越高，其最大压缩量越大，闭合压力越大。

初入田野者，容易囿于自我知识之“先见”，对于村落民俗匆遽地下判断。比如对于村民的信仰活动，或评判其是否迷信，或质疑其佛道混杂，而不能理解这些活动与中华文化传统、地方社区公益传统、村民生活实用等之间的内在关联。上述知识“先见”，其实是基于对中国社会的肤浅理解，本来是应该在田野调查过程中被反思的。更何况，即使是在看似荒诞不经的言行背后，也往往蕴含着村民的真实心态，是解读村落心史的难得资料。

图2 密封垫压缩量-装配力曲线

3 数值模拟

3.1 橡胶本构模型

目前在与盾构隧道防水密封垫相关的有限元分析中，Mooney‐Rivlin 和Yeoh两种超弹性体本构模型是最为常用的两种本构模型。Mooney‐Rivlin 模型几乎可以模拟所有橡胶材料的力学行为，而Yeoh模型则比较适合模拟炭黑填充橡胶的大变形行为［12-13］。

3.1.1 Mooney‐Rivlin模型

Mooney‐Rivlin 模型是一种经典的基于连续介质唯象理论的本构模型，对几乎所有橡胶材料的力学行为的模拟均具有较好的适用性。Mooney‐Rivlin 模型的应变能密度函数为［14］

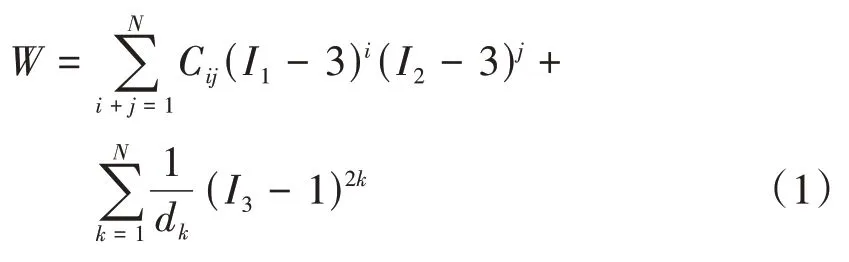
其典型的二阶形式为

式中：Cij、dk、N为材料常数，由材料试验确定，i、j、k为指标符号；I1、I2、I3为 Cauchy‐Green 变形张量不变量；J为变形后与变形前的体积比，对于不可压缩材料，J=1。

Mooney‐Rivlin 模型一般适用于应变约为100%（拉伸）和30%（压缩）的中小变形情况。根据相关规范和参考文献的力学性能参数计算公式［9，12，15］，推荐采用表1中不同硬度橡胶密封垫的Mooney‐Rivlin模型力学计算参数。

表1 不同硬度橡胶的Mooney-Rivlin模型力学计算参数

3.1.2 Yeoh模型

Yeoh 通过试验研究建议应变能密度函数不包含第二应变不变量，并提出一个三次应变能密度函数式。Yeoh 模型在准确预测单轴和平面拉伸试验应力应变关系的同时，却在预测等双轴拉伸的应力-应变关系时表现出“偏软”的现象。因此，Yeoh 模型在处理较大变形的复杂应变状态时，会出现较大的偏差。Yeoh模型的应变能密度函数为典型的三项参数形式

根据不同硬度的三元乙丙橡胶材料试验结果，推荐采用表2 中不同硬度橡胶密封垫的Yeoh 本构模型力学计算参数。

表2 不同硬度橡胶密封垫的Yeoh本构模型力学计算参数

3.2 模型建立

依托上元门越江隧道的防水密封垫设计方案，分别对其中设计防水压力为2.5 MPa的密封垫进行建模计算：圆形开孔为主的密封垫5，三角形开孔为主的密封垫6。使用ABAQUS 有限元软件分别建立一字缝处防水密封垫，密封垫长度和室内装配力模拟试验中试件长度一致，为200 mm。模型中混凝土管片沟槽表面采用离散刚体R3D4 单元进行模拟，密封垫则采用C3D8R 实体单元。弹性橡胶密封垫和混凝土管片沟槽之间以及不同密封垫之间采用面面接触，密封垫自身外表面和内部孔洞表面采用自接触。接触对法向设置为硬接触，切向设置为罚函数。不同密封垫有限元模型网格划分后的截面见图3，一字缝处防水密封垫有限元模型见图4。

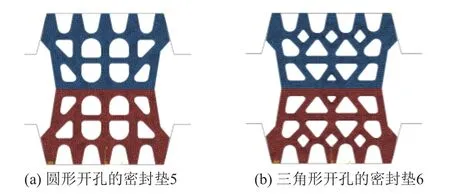
图3 不同密封垫有限元模型截面

图4 一字缝处防水密封垫有限元模型

3.3 橡胶本构与模型边界选择

为分析前述两种本构模型对于本工程中不同密封垫压缩过程模拟的适用性，将室内装配力模拟试验的压缩量-装配力曲线与采用不同橡胶本构的有限元模型计算结果进行对比分析。不同本构模型的力学计算参数见表3。

表3 力学计算参数

除了橡胶本构模型的选取，为分析有限元模型中弹性密封垫两端位移约束条件对计算结果的影响，分别设置弹性密封垫两端约束条件为：①固定密封垫两端表面的轴向位移为0；②密封垫两端表面自由变形，无轴向位移约束。

考虑密封垫本构模型的选取和边界条件的不同，对每种密封垫分别进行4 次模拟：①采用Mooney‐Rivlin 模型，两端有位移约束；②采用 Mooney‐Rivlin 模型，两端无位移约束；③采用Yeoh模型，两端有位移约束；④采用Yeoh模型，两端无位移约束。

4 结果分析与讨论

4.1 密封垫变形

两种密封垫在错台量为0 mm 以及在两端存在位移约束的情况下，张开量为8 mm 和0时采用不同本构模型的密封垫变形见图5和图6。

图5 密封垫5两端存在位移约束下变形

图6 密封垫6两端存在位移约束下变形

由图 5 和图 6，对比 Mooney‐Rivlin 本构模型和Yeoh 本构模型，两者对应的密封垫在不同张开量下的变形形态基本一致。压缩至最小张开量时，两种密封垫均能很好地填充管片沟槽内的空间。

4.2 数值模拟与室内试验误差

为进一步分析不同橡胶本构模型、密封垫两端有无位移约束条件下密封垫装配力的差别和变化特点，绘制其压缩量-装配力曲线，见图7。

图7 不同密封垫的压缩量-装配力曲线

根据装配力大小和装配力增长速率的变化特征可以将密封垫的压缩过程分为三个阶段：①在阶段Ⅰ，压缩量从0增加至装配力增长速率出现大幅下降，这一阶段内密封垫变形程度较小；②在阶段Ⅱ，随着压缩量的增加，装配力大小缓慢增加甚至出现减小的现象；③阶段Ⅲ为压缩量继续增加至最大值时，此阶段内随着压缩量的增加，装配力快速增加并且增加得越来越快。这是因为当压缩量较大时，密封垫的孔洞大部分已经被充填，并且橡胶作为几乎不可压缩的超弹性体材料，使得密封垫的压缩难度增大，装配力快速增加。

提取密封垫在张开量为18、12、6、0 mm（对应压缩量分别为8、14、20、26 mm）时的装配力，见表4。

表4 密封垫在不同张开量下的最大装配力 kN·m-1

由图7 和表4 可知：对于密封垫5，室内试验的最大装配力59.7 kN/m，四种数值模型对应的最大装配力与试验数据的相对误差分别为17.4%、5.6%、80.4%、-17.6%。在与室内装配力模拟试验边界条件（两端有约束）相同的两种工况下，采用Mooney‐Rivlin本构模型的计算结果的相对误差仅为17.4%，而采用Yeoh 本构模型的计算结果相对误差则为80.4%，说明对于最大装配力而言，使用Mooney‐Rivlin 本构模型的计算结果更加准确。

同样采用Mooney‐Rivlin 本构的两种数值模型中，密封垫两端有约束比无约束情况下最大装配力大11.2%，而采用Yeoh 本构的数值模型中密封垫两端有约束比无约束情况下最大装配力大119.0%，说明边界条件的差异会对装配力模拟结果产生一定影响，这种影响在Yeoh 本构模型中更为显著。这是因为两端无约束工况下，密封垫两端会沿着密封垫轴向向外挤出，这样会使得相同压缩量下，未施加位移约束模型的装配力比施加位移约束模型小。

对于密封垫6，室内试验的最大装配力为64.2 kN/m，四种数值模型对应的最大装配力与试验数据的相对误差分别为4.7%、-18.9%、41.7%、-23.8%。在与室内装配力模拟试验中密封垫边界条件（两端有约束）相同的两种数值模型中，采用Mooney‐Rivlin 本构模型的计算结果的相对误差为4.7%，而采用Yeoh本构模型的计算结果相对误差则为41.7%，说明对于最大装配力而言，使用Mooney‐Rivlin 本构模型的计算结果更加准确。同样采用Mooney‐Rivlin 本构的两种数值模型中，密封垫两端有约束比无约束情况下最大装配力大29.1%，采用Yeoh本构的数值模型的这一值则为86.0%，说明边界条件的差异对装配力模拟结果的影响较为显著。

数值模拟装配力与试验数据的误差曲线见图8。可知，在密封垫压缩过程中阶段Ⅱ的装配力误差最小，其次是阶段Ⅰ，这两个阶段的最大装配力误差绝对值均小于8.0 kN/m，在阶段Ⅲ中装配力误差绝对值随压缩量的增加而不断增大。

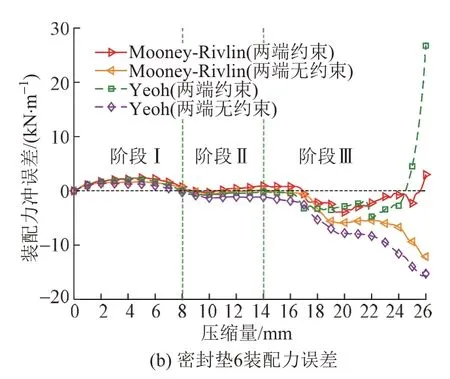
图8 两部密封垫数值模拟装配力与试验数据误差曲线

由上述分析可知，在与室内试验相对应的密封垫两端无约束的数值模型中，通常采用Mooney‐Rivlin 本构模型比Yeoh本构模型的装配力误差更小，前者更适合用来模拟分析本工程中三元乙丙炭黑填充橡胶密封垫在压缩过程中的力学行为。

5 结论

本文依托实际工程，针对两种截面形式的三元乙丙橡胶密封垫建立了一字缝处有限元模型，在对比室内试验结果的基础上，对橡胶本构和密封垫边界条件的选择展开分析。得到以下结论：

1）一般地，在与室内试验相对应的密封垫两端无约束的数值模型中，采用Mooney‐Rivlin 本构模型比Yeoh 本构模型的装配力误差更小，因此Mooney‐Rivlin本构模型更适用于三元乙丙炭黑填充橡胶密封垫在压缩过程中的力学行为。

2）密封垫两端边界条件的差异对计算结果有较大影响。本文中两种密封垫Mooney‐Rivlin 模型有约束比无约束情况下最大装配力平均大22.2%，Yeoh 模型有约束比无约束情况下最大装配力平均大97.9%。

3）密封垫压缩变形接近最大压缩量时，数值模拟结果与室内试验数据的误差绝对值随压缩量的增加而不断增大。对于最大装配力而言，使用Mooney‐Rivlin本构模型的计算结果更加准确。