基于概率匹配的栅格地图拼接算法

郝 奇，陈智君，郑 亮，陈 双，曹雏清

(1.哈尔滨工业大学芜湖机器人产业技术研究院，芜湖 241000；2.芜湖哈特机器人产业技术研究院有限公司，芜湖 241000)

0 引言

SLAM是现如今主流的地图构建方法，可以得到占据概率栅格地图，用于AGV导航，而栅格地图拼接是栅格地图扩展和多地图合并成大地图的一项关键技术。现有的地图拼接方法主要是基于图像的特征提取和匹配，如SIFT、SURF、ORB等，这些算法在彩色图像中的匹配效果很好，但是应用在栅格地图中的可靠性却很差，主要有两个方面原因：一方面是地图有很多局部相似的场景；另一方面是SLAM地图是基于一定区域范围的数据更新，使得很多栅格的概率和梯度值相同，最终导致栅格地图的特征和描述都非常相似[1-3]。

针对以上问题，本文提出了一个自适应分支定界匹配和双向概率残差优化的栅格地图拼接算法，并使用SLAM建立的栅格地图进行了拼接测试。

1 栅格地图匹配算法流程概述

算法流程如图1所示，首先读取源地图和目标地图，将地图像素的灰度值转化为占据概率，以概率阈值判别并提取占据点，得到源点云和目标点云；其次将目标点云和源地图进行自适应分支定界匹配，获取目标点云在源地图中的初始位姿；之后将目标点云通过初始位姿投影到源地图，构建概率残差的第一个约束，再将源点云通过初始位姿的逆变换投影到目标地图，构建概率残差的第二个约束；然后通过残差约束构建目标代价函数，进行非线性优化得到目标地图在源地图中的高精度位姿；最后通过优化后的位姿，将目标地图投影到源地图，通过概率融合得到最终的栅格地图。

图1 栅格地图拼接算法流程图

2 栅格地图的占据点云提取

如图2所示，读取两个栅格地图，分辨率为0.05 m，地图为8位单通道灰度图像。每个像素的灰度值value可以通过式(1)转化为[0,1]的占据概率，将大于阈值0.7的像素点判定为占据点，由此可以提取到两个占据点云，如图3所示。

图2 源地图和目标地图

图3 源点云和目标点云

probability=value/28

(1)

3 自适应分支定界匹配获取初值

理论上寻找目标点云在源地图中的初始位姿，需要遍历图像的每个像素位置和2π范围的姿态才能找到真正解，但该方法候选位姿数量太多，匹配速度过慢。因此本方法首先要对目标点云进行体素滤波减少点数，如图4所示。然后结合自适应分支定界方法大幅减少匹配候选项数目[4-8]。

图4 滤波后的目标点云

如图5所示，本方法使用多分辨率地图减少匹配候选项，以最低分辨率地图的所有位姿为根节点向下进行分支操作，图5只显示4个子节点位置，每个位置包含多个姿态。设定边界概率阈值，如果子节点概率得分大于阈值，继续向下进行分支搜索。父节点概率是用4个子节点中的最大概率进行表示，所以当父节点得分小于阈值时，可以进行剪枝操作，放弃其下的所有子节点，这样就能大幅减少匹配位姿的候选项，大幅提高匹配效率。

图5 分支定界结构图

首先计算自适应分支定界参数，已知源地图的宽和高分别为Width和Height，最高分辨率地图的分辨率为1个栅格，每低一层，地图的分辨率为上一层的2倍。为避免最低分辨率地图的候选项数目过少，因此在每个方向上取不少于K个候选项，即可得到如下公式计算分支定界的总层数L：

(2)

式中，min是取较小值函数；floor是向下取整函数。

那么第n层的匹配位置候选项目Num_tn为：

Num_tn=Width×Height/4L-1,n∈[1,L]

(3)

已知第n层地图分辨率Rn=2n-1，由余弦定理计算第n层的角度步进值Angn：

(4)

最终得到第n层的总匹配候选项数目Numn：

Numn=Num_tn×2π/Angn

(5)

经过对源地图进行计算，分支定界自适应总层数为7，如图6所示，黑色为自由区域，白色为占据区域，分辨率越低，白色区域越大，符合上述父节点概率是4个子位置节点中最大概率的表述。

图6 分支定界多分辨率地图

经过多分辨率地图匹配，目标点云可以在地图上找到最大得分候选项的子节点位姿pt，即是目标点云在源地图中自适应分支定界匹配的最佳位姿。

4 非线性优化获取高精位姿

4.1 构建优化目标函数及高斯牛顿优化

位姿pt的位置和真实最优位置有大约1个栅格分辨率的偏差，因此还需要进行非线性优化找到最优位姿。非线性优化方法很多，本方法选用较为广泛使用的高斯牛顿方法去优化，迭代速度较快，全局收敛较为精准稳定[9-11]。具体计算过程如下：

首先通过残差确定非线性最小二乘目标函数F：

F=∑[1-MS(GS(pT))]2+
∑[1-MT(GT(pT-1))]2→0

(6)

式中，函数M表示点在栅格地图的双三次插值概率，下标S和T分别代表源和目标；函数G表示点的栅格坐标；pT为目标点云的非线性优化位姿，其初值为pt，那么源点云在目标地图中的位姿为pT-1。

首先对目标函数在初值pt处进行一阶泰勒展开：

F=∑[1-MS(GS(pt))-MSGSΔδ]2+
∑[1-MT(GT(pt-1))-MTGT(pt-1)Δδ]2

(7)

式中，Δδ是位姿增量；M是地图概率对栅格坐标的雅各比矩阵；G是栅格坐标对位姿的雅可比矩阵。

对Δδ求导，化简可得：

∑[MSGS(pt)]T[1-MS(GS(pt))-MSGS(pt)Δδ]+
∑[MTGT(pt-1)]T[1-MT(GT(pt-1))-MTGT(pt-1)Δδ]=0

(8)

令MS=1-MS(GS(pt))；MT=1-MT(GT(pt-1))。

移项并提取Δδ整理可得：

∑(MSGS(pt))TMSGS(pt)Δδ+
∑(MTGT(pt-1))TMTGT(pt-1)Δδ=
∑(MSGS(pt))T[1-MS]+
∑[MTGT(pt-1)T[1-MT]

(9)

令HS=(MSGS(pt))T(MSGS(pt))；HT=[MTGT(pt-1)]T[MTGT(pt-1)]；KS=(MSGS)T[1-MS(GS(pt))]；KT=[MTGT(pt-1)]T[1-MT(GT(pt-1))]。

可得非线性优化的位姿增量Δδ：

Δδ=(HS+HT)-1×{KS+KT}

(10)

因此需要求解6个元素，分别是地图插值概率MS和MT、概率地图的雅各比矩阵MS和MT、栅格坐标对位姿pt的雅各比矩阵GS(pt)和GT(pt-1)，即可得到位姿增量Δδ。

4.2 求解概率地图的雅可比矩阵

栅格概率是离散的，直接使用栅格概率会限制后续优化的精度。因此将单栅格概率看作周围16个栅格连续分布的一个样本，如图7所示，此时插值获得的概率更精准，也能实现对位姿求导[12-14]。

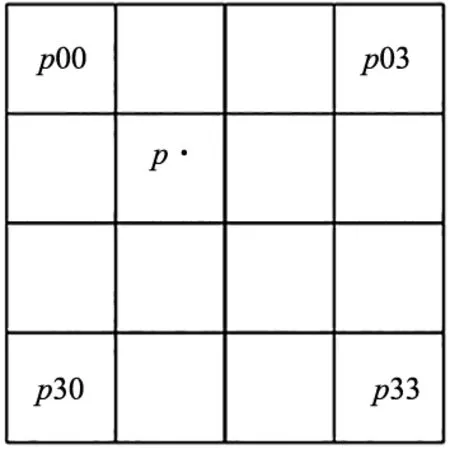
图7 概率地图插值

三次插值函数f如下：

f=ax3+bx2+cx+d

(11)

如图7所示，以点云的一点p为原点，通过单一维度上4个栅格横坐标(-1,0,1,2)对应4个概率值(p0,p1,p2,p3)，代入函数f，可得三次多项式系数：

(12)

那么插值函数对于当前维度变量的导数为：

f=3ax2+2bx+c

(13)

式中，p的浮点栅格坐标为(r,c)，向下取整坐标为(row,col)，取小数部分坐标为(u,v)。

将4行数据和自变量v值第一次代入插值函数可得4个行插值结果fr和4个对c的偏导fc：

(14)

将fr和u值代入插值和求导函数分别得到栅格数据的总插值结果M和对r的偏导dMr，M即是式(7)的M(G)，对应位姿pt和pt-1分别是MS和MT。

M=[dMrdMc]

(15)

即可得到位姿pt和pt-1对应的概率地图雅可比矩阵分别是MS和MT。

4.3 求解栅格坐标的雅可比矩阵

经过自适应分支定界匹配，可以得到初始位姿pt=(tx,ty,θ)T，那么由逆变换可得pt-1：

(16)

将点pi经过位姿pt和pt-1进行旋转平移变换，再代入函数G分别可得栅格坐标GS(pt)和GT(pt-1)：

(17)

对机器人位姿pt(tx,ty,tθ)求偏导，分别可得雅可比矩阵G(pt)和GT(pt-1)：

(18)

此时式(10)的所有元素值已经求出，通过迭代求解Δδ，设定增量阈值，当迭代步进值小于阈值，迭代停止，得到非线性优化位姿pT=pt+Δδ。

5 占据栅格地图的概率融合

已知目标地图在源地图中的最优位姿，通过坐标转换得到每一个像素点在源地图中的像素坐标，读取并转化为概率值prob_s，此时已知目标点像素概率值为prob_t，那么可以通过下式融合概率[15-16]：

首先计算两者占据概率值的赢率：

(19)

那么可以得到融合赢率odds=oddss×oddst，通过如下公式转换为占据概率Prob：

(20)

融合后的占据概率值通过式(1)再转回像素的灰度值，最终得到拼接后的栅格地图。

6 栅格地图匹配实验

6.1 基于图像的特征匹配实验

现有的地图拼接方法主要是基于图像的特征匹配，这些算法在彩色图像中匹配效果很好，但是在SLAM地图中却很差，图8是基于ORB的特征匹配结果，选取30组最优特征对进行显示。

图8 基于ORB的特征提取和匹配

源地图和目标地图的多个房间都非常相似，导致局部特征的相似，但在地图拼接不能因为局部特征的相似却忽略全局的匹配度，所以使用图像特征不可靠。此外栅格地图为SLAM构建的灰度图，其基于区域的概率更新特性使得大多数栅格的概率和梯度相同，使得特征匹配的可靠性比较差，容易出现误匹配和地图拼接失败。

6.2 自适应分支定界匹配实验

结果如表1所示，源地图提取的占据点云点数为8892，目标点云的点数为10 855，体素滤波后保留了101个点，通过滤波后的目标点云和源地图进行自适应分支定界匹配，匹配过程耗时1.732 s，找到最高概率得分0.565 339对应的最优节点位姿，最终得到目标点云在最高分辨地图中的匹配位姿pt。

将目标地图的非未知区域，即对白像素点和黑像素点通过位姿pt进行坐标变换，投影到源地图，概率融合即可得到拼接后的地图，如图9a所示。基于图像特征匹配直接使用最优30组特征对，但匹配结果仍然不可靠，因此人工选取真实对应的特征对进行拼接，结果如图9b～图9d所示，ORB优于SIFT和SURF，但拼接图右侧仍然有不重合，自适应分支定界匹配拼接是完全重合的，说明在栅格地图匹配中，本实验方法比基于图像特征匹配拼接的效果更好。

(a) 自适应分支定界匹配拼接结果 (b) ORB匹配拼接结果

(c) SIFT匹配拼接结果 (d) SURF匹配拼接结果图9 拼接图对比

通过匹配位姿将目标地图投影到源地图，统计重合的占据栅格数N，将所有重合占据栅格概率差值的和除以N，记作均值残差PS，作为评价拼接精度的指标，均值残差越小，表明匹配精度越高。

实验结果对比如表1所示。4种方法的匹配位姿都相近，由重合占据栅格数和均值残差来看，ORB的重合栅格数多于SIFT和SURF，均值残差也较小，说明ORB的精度更高。当ORB和自适应分支定界对比，看似ORB耗时较少，实则易出现误匹配，且需要人工选取匹配特征对，所以真实耗时更多，而自适应分支定界无需人工选取特征对的二次操作，而且匹配的重合占据栅格数明显更多，均值残差明显较小，说明自适应分支定界的匹配精度更高。

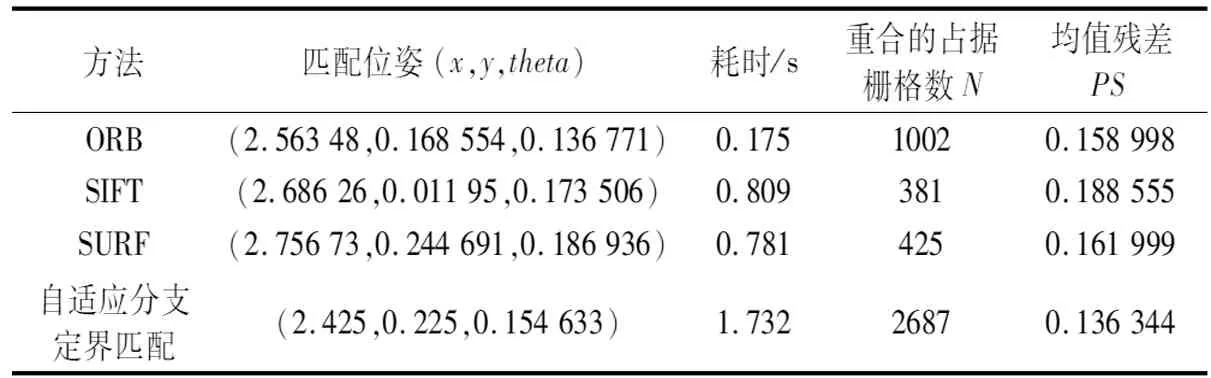
表1 匹配结果对比

6.3 基于双残差约束的非线性优化实验

如图10所示，非线性优化结果和图9a比较相似，由表2可知的匹配位姿可知，两者只有不到一个栅格的位置差。经过非线性优化，目标地图和源地图的占据重合点数由2687增长到2934，均值概率残差由0.136 344降低至0.127 698，说明基于双残差约束的非线性优化在自适应分支定界基础上，进一步提高了匹配重合度和匹配精度。

图10 非线性优化后的地图拼接结果

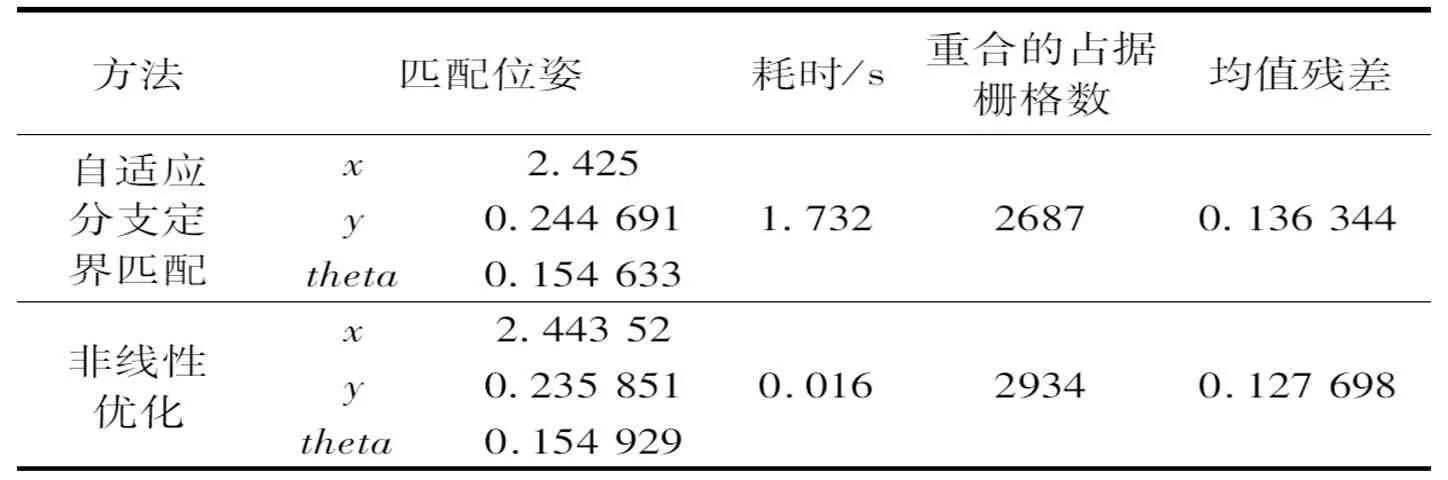
表2 匹配结果对比

在耗时上，非线性优化用时约0.016 s，速度比特征提取匹配和自适应分支定界匹配都要快，自适应分支定界和非线性优化总耗时约1.748 s，满足工业场景的地图拼接任务需求。

6.4 多环境地图的拼接实验

为了试验算法的通用性，实验选取多个环境的地图进行了拼接测试，下面展示2组，其中环境A的两图重合度较小，相似环境特征较多，场景B两图姿态相差比较大，实验结果表明拼接算法都能快速有效地实现匹配拼接，说明该算法的可靠性能好，适用场景广泛，适用于多数环境的栅格地图拼接应用，对工业场景下的地图构建具有重要意义。

(a) 源地图和目标地图

(b) 拼接地图图11 场景A拼接地图

(a) 源地图和目标地图 (b) 拼接地图图12 场景B拼接地图

7 结论

本文提出了一种基于概率匹配的栅格地图拼接算法，该算法将地图拼接问题转化两个主要匹配问题：一是通过自适应分支定界匹配求解最大化占据概率的问题。该方法通过目标点云和多分辨率源地图的分支定界匹配，能高效稳定地找到匹配位姿，解决了栅格地图图像特征匹配可靠性差的问题；二是通过非线性优化求解双概率残差的最小二乘问题。非线性优化通过双概率残差构建最小二乘目标函数，通过高斯牛顿迭代寻找到目标地图在源地图中的高精位姿，解决了栅格地图匹配精度不高的问题。

经过实验测试，该算法的匹配效果好，迭代收敛速度快，匹配精度高，满足工业场景可靠性和精度的要求。