基于改进角度-时间谱分析的滚动轴承故障特征提取

汪鹏宇，丁云飞，鲁泓壮

(上海电机学院 电气学院，上海 201306)

滚动轴承在机械中应用非常广泛，一旦发生故障对整个设备的健康运行有很大影响，轴承的故障诊断是机械工程领域研究的重点之一[1-2]；然而现有方法大多只适用于恒速工况下获得的信号，无法解决变转速下滚动轴承故障特征提取问题[3-4]。

针对这一问题，学者们提出了基于阶比跟踪的旋转机械振动信号模型[5]，但其对角域再次采样时会造成信号的时域特征混乱，导致处理后的信号失真，因此相关学者开始探究新的方法：文献[6]提出循环谱分析，分析了变转速下故障信号的角域周期特性；文献[7]提出循环谱相关，通过对信号循环平稳性的二阶统计的描述进行旋转机械故障特征提取；文献[8]在提出角度时间确定(Generalized Angular-Temporal Deterministic, GATD)之后，进一步提出角度-时间谱(Angular-Temporal Spectrum, ATS)分析方法，分析了滚动轴承在变转速下振动信号具有的循环平稳特征，有效回避了阶比跟踪的缺陷。但变转速下滚动轴承振动信号成分复杂，通过ATS提取其故障特征时受干扰较大，无法准确提取其特征阶次。

本文提出一种用于提取变转速下轴承的故障特征的改进ATS分析方法，通过平均信息图优选信号中包含的故障信息频带，然后以此作为积分区间改进ATS，对特征提取效果进行优化。

1 角度-时间谱(ATS)

1.1 GATD信号

假设一变转速下原始信号为x(t)，对其进行标准化处理可得

(1)

式中：T为最大时间周期；φ0为初相位；m为回转次数；Φ为角周期；φ(t)为时间t对应的转角增量。

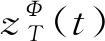
(2)

则认为x(t)符合GATD信号的相关特性，即为GATD信号。

信号的GATD特性用来描述变转速工况下在角域中表现出的周期性变换规律，但在时频域中可能不具有周期性变化规律的信号。滚动轴承作为最常见的旋转机械之一，其信号显然具有GATD特性。

1.2 ATS原理

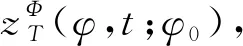
(3)

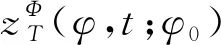
(4)

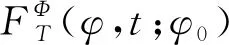
e-j2πΩφdφ，

(5)

式中：f为时域中的频率；Ω为频率在角域的表示(即阶次)；θ为最大角度周期。

由(5)式可知，影响ATS的主要参数是频率f和阶次Ω。由于没有优选频带，导致信号的ATS中含有大量无关信息，影响信号故障特征的提取。另外，由于更关注变转速信号的阶次信息，而频率等其他信息会影响阶次的清晰表达。沿谱频率轴对ATS进行集成运算可将其转化到二维平面，有效排除无关信息的干扰，并使信号特征更加突出，但积分频带的选取缺少科学依据，为此引入平均信息图解决此问题。

2 基于改进ATS的滚动轴承故障诊断

2.1 平均信息图

滚动轴承振动信号在某频带范围内的积分被定义为谱熵，谱熵负值定义为谱负熵。滚动轴承发生故障时会产生对应的脉冲信号，信号的变化会对其熵值产生较大的影响[9-10]，健康状态轴承信号的谱熵可以看作是一个常数，随着轴承故障严重程度的增加，轴承信号的谱熵逐渐减小，谱负熵逐渐增大。

对于长度为L的离散时域信号x(n),n=1,2,3,…，其在[f-Δf/2,f+Δf/2]频带上的谱负熵为

ESE(n;f,Δf)=|x(n;f,Δf)+jH(x(n;f,Δf))|2，

(6)

式中：H(·)为希尔伯特变换。

时域中的谱负熵定义为

ΔIe(f;Δf)=

(7)

式中：〈·〉为均值运算。谱负熵可被认为是时域中权重为ln(ESE(n;f,Δf)2/〈ESE(n;f,Δf)2〉)的谱峭度。

轴承局部故障可通过谱负熵ΔIE(f;Δf)描述为

(8)

式中：ESES(α;f,Δf)为频带[f-Δf/2,f+Δf/2]上的平方包络谱；α为循环频率；F(·)为傅里叶变换。

故障脉冲的出现会导致ΔIe(f;Δf)和ΔIE(f;Δf)均高于正常信号水平，但噪声等因素对二者的影响程度不尽相同。为解决这一问题，对ΔIe(f;Δf)和ΔIE(f;Δf)进行加权计算得到信号的加权谱负熵，即平均信息图，用于衡量信号的循环平稳特性和故障严重程度，计算公式为

(9)

2.2 轴承故障特征提取流程

在上述研究的基础上，基于改进ATS的滚动轴承故障特征提取方法如下：

1)对振动信号进行标准化处理，通过ATS分析生成SATS(Ω,f;φ0)。

2)应用平均信息图优选故障特征频带[f-Δf/2,f+Δf/2]，将其作为ATS的频率积分区间。

3)沿频率轴对ATS进行积分运算，得到改进ATS

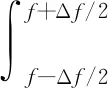
(10)

4)通过改进ATS分析识别信号的故障特征阶次，与滚动轴承故障特征的理论值进行对比判断故障类型。

3 试验验证

试验装置由驱动电动机、转速传感器、连接轴、联轴器、试验轴承(MB-ER-16K)和振动加速度传感器等组成，如图1所示[11]。试验选用Polytec激光测振仪获取轴承转速信号，转速传感器安装在连接轴上靠近电动机的一端以测量实时转速，使用Briiel & Kjaer4397加速度计采集故障振动信号，应用NI-USB-6211多功能卡完成数据储存与量化，试验轴承安装在连接轴上远离电动机的一端，基本参数见表1。

表1 MB-ER-16K型轴承基本参数

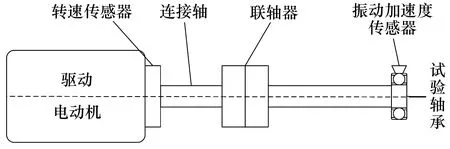
图1 试验装置示意图

用电火花分别在轴承外圈沟道、内圈沟道和钢球表面加工直径1.0 mm，深1.0 mm的圆坑模拟不同位置的故障。试验时，转速在频率20～25 Hz频段内均匀变换，振动信号的采样频率为12 kHz，采样时间为20 s。根据轴承参数得到外圈故障、内圈故障、钢球故障的特征阶次分别为4.099，5.901，2.684。

试验过程中，外圈故障轴承的转速信号和振动信号如图2所示。通过观察转速信号可以发现，轴承一直处于变转速状态，从原始信号的时域图中很难识别故障信息。

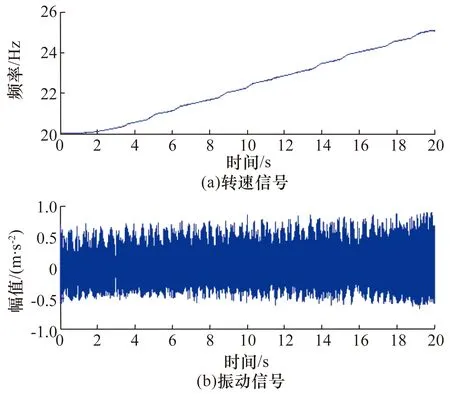
图2 外圈故障轴承的转速信号和振动信号

轴承外圈故障信号的ATS分析结果如图3所示，从中仅能隐约看出特征阶次(约为4.1)及少量转频信息(图中1,2,3,…)，难以清晰判断轴承是否故障。

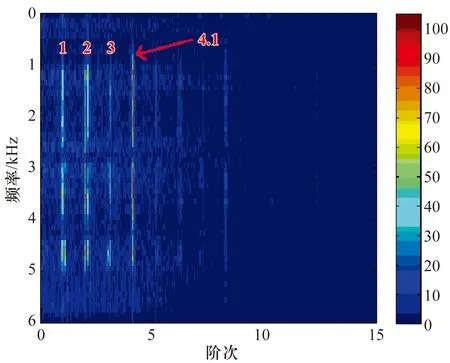
图3 外圈故障轴承振动信号的三维ATS

为选择最优积分频带，应用平均信息图处理信号的结果如图4所示：分解层数为3时，在以 3 375 Hz为中心、750 Hz带宽的频带内(图中画圈部分)，谱负熵值最大，所包含的故障特征信息最丰富。

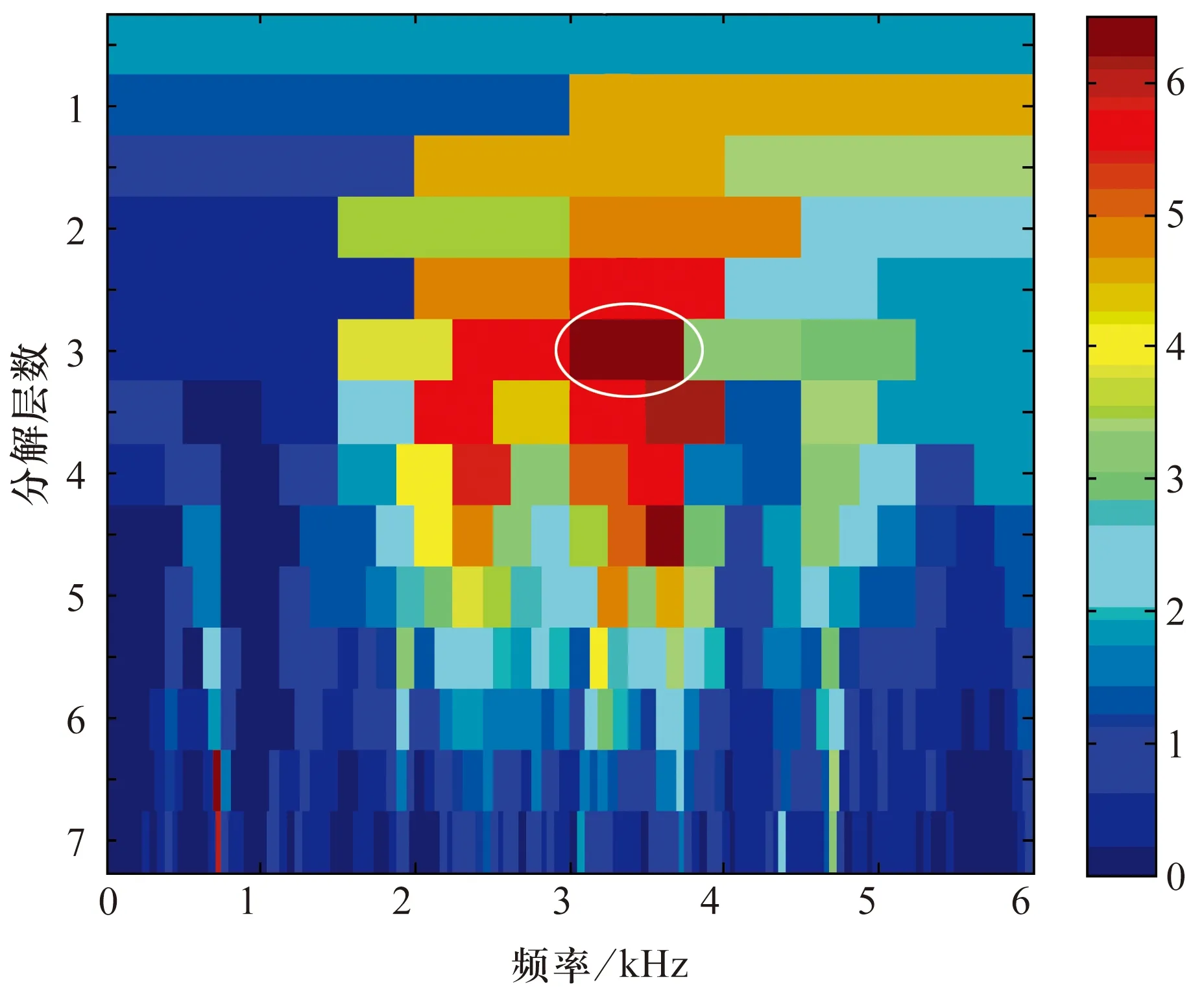
图4 外圈故障轴承振动信号的平均信息图

以[3 000，3 750] Hz作为积分区间，进一步计算信号的改进ATS，结果如图5所示：该信号的故障阶次与外圈故障特征阶次一致，可据此判断其故障类型为外圈故障。

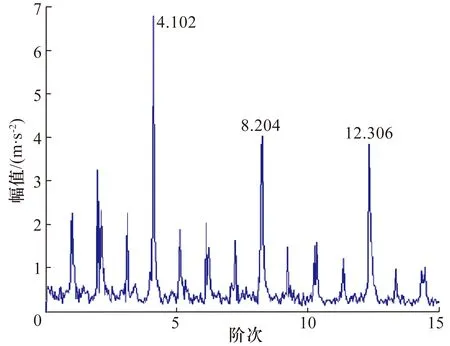
图5 外圈故障轴承振动信号的改进ATS

应用改进ATS分析方法分别对正常、内圈故障、钢球故障的轴承振动信号进行分析，结果如图6所示：图6a中只有正常轴承对应的转频阶次，未见故障阶次，说明该轴承处于健康状态；而在图6b和图6c中，除去图6a所示正常轴承对应的转频阶次外可以清晰地识别出故障阶次及其倍频，分别与理论计算的内圈和钢球故障阶次及其倍频相吻合。

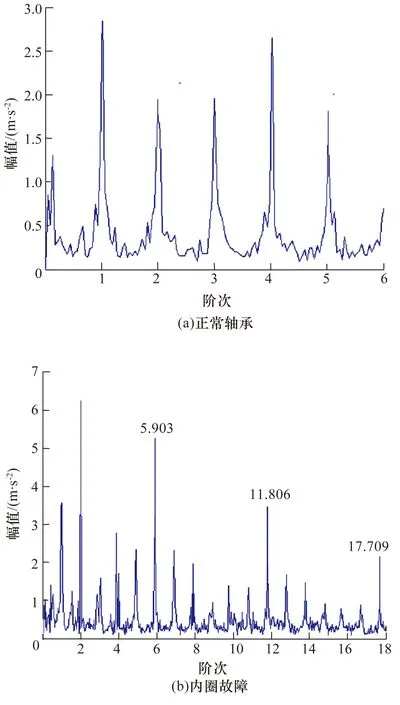
图6 不同状态下轴承振动信号的改进ATS

综上可知，改进ATS通过优选故障特征频带，然后对谱频率轴进行积分运算提高了三维ATS的应用效果，能够准确反映轴承的故障阶次并提取故障特征。

采用阶比跟踪方法对轴承振动信号进行处理，对信号进行重采样后结果如图7所示：较之改进ATS分析，重采样后的包络谱信号故障特征不清晰，信号的时域特征出现混乱，无法准确提取轴承故障特征。进一步证明了改进ATS分析在变转速下轴承振动信号故障特征提取方面的优越性。

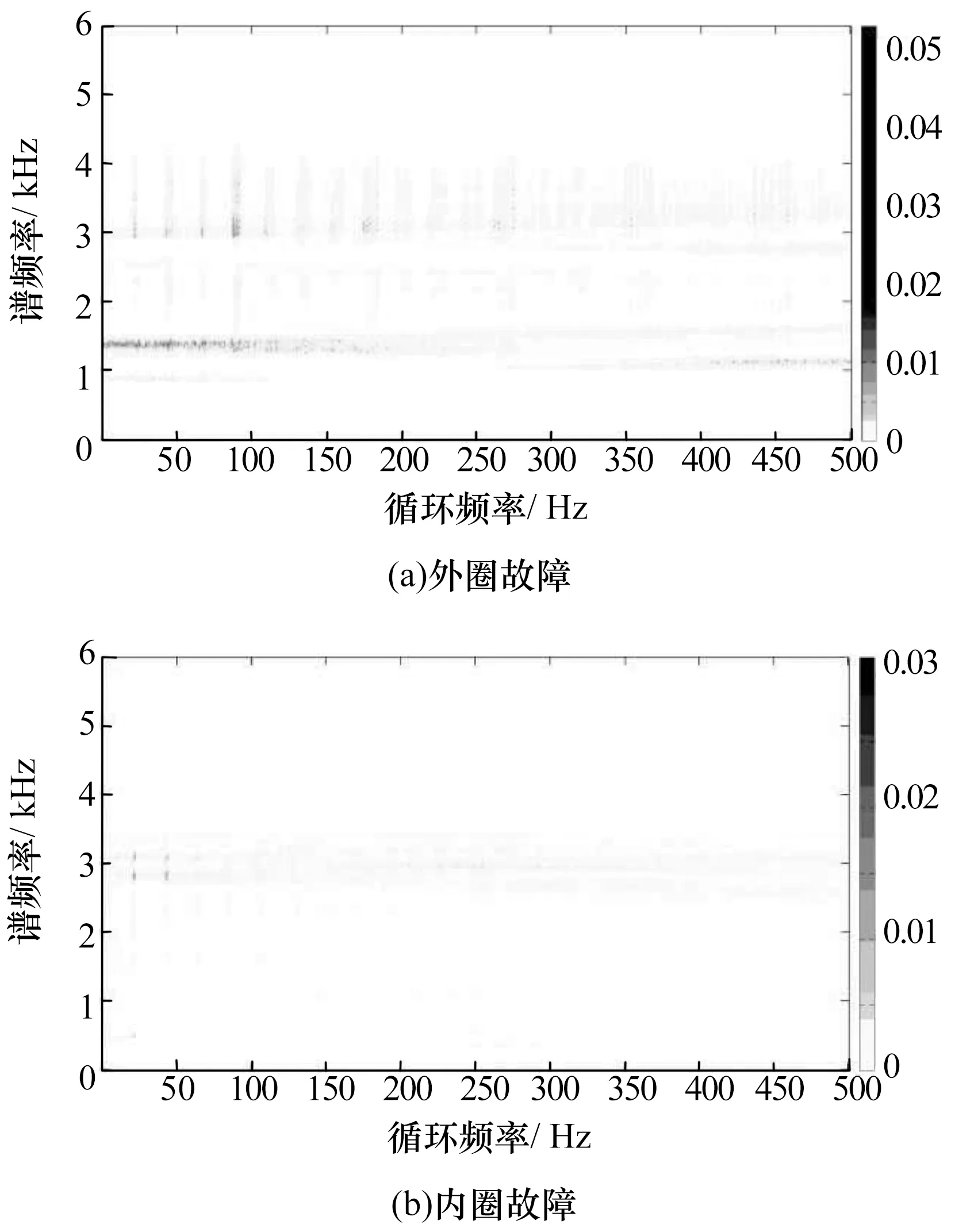
图7 3种轴承故障信号的包络谱图

4 结论

针对ATS难以提取故障特征的问题，提出了改进ATS分析方法。引入平均信息图优选信号的共振频带，通过集成运算将三维ATS转化到二维平面内，并采集轴承故障信号对改进ATS谱的应用效果进行验证。主要得到以下结论：

1)ATS可用于分析变转速下旋转机械故障信号，但在提取故障阶次时会发生谱图模糊的现象。

2)平均信息图以谱负熵为依据反映信号在不同频带内的脉冲特性，能够优选信号中故障特征最丰富的频带。

3)与ATS相比，选择最佳频带范围进行积分运算得到的改进ATS，在变转速下提取轴承故障信号有较为明显的优势，有助于准确提取故障特征。