滑动轴承中不规则表面微结构对空穴现象的影响
覃哲,邹爱成
(桂林航天工业学院 机电工程学院,广西 桂林 541004)
轴颈中心与轴承中心不同轴时,轴颈与轴承之间微小的环形间隙会被来自孔和槽供应的润滑油膜填充。在旋转轴颈的驱动下油膜通过轴承与轴颈所形成的楔形间隙,当油膜经过最小间隙后轴承与轴颈之间的间隙会逐渐增大,油膜压力也会下降[1]。油膜压力下降到低于释放油膜所溶解气体的饱和压力后,溶解在油膜中的气体会分离出来产生气泡,从而导致轴颈与轴承之间的间隙出现空穴,造成轴承的过早损坏[2-3]。鉴于表面微结构技术在提高摩擦副润滑和摩擦性能方面的应用价值[4-8],通过改进轴承表面微结构来减少甚至消除轴承的空穴现象成为可能。
关于表面微结构和空穴现象的研究:文献[9]研究了方形织构引起的气穴效应对摩擦副润滑性能的影响,发现当织构深度接近油膜厚度时在引起气蚀和促进润滑方面的效果最佳;文献[10]在稳态条件下研究了具有圆凹坑织构推力轴承中的气穴现象,发现圆凹坑织构中的气蚀与轴承旋转速度有关;文献[11]通过研究推力轴承中的气穴现象,发现空化形状和面积与轴承表面纹理图案有关;文献[12]基于控制体积质量守恒原理分析了倾斜轴颈轴承宏观空穴和微凸体间空穴对润滑性能的影响,研究发现在空穴区域润滑介质密度低,空穴较大;文献[13]研究发现流体润滑条件下摩擦副表面微凸体织构的宽度或高度、微织构前端和后端的角度均能导致空化区域面积增加。
上述研究的重点均是表面织构(表面具有一定规则的三维形貌)对空穴现象的影响,但缺乏不规则表面微结构对空穴现象影响的研究。本文提出一种研究不规则表面微结构对轴承空穴现象影响的新方法。首先,由编辑的MATLAB程序生成轴承曲面的点云数据;然后,基于生成的点云数据采用逆向成形的方式重构出带不规则表面微结构的轴承曲面,利用重构的轴承曲面及COMSOL Multiphysics中“CFD模块”提供的“薄膜流体,壳”接口,通过求解狭窄结构的流体雷诺方程模拟轴承中的油膜流动;最后,得出润滑油膜空穴区域及油膜的压力分布。以带有不规则表面微结构的滑动轴承为对象,研究深度为1~40 μm的不规则表面微结构对轴承空穴现象的影响。
1 不规则表面微结构的滑动轴承模型
具有不规则表面微结构的滑动轴承模型如图1所示,为便于说明,适当放大图中不规则表面微结构尺寸。滑动轴承宽度B=50 mm,轴瓦半径R=24.95 mm,轴颈半径r=24.90 mm,Δh为不规则表面微结构深度,取轴颈中心O为极点,轴承中心为O1,OO1为极轴,h为任意角度φ的油膜厚度,h0为油膜压力最大处的油膜厚度,φ0为极轴OO1旋转到油膜压力最大处的角度,e为偏心距,F为轴承的外载荷,n为轴颈转速。
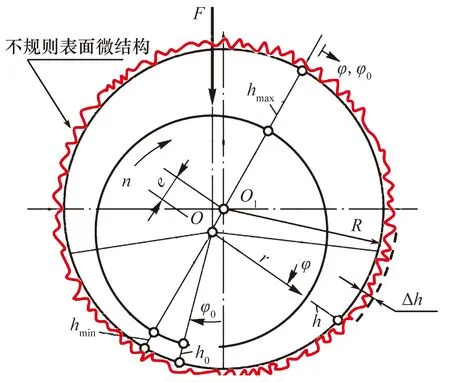
图1 具有不规则表面微结构滑动轴承的二维示意图
采用逆向成形的方式构建具有不规则表面微结构的滑动轴承模型,步骤如下:
1)点云数据生成阶段。借助MATLAB编写程序生成滑动轴承曲面的点云数据,核心代码为
θ=linspace(0,360,1080);
R=24.95;
X=[];
Y=[];
Z=[];
for n=-25:0.145:25
r=R+△h×rand(1,1080);
X=[X,r×cosd(θ)];
Y=[Y,r×sind(θ)];
Z=[Z,n×ones(1,1080)];
end
编程思路如图2所示,沿轴承轴向假想将需要逆向成形的轴承曲面细分成345个点圈,相邻点圈之间的距离均为0.145 mm,每个点圈由均匀分布的1 080个点组成,借助这372 600个三维空间数据点,模拟生成滑动轴承的整个曲面,轴承的表面积S=2πRB=7 838.04 mm2,其中每1 mm2的轴承曲面均由48个空间数据点通过逆向成形产生。

图2 逆向成形生成点云数据
2)点云及多边形处理阶段。包括点云数据优化、网格优化、修复孔和凸起,目的是创建出高质量面片数据。
3)领域划分阶段。主要根据三维空间数据的曲率和特征,将面片数据拟合为不同的几何领域。
4)精确曲面阶段。提取轮廓曲线,构建曲面片网格,移动面片组,布尔运算与曲面裁剪,拟合曲面。
借助三维软件SolidWorks中的ScanTo3D插件,最终以逆向成形的方式,将程序生成的点云数据分别构建出9个表面微结构深度不等的滑动轴承曲面模型,这些轴承曲面中不规则表面微结构深度Δh分别为1,5,10,15,20,25,30,35,40 μm,模型如图3所示。

图3 依据点云数据生成的滑动轴承曲面
2 基本控制方程
为模拟润滑油膜在轴承与轴颈间的流动,采用COMSOL Multiphysics中“CFD模块”提供的“薄膜流动,壳”接口。“薄膜流动,壳”接口用于求解狭窄结构的流体雷诺方程,并使用薄层结构厚度上的平均流函数表示质量和动量平衡。边界条件作为准确求解雷诺方程的关键,COMSOL Multiphysics中采用文献[14-15]修正后的数值算法实现JFO边界条件,该边界条件可以提供油膜破裂条件,并在油膜重新形成处满足质量守恒定律[10]。
“薄膜流动,壳”接口使用雷诺方程的一般形式求解气态空穴的产生区域,雷诺方程为
(1)
h=rψ(1+εcosφ),
式中:p为油膜压力;η为润滑油动力黏度,取0.036 Pa·s;v为轴颈圆周速度;ψ为轴承的相对间隙(滑动轴承直径间隙与轴颈直径之比);ε为偏心率;∂p/∂x=0时,h=h0。
针对空穴区域的求解,“薄膜流动,壳”接口在所使用的雷诺方程中引入一个与p和空化过渡宽度Δpsw有关的内置开关函数g=f(p,Δpsw),Δpsw=1 MPa。在非空穴区域开关函数g的值等于1,在空穴区域开关函数g的值等于0。开关函数g支持对空穴区域和非空穴区域单独求解雷诺方程,结合连续性方程修正(1)式中的v,即
(2)
式中:vc,vp分别为油膜的平均库埃特流速度和平均泊肃叶流速度,空穴区域的vp设为0;ρ为油膜密度。
设置轴承的外载荷为15 000 N,轴颈转速为10 000 r/min,求解得到轴承的相对间隙ψ=0.003 5,轴承的承载量系数cp=1.957 5,通过插值法得到偏心率ε=0.702。将轴承构建的曲面模型导入COMSOL Multiphysics,借助“薄膜流动,壳”接口对工作中的润滑油膜进行仿真运算,油膜的压力分布及油膜所产生的空穴区域均可求出。
3 计算结果与分析
3.1 表面微结构深度对油膜流速的影响
不规则表面微结构深度不同时滑动轴承曲面相应的润滑油膜流速如图4所示:润滑油膜的低流速区与高流速区之间是轴颈与轴承所形成的楔形空间,此处的油膜压力与外载荷平衡;随着不规则表面微结构深度Δh的增大,低流速区油膜的整体流速逐渐降低,从9~11 m/s降到4~6 m/s,而高流速区油膜的整体流速逐渐升高,从15~16 m/s升到18~21 m/s。因此,增大不规则表面微结构的深度,在轴承所形成的楔形空间两侧,润滑油膜的流速差也在增大。

图4 不规则表面微结构深度不同时滑动轴承润滑油膜的流速
3.2 表面微结构深度对油膜压力的影响
不规则表面微结构深度不同时滑动轴承曲面相应的润滑油膜压力分布如图5所示:当不规则表面微结构的深度Δh≤10 μm时,与外载荷平衡的油膜压力p为4~11 MPa;随着Δh的不断增大,p不断增大,当Δh增大到40 μm时,p增大到8~19 MPa。
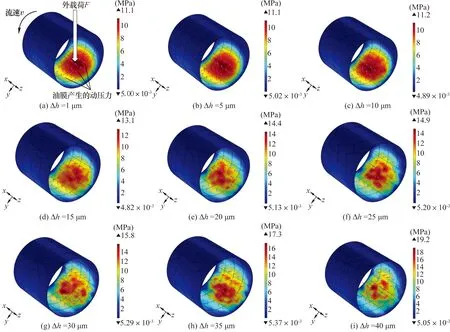
图5 不规则表面微结构深度不同时滑动轴承润滑油膜压力分布
3.3 表面微结构深度对油膜空穴区域的影响
不规则表面微结构深度不同时滑动轴承曲面相应的润滑油膜的流体质量分数ω的分布如图6所示。
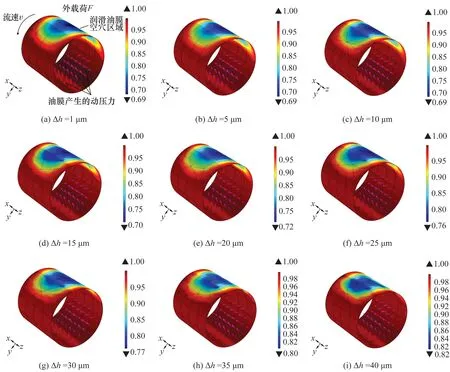
图6 不规则表面微结构深度不同时滑动轴承润滑油膜的流体质量分数
润滑油膜中产生的空穴现象通过油膜的流体质量分数ω反映,轴承工作过程中:油膜非空穴区域的压力大于空气分离压,溶解在油膜中的气体没有从油膜中分离出来,非空穴区域内油膜ω=1;空穴区域(该区域只有部分体积为流体)的压力小于空气分离压,溶解的气体以很高的速度分解出来,成为游离微小气泡并聚合长大,空穴区域内油膜ω<1。故油膜ω<1的区域越大,空穴区域越大;空穴区域内油膜ω越小,油膜的空穴现象越明显。
通过分析图6可知,若不规则表面微结构的深度Δh≤10 μm,改变表面微结构深度Δh时,油膜ω<1的区域基本不受影响,空穴区域内油膜ω在[0.68,1)之间;随着深度Δh从10 μm不断增大到40 μm,空穴区域内油膜ω逐渐增大:可见一定范围内增大不规则表面微结构的深度可以减少油膜中产生的空穴现象。
4 结束语
通过求解狭窄结构的流体雷诺方程来模拟轴承中的油膜流动,研究深度为1~40 μm的不规则表面微结构对滑动轴承空穴现象的影响,研究发现在等转速、等载荷的工况下,将轴承中不规则表面微结构的深度从1 μm增大到40 μm,轴承楔形空间两侧油膜的流速差、与外载荷平衡的油膜压力p、空穴区域内油膜的流体质量分数ω均不断增大,轴承油膜中产生的空穴现象逐渐减少。

