极寒大温差环境下温度对轴承配合的影响及自适应补偿结构

唐术锋，王旭，张慧杰，姚佳男，程曦

(1.内蒙古工业大学 机械工程学院，呼和浩特 010051；2.内蒙古自治区特殊服役智能机器人重点实验室，呼和浩特 010051)

在极地、高原科考以及深空探测等极寒大温差环境下，转动关节零件会发生变形，材料不同，变形不同，从而影响零件配合精度，甚至造成设备不能正常运转[1]。

国内外关于温度对机械零件配合精度的研究很多：文献 [2-3]分析了热误差对机械零件配合精度的影响，提出了机械热变形的补偿方法，分析了减少热误差的措施；文献[4]通过径向热变形试验分析了材料双层管间隙热变形量的影响因素，得出材料双层管间隙的热变形量与材料种类和双层管内外径尺寸有关；文献[5]根据机械零件热变形和热膨胀规律提出了热误差补偿技术理论，通过该理论可减小零件配合精度的变化。

上述研究采用温控技术、材料优化、热误差补偿等方法减小了温度对机械零件配合精度的影响，但大多需要复杂的系统。在此提出一种极寒大温差环境下消除热应力及热变形影响的自适应温差结构。

1 极寒大温差环境下轴承配合处应力及变形

以某极寒大温差环境(温度从22 ℃下降到-60 ℃)下旋转关节处紧配合的外壳与圆锥滚子轴承外圈(图1)为例分析，在极寒环境下将其视为刚性连接。外壳材料为硬铝合金，轴承外圈材料为GCr15，其主要结构参数见表1，材料参数见表2。为方便计算，根据几何特点将外壳和轴承外圈简化为厚壁圆筒[6]。

图1 外壳与轴承外圈配合示意图

表1 外壳与轴承外圈主要结构参数

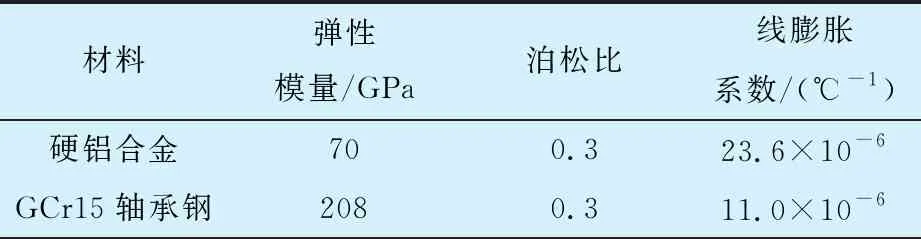
表2 外壳与轴承外圈材料参数

1.1 理论分析

同一变化的温度场中，2个紧配合的零件由于热膨胀系数不同，变形不同，无法自由胀缩，从而产生不同的热应力。

基于弹性力学和传热学理论可得外壳A与轴承外圈B的热变形uA，uB，可表示为

(1)

式中：αA，αB分别为外壳、轴承外圈的线膨胀系数；rAI，rAO分别为外壳的内、外半径；rBI，rBO分别为轴承外圈的内、外半径；TA(r)，TB(r)分别为外壳、轴承外圈沿半径方向的温度[7]。

同一温度场中外壳与轴承外圈温度变化相同，则(1)式也可表示为

(2)

式中：ΔT为温度变化量。

外壳与轴承外圈在极寒大温差环境下的变形如图2所示。在初始温度为22 ℃时，轴承外圈内外表面分别在a,b点所在弧面，外壳内外表面分别在b,c点所在弧面,配合面为b点所在弧面。当外界温度下降到-60 ℃时，外壳与轴承外圈自由收缩。若两者之间无相互约束，由(2)式可得uA=0.045 477 mm，uB=0.021 195 mm。外壳内表面由b缩小至m所在弧面，轴承外圈外表面由b缩小至n点所在弧面。由于2个零件在配合面固定，径向与周向不能相对移动，约束作用使外壳实际收缩量小于自由收缩值，外圈实际收缩量大于自由收缩值。

图2 外壳与轴承外圈的热变形示意图

热胀冷缩作用下相互约束的零件在径向平面上会同时受径向与周向弹性应力的作用。因周向尺寸远大于径向尺寸，外壳与外圈在约束下收缩产生的热应力主要集中在周向。热应力使外壳周向方向伸长，轴承外圈周向方向缩短，如图3所示。

图3 外壳与轴承外圈周向尺寸变化示意图

在温度降低时，外壳在接触面处受周向弹性拉应力σA作用，从m点移至p1点所在弧面，轴承外圈受周向弹性压应力σB作用，从n点移至p2点所在弧面。p1，p2点所在弧面在应力作用下最终接触，即新的热稳态下外壳与轴承外圈配合面。

由胡克定律可知外壳的周向弹性应变为

εA=σA/EA，

(3)

外壳中径位置的周向伸长量为

εACAM=σACAM/EA，

(4)

CAM=(CAI+CAO)/2，

式中：EA为外壳弹性模量；CAM为外壳中径面圆弧周长；CAI，CAO分别为外壳内、外径面圆弧周长。

轴承外圈周向应变为

εB=σB/EB，

(5)

轴承外圈中径位置的周向伸长量为

εBCBM=σBCBM/EB，

(6)

CBM=(CBI+CBO)/2，

式中：EB为轴承外圈材料弹性模量；CBM为轴承外圈中径面圆弧周长；CBI，CBO分别为轴承外圈内、外径面圆弧周长。

外壳与轴承外圈周向尺寸沿径向由内至外线性增大，最终周向收缩量与周向长度正相关，采用中径处尺寸代替整体尺寸平均值。外壳周向收缩量为

αAΔTCAI-εACAM=αAΔTCAI-δACAM/EA，

(7)

轴承外圈周向收缩量为

αBΔTCBO-εBCBM=αBΔTCBO-δBCBM/EB，

(8)

式中：δA，δB分别为外壳、轴承外圈轴向长度。

由于外壳与轴承外圈刚性连接且保持原有形状，周向尺寸实际变化相同，即

Δlt=αAΔTCAI-δACAM/EA=

αBΔTCBI-δBCBM/EB。

(9)

当处于平衡状态时，配合面保持刚性接触，在周向剖面上外壳所受拉力与轴承外圈所受压力相等，即

σASA=-σBSB，

(10)

SA=(rAO-rAI)δA，

SB=(rBO-rBI)δB，

式中：SA，SB分别为外壳、轴承外圈截面面积。

由(9)，(10)式可得

(11)

(12)

周向收缩量与径向收缩量的关系为

CAI+Δlt=2π(rAI+Δlr)，

(13)

式中：Δlr为外壳和轴承外圈由于约束作用在接触面的径向位移。

由于温度变化，轴承外圈自身也会沿径向收缩，轴承外圈在极寒大温差环境下的径向位移为

ΔlBI=Δlr-(rBO-rBI)αBΔT。

(14)

外壳和轴承外圈的应变为

(15)

1.2 有限元分析

1.2.1 建模

根据表1和表2的数据建模并导入ANSYS Workbench，采用扫掠法进行网格划分，由于热应力产生的弹性应变相对整体尺寸较小，在此选用0.8 mm的网格。划分后有限元节点数为608 943，单元数为140 625。

1.2.2 变温过程模拟

施加温度场：初始温度设置为22 ℃，共设置4个载荷步，载荷步长为1 s，第1步温度下降22 ℃，其余载荷步温度降低20 ℃。

外壳与轴承外圈的接触面会向3个方向产生变形，在降温过程中2个零件周向与径向始终保持接触，在过盈配合下轴向会受到限制而不能自由变化，若用绑定接触(Bonded)限制轴向移动，仿真模型会由于泊松效应与边缘效应影响接触面的应力，在此选择无分离接触(No Separation)。仿真过程为了准确显示模型的应力与变形，不施加外载荷及约束条件。

1.3 结果分析

外壳与轴承外圈应力、应变与变形云图如图4所示，与理论计算的对比见表3，误差在允许范围之内，说明理论分析的正确性。

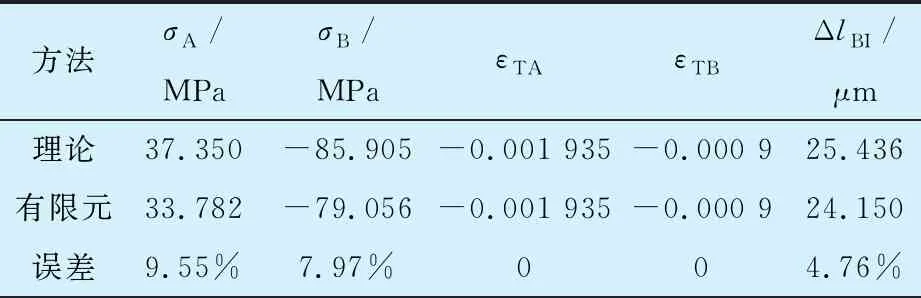
表3 外壳和轴承外圈应力、应变与变形的理论计算和有限元结果对比

图4 外壳与轴承外圈应力、应变与变形云图

分析可知：1)轴承外圈的径向位移ΔlBI(轴承径向游隙减少量)大于允许变化值(10～15 μm)，轴承内部摩擦力矩增大，在小游隙组的情况下轴承可能卡死；2)轴承外圈在径向受到89.042 MPa的正应力，反复的热应力会加剧零件疲劳，降低轴承使用寿命。为减小极寒大温差环境下温差对轴承配合的影响，改善转动关节的运动性能，提出一种可以减少配合零件在极寒大温差环境下尺寸变化的自适应结构，并保持轴向预紧力不变，使轴承游隙在一定范围内，从而提高运动精度并减少可能出现的摩擦力矩变化。

2 自适应结构

自适应结构如图5所示，在关节中的布置图如图6所示(β为套筒顶角，取76°)，功能实现原理如图7所示，温度变化时自适应结构可不断循环调整，直至进入热稳态。

图5 自适应结构图

图6 自适应结构在关节中的布置

图7 自适应结构功能实现原理图

自适应结构优点：1)外壳收缩受限而产生的热应力转化为斜向的压力，推动圆锥滚子轴承外圈向外侧移动，增大了外壳收缩所需的空间。同时，外圈向外侧的移动可以消除温度降低时轴承游隙的减小量。2)由于材料热膨胀系数差异，温度降低时套筒与外壳之间会产生间隙，利用弹簧压紧套筒使其通过球始终与外壳接触。3)套筒外侧为带有斜面的楔形圈，通过加载轴向弹力，使其达到径向定压预紧的效果，保证在大温差环境中径向载荷不变。

3 基于ADAMS仿真对结构有效性的验证

基于ADAMS建立运动学仿真模型，验证当温度从22 ℃下降到-60 ℃时，自适应结构将热效应产生的载荷转化为动力，促使轴承外圈向外移动，从而增大轴承径向游隙，消除因热应力导致的轴承径向游隙变化。

ADAMS无法模拟温变过程中物体的变形，故将热力耦合的复杂模型转化为运动学模型，将自适应结构中钢球径向位移量设定为外壳径向收缩量uA(0.045 477 mm)。如图8所示，建立自适应结构ADAMS运动学模型，内圈及滚子固定，外圈沿轴向移动。对所有钢球添加径向的移动副并施加位移驱动，由于瞬时的热应力极大，故采用STEP(time,0,0,8,0.045 477)函数控制运动时间及位移。在轴向添加刚度为200 N/mm的弹簧对外圈限位，防止模型由于约束不足一直运动。

图8 自适应结构ADAMS运动学模型

轴承外圈轴向位移计算结果如图9所示，最终位移量Δl为0.147 5 mm。当外圈向外侧移动后，与外壳和轴承外圈相连接的钢球会在凹槽内滚动并在新的位置维持平衡。由于轴承外圈背离外壳运动，径向位移增加量ΔlBI=Δl/tanβ=0.036 7 mm，大于极寒大温差环境下轴承外圈径向总变形(0.024 15 mm)，说明外壳在极寒大温差环境下收缩变形不受约束，热应力消失。新稳态时，在弹簧压力作用下轴承外圈与外壳重新达到刚性连接状态，维持了原有的游隙并消除热应力。

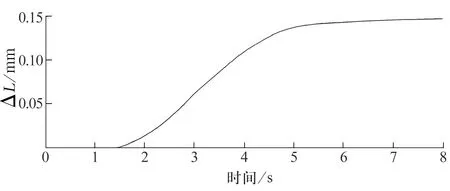
图9 轴承外圈轴向位移仿真结果

4 结束语

通过对极寒大温差环境下转动关节处外壳和圆锥滚子轴承外圈应力、应变及变形的分析，设计了一种温度自适应补偿机构，该机构通过轴向定压预紧，自动调节轴承径向游隙，避免低温下因配合间隙变小而产生的卡滞现象，提高了运动精度和传动效率。