助推学生高阶思维能力发展的信息化教学策略

【摘要】本文以人教版数学六年级上册“圆的面积”教学为例，探讨小学数学信息化教学助推学生高阶思维能力发展的策略，先是明确学习目标和能力发展目标，再基于目标达成设计教学框架、基于教学框架丰富教学内容，最后借助信息技术的应用发展学生的知识理解能力、新知探究与知识分析能力、新知应用与问题解决能力、创新性思维能力等高阶思维能力。

【关键词】高阶思维能力 信息化 教学策略

【中图分类号】G62 【文献标识码】A

【文章编号】0450-9889（2022）13-0074-03

按照世界著名未来学家阿尔文·托夫勒（Alvin Toffler）的观点，由信息革命引发的第三次浪潮大约始于20世纪50年代中期，其重要标志是计算机的发明与应用。关于信息化的概念，国内外学者一度众说纷纭。我国直至1997年召开首届全国信息化工作会议，才明确将信息化定义为“培育、发展以智能化工具为代表的新的生产力并使之造福于社会的历史过程”。中共中央办公厅、国务院办公厅在《2006—2020年国家信息化发展战略》中给信息化的定义是“充分利用信息技术，开发利用信息资源，促进信息交流和知识共享，提高经济增长质量，推动经济社会发展转型的历史进程”。将信息化的概念引入教学，指的是教师依托学校的智能化环境，利用信息技术的优势实施高品质教学的过程。

小学阶段是学生思维能力形成和发展的重要阶段，而学生思维能力的发展总是从低阶逐渐过渡到高阶。按照学界的说法，高阶思维能力是以高阶思维为核心解决劣构问题或复杂任务的一种心理特征，也可以说是一种发生在较高认知水平上的心智活动或较高层次的认知能力，具体可表现为知识理解能力、新知探究与知识分析能力、新知应用与问题解决能力、创新性思维能力等。

相对于其他学科来说，小学数学具有高度的抽象性，而小学生的思维特点则是以形象思维为主，将信息技术运用于小学数学教学，可有效提高数学知识的直观性、具象性，助推小学生高阶思维能力的发展、促进其对知识的理解与内化。下面笔者以人教版数学六年级上册第五单元第三节“圆的面积”教学为例，谈谈以信息化助推小学生高阶思维能力发展的策略。

一、基于教材和学情分析明确课堂学习目标及学生能力发展目标，构建驱动双目标实现特别是促进学生高阶思维能力发展的教学框架

以信息化助推小学生高阶思维能力的发展，在小学数学教学实践中，其逻辑起点是以学生能力发展为目标，構建信息化教学的整体框架。

在“圆的面积”一课中，经过教材和学情分析，笔者确定了如下4个难度递进的教学目标：（1）理解圆的面积的含义;（2）理解圆的面积计算公式的推导过程，感悟转化的数学思想;（3）能够运用圆的面积计算公式解决问题;（4）能够综合运用所学知识，进一步拓展知识应用与创新性解决问题的能力。重点是圆的面积的含义和圆的面积的推导过程，难点是圆的面积的推导过程。在4个教学目标中，与学生高阶思维能力相对应的能力目标依次是知识理解能力、新知探究与知识分析能力、新知应用与问题解决能力、创新性思维能力，且4个能力培养目标具有显著的进阶性特征。

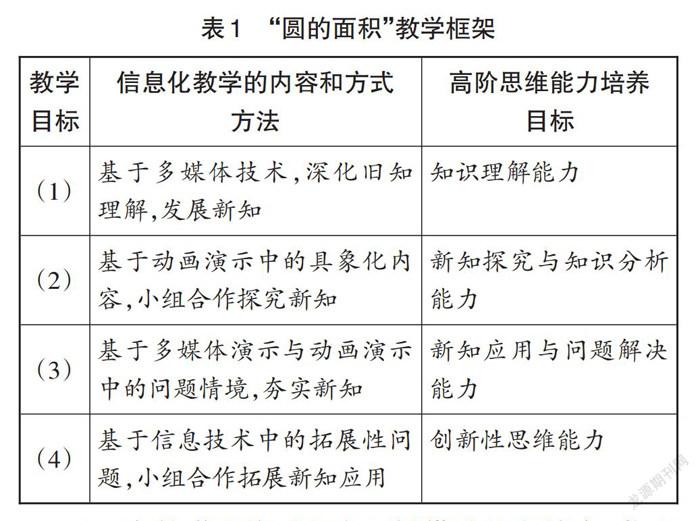
在笔者看来，信息化教学的方式方法从本质上来说是通过信息技术的应用提高教学内容的直观性、动态性，促进学生主动学习知识、探究知识的本质，从中获得相应水平的认知能力。而圆的面积计算公式的推导过程之所以是学生学习的难点，主要是因为它相对于其他学习目标来说具有一定的抽象性。为了帮助学生突破学习难点、达成学习目标，教师可以借助信息技术，选择适当的教学方式方法，将教学目标、信息化教学的方式方法和学生的高阶思维能力发展目标进行有效的对接。基于以上思考，笔者为“圆的面积”一课构建了如表1所示的教学框架。

二、在教学实施过程中巧妙借助信息技术，落实学生高阶思维能力发展目标

（一）借助信息技术的直观性，促进学生知识理解能力的发展

知识理解能力是学生运用旧知，在分析新知的基础上，对新知进行理解的能力。知识理解有三级水平：低级水平的知识理解是知觉水平的理解，即能辨认和识别对象，并且能对对象命名，知道它“是什么”;中级水平的知识理解建立在知觉水平的理解之上，是对事物的本质与内在联系的揭示，主要表现为能够理解概念、原理和法则的内涵，知道它是“怎么样”的;高级水平的知识理解属于间接理解，建立在概念理解的基础之上，使知识得到广泛迁移，达到系统化地步，有利于认知结构的重建，达到知识融会贯通的地步，知道它“为什么是”。

知识理解能力的培养和提高离不开旧知与新知的衔接，而旧知与新知的衔接需要以旧知的迁移为基础。因此，教师应在备课环节找准旧知向新知过渡的知识生长点，由旧知切入，基于知识生长点引导学生展开新知探究。鉴于小学数学的抽象性特征，教师可以凭借信息技术的支持，在引导学生探究旧知的过程中，将新知转化为直观、具象的内容。

在本课中，“圆的面积的含义”这个学习内容，建立在学生前面已学的圆的周长公式以及三角形、长方形、正方形、平行四边形等平面图形的面积的含义的基础之上。与新知联系最紧密的是三角形、长方形、正方形、平行四边形的面积的含义。课堂中，教师可以借助多媒体技术，为学生展示前面已学的四种图形，组织学生以小组合作学习的方式，探究四种平面图形的“面积的含义”的知识本质即各自“所占平面的大小”，驱动学生思维发展，使学生基于知识分析形成对平面图形的面积的规律性认知;依照演绎推理的规则，作为一种新的平面图形，“圆的面积的含义”自然也应是“所占平面的大小”;基于上面的推理，教师用动图方式呈现“圆的面积的含义”，帮助学生理解新知，提高知识学习的精准度，明确“圆所占平面的大小为圆的面积”这个新的知识点。

（二）借助信息的具象性，促进学生新知探究与知识分析能力的发展

知识分析能力是人在思维中把客观对象的整体分解为若干部分进行研究和认识的技能和本领。客观事物是由不同要素、不同层次、不同规定性组成的一个统一的整体，只有把它的每个要素、层次、规定性在思维中暂时分割开来进行考察和研究，搞清楚每个局部的性质、局部之间的相互关系以及局部与整体的联系，才能实现对客观事物的深刻认识。324E6EBE-7361-4F1F-9753-56761C0697B4

在小学数学教学中，应用信息技术的具象化优势，可以实现对新知的有效探究，降低学生学习新知的难度。

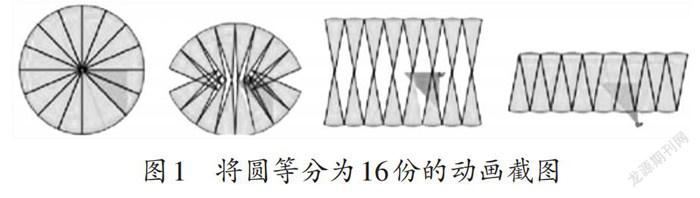
在“圆的面积”教学中，圆的面积计算公式及其推导过程是本课教学的重点和难点，对教学内容进行具象性设计不仅必要而且非常重要。课堂中，笔者首先应用多媒体动画，为学生展示了被等分成16份的圆的图形的展开过程。然后引导学生对展开图形的特征进行仔细观察，从中提取圆形中的关键要素半径和周长进行分析、研究，完成下面的知识探究任务：将被等分为16份的圆展开后进行如图1所示的拼接，你认为这个拼接的图形近似于哪个图形？学生很快便发现它“有点像长方形”。教师继续播放动图，依次将圆等分为20份、30份……学生可以发现：按偶数等分的份数越多，展开后拼接成的图形就越近似于长方形。

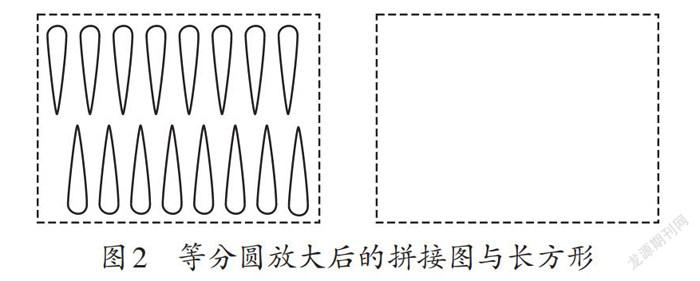
随着学生对“近似于长方形”的理解程度的加深，教师如图2所示将均分为16份的圆与一个长方形进行了并列展示，强化学生对圆转化为长方形的转化思想的感知。之后引导学生结合长方形的面积旧知，对圆形的关键要素展开对应的观察与思考，从而顺利推导出圆的面积的计算公式，过程如下：因为圆的半径近似于长方形的宽，圆的周长的一半近似于长方形的长，而长方形的面积=长×宽，所以，圆的面积=圆的周长的一半×圆的半径，即S=πr×r，S圆=πr×r=πr2。

（三）借助信息技术的情境性，促进学生新知应用与问题解决能力的发展

问题解决能力又叫解决问题能力，是指人们运用观念、规则、一定的程序方法等对客观问题进行分析并提出解决方案的能力。问题解决能力也有层次的分别：初级的问题解决能力表现在能够发现一般的显性问题，做出初步判断、简单处理;中级的问题解决能力表现在能够在自己熟悉的领域相对容易地发现隐藏的问题，有发现问题的基本技巧和一定的分析能力，能够根据现象探求解决问题的途径并找到答案，较好地解决问题;更高层次的问题解决能力意味着能够准确预测事情发展过程中的各种问题，并将其消灭在萌芽状态，同时归纳总结出问题发生的规律，指导他人提高发现和解决问题的能力。

问题解决能力的培养需要教师创设适合的问题情境，引导学生结合已学知识和生活经验展开问题分析，给出解决方案，进而解决问题。基于知识应用的问题解决能力，实为中级水平的问题解决能力。

在本课教学中，教师运用多媒体动画方式，创设了下面的问题情境：小刚量出一棵树某处的周长是157cm，请求出这棵树该处树干横截面的面积。鉴于问题中并没有直接给出圆的面积计算公式中的半径数据，笔者将学生分成了若干小组，让学生以小组讨论的方式探究情境中的问题解决方案。经过充分的讨论分析，学生给出了先求圆的半径、再求横截面面积的问题解决方案。随后笔者运用多媒体课件，向学生展示了如图3所示的问题求解过程。

（四）借助信息技术创设综合性问题情境，促进学生创新性思维能力的发展

创新性思维能力是学生在综合应用已学知识的过程中，对知识进行拓展思考，最终形成新思想、新理论、新方法、新发明的能力。教师借助信息技术，设置具有综合拓展性的学习内容，帮助学生在巩固已学知识和拓展学习相关知识的过程中，持续提高创新性思维能力，进而促进学生问题解决能力的进阶发展。

课堂中，笔者课件出示了下面的问题：CD的形状是圆形的，CD的中间为镂空圆，镂空圆的半径是2cm，整圆的半径为6cm，请问单面CD的面积是多少？鉴于不少小学生对CD这种事物缺乏基本的认知，笔者通过多媒体动画技术展示了一张CD的两面，同时将题目的条件和问题如图4所示展示给学生，给学生搭建问题解决的“脚手架”。

对照课件中的图示，学生给出了两种问题解决方案，并進行了解答。

解法一：已知R=6cm，r=2cm，则大圆面积S大=3.14×6×6=113.04（平方厘米），小圆面积S小=3.14×2×2=12.56（平方厘米），于是所求CD的单面面积SCD=113.04-12.56=100.48（平方厘米）。

解法二：题目所求CD单面面积SCD=3.14×（6×6-2×2）=100.48（平方厘米）。

师生共同整理解法一和解法二，可得环形面积计算公式：S环=πR2-πr2或S环=π（R2-r2）。

环状图形的面积计算公式来自圆的面积计算公式，是对圆的面积计算公式的拓展应用与实践创新。接下来的问题，将进一步拓宽学生的思路，引导学生综合之前所学知识，提高问题分析和解决能力。

教师运用多媒体为学生展示了一个圆内接正方形的动图，相关截图如图5所示，让学生思考以下问题：“当圆的直径为2cm时，怎样求出该圆与其内接正方形之间阴影部分的面积？”有了之前将整体拆分为部分的问题解决经验，学生很快便给出了该问题的解决方案：先求出圆的面积和正文形的面积，再用圆的面积减去正方形的面积，剩下的便是阴影部分的面积。

三、教师实施信息化教学促进学生高阶思维能力发展的建议

数学知识的多样性、综合性、系统性增加了学生学习的难度。教师要有效推进信息化教学，必须做好充分的准备。

首先，信息技术的发展日新月异，教师要不断学习，努力提高自身的信息技术驾驭能力，以利于灵活采用适合的信息技术手段，创设适合学生深度学习的教学情境。

其次，任何学科的课堂教学，都应以学科能力和核心素养的发展为重，因此设计信息化教学，重点在于建立一个有利于促进学生学科能力和核心素养形成和发展的结构合理的教学框架。

最后，为了达成学生高阶思维能力发展的目标，教师要基于教学框架建设课程内容，不断丰富教学资源，善用信息技术有效突破数学抽象的学习难点，为学生数学思想的建立和数学能力的发展奠定坚实的基础。

参考文献

[1]孙宏安.高阶思维能力及其培养[J].大连教育学院学报，2018，34（2）：14-19.

[2]萧浩辉.决策科学辞典[M].北京：人民出版社，1995.

[3]冯世华.从中层到中坚：职业化中层管理者成长的8项修炼[M].北京：中国财富出版社，2015：53.

[4]夏培培.以问题为“驱动”发展学生数学高阶思维能力：以“几何最值问题”的专题探究为例[J].中学数学（初中版）下半月，2019，580（6）：44-46.

作者简介：范燕（1977— ），广西柳州人，高级教师，主要研究方向为小学数学教学。

（责编 白聪敏）324E6EBE-7361-4F1F-9753-56761C0697B4