基于线声源模型的交流输电线路可听噪声三维预测方法

林旗力，朱克亮，童佳君，陈文杰，谢紫银

（1.中国电力工程顾问集团华东电力设计院有限公司，上海 200001；2.浙江大学 环境与资源学院，杭州 310058；3.国网安徽省电力有限公司建设分公司，合肥 230022）

0 引言

输电线路可听噪声是指输电线路电晕放电产生的人耳可以听到的噪声［1］，本文简称为“噪声”。在以特高压为代表的高电压等级架空线路设计咨询中，噪声已成为影响导线选型、杆塔设计等环节的重要因素之一［2］。噪声预测的准确性对优化线路设计方案、提高其环境友好性具有重要意义。

20世纪60年代以来，美国、日本、意大利等国家都曾研究提出特高压线路对称分裂导线噪声的预测公式［3］。美国IEEE电晕和电场效应工作组对各国预测方法进行了分析，指出BPA（美国邦维尔电力局）的推荐公式误差最小［4］。我国相关研究始于20 世纪90 年代，初期一般采用BPA 公式预测特高压交流线路噪声。唐剑、陈豫朝、万保全等［5-9］利用电晕笼试验装置，对交流线路声功率计算方法、噪声预测公式等展开了深入研究。谢辉春等［10］在武汉特高压交流试验基地通过对线路噪声的连续测试获得了实测数据。张业茂等［11-12］在特高压交流试验示范工程和1 000 kV 皖电东送特高压交流工程沿线建立了4座观测站，对线路噪声开展大量实测工作。李鹏飞等［13］利用特高压线路长期观测站监测的纯声及天气参数，分析降雨量、大气压等天气因素与纯声的相关性。张建功等［14］通过对750 kV/330 kV混压同塔输电线路的仿真计算，得到不同导线排列方式下、不同高度处，以及不同时间、空间条件下“100 Hz”纯声的分布规律。

目前，交流线路噪声计算中通常假定线路为无限长直导线，得到的结果为导线位于统一高度时沿导线径向的噪声二维分布。在实际环境中，线路是悬挂在相邻两基杆塔间的悬链线形状，导线最低点与挂点之间存在一定高度差（即弧垂）。针对该问题，谢龚浩等［15］采用模拟电荷法，搭建考虑导线弧垂影响的交流线路导线表面电场强度三维计算模型，并结合线路噪声声功率产生特性及点声源球面传播规律，建立有限长导线噪声三维分布预测模型。付万璋等［16］基于文献［9］提出的声功率级计算式，进一步搭建考虑多线路间相互耦合的噪声三维计算模型。但上述方法较为复杂，推广应用受到一定限制。因此，采用成熟的环境噪声预测软件对交流线路噪声三维预测方法开展研究，具有重要的现实意义。

为此，本文基于线声源模型，采用Cadna/A户外噪声预测软件，提出一种交流线路噪声三维预测方法，利用该方法对线路噪声进行实例研究，并分析相邻跨线路噪声和地面因子的影响，最后通过1 000 kV 皖电东送特高压交流工程实测数据验证该方法的准确性。研究结果可为我国高电压等级交流线路噪声预测工作提供一种科学且便捷的方法。

1 理论基础

1.1 导线几何模型

当架空线路的水平档距足够大时，金属导线的刚性影响可以忽略，且导线沿线长的荷载均匀分布，则线路悬挂形状可认为是悬链线。线路导线弧垂如图1所示，O点位于线路最低点，A和B为线路两端挂点。图1中：x为线路各点到纵坐标轴Y的水平距离；y为线路各点到横坐标轴X的垂直距离；yA和yB分别为挂点A 和B 到横坐标轴的垂直距离；β为高差角；σ为线路各点的应力；σ0为线路各点的水平应力（即最低点应力）；σV为线路各点的垂直应力；γ为线路比载，即单位长度单位截面上的荷载；l为档距，即两挂点间的水平距离；h为高差，即两挂点间的垂直距离；lOA和lOB分别为O点与挂点A和B间的水平距离；fx为线路弧垂（即两挂点连线上各点到线路上的垂直距离）；fm为线路最大弧垂（位于档距中心）；θA和θB分别为挂点A和B处线路与水平线的夹角。

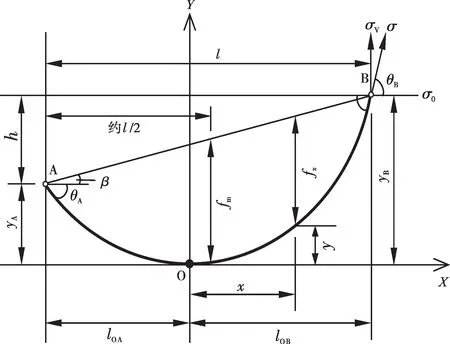
图1 线路导线弧垂

悬链线形状的线路弧垂fx的计算公式为［17］：

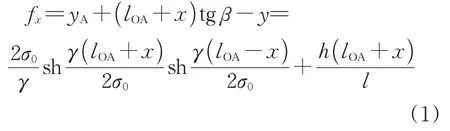
式（1）包含了双曲线方程，计算过程较复杂。为了简化计算过程，采用抛物线代替悬链线［17］，则线路弧垂fx计算公式为：

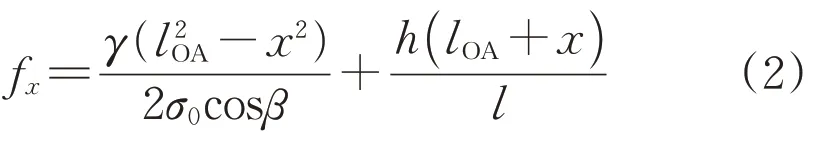
此时线路最大弧垂fm为：

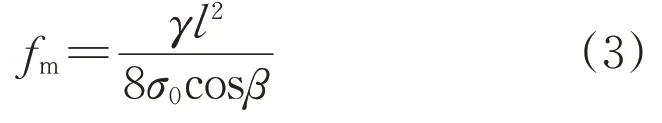
1.2 导线声学模型

声功率级的定义为声源声功率与基准声功率之比的常用对数，单位为dB。参照DL/T 2036—2019《高压交流架空输电线路可听噪声计算方法》，在大雨条件下，交流线路第i相导线单位长度A计权声功率级计算公式为［1］：

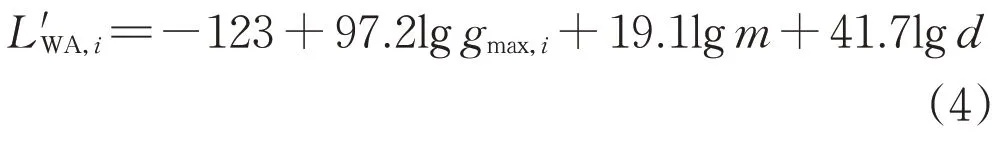
将线路导线看作有限长线声源。在有限长线声源计算中，Cadna/A 软件采用投影法：首先将线声源分为被遮挡及不被遮挡的两大部分，再将各部分微分成更小的区块，每个区块以等效点声源参与计算［19］。等效点声源位于区块的几何中心。

线声源微分区块长度的确定与该区块至预测点的距离有关。Cadna/A软件引入了微分系数Rj，其定义为［19］：

式中：lj为线声源第j个区块的长度；rj为线声源第j个区块中心至预测点的距离。

由式（5）可知，相同条件下Rj越小，线声源被微分的区块越多，计算量也越大。根据GB/T 17247.2—1998（ISO 9613—2：1996）《声学 户外声传播的衰减 第2 部分：一般计算方法》［20］，声源到预测点间的距离超过声源最大尺寸的2倍，是实际声源组可等效为该组中部点声源的必要条件之一。因此，Rj不宜大于0.5。

进一步地，计算得到第i相导线第j个区块等效点声源对预测点处的噪声贡献值LPA，i，j。

当等效点声源处于自由空间时：

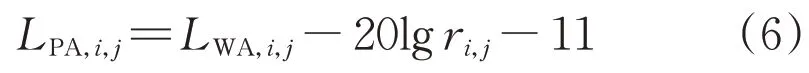
当等效点声源处于半自由空间时：

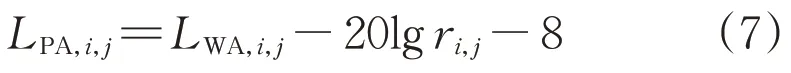
式中：LWA，i，j为第i相导线第j个区块等效点声源的A 计权声功率级；ri，j为第i相导线第j个区块等效点声源与预测点的距离。

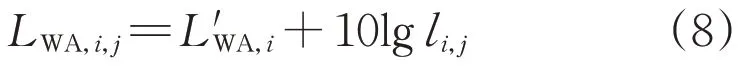
式中：li，j为第i相导线第j个区块的长度。

在此基础上，计算第i相导线对预测点处的贡献值LPA，i为：

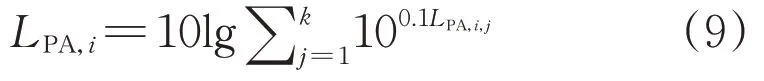
式中：k为第i相导线的区块总数。

假设线路共有n相导线，则线路噪声雨天L5值（即有5%的时间A声级超过的值）为：

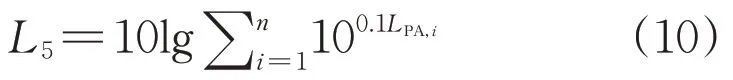
根据DL/T 2036—2019［1］，雨天L5值相当于大雨条件下线路噪声的值，而雨天L50值（即有50%的时间A声级超过的值）相当于雨天线路噪声的平均中值。雨天L50值也是GB 50665—2011《1 000 kV 架空输电线路设计规范》对线路噪声的建议控制指标［21］。

2 实例分析

2.1 分析对象及建模过程

2.1.1 分析对象

以1 000 kV 皖电东送特高压交流工程淮芜Ⅰ线、Ⅱ线514—515 号杆塔（同塔双回）作为实例［12］，采用本文预测方法对线路噪声进行计算分析。芜湖观测站段导线参数和布置情况见表1和图2。导线最低对地高度为34 m。两端杆塔设为等高，水平档距400 m。地面因子G表征地面对声波的吸收能力，取值范围为0～1［20］。根据现场实际条件，地面接近于疏松地面，所以模型中G取0.9。

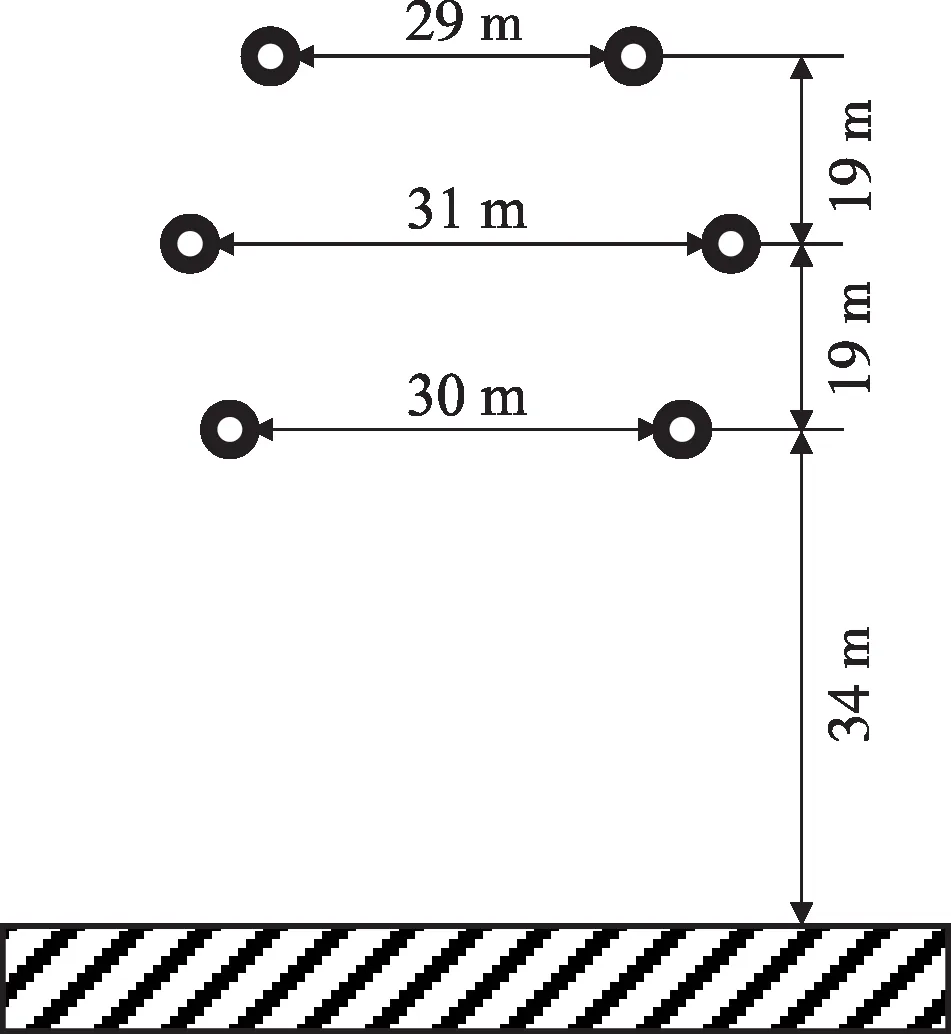
图2 分析实例导线布置

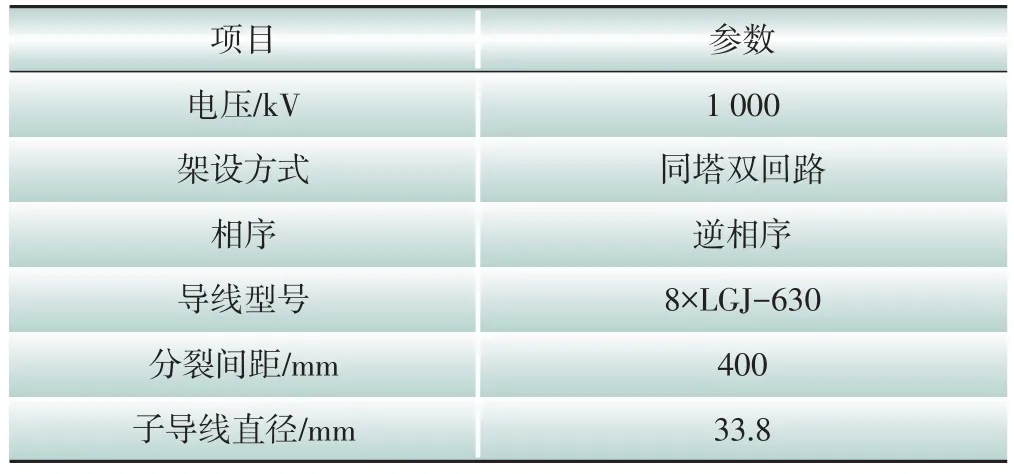
表1 分析实例导线参数

2.1.2 建模过程

本文提出的预测方法建模过程如下：

1）收集线路设计参数。

2）在制图软件（如AutoCAD）中建立线路三维几何模型。

3）将几何模型导入Cadna/A软件。

4）计算导线单位长度声功率级。

5）在Cadna/A软件中设置模型声学参数。

6）检查及调试模型。

7）运行计算。

在以往的研究中，通常是以单跨线路噪声作为分析对象。为了考虑相邻跨线路噪声的影响，本文建立三跨线路模型，如图3所示。线路依次为Ⅰ、Ⅱ、Ⅲ跨，分析对象为中间的Ⅱ跨线路。

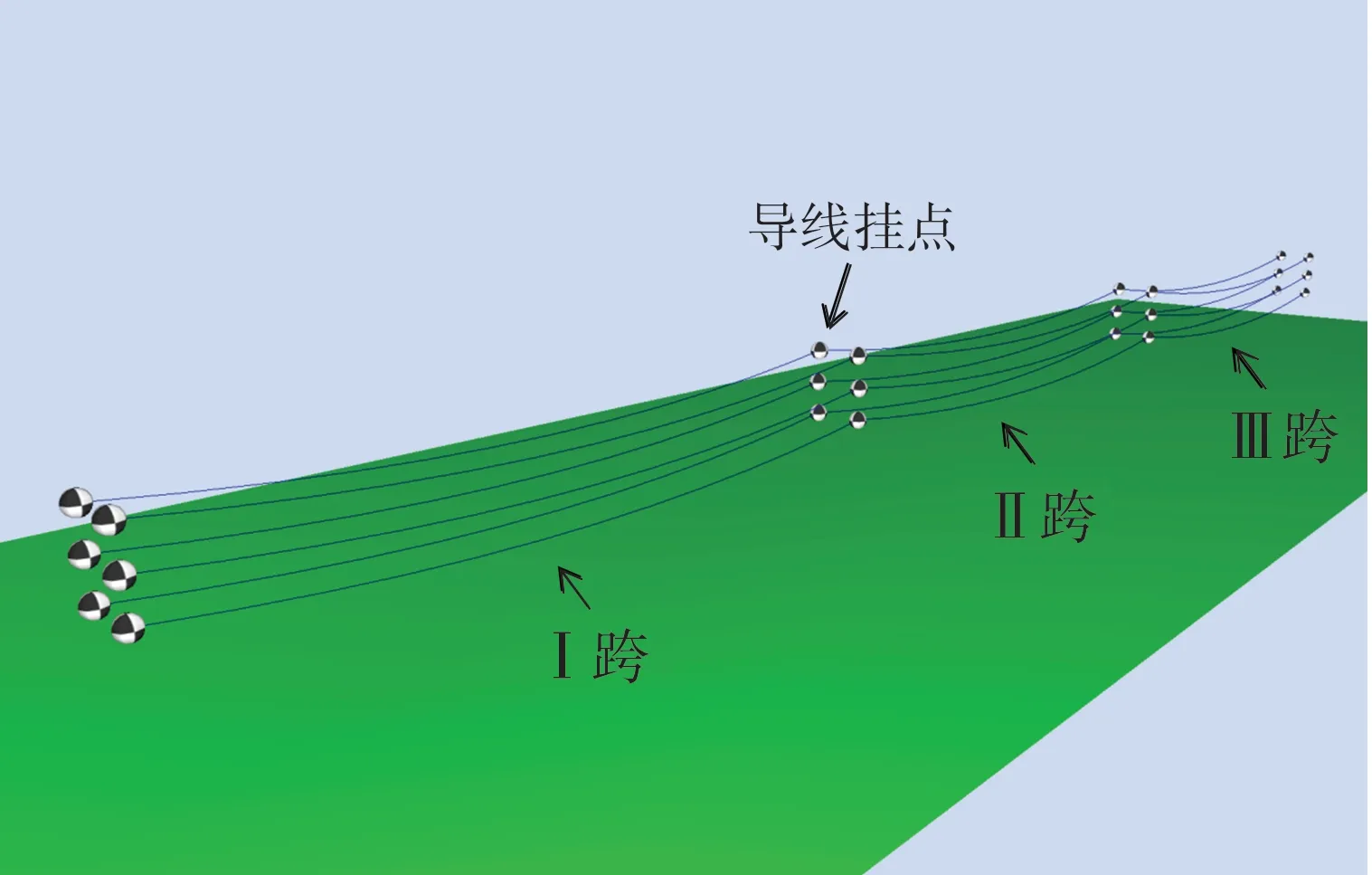
图3 三跨线路噪声三维模型

2.2 结果分析

2.2.1 线路地面噪声分布特性分析

以距地面1.5 m高度作为线路地面噪声分析高度［22］。根据预测结果，线路地面噪声雨天L5值如图4所示。由图4可看出，线路地面噪声关于线路中心线投影呈轴对称分布，且最大值出现在档距中心（即弧垂最大处）附近。

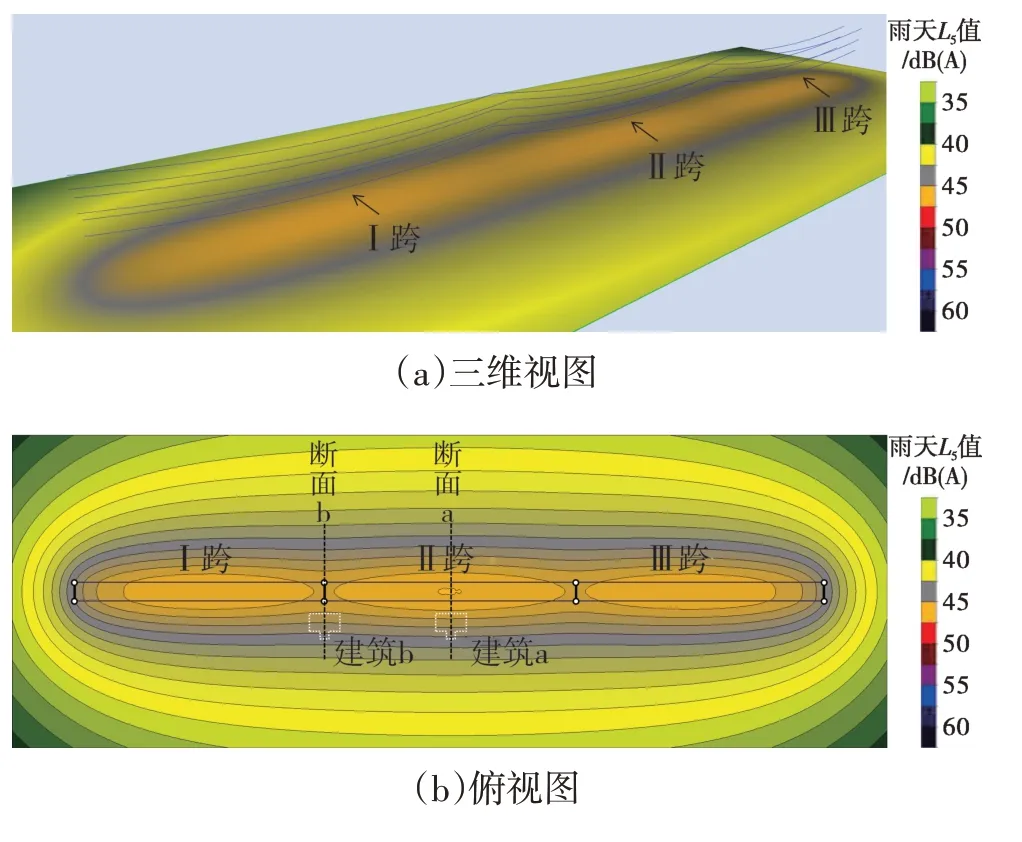
图4 线路地面噪声预测结果

图5给出了Ⅱ跨线路地面噪声轴向分布预测结果。由图5可知，由于线高的影响，在距线路相同水平距离上，档距中心线附近的地面噪声最大，并朝着档距端部方向逐渐减小。但随着水平距离的增加，线高的影响逐渐减小，例如在线路中心地面噪声雨天L5最大值和最小值之差为1.0 dB（A），而在边相导线外50 m处的差值仅为0.3 dB（A）。

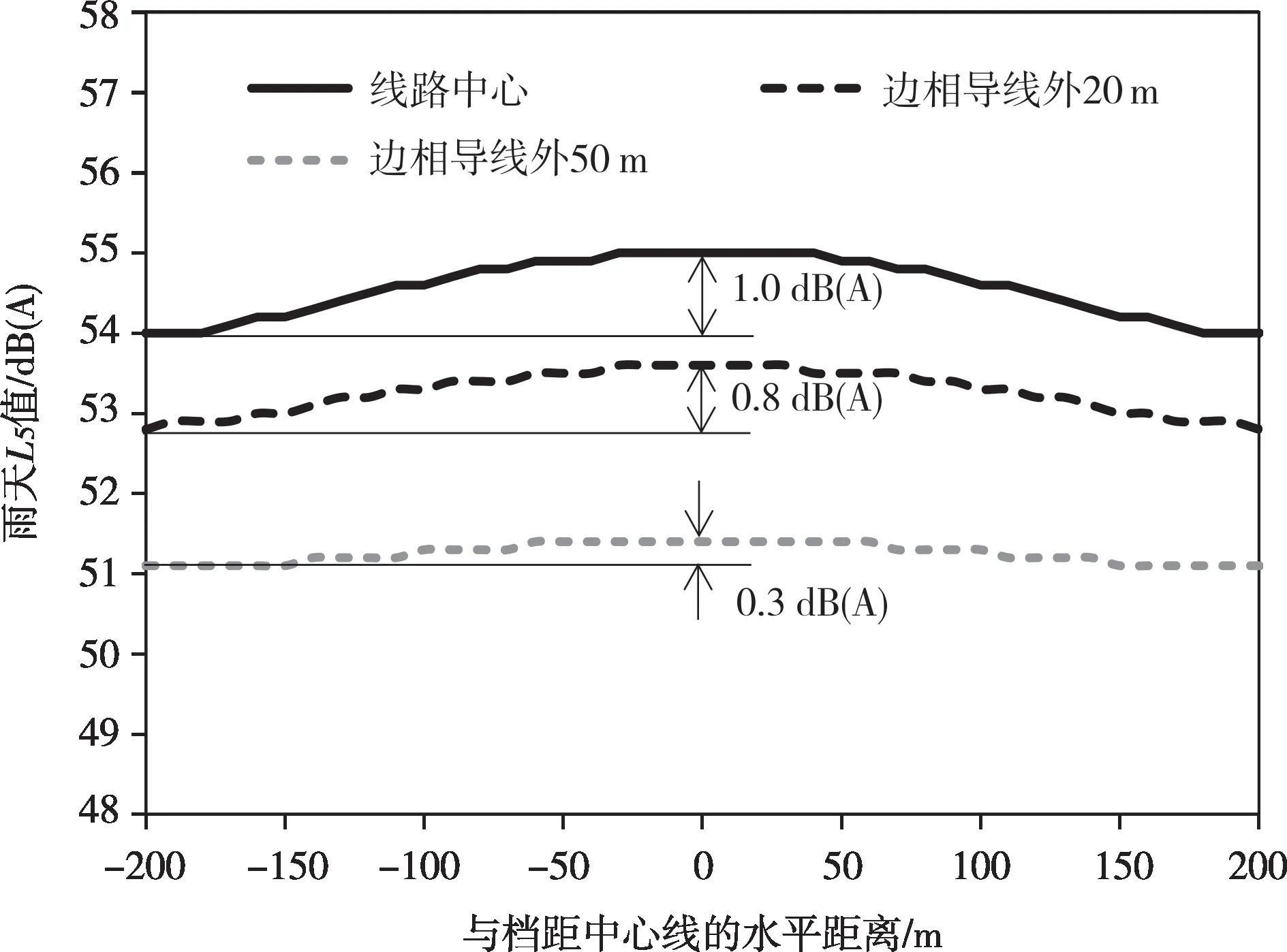
图5 线路地面噪声轴向分布预测结果

2.2.2 线路典型横断面及沿线建筑立面噪声分布特性分析

沿导线径向方向，分别在档距中心和档距端部设置横断面（位置见图4（b）），断面噪声分布预测结果如图6所示。由于断面a处的线高低于断面b，从图6 可明显看出，断面a 在线路下方的地面噪声大于断面b，但二者的差异随着与线路水平距离的增加逐渐减小。这与图5呈现的规律一致。

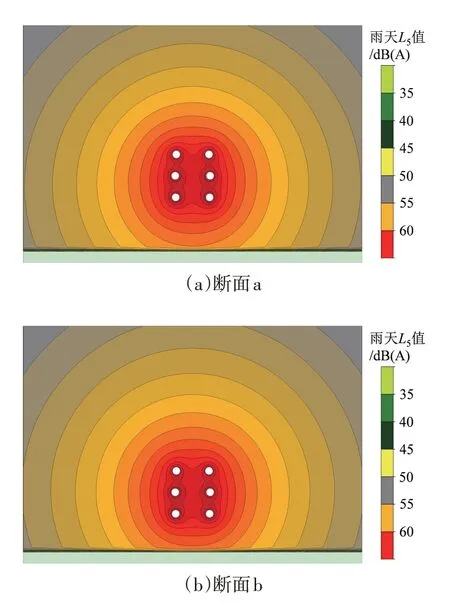
图6 线路典型断面噪声分布预测结果

从图6还可看出，线路沿线噪声随着高度的增加先逐渐增大，在与线路等高水平处到达最大值，之后逐渐减小。当前线路走廊资源日益紧张，线路沿线出现高层建筑的情况也越来越普遍。在断面a和断面b上各设置一座高100 m的建筑（位置见图4（b）），二者临线一侧立面与边相导线最近距离为20 m，得到两立面的噪声预测结果如图7所示。由图7可看出，随着高度的增加，2座建筑立面上的噪声先增大后减小。由于断面b处的线高高于断面a，所以噪声在建筑b立面上出现最大值的位置也高于建筑a。

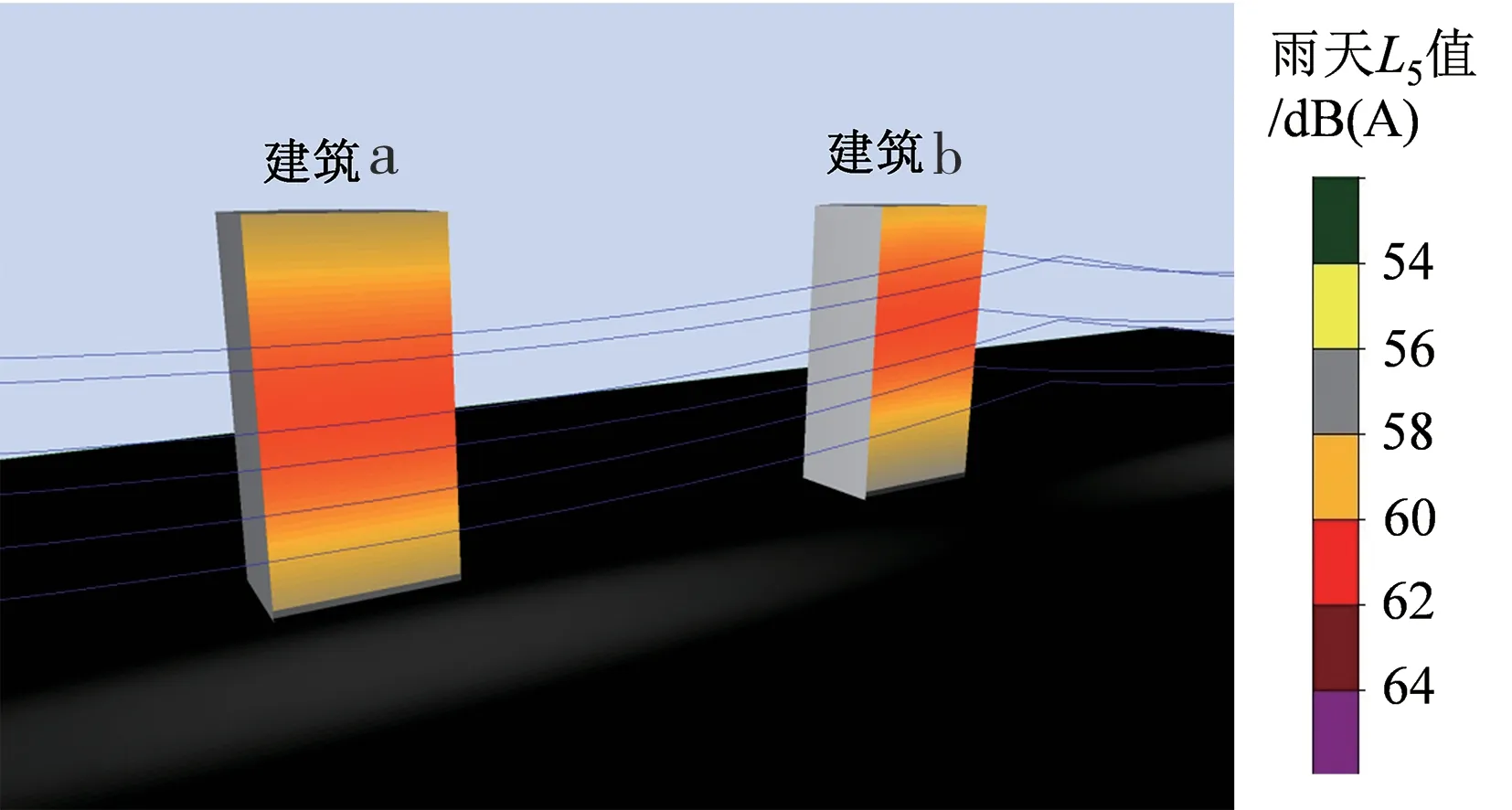
图7 沿线建筑立面噪声分布预测结果

2.2.3 相邻跨线路噪声影响分析

为了分析相邻跨线路噪声的影响程度，本文建立了单跨线路模型与三跨线路模型进行对比，即在三跨线路模型基础上删除Ⅰ跨和Ⅲ跨线路，保留Ⅱ跨线路。

根据预测结果，单跨线路模型得到的地面噪声L5值如图8所示。对比图4和图8可知，在Ⅱ跨线路沿线，三跨线路模型地面噪声高于单跨模型，其差值在档距中心处较小，在档距端部较大。以距边相导线20 m 处为例［21］，2 种模型线路沿线地面噪声轴向分布预测结果如图9所示。由图9可看出，三跨线路模型中线路沿线地面噪声雨天L5值高于单跨线路模型0.4～3.0 dB（A），该差值在档距中心处最小，并朝着档距端部方向逐渐增大。可见，线路噪声模型中考虑相邻跨线路噪声影响是必要的，尤其是当预测点靠近档距端部时。

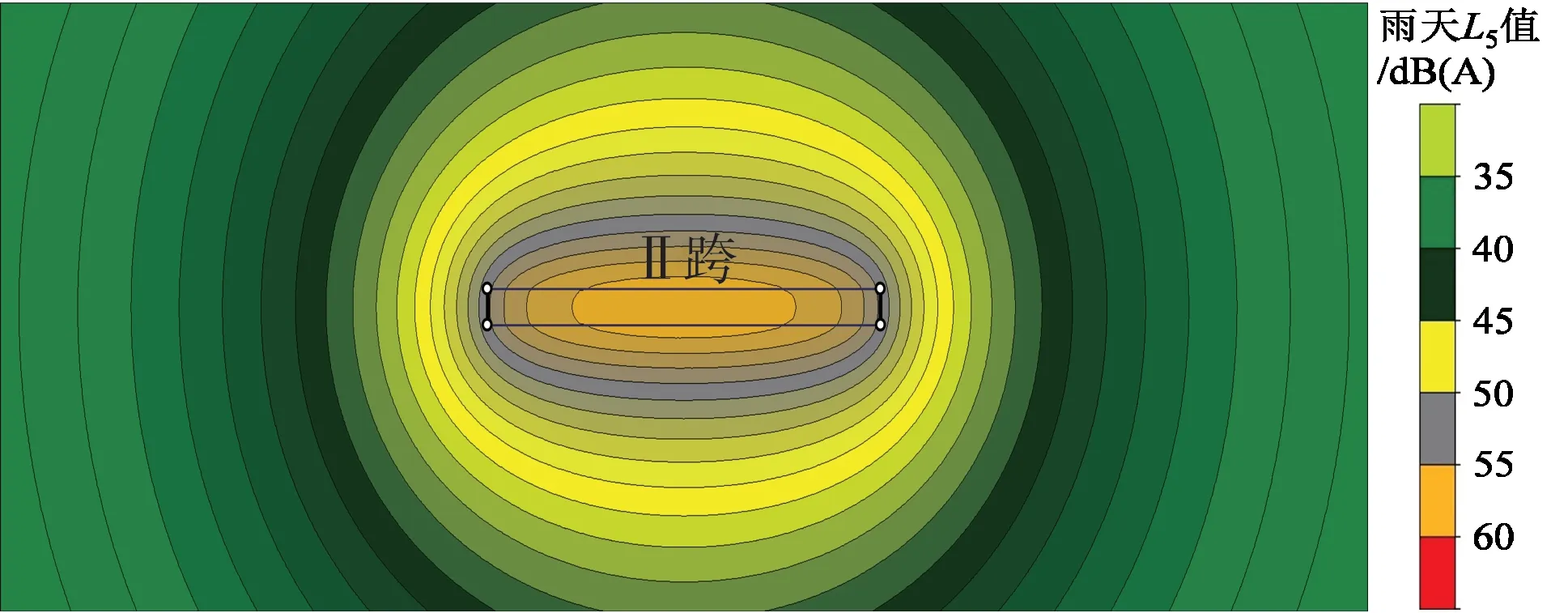
图8 单跨线路模型地面噪声预测结果

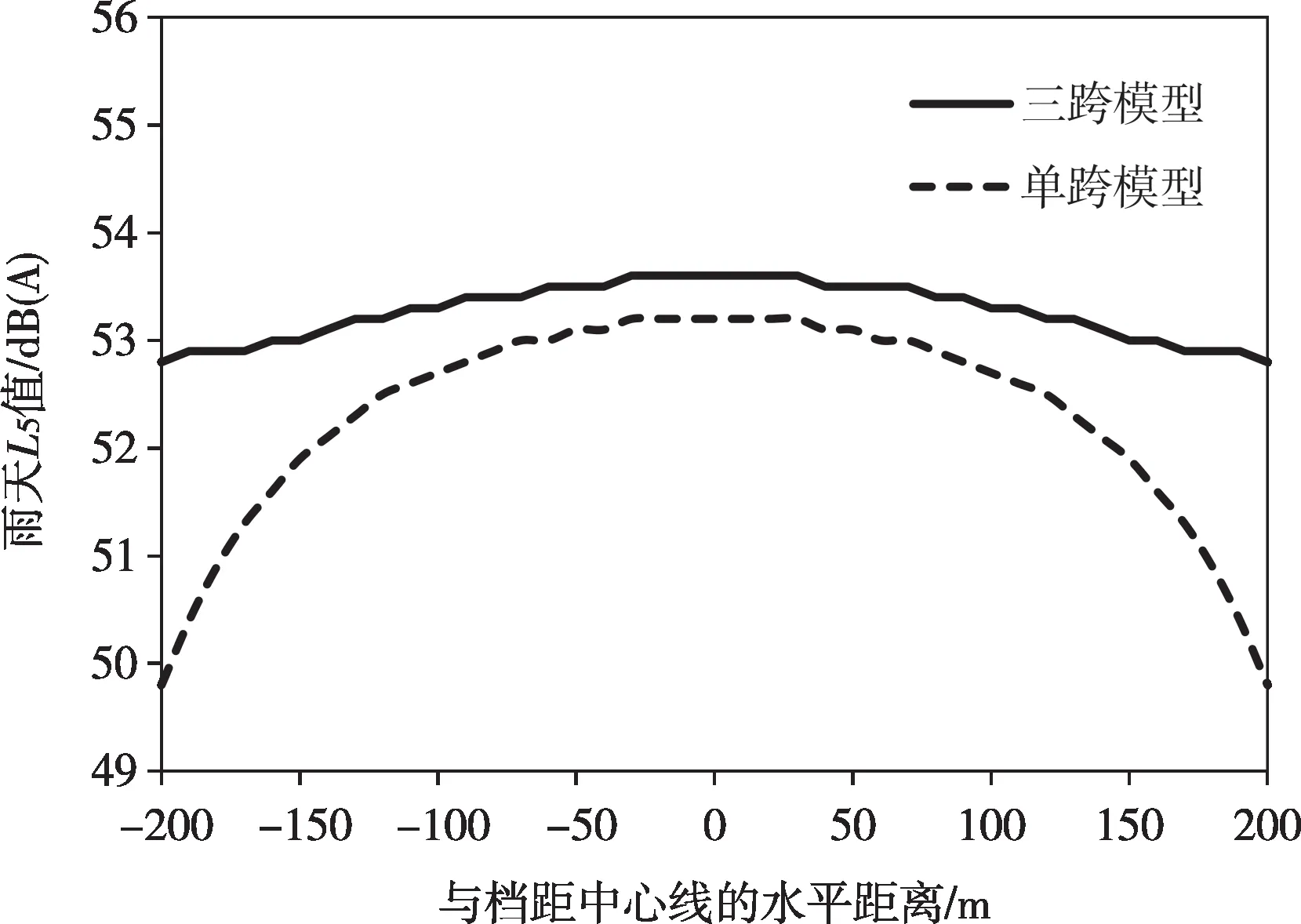
图9 2种模型线路沿线地面噪声轴向分布预测结果

2.2.4 地面因子G的影响分析

根据GB/T 17247.2—1998的定义［20］，坚实地面的G=0，疏松地面的G=1，混合地面的G为0～1 之间的值。G越大，表示地面对声波的吸收能力越强。

以往的研究较少关注G对线路噪声预测结果的影响。为此，本文在三跨线路模型中设置不同的G分别进行预测计算，得到Ⅱ跨线路距边相导线20 m处地面噪声轴向分布如图10所示。由图10可知，G与线路沿线地面噪声呈负相关，G=0 时（坚实地面）的雨天L5值比G=1 时（疏松地面）高6.4～6.6 dB（A）。

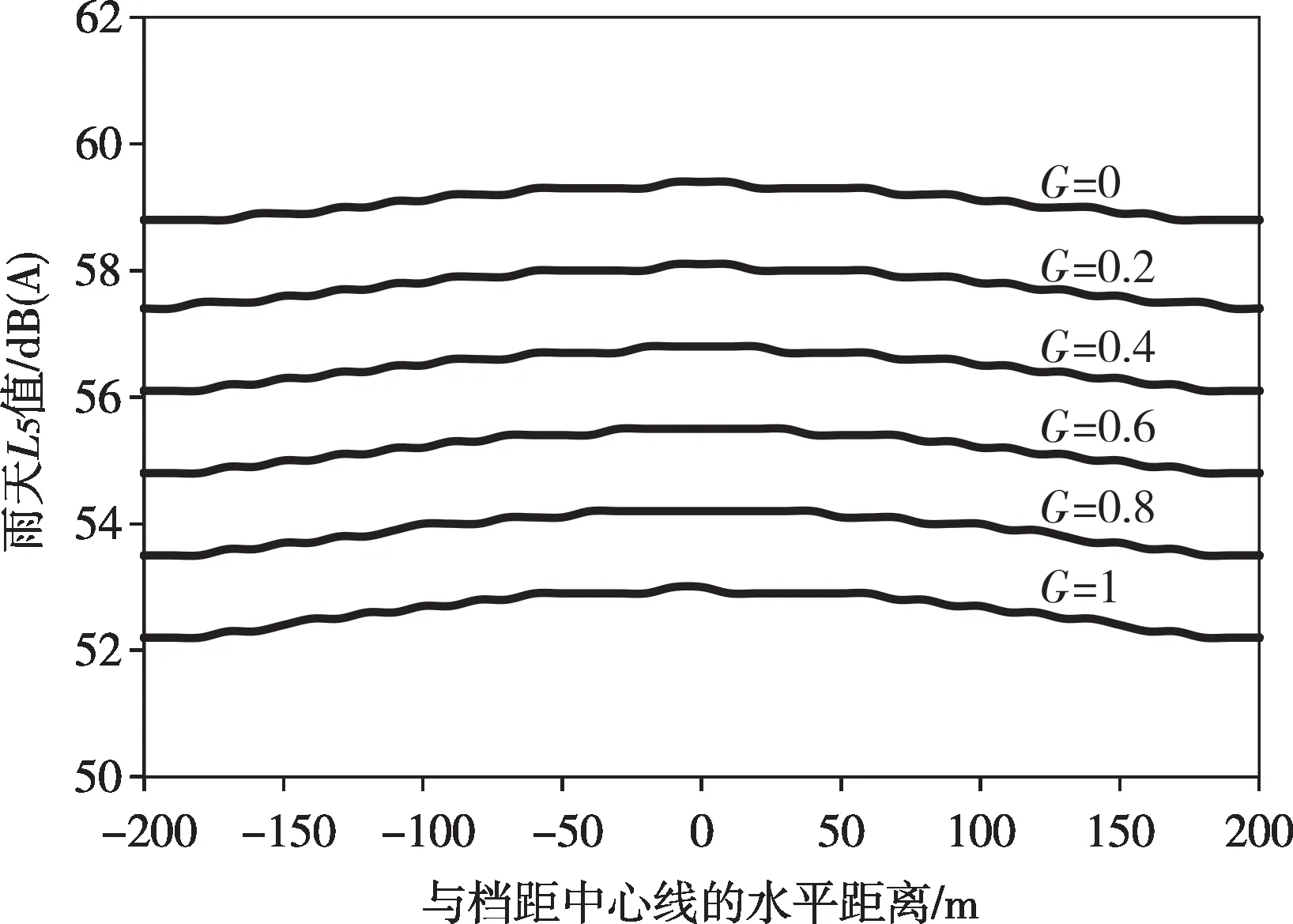
图10 G对线路沿线地面噪声预测结果的影响

以档距中心线上距边相导线20 m 的点位为例，图11 分析了G对不同高度噪声预测结果的影响。由图11 可看出，G对距地面3 m 以下的噪声预测结果影响尤为明显，而这个高度范围也是线路噪声预测关注的重点。因此，在线路噪声预测工作中，结合工程实际设置合理的G值是非常必要的。

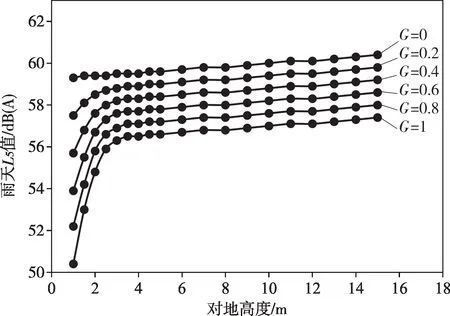
图11 G对不同高度噪声预测结果的影响

3 实测验证

张业茂等在淮芜Ⅰ线、Ⅱ线514—515 号杆塔档距中心线上建立长期观测站，对线路噪声开展了10 个月的长期观测，具体过程见文献［12］。表2 给出了线路噪声预测值与实测值，以及BPA 公式和BPA公式修正（减2 dB（A））后的计算结果［12］。由表2 可知，本文方法在线路边相导线外10 m 和20 m 处的预测值比实测值分别大0.9 dB（A）和0.4 dB（A），相对误差分别为1.8%和0.8%，与实测结果较相符。同时，本文方法预测值与BPA 公式预测值的修正结果较接近。

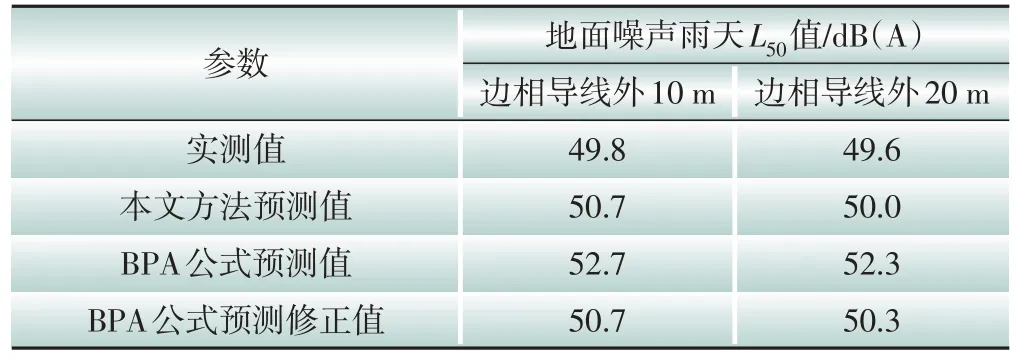
表2 线路噪声预测值与实测值比较

4 结语

1）本文从DL/T 2036—2019 推荐的导线声功率级公式出发，基于线声源模型，采用Cadna/A软件，提出一种交流输电线路噪声三维预测方法。

2）实例分析表明，由于线高的影响，在与线路相同水平距离上，档距中心线附近的地面噪声最大，并朝着线路两端方向逐渐减小。随着水平距离的增加，线高的影响逐渐减小。线路沿线噪声随高度的增加呈现先增大后减小的趋势，最大值出现在线路的等高水平处。

3）在线路噪声预测工作中，尤其是当预测点靠近档距端部时，考虑相邻跨线路噪声影响是必要的。地面因子G对线路噪声预测结果存在一定影响，尤其是对距地面3 m 以下的范围，预测工作中设置合理的G值是非常必要的。

4）采用1 000 kV 皖电东送特高压交流工程芜湖观测站的实测数据验证得到，本文方法在线路边相导线外10 m和20 m处的预测值仅比实测值分别大0.9 dB（A）和0.4 dB（A），相对误差分别为1.8%和0.8%，预测结果与实测结果较相符。