风电参与电网频率支撑的快速仿真模型

彭 琰，马骏超，金宇清，王晨旭，黄小俊，孙黎霞

（1.国网浙江省电力有限公司电力科学研究院，杭州 310014；2.河海大学 能源与电气学院，南京 211100）

0 引言

近年来，随着电力系统电源成分、网架结构和负荷特性的不断变化，电网频率稳定问题逐渐凸显［1-3］。华东电网曾在2015年发生过多次电网频率跌至49.9 Hz以下的事故［4-5］，这引起了电力工作者对于电网频率稳定和频率调节资源的广泛关注。新能源发电已经是电网中的重要电源，在2018 年颁布的行业标准《电力系统网源协调技术规范》中对新能源发电参与电网频率支撑提出了明确要求［6］。在各种新能源中，风电通常采用集中并网的形式且具有较好的调频能力，因此其参与电网频率支撑的作用得到了重视［7-8］。

目前，有关风电参与电网频率支撑的研究主要集中在单台风电机组的频率支撑控制策略方面［9-11］，部分研究涉及了风电场参与电网频率支撑时的内部机组协调问题［12-14］。MATLAB 仿真软件广泛用于开展控制策略研究，但是其应用于电力系统仿真分析还存在一些明显的不足：一是难以构建大规模电力系统的仿真模型，不利于评判控制策略对大电网的影响；二是控制器中的积分环节往往需要设置很小的仿真步长才能确保整个模型顺利运行，导致复杂模型或多元件模型的运行速度极慢，严重降低了研究效率。

为提高仿真模型的运行速度，对复杂模型进行简化是常用的方法。目前风电模型的简化主要用于电力系统的机电暂态仿真，具体方法是通过分群聚合的方式将风电场内众多的风电机组聚合为少数几台等效机组，从而大大简化风电场的机电暂态仿真模型［15-17］。但需要指出的是，在机电暂态仿真过程中，重点关注的是风电机组对电压跌落的响应及其故障穿越能力，因此对于风电机组的详细模型基本不作简化（或只简化电力电子变流器部分的模型），仅通过模型聚合的方法来降低风电场模型的复杂程度。风电参与电网频率支撑的研究主要关注风电对电网频率变化的响应，不涉及故障穿越，因此风电机组中电气部分的动态可完全忽略。此外，由于频率支撑响应过程较长，若要考虑风速变化的影响，则风电场内各机组的模型不能进行聚合。因此，目前广泛用于机电暂态仿真场景的风电场等效建模方法并不适用于风电参与电网频率支撑的研究，需要提出新的模型简化方法。

在用于电网频率问题研究的电力系统简化模型方面，仿真效率最高的简化模型是SFR（频率响应）模型［18］。经典的SFR模型仅适用于纯火电机组的电力系统，目前已拓展到可以适应含水电及新能源发电的电力系统［19］。然而，现有的SFR 模型是对完整电力系统的简化，用于分析整个电力系统的频率响应，风电场在现有SFR 模型中没有独立的模块，因此现有SFR 模型必须做适当的改进才能适用于风电参与电网频率支撑的研究。

针对以MATLAB 软件为工具开展风电频率支撑研究缺乏高效的仿真模型，且现有模型简化方法难以直接应用的问题，本文构建了一种基于风电机组简化模型和电网SFR 模型的快速仿真模型。首先，以DFIG（双馈感应风力发电机）为例，提出了一种仅保留机械动态过程的风电机组模型简化方法；然后，提出了一种排除风电频率支撑作用的电网SFR 模型获取方法；接着，通过风电机组简化模型和电网SFR 模型相整合以获得快速仿真模型；最后，算例验证了该快速仿真模型的有效性和高效性。

1 DFIG风电机组详细模型的简化方法

1.1 详细模型的简化方法

图1 是一种DFIG 风电机组详细模型的结构。DFIG风电机组的详细模型一般由风力机模型、轴系模型（图1中为两质块轴系模型）、双馈感应发电机模型、变流器模型、控制器模型等5 个部分组成。本文以MATLAB 软件提供的“DFIG Average Model”作为DFIG 风电机组的详细模型。该模型将电力电子变流器简化为等效电压源，其他部分保留不变。该模型中的控制器包括转速和桨距保留不变角控制器模型均为GE公司的风力发电机产品［20］。

图1 DFIG详细模型

由于本文并不涉及风电频率支撑控制方法的研究，因此仅采用了如式（1）所示的虚拟惯性控制方式。

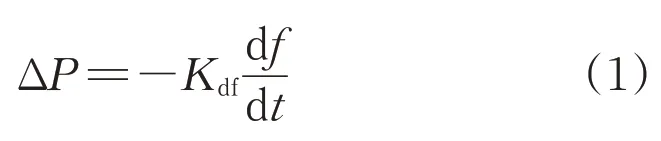
式中：ΔP为有功功率指令；Kdf为虚拟惯性控制系数；df/dt为频率变化率。

风电机组根据频率变化率df/dt产生一个附加的有功功率指令ΔP来改变机组的有功输出，从而实现对系统频率跌落的支撑。图2给出了虚拟惯性控制与DFIG详细模型中有功功率控制回路的整合方式。在本文后续仿真中，图2 中一阶惯性环节（起滤波作用）的时间常数Tf数值设定为1.0，虚拟惯性控制系数Kdf的数值设定为50。除整合虚拟惯性控制以外，本文未对“DFIG Average Model”作其他修改，便于研究人员重现本文构建的模型。

图2 虚拟惯性控制与风电机组详细模型有功功率控制回路的整合

电网频率的变化是同步发电机转速变化的反映，因此风电参与电网频率支撑的研究往往也采用机电暂态的仿真步长，而整个频率支撑过程历时（从风电机组释放转子动能提供有功功率支撑到最终恢复正常转速）超过100 s。为了提高DFIG风电机组模型的仿真速度并同时保持准确的频率响应特性，本文将DFIG风电机组的详细模型作了如下简化：

1）将两质块轴系模型简化为单质块轴系模型。

2）对于双馈感应发电机模型，只保留转子运动方程，忽略所有电气动态。

3）忽略转子侧和网侧变流器及其控制器的动态。

简化后的DFIG 风电机组模型结构如图3 所示，其由风力机模型、发电机模型（仅保留转子运动方程）、替代变流器及其控制器的有功功率计算系数KAP以及具备频率支撑控制的转速和桨距角控制器等4部分组成。

图3 DFIG的简化模型

由于简化模型中将两质块轴系模型简化为单质块模型，因此在发电机的转子运动方程中，感应发电机的惯性时间常数应与风力机的惯性时间常数相加。有功功率计算系数KAP替代了变流器及其控制器，其在简化模型中的作用是根据转速将电磁转矩指令Tecmd转换为有功功率Pe。根据DFIG简化模型的有功功率数值与DFIG详细模型的有功功率数值一致的要求，可以得到KAP的数值。KAP的数值是固定的，不随风速变化而变化。表1列出了DFIG风电机组简化模型中的部分关键参数，其中KAP是新增的参数，惯性时间常数H发生了变化，其他参数需要从详细模型的初始化程序中获得并设置到简化模型中。未在表1中列出的其他参数可直接采用详细模型中的数值。频率支撑控制策略和参数可根据研究需要单独修改，因此未在表1中列出。

表1 DFIG风电机组简化模型中的部分关键参数

1.2 简化模型的验证

为验证DFIG风电机组简化模型的有效性，搭建了如图4所示的IEEE 9节点系统。图4中G1和G2分别为水轮机和汽轮机；G3为是配备86台1.5 MW额定功率DFIG风电机组的风电场，用一个单机等效模型表示。同时将DFIG风电机组的简化模型和详细模型接入该系统进行仿真，风速设置为9 m/s。在仿真过程中，DFIG 风电机组的简化模型与详细模型共享风速和频率信号，但不输出有功功率。通过比较两种模型的有功功率响应曲线和转子转速变化曲线来验证简化模型的有效性。引起系统频率变化的扰动是Bus5上负荷功率突然增加15 MW，约为该系统总发电量的0.051 3 p.u.。

图4 IEEE 9节点系统示意图

图5为DFIG风电机组详细模型和简化模型的转子转速变化曲线。红色曲线表示DFIG风电机组详细模型的转子转速，蓝色曲线表示DFIG风电机组简化模型的转子转速。由于在对DFIG风电机组的详细模型进行简化时保留了所有与频率支撑控制相关的部分，所以DFIG风电机组简化模型与详细模型的转子转速变化曲线基本一致，最低转子转速差异仅为0.001 p.u。图6为DFIG风电机组详细模型和简化模型的有功功率响应曲线。红色曲线为DFIG风电机组详细模型的有功功率响应，蓝色曲线为DFIG 风电机组简化模型的有功功率响应。由图6可以看出，两种模型的有功功率响应曲线是吻合的。上述仿真结果证明了DFIG风电机组简化模型的有效性。

图5 详细模型和简化模型的转子转速变化曲线

图6 详细模型和简化模型的有功功率响应曲线

2 快速仿真模型的构建方法

2.1 排除风电作用的SFR模型获取方法

经典SFR 模型的结构如图7 所示，其中Δf为频率变化；ΔPd、ΔPm、ΔPa分别为扰动功率、机械功率和加速功率的变化量。经典SFR 模型中各参数的含义可以参阅文献［18］。考虑到本文建立快速仿真模型是为了研究风电的频率支撑控制，并不涉及经典SFR 模型中各参数的具体取值，因此，本文将经典SFR 模型简化为一个传递函数GSFR（s），如图7中虚线框所示。

图7 SFR模型的结构

同时，电网SFR模型中应当排除风电的响应。具体的方法是：首先，将完整电网仿真模型中的风电场用单机模型等效并屏蔽其中的频率支撑控制；然后，在电网内设置功率扰动，一般可设置为某个或某些负荷节点上功率的跳变；接着，记录电网频率的变化曲线；最后，以功率扰动为输入、以频率变化量为输出，辨识传递函数GSFR（s）。传递函数辨识可采用MATLAB 软件提供的系统辨识工具箱，本文不再赘述。

以图4 所示的IEEE 9 节点系统为例，连接Bus3 的风电场用单机等效模型表示，首先屏蔽其频率支撑控制；然后，继续采用1.2节所述的Bus5上的负荷功率扰动；根据其频率响应可以辨识得到如式（2）所示的三阶传递函数GSFR（s），其中s为拉普拉斯算子。在后续研究风电机组的频率支撑控制时，只要不改变电力系统中发电机的出力和调频参数，GSFR（s）就不需要改变，否则需要用上述方法重新辨识，即：

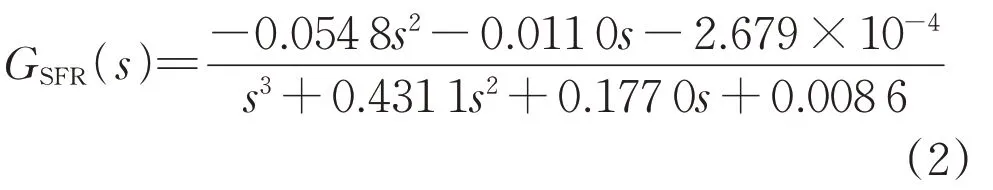
虽然本文中使用的IEEE 9 节点系统是一个很小规模的电力系统，但辨识GSFR（s）的方法同样适用于大规模的、实际的电力系统。通过使用实测的GSFR（s），可在MATLAB 软件下研究风电频率支撑控制策略在实际大电网中的控制效果。需要注意的是，当电网中同步机的开机组合发生变化时，电网的SFR 模型也会发生变化，应该使用本节所述方法重新辨识GSFR（s）。在风电参与电网频率支撑控制的有关研究中，重点关注的是风电本身的控制策略，通常不需要频繁改变电力系统的设置，因此不需要频繁地重新辨识GSFR（s）。

2.2 SFR与DFIG简化模型的整合方法

风电参与电网频率支撑研究的快速仿真模型是通过整合如图3所示的风电机组简化模型和图7所示的SFR模型来实现的。

图8（a）给出了SFR 模型和单台DFIG 风电机组简化模型的整合方法，图8（b）给出了SFR 模型与具有N台风电机组的风电场的整合方法，其中蓝色部分连接了SFR 模型和风电模型。SFR 模型输出Δf，Δf和稳态频率f0相加得到系统频率f。系统频率f被输入到DFIG 风电机组的简化模型中。在图8（a）中，单台风电机组输出的有功功率Pe减去其稳态值P0得到风电机组有功功率变化量ΔPDFIG，ΔPd和ΔPDFIG之差作为SFR模型GSFR（s）的输入量；在图8（b）中，不考虑风电场内部的集电网络及其损耗，N台风电机组的总输出功率（Pe1+Pe2+…+PeN）与风电场总功率的稳态值PΣ0相减，得到风电场有功功率的支撑量ΔPWF，ΔPd和ΔPWF之差作为SFR模型GSFR（s）的输入量。

通过上述整合方法所得模型即为本文所提出的快速仿真模型。需要指出的是，风电场内部各机组的风速在同一时刻各不相同［16］，而风电机组的频率支撑能力与风速密切相关，因此使用风电场单机等效模型得到的仿真结果是不准确的，应当使用保留全部机组的风电场模型，即如图8（b）所示的风电场快速仿真模型。

3 快速仿真模型的验证

3.1 模型有效性的验证

为验证本文构建的快速仿真模型的有效性和准确性，在相同的风速输入和负荷功率扰动下，比较如图4所示的系统详细模型与如图8所示的快速仿真模型的频率变化，结果如图9所示。红色曲线代表IEEE 9节点系统详细模型的频率响应，蓝色曲线代表快速仿真模型的频率响应。表2列出了两条频率变化曲线之间的差异。

图8 SFR模型与DFIG简化模型的整合方法

图9 详细模型和快速仿真模型的频率响应曲线

表2 详细模型和快速仿真模型的频率响应差异

从图9中可以看到，快速仿真模型的频率响应与IEEE 9节点系统详细模型的频率响应一致。表2中列出的3个频率变化指标误差很小，验证了快速仿真模型的有效性和准确性。

3.2 模型高效性的验证

表3 列出了图4 所示的IEEE 9 节点系统详细模型（风电场采用单机等效）和图8（a）、图8（b）所示的两种快速仿真模型的仿真速度数据。在进行仿真时，均采用定步长计算、“ode4（Runge-Kutta）”算法、“Accelerator”模式。由于较大的仿真步长会导致IEEE 9节点系统详细模型计算失败，因此仿真步长设为1 ms。在型号为AMD Ryzen5 5600X的CPU 上完成一轮300 s 的仿真需要112.37 s。使用快速仿真模型时，仿真步长可以扩大到10 ms，但使用20 ms及以上的仿真步长依然会遇到计算失败问题。对于步长为300 s的仿真，若风电场采用单机等效，则如图8（a）所示的快速仿真模型只耗时0.86 s，仿真速度提高了130 倍。若对本文例子中的风电场完整保留86台风电机组，IEEE 9节点系统详细模型的运行时间超过2 h，如此慢速的模型难以用于开展研究，而如图8（b）所示的快速仿真模型仅耗时8.22 s，仿真速度提高了近1 100倍。从对比结果中可以看到，相比完整的含风电电力系统详细模型，本文提出的快速仿真模型具有非常优异的仿真效率。

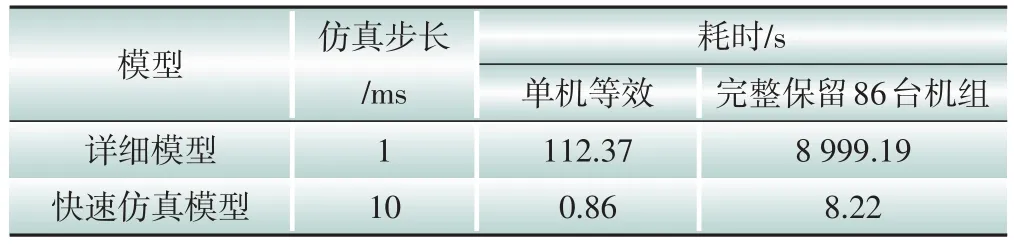
表3 系统详细模型和快速仿真模型的效率对比

3.3 工况变化在快速仿真模型中的体现

风电参与电网频率支撑所涉及的工况变化主要包括电网运行方式的改变和风速变化引起的风电场自身出力改变。

电网运行方式的改变在快速仿真模型中体现为电网SFR 模型参数的变化。本文2.1 节给出了SFR 模型的辨识方法，在电网运行方式调整后，通过系统仿真模型重新辨识SFR 参数即可，在本节中不再赘述。

对于由风速变化引起的风电场出力改变，如图8所示的快速仿真模型中完整保留了与风速输入相关的模块，因此可以适应风速的改变。风电场内各机组的风速可以使用实测的历史数据，或者使用文献［16］方法所建立的风速组合模型。利用文献［16］中给出的风速组合模型，可得到一个拥有48 台1.5 MW 风电机组的风电场在不同出力时各机组的风速数据。图10（a）给出了该风电场出力为40 MW 和60 MW 时的风速组合（从小到大排列），在使用快速仿真模型前需要设置各台机组风速。研究系统采用图4 所示的IEEE 9 节点系统，并采用1.2 节提及的功率扰动。图10（b）给出了风电场不同出力工况下的有功功率响应曲线，图10（c）给出了相应的电网频率变化曲线。由图10 可得，快速仿真模型完全可以应付工况的变化。

图10 风电场不同出力工况下的仿真结果

4 结语

MATLAB软件只能构建小规模的含风电电力系统模型，并且仿真速度缓慢。为了开展风电参与电网频率支撑控制研究，本文提出了一种由风电机组简化模型和系统频率响应模型整合所得的快速仿真模型。风电机组的简化模型中只包含与频率支撑控制相关的机械部分及其控制器，所有电气和电力电子部分均被简化。除风电以外的电力系统采用系统频率响应函数来表征，并可以在屏蔽风电机组频率支撑控制的基础上通过辨识方法得到。仿真结果表明：该快速仿真模型可显著提高在MATLAB 软件下进行风电参与电网频率支撑研究的效率，并可以模拟风电频率支撑对大规模电力系统的影响，对于促进风电参与电网频率支撑的研究有积极作用。