一种基于递归残差的回归模型变点检验
秦瑞兵,赵姣
(山西大学 数学科学学院,山西 太原 030006)
0 引言
变点问题最初由Page[1]提出,由于变点问题可以快速地监测到系统在任意时刻出现的变点并发出预警,避免决策上的失误,对减小损失,降低风险具有重要意义,因此从最初的产品质量控制领域逐步扩展到金融、气候、流行病学、信号过程和智能导航等领域。Küchenhoff等[2]用带有变点的趋势回归模型对时间序列进行分析,进而估计德国新冠病毒某一天发病的病例数。Basalamah等[3]研究了线性回归模型下的正态分布误差在检测回归参数变化时的情形,提出一种基于修正信息准则的检测方法来定位变点,该程序应用于美国国家航空航天局的数据来说明探测过程。
陈希孺[4]与Perron等[5]介绍了有关变点理论的研究与发展。Li等[6]针对分段平稳向量自回归过程,提出了一种三步法检测多重结构突变,用于多元时间序列变点估计。Shi等[7]用基于秩的回归方法对于多变点连续分段线性回归模型去同时估计回归系数和阈值的位置,实现了鲁棒性。Lu等[8]将模糊变点算法与M估计相结合实现了回归模型中的变点和回归参数的鲁棒估计。Brown等[9]提出了在变点理论广为应用的CUSUM统计量和CUSQ统计量。Sen[10]导出基于递归残差的CUSUMrec统计量的极限分布为一个加权维纳过程的最大值,即使回归模型的自变量包含因变量滞后项滞后,该统计量的极限分布仍然正确,Ploberger和Krämer[11]考虑用最小二乘回归残差代替递归残差构造了CUSUMols统计量,此统计量除了在变点发生时刻靠前的情形功效并不高之外,相较于CUSUMrec统计量,对于变点发生时刻靠后的情形功效有较大提高。对此Brown[9]基于递归回归残差平方序列,构造 CUSQrec统计量,Ploberger和 Krämer[12]导出了 CUSQrec统计量的极限分布。Deng与Perron[13]在一般混合条件下得到了CUSQrec统计量和CUSQols统计量的极限分布,对文献[12]CUSQ统计量的极限分布做了系数修正,得到CUSQ统计量的极限分布为一个布朗桥过程的最大值。Ploberger和Krämer[14]考虑了CUSUM统计量和CUSQ统计量的局部势函数,得出CUSQ统计量有很小的渐近局部势而CUSUM统计量有较大的渐近局部势,除非变点的系数偏移量正交于解释变量的均值向量,但由于局部性质对于发生较大偏移的情形并不适用,Deng与Perron[5]考虑了CUSUM统计量和CUSQ统计量的非局部势函数的性质,表明CUSQ统计量在非局部的情形下有较高的功效。基于以上方法,Nielsen和Sohkanen[15]将CUSQ检验统计量推广到具有确定性时间趋势的非平稳自回归分布滞后模型,将渐近理论更广泛地应用于最小二乘残差的检验。
但是当变点发生时刻靠前时,递归残差的CUSQ检验功效较低。本文将递归残差序列分为两组,比较两组递归残差平方的算术平均值,构建检验统计量,推导其渐近分布,并得到其在备择假设下的渐近极限。模拟结果表明本文构造的检验统计量比已有统计量在变点发生时刻靠前的情形功效有较大提高。
1 模型与假设

2 主要结论



3 数值模拟
本节通过数值模拟来分析本文所给方法的有限样本性质,并与文献[5]中的方法进行比较。首先生成120个独立同分布的标准正态随机数,代入统计量(5)中,重复该试验5 000次,可以计算得到显著水平α=0.05的临界值为8.470 2。为方便与文献[5]比较,考虑用模型(1)生成数据:xt={x1t,x2t}={1,(-1)t}′,备择假设中系数 βt的变化由 δ=b[cos(φ),sin(φ)]′来确定,其中 φ 是 δ和 xt的均值向量的夹角,分别取值为 φ=0◦,45◦,90◦,λ取 0.3,0.5,0.7,ut为标准正态随机数列。表1上部分为文献[5]中的实验结果,下部分为本文中方法重复试验5 000次中统计量拒绝原假设频率保留两位小数的结果。对比表1上下两部分,可以看到:(1)本文构建的统计量在原假设成立时,其经验水平更接近检验的显著水平0.05;(2)当变点发生在序列早期时,本文的统计量比传统的基于递归回归残差的CUSQ统计量具有较高的功效。当变点发生在序列后期时,本文方法的功效也均高于或等于已有基于递归回归残差的CUSQ统计量。这与定理2的结论相吻合。
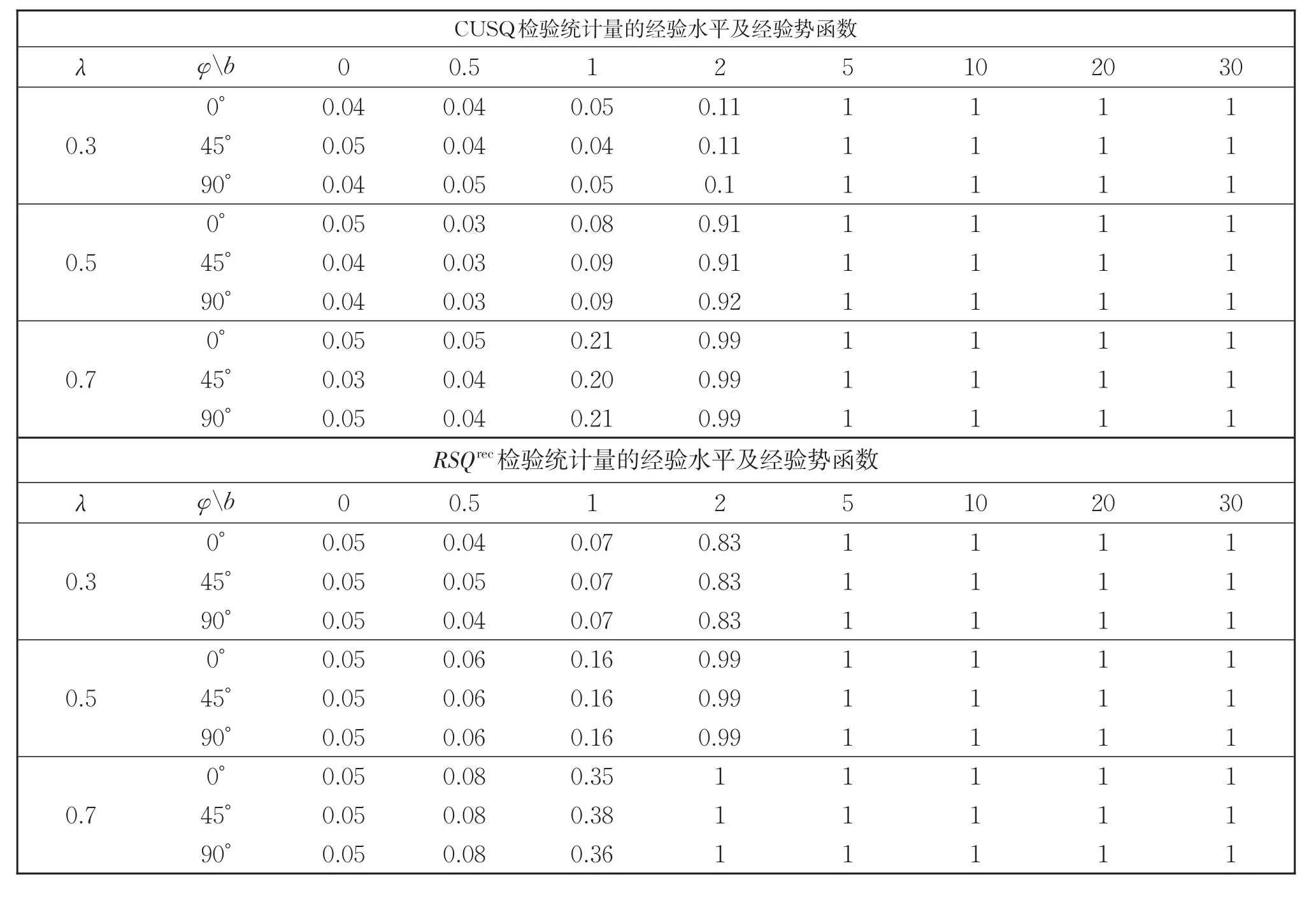
表1 检验统计量的功效Table 1 Power of the test statistics
4 结论
本文所构造的统计量对犯第一类错误的概率与选定的显著水平0.05更接近,同时,在检验有限样本下有更高的功效。在变点发生时刻靠后的情形下,功效也逐渐趋于1,对于变点发生时刻靠前的情形,较已有统计量有更高的功效。
但本文仅考虑误差为正态分布的情形,未考虑误差为非正态分布的情形以及误差具有相依性的情形。如何基于递归残差和最小二乘回归残差构造适合于误差是非正态分布和误差之间具有相依性情形下线性回归模型系数变点检验问题上,有待进一步研究。

