一种可外包解密的高效密文策略的属性基加密方案

李婷，常利伟

（1.山西财经大学 网络与信息教育技术中心，山西 太原 030006；2.山西财经大学 信息学院，山西 太原 030006）

0 引言

公钥加密是保护存储和传输信息机密性的一种强大机制。传统意义上，加密被视为一个用户定向传输给指定用户或者设备数据的一种方式。虽然这对“让数据提供者明确知道他想要将该数据共享给谁的应用”是非常有用的，但是在很多应用中，是提供者想要根据一些属性特征将数据信息发送给特定用户，以共享私密数据信息。

云计算是一种非常迷人的计算范式，计算和存储都从终端设备转移到云上。这种新的流行范式为企业和个人管理在分发和共享内容的方式上带来了重要的变革和大胆的创新［1］。通过将自己的信息技术能力外包给一些云服务的提供商，云用户可以大幅降低成本。如何保障云计算用户的数据安全是公众普遍关注的问题。部分外包数据是敏感的，只能由经过授权的数据消费者在远程位置访问。

加密技术是实现这一目标的基本方式。例如：属性基加密（ABE）是一种功能强大的加密访问方式。属性基加密的概念最初是由Sahai和Waters提出的［2］。而根据其访问控制策略部署方式可区分为两种不同的加密系统，即密钥策略的属性基加密（KP-ABE）和密文策略的属性基加密（CP-ABE）［3-7］。在 KP-ABE 方案中，密钥与访问控制结构相关联，密文与属性相关联（使用属性集合对明文进行加密，属性相当于公钥），且其访问控制结构由私钥产生中心（Private Key Generator，PKG）来控制分发，谁能解密不由加密人控制，而仅由PKG控制，PKG为每个属性分发相应的密钥，而只有当解密属性集合满足访问结构时才可解密；在CP-ABE方案中，密文与访问控制结构相关联，密钥与属性相关联（使用属性集合对密文进行解密），其访问结构由加密者控制，由加密者决定谁可以对密文进行解密，因而灵活性更强，只要是满足加密者所规定的访问控制结构的属性集合的解密人均可对密文进行解密，从而实现了一对多的访问控制。此后在具体的非交互假设下，Waters等［8］提出了一种新的方案来实现抗合谋攻击的密文策略的属性基加密系统。这之后Lewko等［9］又提出了一个完全安全的属性基加密方案，进一步充实了属性基加密的安全可用性。但属性基加密的加解密过程都存在很多双线性映射对的计算，很大程度限制了计算效率，而外包解密可极大提高属性基加密的使用效率，如文献［10-11］的方案。

外包解密的常用方法是对用户的私钥进行盲化后再传送给云服务器，然后云服务器利用盲化后的私钥即转换密钥来对密文进行部分解密从而得到相应的转换密文，用户最后只需要对已经部分解密过的转换密文进行解密计算即可，即进行少量的计算便可得到密文相对应的明文。用户在本地只需要进行简单的解密运算即可得到明文消息，即以少量的计算资源为代价来换取消息的保密性，如文献［12-15］的方案。近些年还出现了很多可追责、可验证及支持属性撤销的外包解密的属性加密方案，如文献［16-17］的方案。

本文给出了一个高效的、抗合谋攻击可证明安全的可外包解密的密文策略的属性基加密方案，其组织结构为：第一部分，介绍了方案中所需的基础知识；第二部分，给出高效外包解密方案的构造及正确性分析；第三部分，对高效外包解密方案进行了安全性证明；最后全文总结。

1 基础知识

1.1 双线性映射

假设存在两个阶为素数p的乘法循环群G，GT及一个双线性映射函数e：G×G→GT，且此双线性映射e属性如下：

（1）双线性：对于所有的u，v∈G及a，b∈Zp，存在e(ua，vb)=e(u，v)ab；

（2）非退化性：e(g，g)≠1。

如果G上的群运算及双线性映射e：G×G→GT是可高效运算的，则称G为一个双线性映射群。因为e(ga，gb)=e(g，g)ab=e(gb，ga)，故而双线性映射e具有对称性。

1.2 判定性平行双线性Diffie-Hellman幂元假设

选择一个与安全参数相对应的阶为素数p的群G，随机选择a，s，b1，…，bq∈Zp及生成元为g的群G。

如果一个敌手给出：

1.3 访问结构

1.4 线性密钥共享方案（LSSS）

假设存在一个l×n的矩阵M，称作分享生成矩阵，函数ρ表示矩阵M第i行的参与者，矩阵M第i行映射到ρ(i)属性上。

设垂直向量 v=(s，r2，…，rn)，其中 s∈Zp是将要分享的密钥，r2，…，rn∈Zp是随机数，那么向量Mv表示对密钥s分配给l个参与者的秘密份额。

LSSS方案具有线性重构的特性。设S∈T是一个访问授权集合，参与者下标集合I={i：ρ(i)∈S}⊂{1，2，…}，那么可以在多项式时间内找到一组常数{ωi∈Zp}i∈I，如果{λi}是对秘密 s的有效分享份额，则等式 ∑ωiλi=s(i∈I)成立。

2 高效外包加密方案的构造

参数生成（U）：参数生成算法，输入系统中的属性值。选择一个阶为素数p的群G，选择生成元 g和 U，随机群元素 h1，…，hU∈G，是与系统中属性U相关联的。另外，选择随机幂元α，a ∈Zp。

公钥为：PK=g，e(g，g)α，ga，h1，…，hU。

授权集合作为主密钥：MSK=gα。

加密算法（PK，(M，ρ)，M）：加密算法，输入公共参数PK和明文M，另外输入密钥共享访问结构(M，ρ)。函数ρ将矩阵M的行与属性关联起来。

M是l×n的一个矩阵。该算法首先选择一个随机矢量 v=(s，y2，…，yn)∈ Zp。该值将被用来共享加密幂次s。对从i=1到l，计算λi=υ·Mi，这里Mi是与M的第i行相对应的矢量。另外，该算法选择随机数r1，…，rl∈Zp。

解密算法(CT，TK，SK)：解密算法，输入相对于访问结构(M，ρ)的密文CT和集合S的私钥SK及相对应的转换密钥TK。假设S满足这个访问结构，则令 I⊂{1，2，…，l}定义为 I={i：ρ(i)∈ S}。同时假设{ωi∈ Zp}i∈I是这样一个常数集合，如果{λi}是任意与M相关的秘密s的有效共享，且满足 ∑i∈Iωiλi=s。（注意，存在其他的方法来选择ωi值来满足该要求）。

（1）外包解密

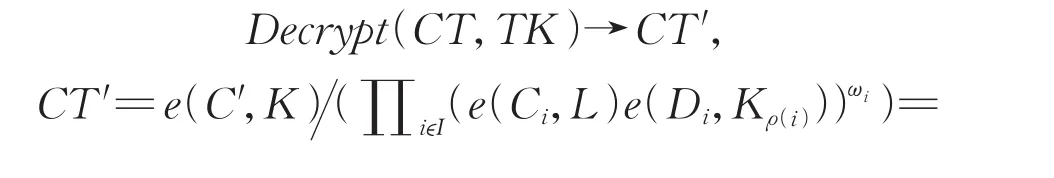
3 安全性证明

3.1 CP-ABE的安全模型

参数生成 挑战者运行参数生成算法，生成公共参数，并将公钥PK发送给敌手。

阶段1 敌手不断重复生成与属性集合S1，…，Sq1

相对应的私钥。挑战阶段 敌手发出两个等长的明文消息M0和M1。此外敌手给出一个挑战访问结构A*使得来自阶段1的集合S1，…，Sq1都不满足该访问结构。挑战者投掷一枚硬币b，在访问机构A*加密明文Mb。并将密文CT*发送给敌手。

阶段2 阶段1在限制条件下重复，属性集Sq1+1，…，Sq不满足与挑战对应的访问结构。

猜测阶段 敌手输出猜测结果b′或者b。

3.2 安全性证明

在证明我们系统安全中的一个重要步骤是简化“程序”的挑战密文为公共参数。

定理1 假定决策性q-parallelBDHE假设成立。不存在敌手可以在多项式时间内成功攻破该方案，其挑战矩阵为 l*× n*，且 l*，n*＜ q。

假定存在一个敌手A有不可忽略的优势∈=AdvA在选择安全游戏中攻破该方案。此外，假定该敌手A选择了一个维数小于q的矩阵M*。下面我们来演示模拟一个随机预言机B来模拟决策性q-parallelBDHE问题。

初始化 随机预言机从q-parallelBDHE挑战中取得参数y，T。敌手发送挑战访问结构(M*，ρ*)，其中 M*有 n*行。

参数生成 随机预言机选择随机数α′∈Zp，并 且 令 α=α′+aq+1， 则 有 e(g，g)α=e(ga，gaq)e(g，g)α′。 我 们 描 述 随 机 预 言 机 生 成群元素h1，…，hU。对每一个满足1≤x≤U的x选择随机值zx，再设X为指标i的集合，且有ρ*(i)=x。随机预言机程序hx值为；

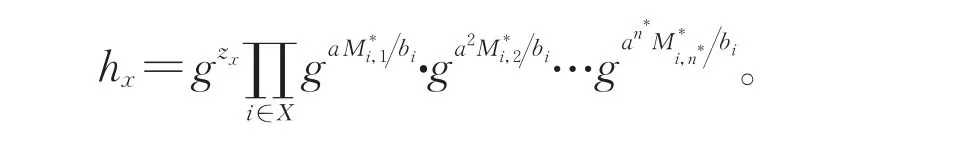
注意到，如果X=∅则有hx=gzx；且由于的取值，故而这些参数是随机分布的。

阶段3 在这一阶段随机预言机回答私钥询问。假定随机预言机收到一个集合S中的私钥询问，该集合S是不满足矩阵M*的。则随机预言机首先选择随机数z，r∈Zp，然后找到一个向量 ω =(ω1，…，ωn*)∈，其中 ω1=-1且对所有的 ρ*(i)∈S 中的 i都有 ω·M*i=0。通过前文中LSSS的定义可知一定存在这样的向量。注意，如果这样的向量不存在，则向量（1，0，0，…，0）在S张成的空间中。见阶段2中的讨论。

随机预言机隐式定义了t值，

现在必须计算出Kx(∀x∈S)。首先，考虑到当x∈S，则不存在i令ρ*(i)=x成立，则我们简单的令Kx=Lyx。

更加困难任务是为属性x∈S构建对应私钥组件的Kx，其中x在访问控制结构中使用。对于这些私钥组件，必须确保无法被模拟。但由于ω·Mi*=0，因此，所有的项都可以被消除。

同样，设X是所有i的集合，且ρ*(i)=x。在此基础上，随机预言机创建Kx如下：

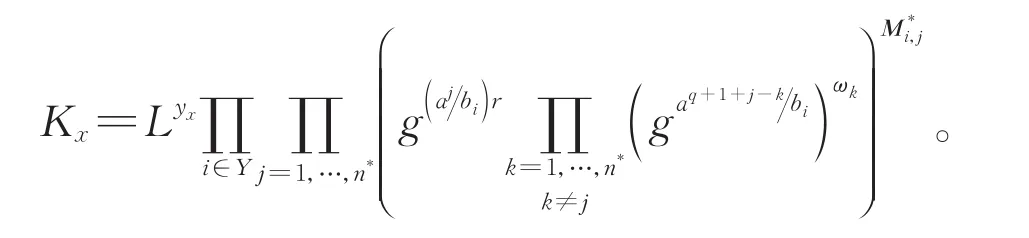
挑战阶段 最后，我们构建一个挑战密文。敌手给出两个挑战密文M0和M1，并发送给随机预言机。随机预言机掷一枚硬币β，并给出密文C=MβTe(gs，gα′)和C′=gs。

棘手的部分是模拟Ci值，因为其包含我们必须消去的项。此外，随机预言机可以选择密钥分割以此来消除这些项。直观上，随机预言机将会选择随机数y′2，…，y′n*，同时共享密钥使用向量为：

另外，其选择随机值r1′，…，rl′。

对 于i=1，…，n*，我 们 定 义 对 于 所 有 的k≠i满足ρ*(i)=ρ*(k)组成的集合Ri。换句话说，与行i具有相同属性的所有其他行索引的集合。然后生成挑战密文组成部分：

阶段2与阶段1相同。

猜测阶段 最后敌手将输出对β的猜测β′。如果β=β′，则随机预言机输出0，并猜测T=e(g，g)aq+1s；否则，如果β≠β′，则输出 1，则T为GT中的一个随机群元素。

当T是一个元组时，随机预言机B给出来看完美模拟，因此可以得到

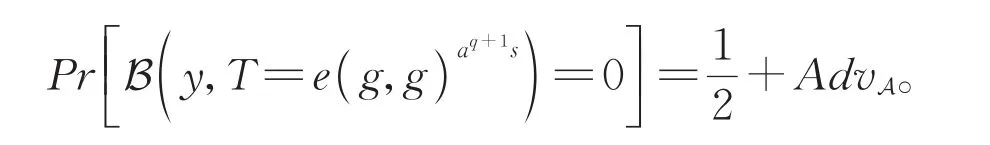
当T是随机群元素，信息Mβ对敌手是完全隐藏的，则有

因此，B可以以不可忽略的优势攻破决策性q-parallelBDHE游戏。

4 效率与安全性比较

表1中，我们总结了我们的方案和BSW加密方案及GJPS方案在密文个数和密钥大小及解密时间方面的比较。n为访问公式的大小，U为方案中定义的属性个数，nmax定义为任意访问公式的一个界值，EG表示本方案的外包解密的时间。密文的大小以组元素的数量来表示，解密时间以配对的数量来表示。

表1 本文方案与相关方案的功能和性能比较Table 1 Comparison of function and performance between proposed scheme and other related schemes

综上所述，本方案实现了与BSW加密方案相同的参数效率，但是本方案是在一个具体的安全假设下可证明安全的。同时在与GJPS加密方案相同的假设下，证明了d-BDH结构在性能方面得到了显著提升。

5 结论

本文构造了一个高效的抗合谋攻击的密文策略的可外包解密的属性基加密方案，该方案允许一个加密算法以任何访问公式来指定访问公式。我们使用线性密钥共享方案矩阵表示系统的访问控制。以前使用的结构，如公式（相当于树结构），可以用线性密钥共享方案简单表示出来。与以往使用的访问树结构描述相反，使用更通用的线性密钥共享方案表示不会损失任何效率并且可获得相同的性能和功能，并给出了该方案在一个具体且非交互模型下是可证明安全的。