基于端部磁场函数的线性感应电磁泵优化建模

张振洋， 刘慧娟， 宋腾飞， 张千， 杨立新， 毕可明

(1.北京交通大学 电气工程学院， 北京 100044； 2.北京交通大学 机械与电子控制工程学院， 北京 100044； 3.中国原子能科学研究院 反应堆工程技术研究部， 北京 102413)

环形线性感应电磁泵(annular linear induction electromagnetic pump，ALIP)[1-2]依靠结构简单、无运动部件、无需机械维修、安全可靠性高、生命周期长等特点[3]，被作为当今世界以液态金属为冷却剂的空间核反应堆动力装置循环泵的首选，俄、美两国近年来发展的各级液态金属空间核动力装置在设计上均采用了ALIP[4-9]。因此对ALIP电磁场和流体场特性的研究具有重要的理论意义和工程应用价值。

目前对ALIP基本性能的研究方法除实验外主要为解析计算和数值模拟2种。理论方面，国内外学者对于ALIP的特性解析计算主要以等效电路方法[10-11]为主，忽略或采用简单经验系数[12-16]来近似等效其纵向端部效应及铁芯饱和问题，误差相对较大。而数值计算能够一定程度弥补ALIP解析计算在端部效应及饱和问题上的不足，因此被广泛应用。Kwak[17]分析了端部效应对其泵沟中径向磁密和周向电流的轴向分布的影响，磁密在ALIP的进口处减弱，出口处增强。赵睿杰[18]基于COMSOL软件建立了ALIP 的3-D计算模型，计算了分离式定子间隙所引起的不稳定流动,计算采用28核128 G的Dell T7810工作站，单一工况耗时约18 d。Araseki等[19-22]通过数值计算和实验的方法得出纵向端部漏磁场大小和工质的速度成正相关，证实了端部效应的存在是ALIP中双倍供电频率(double supply frequency，DSF)压力脉动来源，其幅值随频率和滑差的减小而增大，采用端部梯度绕组排布能有效降低DSF脉动。

许多学者研究了端部效应对于ALIP扬程和DSF脉动的影响，而这些影响因端部效应引入的谐波力场而更加严重。网格是数值模拟的基础，而过高的网格密度会极大增加求解时间，所以往往需要采用约束边界来简化模型，ALIP泵沟内的液态金属工质是持续流动，类似于无限长结构，而仿真模型无法无限加长端部长度。因此如何建立合适的边界条件并确定合理的端部长度，既能简化模型，缩短计算时间，又能模拟真实端部效应对ALIP的影响是本文研究的重点。

本文利用Ansys-Maxwell有限元仿真软件，对一台二极三相小型ALIP建立仿真模型，对不同端部长度，不同频率，激励电流下ALIP的静态磁场分布和动态电磁场及力场分布进行计算，分析端部长度对ALIP电磁场及力场的影响，并对端部的磁场进行了数值拟合，找出端部磁场基本分布规律，确定端部磁场分布函数，从而确定最佳模型端部长度，最终通过实验验证数值模型的正确性和计算结果的准确性。

1 ALIP的基本结构与数值模型

1.1 基本结构及原理

ALIP基本结构如图1所示，其整体结构包含定子铁心、内铁芯、泵沟和励磁线圈以及环形间隙中运动的液态金属工质。定子及内铁心一般均由高磁导率硅钢片叠压而成。泵沟采用奥氏体不锈钢制作，励磁绕组线圈采用盘式铜绕组。

图1 ALIP的基本结构

当对三相绕组施加对称三相交流电时，ALIP泵沟环隙内的磁场和感应涡电流相互作用产生轴向的推力，推动工质向前流动。由于ALIP定子铁芯两端是开断的，因此会使三相绕组的电感变的不对称，引入静态纵向端部效应。当运动的液态金属流入到电磁耦合区瞬间，根据楞次定律可知，必然产生一个反向的磁场阻碍其流入，同理当工质流出电磁作用区时，也会产生一个同向的磁场阻碍其流出，这种现象称为动态纵向端部效应。

1.2 描述方程

ALIP中液态金属的流动是复杂的磁流体动力学(MHD)问题，其运动方程包含流体方程和电磁场方程。根据Navier-Stokes方程可知电磁力是作为体积力源项参与到流体运动过程中的。因此，在不考虑流体特性的前提下，基于Maxwell方程组，在忽略位移电流，引入矢量磁位A(Wb/m)后，可得液态金属中电磁场相互作用及电磁力的描述方程为：

(1)

(2)

式中：J为电流密度，A/m2；B为磁场密度，T；σ、μ分别为电导率，S/m，相对磁导率。μ0为真空磁导率；V为体积；Js为励磁电流密度；fem为电磁力密度；Fem为电磁力。

1.3 3-D有限元仿真模型

本文采用Ansys-Maxwell商用有限元软件进行ALIP的三维电磁场仿真，图2为3-D有限元仿真模型及轴向截面视图。

图2 ALIP 3-D有限元仿真模型及轴向截面视图

考虑到ALIP的中心对称特性，仿真采用周向1/6模型，并于两侧对称面加载周期对称边界条件。为模拟ALIP无限长的流体次级结构，计算区域进出口端部采用主从边界条件，满足主边界流出，从边界流入。从边界的磁场大小和方向受主边界约束。

数值模型中主要材料及几何参数如表1所示，液态金属工质为镓(Ga)，不锈钢管道采用奥氏体SUS316不锈钢，硅钢铁芯采用高磁导率的35WW350硅钢片叠压，叠压系数0.95。定子绕组采用三角形连接的盘式铜绕组，绕组排列为AAZZBBXXCCYY。

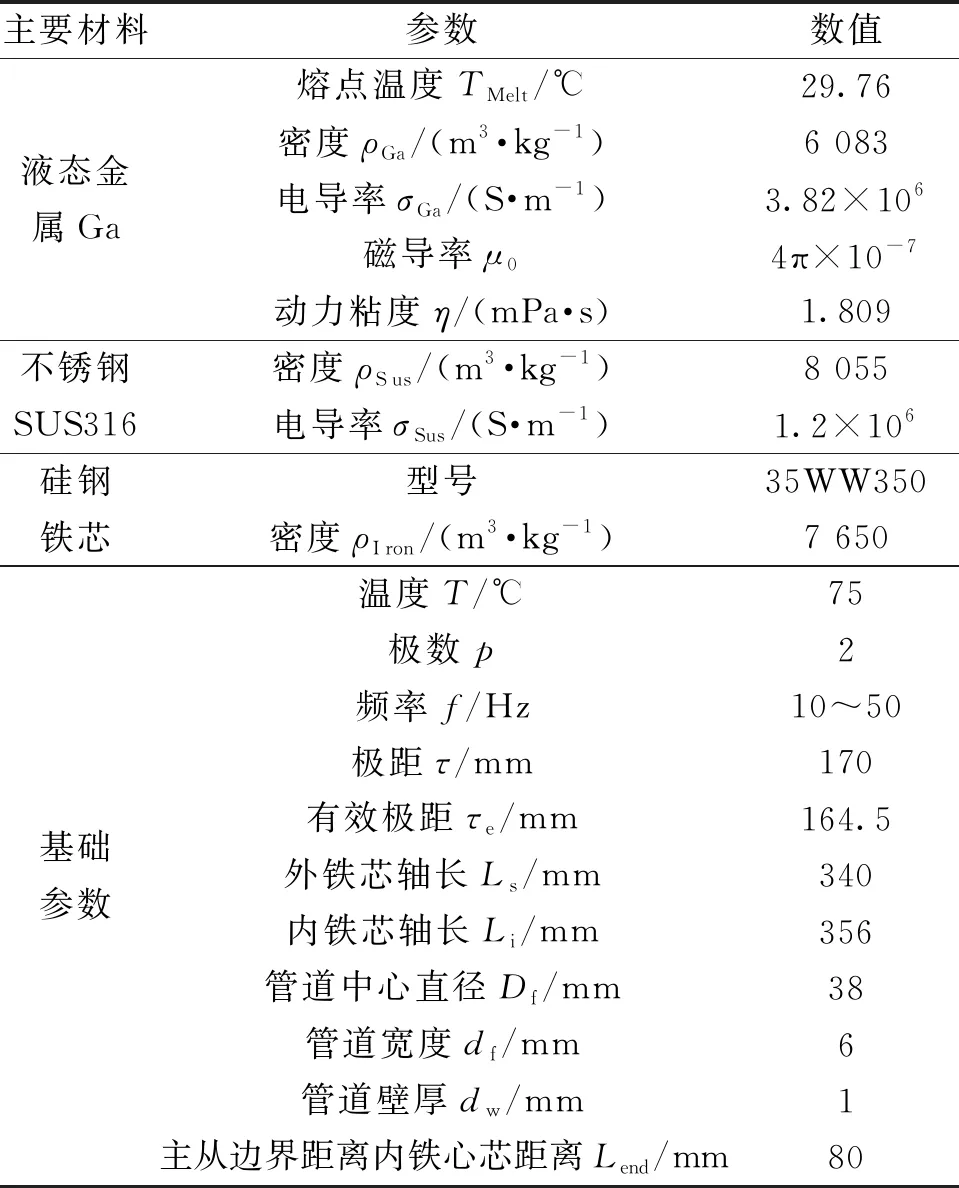
表1 基本参数

2 数值仿真结果分析

2.1 静态磁场分布

基于上述数值模型，对频率10 Hz，定子线电流44 A，管道内有无工质的静态工况进行了仿真计算，得到瞬时(t=0.2 s)磁密Br的轴向径向分布如图3所示，径向磁密幅值MagBr的轴向和径向分布如图4所示，不同径向位置的磁密幅值的轴向分布对比曲线如图5所示。

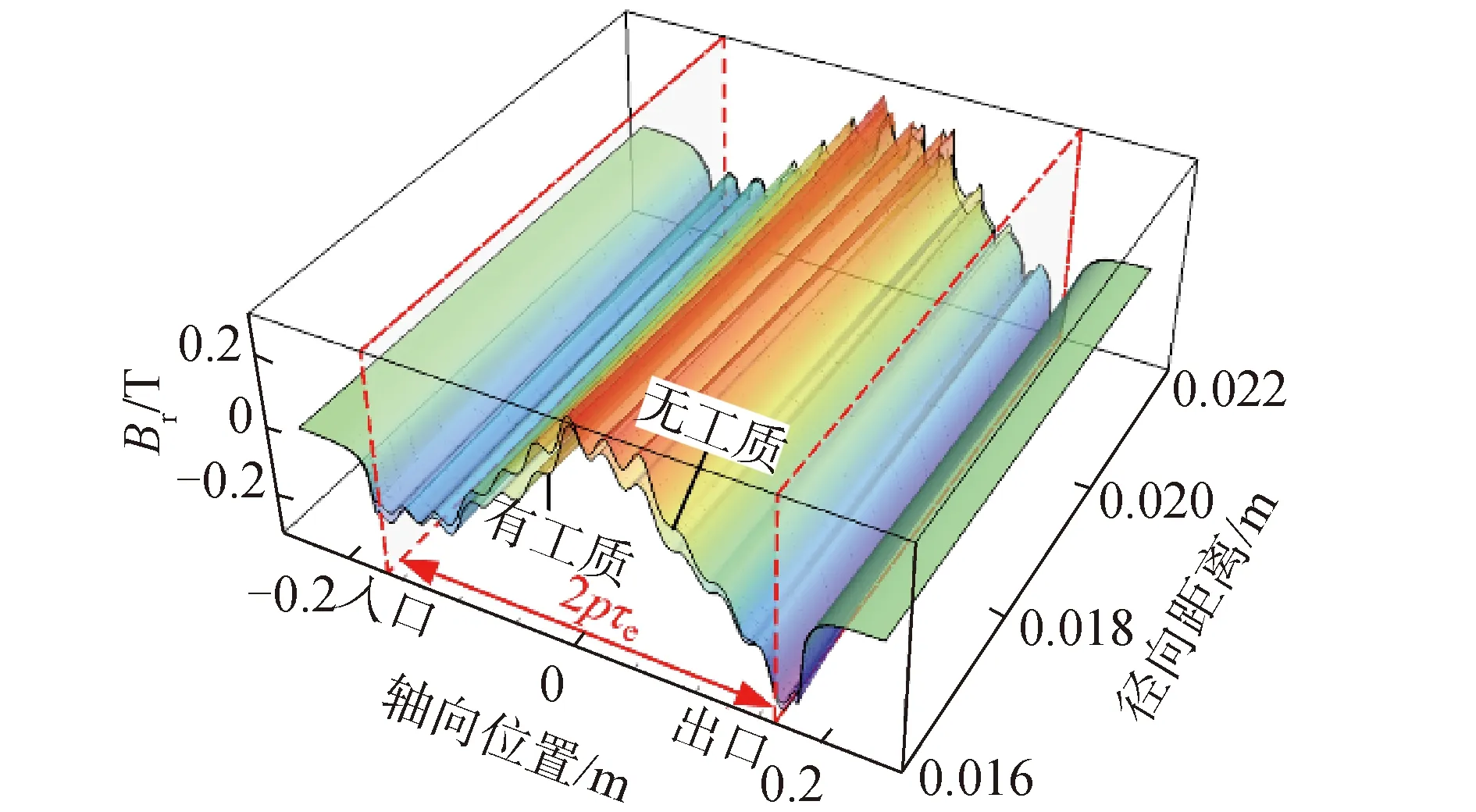
图3 流体域瞬时径向磁密轴径向分布

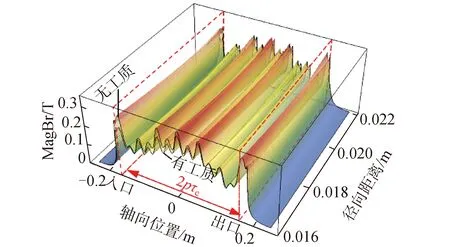
图4 流体域径向磁密幅值轴径向分布

从图3～4可知，在耦合区内，当管道内无工质时，磁场主要由励磁线圈产生，径向磁密沿中心对称分布，入口处和出口处磁场相较于耦合区中心磁场变化不大；当管道内充满工质时，其感应的涡电流会导致磁场发生畸变，从进口侧到出口侧，磁场相较于无工质时明显衰减，衰减幅度逐渐下降，在进口处附近最大，为27.86%。在出口侧，磁场相对于无工质时基本无变化，但相比于自身中心磁场明显增强，最大增长率为19.26%。由此可知，在耦合区域内，由于端部效应的影响，磁场应该含有3项分量：基波磁场、进口端部引入的前进衰减行波磁场和出口端部引入的后退衰减行波磁场。其中前进行波磁场与基波磁场符号相反，起削弱作用，衰减慢，衰减距离长，对磁密影响较大，后退行波磁场与基波磁场符号相同，起增强作用，衰减快，衰减距离短，对磁密影响较小。

对比图5中有无工质下的曲线可知，不同径向位置的磁密分布规律基本相同，在耦合区域沿轴向均存在一定的脉动，当半径为16 mm时，即离内导磁铁心最近，其磁密最大，随着半径增加，漏磁增多，磁密逐渐衰减，当定子齿一侧即径向距离22 mm时，径向磁密最小，而且在定子槽的位置会产生一个凹槽状波谷，这主要是齿槽效应导致气隙磁导不均匀而产生的空间谐波引起的。

图5 流体域不同径向位置磁密幅值对比曲线

在入口区域和出口区域内，由图4～5均可看出，不管磁场是被削弱还是增强，其端部磁场在轴向上向外侧均呈现衰减趋势，衰减速率先增大后减小，虽然磁场衰减较快，但是进出口衰减距离(磁场从衰减开始到衰减为10-3T的距离)均约为44.52 mm，占有效极距的27.1%，并非远远小于极距，所以对端部磁场进行计算分析是十分必要的。

2.2 负载工况下电磁场及力场分布

由静态磁场的分析可知，流体域中磁场在径向位置上虽然逐渐衰减，但其轴向的分布基本相同，为进一步研究瞬态负载过程中，流体域端部磁场对于涡电流和电磁推力的影响，以r=19 mm为观测位置，对频率10 Hz，定子线电流44 A，平均流速1.7 m/s的负载工况进行了数值仿真，得到流体域的磁场密度、涡电流密度和电磁力体密度的周期时域内轴向分布分别如图6～8所示。

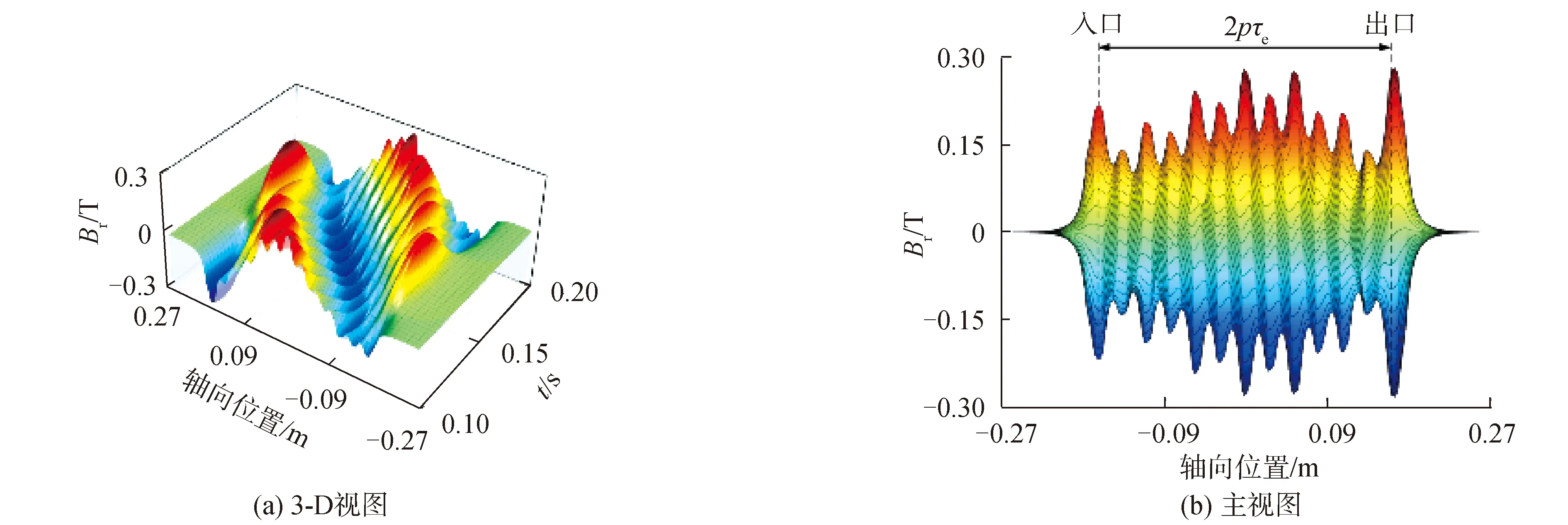
图6 周期时域内流体域磁密轴向分布

根据图6 (a)和图7(a)的3-D视图可以看出，在确定的轴向位置，磁密和涡电流密度沿时间轴均为一系列幅值不同的周期性正弦函数，其中幅值沿轴向分布分别为图6(b)、图7(b)中的包络线外边界的绝对值。在确定的时间点上，磁密和电涡流密度沿位置轴均呈现两极分布，根据其图6(b)时域包络线可以看出端部效应的存在对磁场的影响与静态场工况是完全一致。图7(b)中进出口外侧电涡流密度并未像磁密一样逐渐衰减至零，而是最终稳定在一个较小的值不再变化，这主要是因为工质导电的原因，其电涡流密度并不会衰减至零。

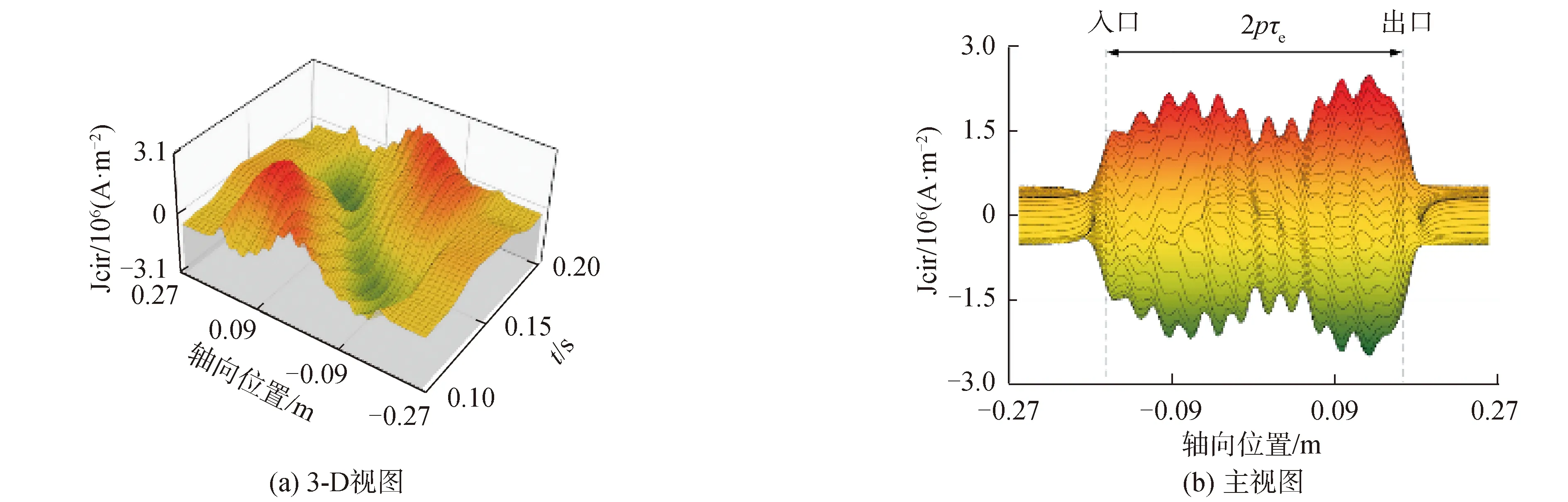
图7 周期时域内流体域电涡流密度轴向分布

由于磁场和电涡流均为正弦函数，根据式(2)可知，电磁力密度除含有稳定的直流分量外，必然还存在一个频率为双倍供电频率的周期瞬时分量，如图8(a)、图8(c)所示。因此ALIP的DSF压力脉动现象，本质上是电磁力中所含有的特有周期分量所引起的。根据图8(b)可知，在耦合区内，电磁力密度基本为正，产生驱动力，而在端部进口区域和出口区域外侧，电磁力密度均基本为负，产生阻力。在耦合区中心向两侧端部靠近的过程中，因端部磁场前进和后退分量引入的阻力密度的影响，其电磁力密度逐渐下降，到进出口位置达到负向最值，然后逐渐衰减回零。对比进出口侧的影响可知，进口处负向最值的绝对值较小，而进口侧对于耦合区影响距离较长，出口处负向最值的绝对值较大，而出口侧对于耦合区影响距离较短，但二者相对于耦合区总的力密度而言，其影响均不可忽略。

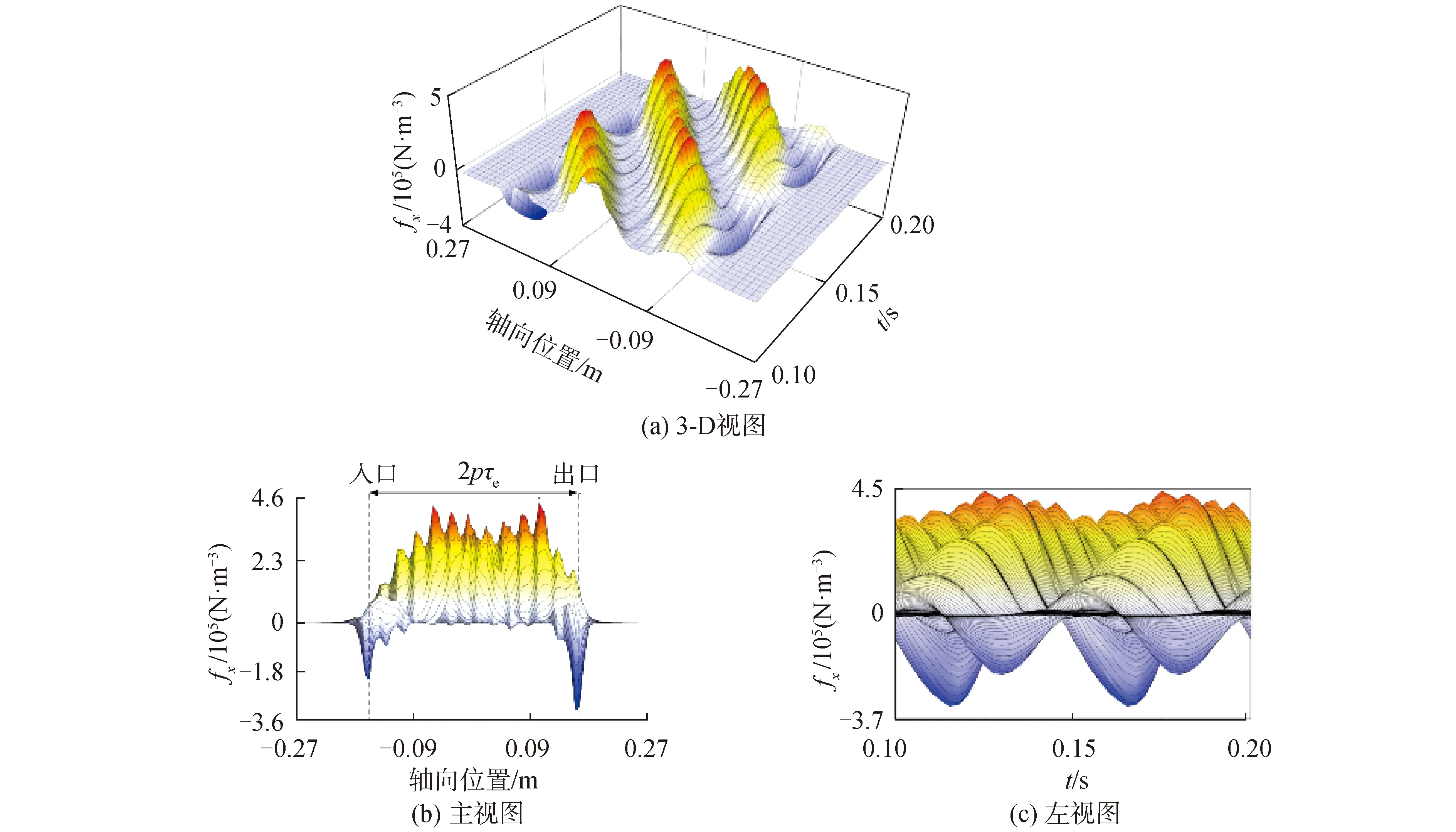
图8 周期时域内流体域电磁力密度轴向分布

2.3 不同端部长度对电磁场及力场的影响

数值模拟时，端部边界条件是其求解有限元差分方程的重要条件，合理的端部边界既能体现出其特有的端部效应又能节约计算资源。本文采用主从边界进行无限长流体次级的简化，并针对不同端部长度(Lend)的数值模型进行了仿真，研究不同Lend对ALIP的电磁性能的影响，得到以下仿真结果。

图9、图10分别为频率10 Hz、线电流44 A、流速1.7 m/s、时间0.15 s时，流体域中磁密和电磁力密度在不同Lend下的对比曲线。

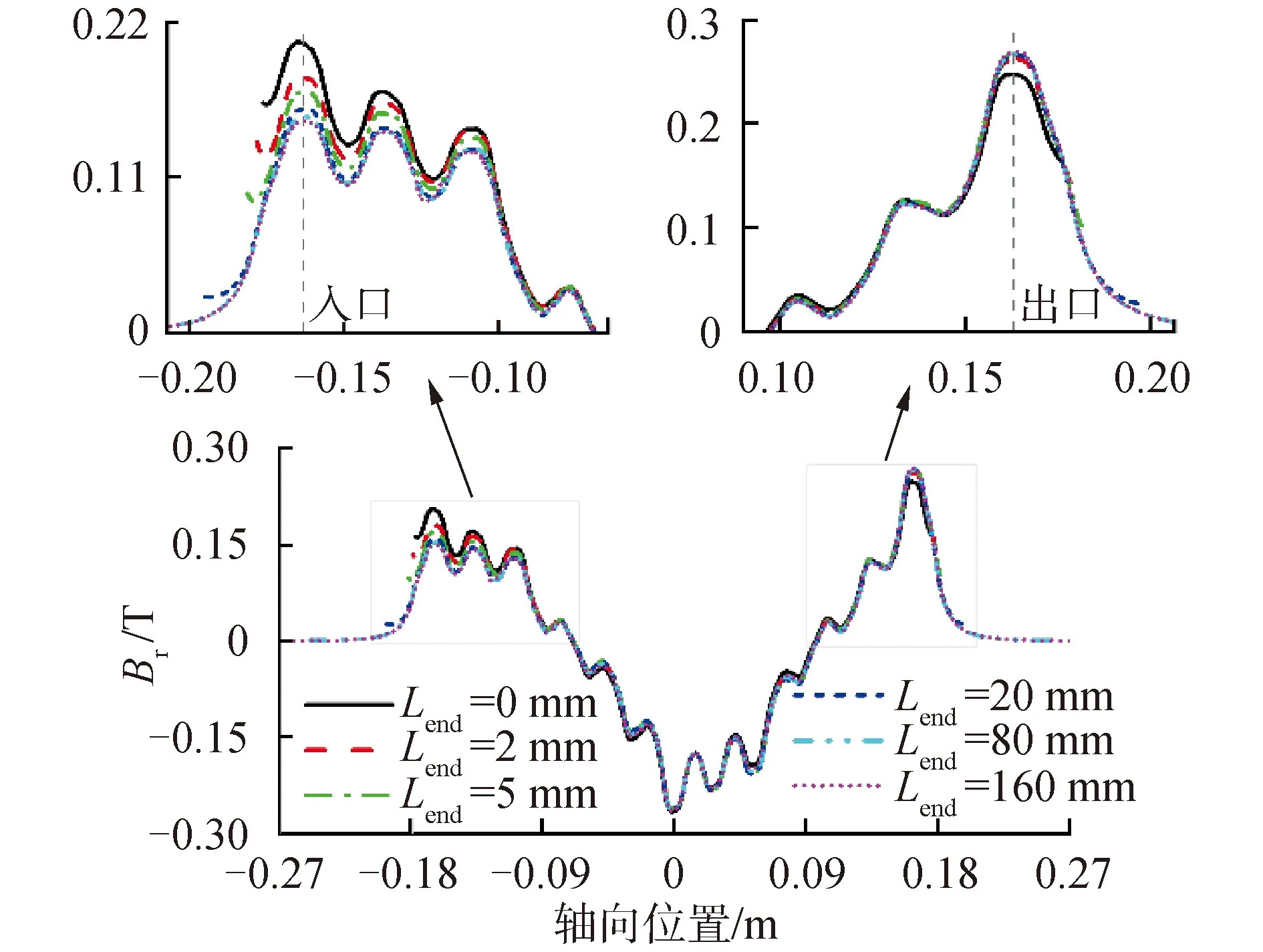
图9 不同端部长度下磁密对比曲线(10 Hz)

如图9所示，频率为10 Hz时，随着Lend逐渐增加，在靠近进出口处位置，Lend越大，端部效应越明显，但当Lend增大到一定值(Lend=80 mm)后，继续增加，其磁密分布基本不再变化；在耦合区中心位置附近，磁密变化幅度相对较小。由于力密度为径向磁密Br和周向涡电流密度Jcir的乘积，显然在图10中可以看出，Lend的变化对力密度fx的轴向分布的影响在整个轴向位置均有体现，当Lend大于80 mm时，fx的分布也逐渐趋于稳定。

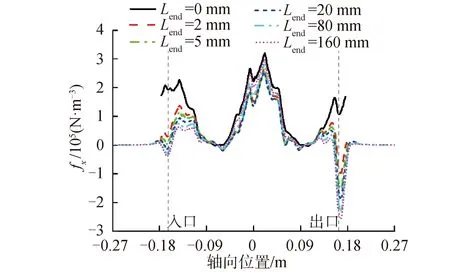
图10 不同Lend下电磁力密度对比曲线(10 Hz)

图11、图12分别为频率50 Hz、线电流44 A、流速1.7 m/s、时间0.115 s时，流体域中磁密和电磁力密度在不同Lend下的对比曲线。图13为线电流44 A、流速1.7 m/s时，10 Hz与50 Hz对应的不同Lend下的电磁压差对比曲线。

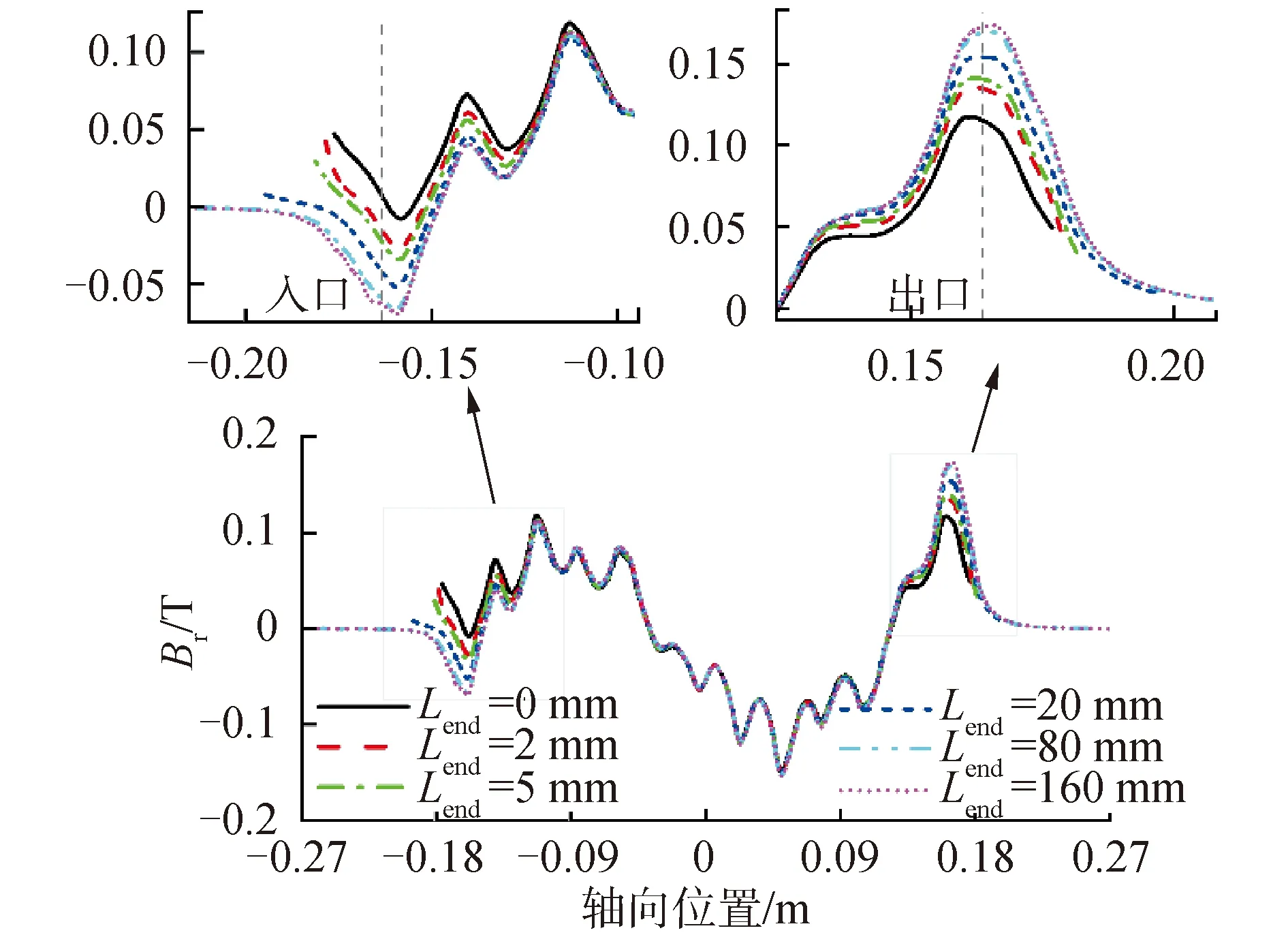
图11 不同Lend下磁密对比曲线(50 Hz)

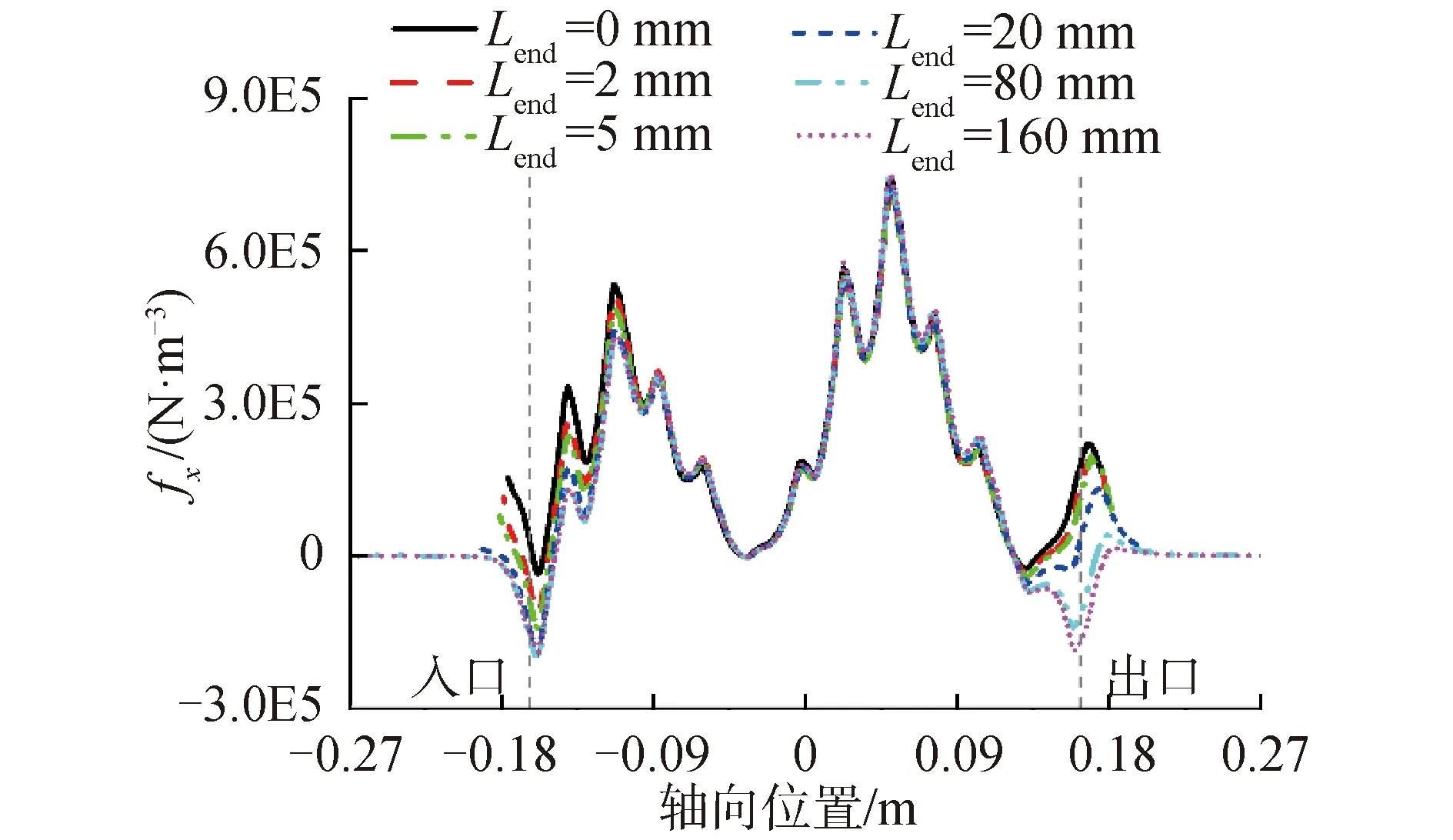
图12 不同Lend下电磁力密度对比曲线(50 Hz)

对比50 Hz工况和10 Hz工况下的Br和fx分布可知，Lend不仅影响进出口区域电磁特性参数，而且对耦合区也有一定的影响。在进出口端部区域，Lend对电磁场和力场的影响规律与频率无关，均是随Lend的增加，端部效应愈加明显，当在Lend大于80 mm时趋于稳定；而在耦合区内，受端部效应影响的轴向范围随f增大有所减小。从图13可以看出，随Lend增加，ALIP端部效应越明显，电磁压差逐渐减小至稳定，DSF压力脉动逐渐增加至稳定。因此可以通过改善端部效应降低DSF压力脉动，提升ALIP的性能。

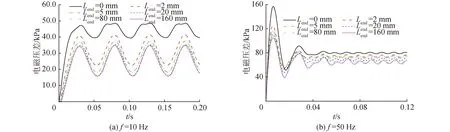
图13 不同Lend下电磁压差对比曲线

3 端部磁场拟合及分布规律

考虑到ALIP数值模型的电磁性能计算结果的精确度及端部效应对其的影响随端部长度的增加而更加准确，而且存在一个临界Lend使其电磁特性参数的计算结果达到收敛，因此在数值模拟时可以通过拟合端部磁场衰减分布规律，建立分布函数，进而确定端部磁场的衰减距离，得到其最佳Lend。

在直线电机中，定子铁心开断处磁密向外衰减规律基本符合一阶指数形式，考虑到ALIP的内铁芯在两侧比初级铁芯长出一段距离，因此本文采用一阶和二阶两类指数函数进行端部磁场的模拟。

图14为不同频率下，进出口端部磁密幅值的拟合曲线图，其中散点为仿真值，实线代表一阶指数拟合曲线，线段代表二阶指数拟合曲线。图中各频率所对应的一阶和二阶指数拟合函数的具体参数如表2所示。

图14 不同频率下进出口区域轴向磁密拟合曲线

从图14可以看出，在有铁芯衰减区段，端部磁密的仿真值衰减速率逐渐增加，在内铁芯端部位置达到最大，然后进入无铁芯衰减区段，衰减速率逐渐减小。一阶指数函数拟合结果在有铁芯区段，其趋势和仿真结果相反，数值相差较大，在无铁芯位置区段，趋势相同，但仍存在较大误差。二阶指数函数拟合结果在有铁芯段，趋势和数值都与仿真结果较为吻合，但在无铁芯段，衰减速率下降过快，存在一定的偏差。

从表2的拟合参数值来看，无论一阶还是二阶指数函数拟合，虽然随频率变化，其端部磁场的最大值发生变化，但其一阶和二阶指数拟合函数的衰减因子在一定误差范围内基本保持不变，因此可以说明端部磁场的衰减的规律受频率影响较小。

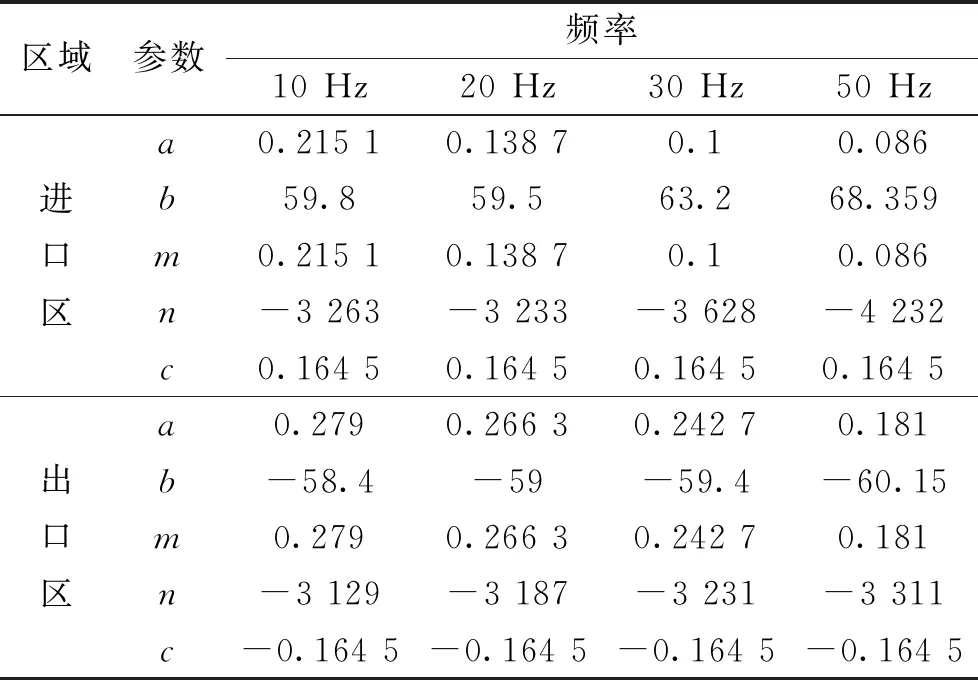
表2 不同频率下端部区域磁密拟合曲线参数表

图15上图为频率10 Hz，线电流44 A时不同转速工况下，磁密幅值的轴向分布曲线，图15下图为不同速度下端部平均磁密的一阶和二阶指数函数拟合曲线。因ALIP流体损耗特性的影响，其工作转差较大，一般大于0.5，所以数值仿真只给出转差大于0.5速度工况。从图15(a)中可以看出，在进出口端部区域内，端部磁场衰减分布受转速影响不大。图15(b)中一阶和二阶指数函数的参数值与表2中拟合参数基本相同。由此可说明端部衰减磁场分布规律受转差影响不大。

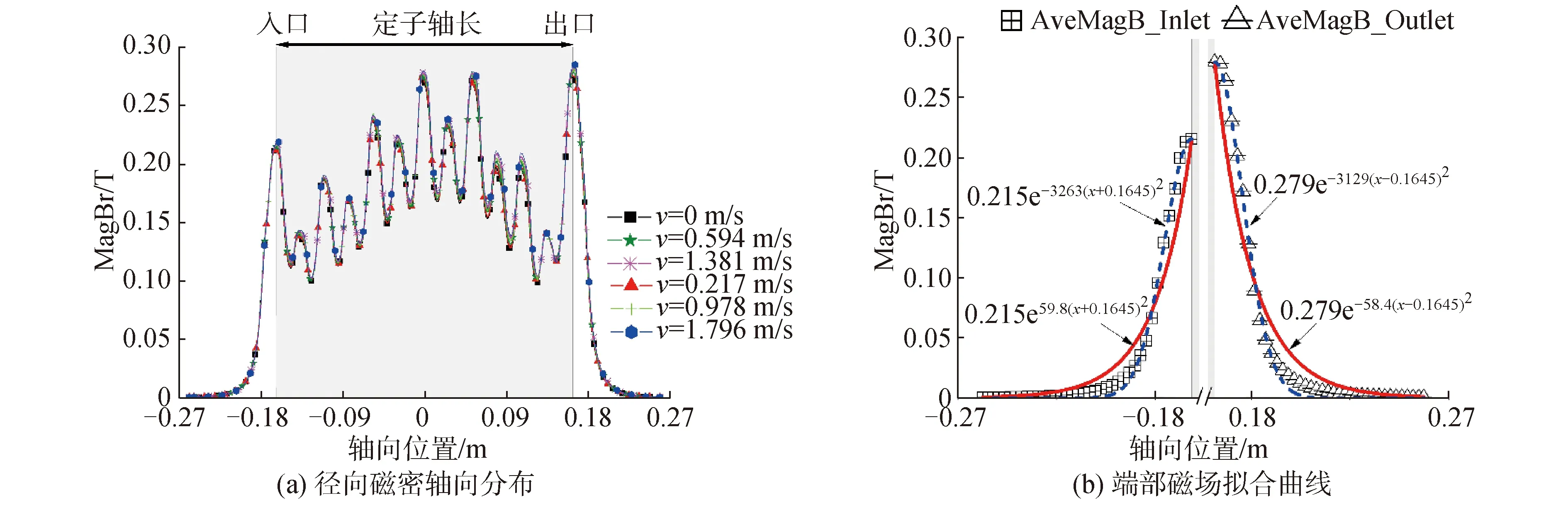
图15 不同速度下径向磁密轴向分布及端部磁场拟合曲线

根据一阶和二阶指数函数的拟合结果分析可知，在有铁芯区域，二阶指数拟合相对精准，在无铁芯区域，一阶指数拟合更有效，但由于二者分别在有无铁芯段均存在一定的误差，所以无法单独通过其拟合函数表达式求解出合理的端部长度值。因此本文根据端部磁场的分布特性，采用分段函数的形式进行拟合。进出口区域内的分段拟合函数分别为：

(3)

(4)

采用自定义的分段拟合函数对线电流44 A，不同频率工况的进出口端部磁场进行了拟合，拟合结果如图16所示，可以看出分段拟合曲线和仿真数据具有很好的一致性。

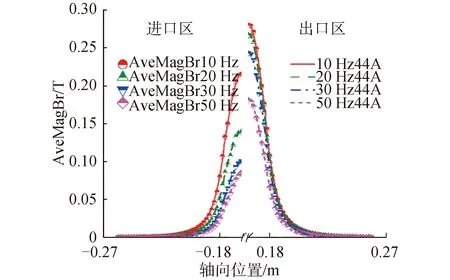
图16 不同频率下端部磁密自定义分段拟合曲线

各拟合曲线的具体参数值如表3所示。从表3可以知，在无铁芯段，一阶指数拟合函数的进出口衰减因子随ai(o)的降低略微有所上升，但最大误差均在1.5%以内，可以认为衰减因子基本保持不变，取其4种工况下bi的平均值为116，bo的平均值为112.4，二者误差约为3%，故可认为进出口衰减因子相同，约为114.2。

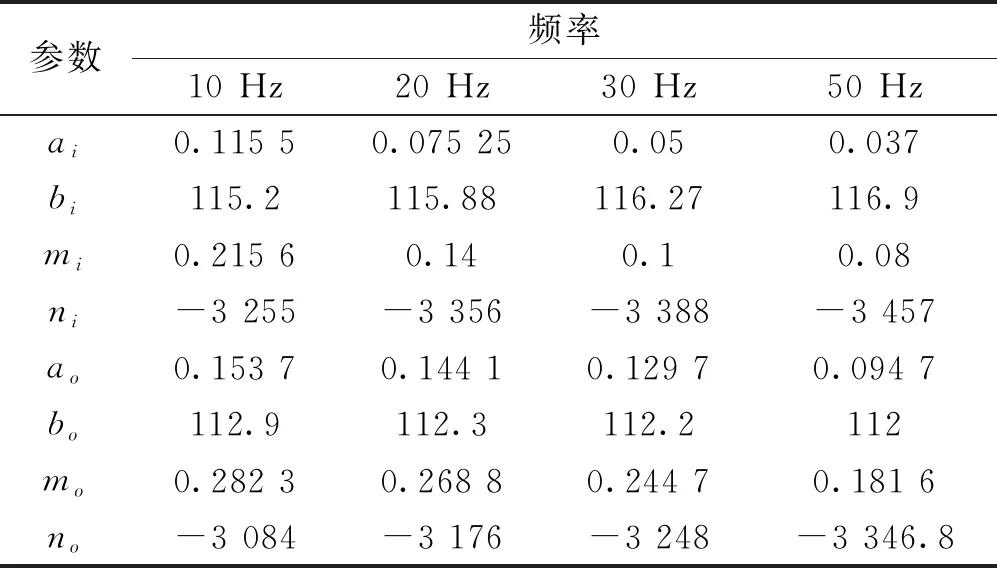
表3 不同频率下端部磁密自定义分段拟合曲线参数表

在有铁芯段，二阶指数拟合函数的进出口衰减因子随mi(o)的增大而增大，最大误差为12.1%，相比无铁芯段误差较大，这主要是由于在有铁芯段，开始衰减的半个齿的范围内，定子铁芯和内铁芯均存在，其磁密近似无衰减所导致的。

考虑到端部衰减距离采用无铁芯段的一阶指数拟合函数反向求解即可，所以有铁芯段二阶拟合函数虽然误差相对较大，但并不影响最终求解出合适的端部长度Lend。因此将一阶拟合端部衰减因子带入到式(5)和(6)，可以得出端部磁密衰减到10-4T时的衰减距离为67.6 mm，衰减到10-5T时衰减距离为87.1 mm，考虑到磁场密度小于10-4T后磁密已基本可以忽略，因此只要端部长度Lend大于67.6 mm，数值模型的计算结果就可以准确模拟出ALIP的电磁性能和端部效应对电磁泵的性能影响。

4 实验对比

基于端部磁场拟合函数，文中数值模型的端部长度Lend取80 mm，并对优化后模型进行了仿真计算，为进一步验证数值模型和计算结果的准确性，搭建了试验回路，其3-D示意图如图17所示，对ALIP在不同频率和电流工况下的关阀静态压头进行测试，最终得到的实验与数值仿真对比结果如图18所示。

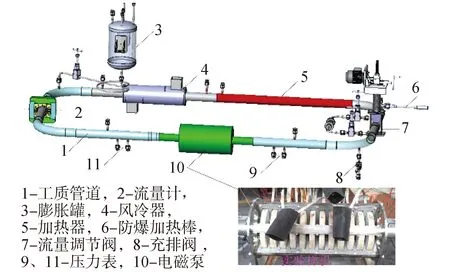
图17 ALIP实验回路示意

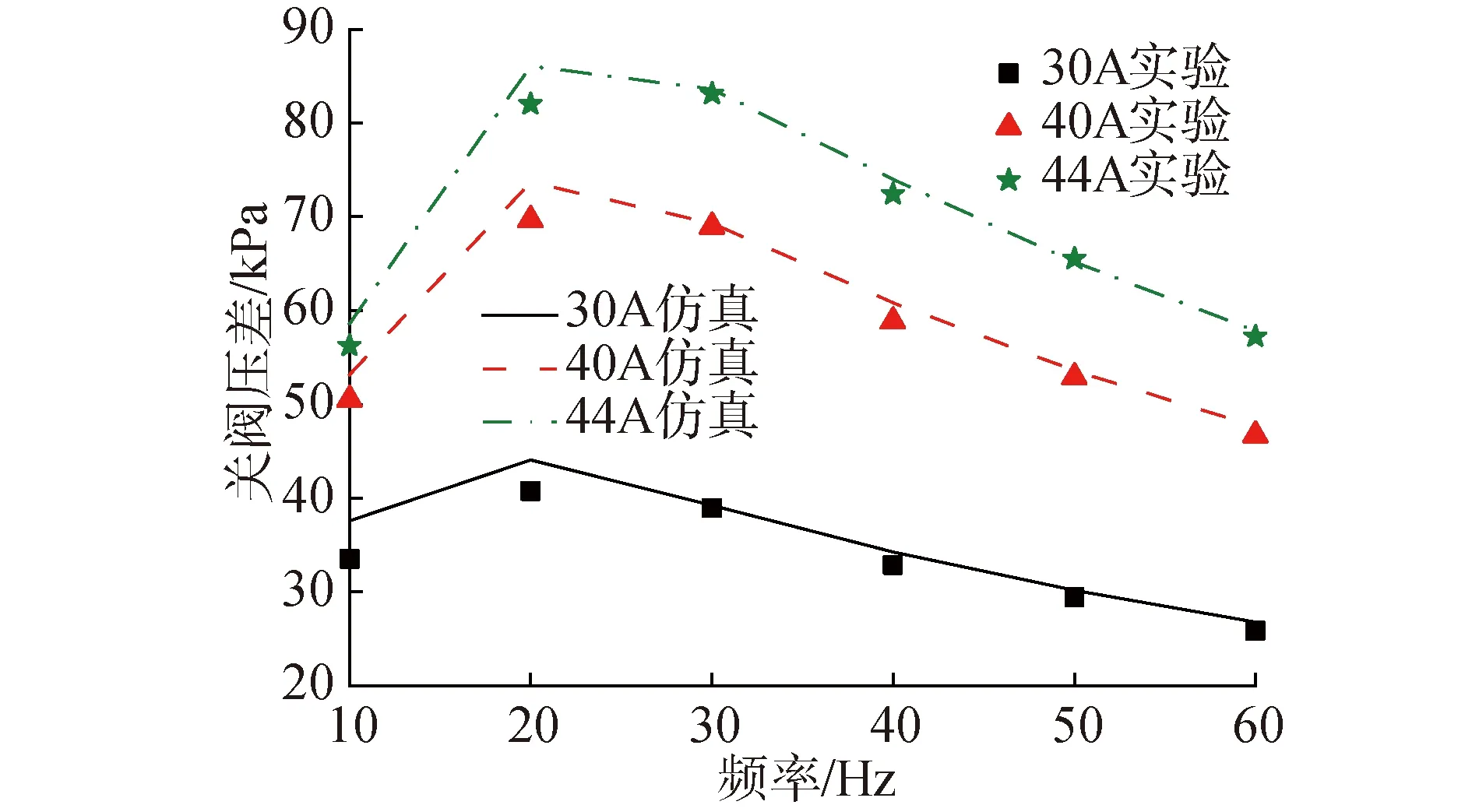
图18 不同频率电流时实验与仿真关阀压差对比曲线

从图18可以看出，仿真结果和实验数据具有很好的一致性，其中最大误差9.2%，其余误差基本在6%以内。因此采用主从边界条件条件，端部长度Lend=80 mm的数值模型计算结果具有较高的可靠性和精度，同时说明通过端部拟合函数优化数值模型，缩短求解时间，提升求解结果准确度的方法是行之有效的。

5 结论

1)ALIP的耦合区磁场含有3个分量，基波磁场，沿运动方向衰减的前进行波磁场，沿与运动方向反向衰减的后退行波磁场。其中前进行波磁场与基波磁场符号相反，使入口处磁场减弱，呈现入口端部效应，后退行波磁场与基波磁场符号相同，使出端磁场增强，出口处磁场增强，呈现出口端部效应。

2)存在一个临界的Lend值，在小于临界值范围，ALIP电磁场和力场的端部效应随着端部长度Lend的增加而愈加明显，在大于临界值范围，其分布基本不再随Lend的增加而变化。

3)ALIP的非耦合区两侧端部磁场沿轴向向两侧衰减，衰减规律受频率，转差影响较小。在有铁芯位置，衰减规律符合二阶指数函数分布，无铁芯位置符合一阶指数函数分布，通过逆向求解分布函数可以确定其衰减距离，进而确定临界端部长度，即数值模型的最佳端部长度。

4)实验结果和采用最佳端部长度的数值模型计算结果具有较好的一致性，最大误差9.2%，其中87%的结果误差在6%以内，验证了数值模型的正确性和计算结果的准确性。