故障滚动轴承的非线性动力学建模与振动分析

郑龙魁， 向阳， 盛晨兴

(武汉理工大学 能源与动力工程学院，湖北 武汉 430000)

旋转设备已广泛应用于社会的各行各业中，并发挥着越来越重要的作用，滚动轴承是旋转设备的关键部件之一，其动力学特征直接影响到旋转设备的运行质量。随着社会的不断发展，旋转设备对轴承等设备的动力学特性、稳定性及精确度的要求越来越高，虽然人工智能的崛起，提高了故障诊断的精度和诊断的效率，但是为了能更好地理解轴承故障的机理机制和更有效率地研究故障滚动轴承的振动特性，建立滚动轴承的非线性动力学模型具有非常重要的意义[1-4]。

目前国内外已有很多学者研究了滚动轴承的动力学模型。Petersen等[5]建立了双列滚动轴承的动力学模型，研究了轨道具有不同深度、不同长度的故障时，轴承的准静载荷分布情况和刚度变化规律，分析表明当滚动体经过故障位置时，由于内圈与滚动体之间的接触力将重新分配，所以滚动体刚度在加载方向减小，在卸载方向增加，还分析了滚动体经过故障位置时静载荷力的波动，该方法的时频响应具有较好的周期性和规律性。Upadhyay等[6]建立了滚动轴承的非线性动力学模型，研究了滚动体直径变化和滚动体个数变化时对高速旋转轴的非线性振动的影响，建模过程中滚动体与内外圈之间的刚度是非线性变化的，并添加了阻尼的影响，Newmark-β方法被用于求解动力学模型，结果表明当滚动体个数增加时意味着增加了系统的硬度，其可以减少BPF (ball passing frequency)的影响。Ahmadi等[7]建立了故障轴承的非线性动力学模型，分析了线剥落故障与滚动体接触时的振动特性，在建立动力学模型时考虑了滚动元件的有限元尺寸，提高了模型预测故障振动响应的精确度。刘倩楠等[8]建立了外圈剥落时具有双冲击现象的轴承动力学模型，主要分析了滚动体与剥落区域的接触特征，与实测数据相比较时该模型可以有效地计算出轴承剥落故障时的时频响应。姚廷强等[9]基于多体系统动力学理论、Hertz接触理论、轴承间隙、齿轮侧隙以及载荷工况等因素，提出了球轴承-螺旋锥齿轮系统的分析方法，分析了轴承和齿轮的特征频率的振动响应及影响规律。Singh等[10]研究了局部线性剥落故障时轴承的振动响应，建立了故障轴承的有限元模型，采用显示动力学有限元软件LS-DYNA (LS-Dynamic)对所建立的有限元模型进行仿真计算，将仿真得到的结果进行了信号预处理，结果表明该有限元仿真方法可以有效地计算出故障轴承的时频特征，进而证明了该方法的有效性。Harsha[11]建立了滚动体与内外圈非线性刚度连接的动力学模型，介绍了非线性刚度的取值方法，分析了水平和垂直方向的时频特征及其振动规律，剖析了Poincare映射的周期性运动，但是该方法的坐标选取复杂，没有研究故障时轴承振动响应。

以上文献都对滚动轴承的动力学模型进行了研究，但很少有学者是从转动速度的角度去分析故障轴承的振动特点，本文将从转速的角度去建立故障区域的冲击激励，其过程是将故障区域的接触特征与滚动轴承的转速相结合，建立滚动体与故障区域之间的冲击激励公式，该公式可有效反映出转速对故障冲击激励的影响。采用Hertz接触理论求得滚动体与内外轨道之间的非线性刚度系数，并推导出轴承各部件的能量贡献公式，进一步，基于拉格朗日方程建立了以质量-弹簧表示的故障滚动轴承的非线性动力学模型，并进行了试验验证。

1 轴承的相关参数

滚动轴承的二维振动模型如图1所示，将复杂的滚动轴承系统简化为质量-弹簧系统，其中外圈固定在轴承座上，内圈固定于转轴上，随转轴的旋转而旋转。加载后内圈会发生一定距离的偏移，此时滚动体与内外圈相的接触符合Hertz接触理论。αj是第j个滚动体的角位置，θ是由保持架控制的2个滚动体之间的间隔角度，其与滚动体的个数有关，它们的表达式分别为[12]：

图1 滚动轴承的二维振动模型

(1)

(2)

式中：φ0是初始相位角；ωball是滚动体的公转角速度；Nb是滚动体的个数；t是时间。

由于轴承振动非常复杂，在建立轴承的动力学模型时应满足以下假设：1)滚动体、内外圈和转轴在同一平面内运动；2)滚动体无打滑现象；3)不考虑阻尼的影响。

当受到外界作用力时，根据赫兹接触定理可知，轴承中滚动体与内外圈的接触属于非线性的弹性接触，其接触面呈现出椭圆的形状，滚动体与内外圈接触的非线性刚度系数可由式(3)计算[11-12]：

(3)

式中：Ki表示滚动体与内圈接触的刚度参数；Ko表示滚动体与外圈接触的刚度参数；δi和δo分别是滚动体与内外圈的接触变形量。

内外圈接触的刚度参数分别与内外圈轨道的曲率和∑ρi、曲率差有关，曲率和、曲率差可由轴承本身的尺寸参数计算得出，因此轴承整体的有效的非线性弹性模量K由内圈的弹性模量计算得到：

(4)

式中对球轴承n=3/2。

利用拉格朗日方程可以比较简单地推导得到用广义坐标(ρ、x、y)表示的轴承振动系统的运动微分方程[13-14]，拉格朗日方程可以表示为：

(5)

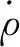
T=Tr.e.+Ti.r.+To.r.+Trotor

(6)

式中：Tr.e.是滚动体的动能；Ti.r.是内轨道动能；To.r.是外轨道动能；Trotor是转子动能。

V=Vr.e.+Vi.r.+Vo.r.+Vrotor+Vs

(7)

式中：Vr.e.是滚动体的势能；Vi.r.是内轨道势能；Vo.r.是外轨道势能；Vrotor是转子势能；Vs是滚动体与轨道间的弹性势能。

图2是加载后轴承的局部放大图，其中αj是第j个滚动体中心加载前的角位置(如图1所示)；αoj和αij分别是加载后第j个滚动体中心与外、内轨道中心的角位置；Kin和Kout分别是滚动体与内外圈的接触刚度；ρj和χj分别是承载后滚动体中心到外圈中心和内圈中心的距离；Min和Mout分别为内外圈的质量中心；Mball是滚动体的质量中心。加载后内圈质量中心发生偏移现象，设偏移距离分别表示为xin和yin，外圈固定在轴承座上，所以外圈质量中心不发生偏移，第j个滚动体质量中心偏移后的位置用ρj和αj来表示。

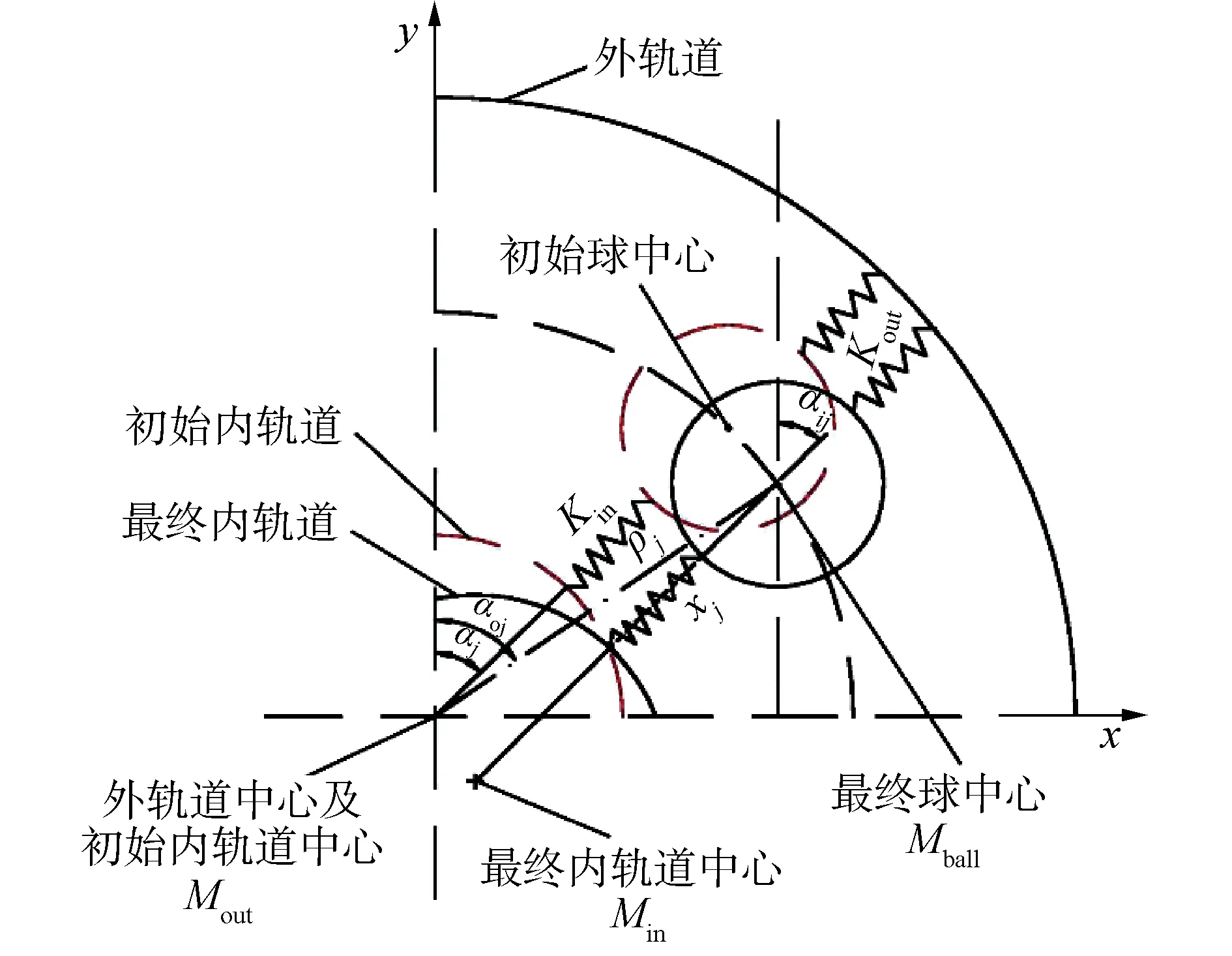
图2 滚动轴承的弹簧质量模型

1.1 滚动体的动能与势能

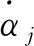
(8)

式中：mj是第j个滚动体的质量；φj第j个滚动体的转动惯量；ρj是第j个滚动体的位移向量，其表达式为：

ρj=(ρjsinαj)i+(ρjcosαj)j

(9)

经化简整理得：

(10)

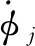
(11)

式中：R是轴承外轨道半径；ρr是滚动体半径。

因此第j个滚动体的动能表达式为：

(12)

Nb个滚动体的总动能和总势能分别表示为：

(13)

(14)

1.2 内圈和转轴的动能与势能

轴承加载后分别用xin和yin分别表示x方向和y方向上的偏移距离，转轴和内圈具有相同的偏移距离，内圈和转轴的位移矢量公式为：

rin=xini+yinj

(15)

对其进行求导及平方后整理可得内圈的动能为：

(16)

内圈相对于坐标系原点的势能变化为：

Vi.r.=mingyin

(17)

同理，转轴的动能和势能分别为：

(18)

Vrotor=mrotorgyin

(19)

式中：min是内圈质量；Iin是内圈转动惯量；mrotor是转轴质量；Irotor是转轴转动惯量。

1.3 外圈的动能与势能

外圈固定于轴承坐上，外圈的质量中心点不发生任何变化，因此外圈的动能和势能均为0，即To.r.=0,Vo.r.=0。

1.4 弹性接触的势能

轴承工作时，滚动体与内外圈的接触是一种符合赫兹接触定理的非线性连接，该弹性势能为：

(20)

式中：δin是滚动体与内圈的接触变形量；δout是滚动体与外圈的接触变形量。δin和δout的分别表示为：

(21)

式中：r是内轨道半径；ρr滚动体半径；χj内圈质量中心到滚动体中心的距离。

(22)

式中：R为外轨道半径；ρj为外圈质量中心到第j个滚动体中心的距离；γ0为轴承中滚动体和内外圈之间的间隙如图2所示。

由图2可知，第j个滚动体到内圈质量中心距离χj与广义坐标xin、yin和ρj的关系式：

(23)

根据式(23)可推导出相关参数的表达式。

2 轴承的碰撞冲击方程

图3(a)展示了轴承外圈故障的示意图，当轴承外圈发生故障时，滚动体经过故障区域可分为3个阶段：1)滚动体即将进入故障区域；2)滚动体处于故障区域中；3)滚动体即将离开故障区域。根据参考文献[15]可知：滚动体从阶段2进入阶段3的过程对轴承振动的影响最大，该过程将产生一个作用时间较短(突然增大而后迅速消失)、量值较大的冲击力Fco，其表达式为：

图3 轴承故障模型

(24)

式中：m为滚动体的质量；tb为碰撞时间；vball为保持架的转动速度，其可以表示为：

vball=ωball·dm

(25)

式中dm是轴承的节圆直径。

设相对于x轴的外圈故障中心的角位置为βo(0°≤βo≤360°),故障范围用β表示见图3，即滚动体与故障区域所产生的冲击方程可以表示为：

(26)

式中 mod是取余函数。

同理，当轴承内圈发生故障如图3(b)所示，β1是内圈故障的角度范围，滚动体与内圈故障接触的流程与外圈的流程相同。滚动体从阶段2进入阶段3的也将产生一个作用时间较短(突然增大而后迅速消失)、量值较大的冲击力Fci[15]。由于内圈和滚动体均有转动速度，因此冲击力Fci不仅与滚动体的转速度有关，还与内圈的转速有关，其表达式为：

(27)

式中vi为内轨道的转动速度。因此内圈故障时，冲击方程可以表示为：

Fi=

(28)

式中：ωin为内圈角速度；t为轴承运行时间；ωball为保持架的角速度。

3 故障轴承的动力学方程

将式(13)～(14)、(16)～(20)、(26)和(28)分别代入式(5)～(7)中可得故障轴承的动力学公式：

1)外圈故障：

(29)

2)混合故障：

(30)

4 仿真及实验验证

以6206深沟球滚动轴承为研究对象，采用Newmark-β方法求解非线性动力学方程组。6206轴承的几何参数见表1，设置相关参数：γ0取值为0.001 mm；滚动体的初始位置(ρj)为22 mm；仿真步长0.000 1 s；内圈的初始偏移量xin和yin均为10-3mm；外部加载力(W)取值50 N；βo=270；碰撞时间tball=0.001； s；仿真速度分别为21 rad/s和42 rad/s。图4是专门设计的故障轴承试验台，该试验台由三向异步电机、扭矩传感器、减速齿轮箱、偏心轮、试验轴承、磁力制动器以及联轴器等组成。

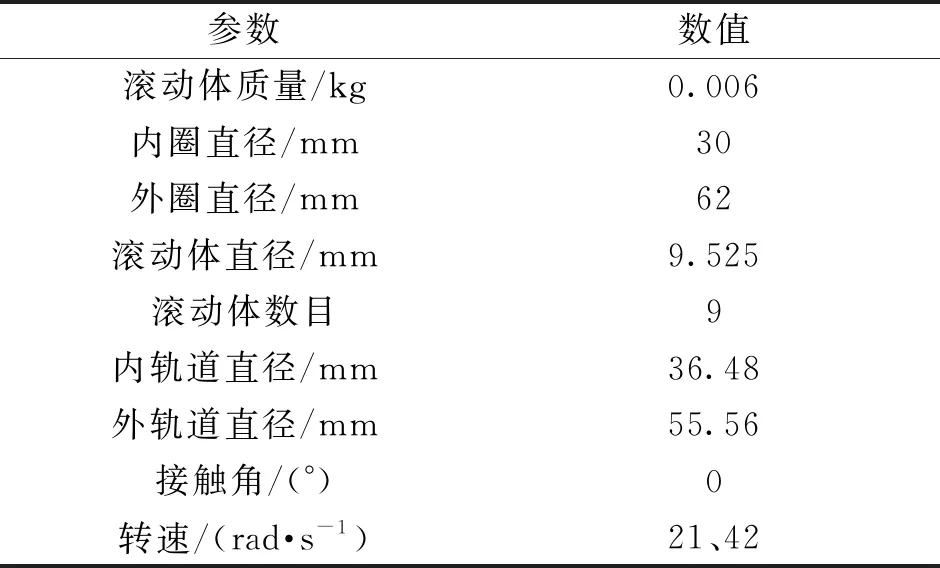
表1 6206轴承的几何尺寸和物理属性

图4 故障轴承试验台

采用电火花在轴承上加工矩形凹槽作为故障缺陷，故障尺寸6 mm×0.5 mm×0.5 mm如图5所示，其中一个轴承只在外圈上加工矩形故障，另一个轴承的内圈和外圈上分别加工矩形故障。

图5 6206轴承局部缺陷图片

图6展示了轴承振动数据采集的示意图，如图6所示，数据采集系统是由加速度传感器(LC0101)、NI采集系统(采集单元：9 234)、数据传输线和计算机组成。数据采集的过程：传感器用于采集轴承和齿轮箱的振动信号，所采集的振动信号通过数据线和NI采集系统传输到计算机中，并在计算机中做进一步的处理与分析。通过改变电机转速(200 r/min、400 r/min)和更换不同故障的轴承，分别采集了不同转速、不同故障类型的试验轴承的振动数据。由于试验台上的噪声较大，因此采用了带阻滤波器，滤除了部分噪声，以提高试验结果的可读性。

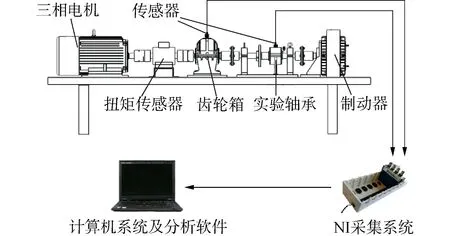
图6 数据采集示意

1)外圈故障。

图7(a)和(b)分别是仿真和实测数据在转速为21 rad/s时的时域图，图中都存在着周期性振动。图7(c)和(d)分别是仿真和实测数据的频域图，仿真数据的转动频率为3.36 Hz与实测信号的转动频率3.16 Hz非常接近，并且仿真数据中出现了外圈的故障频率11.9 Hz及其倍频，约等于实测数据的外圈故障频率11.4 Hz及其倍频。

图7 外圈故障轴承(21 rad/s)

由图4可知，试验轴承位于减速齿轮箱和磁力制动器之间，因此试验轴承处的转动速度略低于理论上的转动速度，进而引起了试验轴承的转动频率、外圈故障频率和内圈故障频率都略低于理论计算结果；在试验过程中，不可避免地会受到外界环境(如温度变化、润滑、磨损等)的影响，这些因素不仅会影响试验结果的时域波形，还可能在频域图中产生比仿真结果更多的峰值；轴承的非线性动力学模型是一种理想的计算模型，一旦确定了模型中的参数，其将不受外界因素(比如温度、润滑、磨损等)的影响，因此仿真结果中的噪音非常少。

图8(a)和(b)分别是仿真和实测数据在转速为42 rad/s时的时域图，图中都存在周期性冲击振动。图8(c)和(d)分别是仿真和实测数据的频域图，图8(c)中转动频率为6.67 Hz，约等于图8(d)中的转动频率6.4 Hz，图8(c)中出现了外圈的故障频率23.78 Hz及其倍频，与图8(d)中的外圈故障频率23.03 Hz及其倍频非常相近。

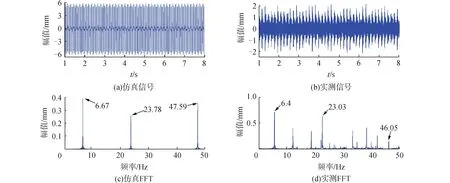
图8 外圈故障轴承(42 rad/s)

2)内外圈混合故障。

图9(a)和(b)分别是仿真和实测数据在转速为21 rad/s时的时域图，两图中都存在周期性的冲击振动。图9(c)和(d)分别是仿真和实测数据的频域图，图9(c)中的转动频率为3.34 Hz约等于图9(d)中的转动频率3.16 Hz，图9(c)中的外圈故障频率为11.44 Hz，内圈故障频率为18.1 Hz，分别与图9(d)中的外圈故障频率11.4 Hz和内圈故障频率19 Hz相近，并且图9(c)和(d)中都出现了转动频率、外圈故障频率和内圈故障频率的倍频。

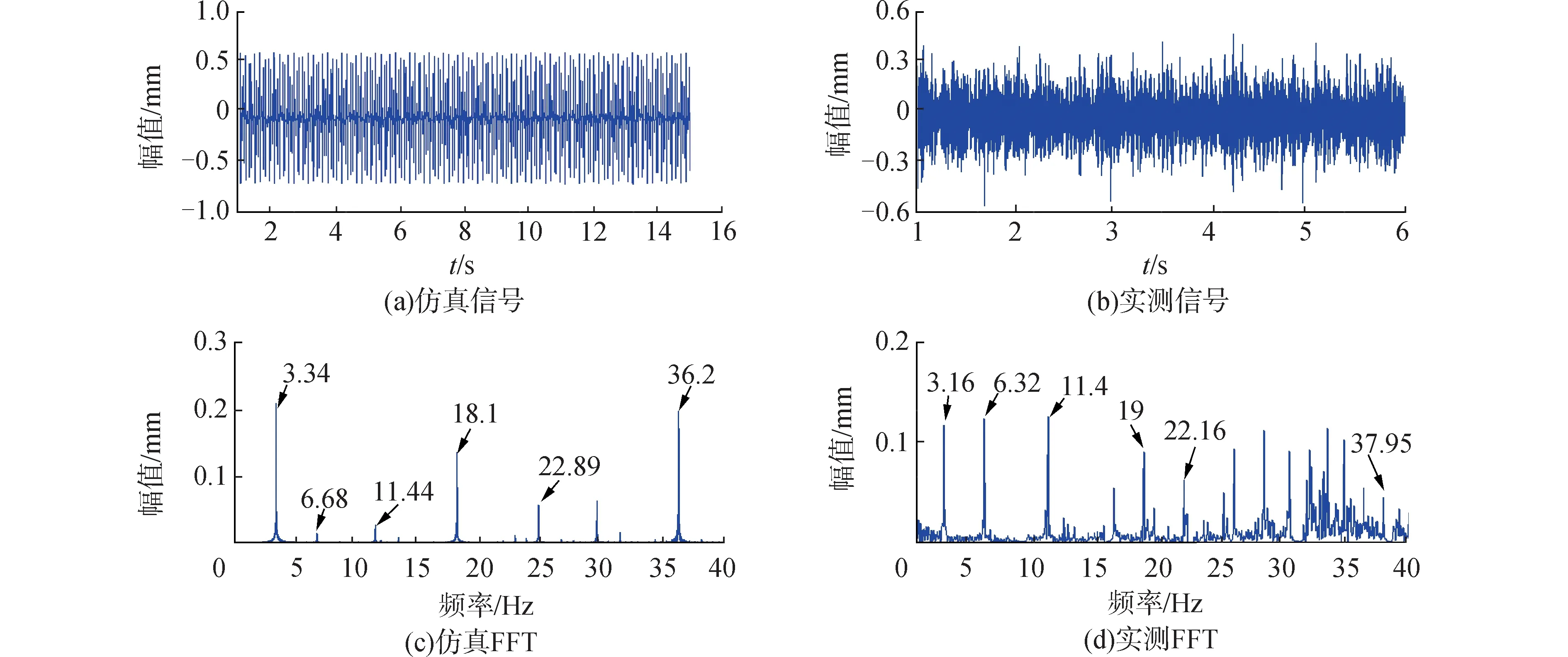
图9 混合故障轴承(21 rad/s)

图10(a)和(b)分别是仿真和实测数据在转速为42 rad/s时的时域图，仿真和实测的时域图中都存在周期性的冲击振动。图10(c)和(d)分别是仿真和实测数据的频域图，图10(c)中转动频率为6.67 Hz约等于图10(d)中的转动频率6.36 Hz；图10(c)中的外圈故障频率为22.87 Hz，内圈故障频率为36.2 Hz，分别与图10(d)中的外圈故障频率22.93 Hz和内圈故障频率35.06 Hz非常接近，并且仿真和实测数据的频率图中均出现了转动频率、外圈故障频率以及内圈故障频率的倍频。

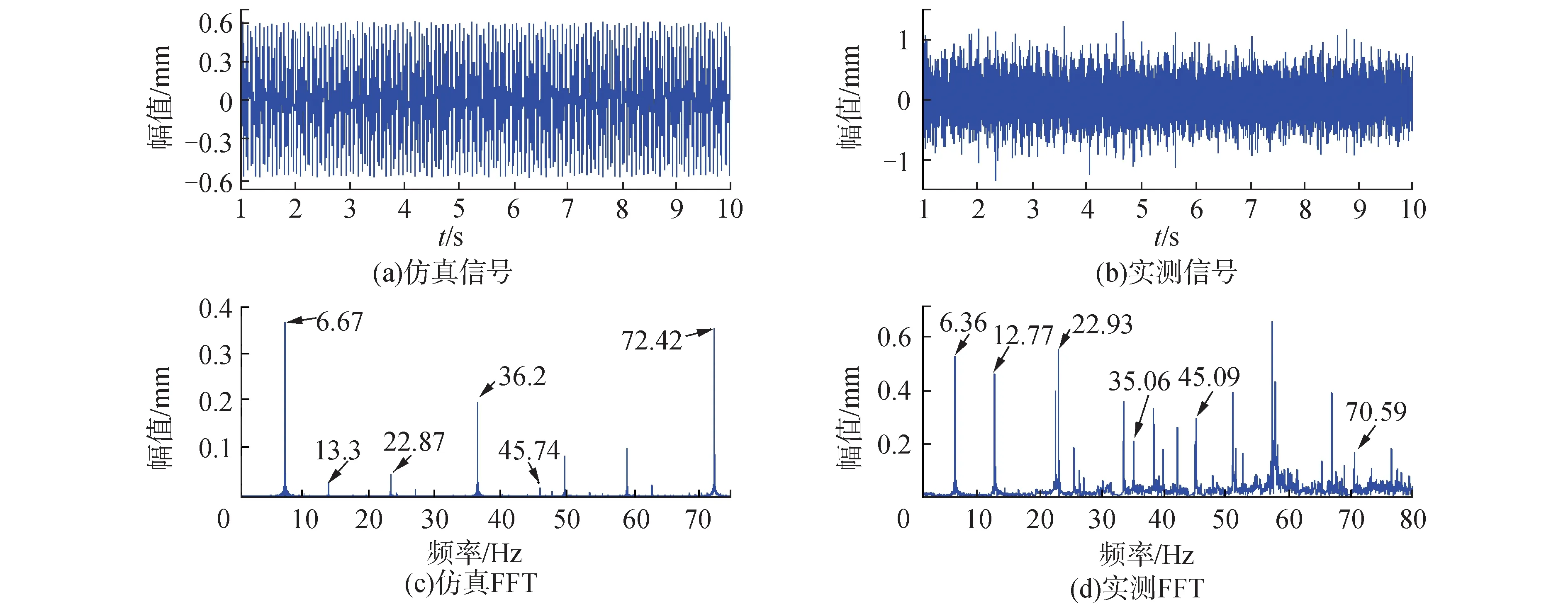
图10 混合故障轴承(42 rad/s)

5 结论

1)当滚动轴承的外圈发生故障时，振动响应的时域图中会出现周期性的冲击振动，频率图中会出现转轴的转动频率、轴承外圈的特征频率及其倍频；

2)当滚动轴承的内外圈发生混合故障时，振动响应的时域图中会出现周期性的冲击振动，频率图中会出现转轴的转动频率及倍频、轴承外圈的特征频率及倍频和轴承内圈的特征频率及倍频。