混合配筋偏心受压构件正截面承载力计算理论和方法
张望喜,胡彬彬,易伟建1,
(1.工程结构损伤诊断湖南省重点实验室(湖南大学),湖南长沙 410082;2.湖南大学土木工程学院,湖南长沙 410082)
钢筋混凝土结构耐久性问题引起了人们的广泛关注,钢筋锈蚀是造成钢筋混凝土结构过早失效的主要原因之一,各国每年花费大量的人力与物力用于结构加固或替换[1].目前,减少钢筋锈蚀的方法主要有:增大混凝土的保护层厚度、提高混凝土的密实性、在钢筋表面涂抹环氧树脂等[2-3],虽然这些方法延缓了钢筋的锈蚀,但难以从根本上解决混凝土结构耐久性问题.为此,必须找到一种耐腐蚀并且可以代替钢筋作用的材料.纤维增强复合材料(FRP)筋是一种抗拉强度高、密度小、耐腐蚀性好的筋材,并且和混凝土有良好的共同工作性能[4],因此可以替代混凝土构件中的普通钢筋[5],从而改善或解决由钢筋锈蚀导致的混凝土结构耐久性问题.
目前,FRP 筋已在实际工程中广泛应用,包括大跨度桥梁梁板、临时基坑支护、水工构筑物、特殊的军用建筑、医疗核磁共振设备等[6-7].由于FRP 筋具有较低的弹性模量、线弹性的本构关系[8-9],配置FRP 筋的混凝土构件可能会发生脆性破坏,在正常使用状态下也可能会产生过大的裂缝宽度和挠度.在矩形截面的混凝土构件中,边角区钢筋由于双向侵蚀和应力共同作用,导致较早出现锈蚀,因此可以将FRP 筋布置在截面易发生腐蚀的边角区域,将普通钢筋布置在截面内部,这样不仅改善了钢筋混凝土结构耐久性问题,也解决了FRP 筋混凝土结构脆性破坏的问题[10-11].
很多学者进行了FRP 筋混凝土受压构件的试验研究,并发现FRP 筋与混凝土具有良好的共同工作性能[12-14],我国规范[15-16]也涉及到了FRP 筋受压构件的设计计算.当钢筋和FRP 筋混合配筋用在混凝土偏压构件中时,由于FRP 筋和钢筋物理性能以及力学性能不同,已有规范的承载力计算公式不再适用于钢筋和FRP 筋混合配置的混凝土偏压构件承载力计算.本文基于若干假定,以玻璃纤维增强复合材料(GFRP)筋为例,推导出钢筋和GFRP 筋混合配筋混凝土偏压构件的承载力计算公式,为实际工程计算提供安全可靠的依据.
1 混合配筋混凝土偏压构件破坏特征
1.1 破坏类型
根据试验现象和结果[4,17-24],偏心荷载作用下混合配筋混凝土柱的破坏类型可归结为三种:屈服-受拉破坏、屈服-受压破坏和受压破坏.
1.1.1 屈服-受拉破坏
当轴向力N的偏心距较大,且纵向钢筋的配筋率不高时,在N作用下截面呈现出部分受压、部分受拉的特点.随着荷载的增加,混凝土受拉侧很快出现横向裂缝,由于纵筋配筋率不高,受拉纵筋的应力增长较快,钢筋先屈服,钢筋塑性伸长导致裂缝向受压区急剧扩展,而后GFRP 筋被拉断.在这种破坏形式下,受拉钢筋先屈服,实现了刚度的转折,表现出一定的延性破坏的特征.
1.1.2 屈服-受压破坏
这类破坏形式,和屈服-受拉破坏相似.不同之处在于,钢筋屈服后,GFRP 筋在受压区混凝土达到极限压应变之前没有被拉断.此时该破坏模式具有明显的预兆,横向裂缝快速扩展,变形显著增大,具有塑性破坏的特点.
1.1.3 受压破坏
当轴向力N的偏心距较小,或偏心距较大且纵向钢筋的配筋率很高时,在N作用下截面可能呈现出部分受压、部分受拉或全截面受压的状态.远离轴力一侧的钢筋未发生屈服,GFRP 筋未破坏,靠近轴力一侧的混凝土达到极限压应变.这类破坏发生时,没有明显的预兆,具有脆性破坏的特点,在设计时应该避免此类破坏的发生.
1.2 界限破坏
从上述破坏类型可以看出,屈服-受拉破坏与屈服-受压破坏的区别就在于GFRP 筋是否被拉断,屈服-受压破坏与受压破坏的区别就在于钢筋是否屈服.若钢筋屈服且构件以GFRP 筋被拉断而破坏,则是屈服-受拉破坏;若钢筋屈服且构件以混凝土被压碎而破坏,则是屈服-受压破坏;若钢筋未屈服且构件以混凝土被压碎而破坏,则是受压破坏.
图1 所示为混合配筋混凝土偏心受压构件的截面应变,图中εs为远离轴力一侧的纵筋拉应变,εfu为GFRP 筋极限拉应变,εy为钢筋屈服时对应的拉应变,εcu为混凝土的极限压应变.当εs>εfu时,钢筋屈服,GFRP 筋被拉断,截面为屈服-受拉破坏(如图1中的ab);当εs=εfu时,GFRP筋被拉断的同时,受压区边缘混凝土达到极限压应变,为屈服-受拉破坏与屈服-受压破坏的界限(如图1中的ac);当εy<εs<εfu时,钢筋屈服,GFRP筋未被拉断,混凝土被压碎,截面为屈服-受压破坏(如图1中的ad);当εy=εs<εfu时,为屈服-受压破坏与受压破坏的界限(如图1 中的ae);当εs<εy时,钢筋未屈服,截面为受压破坏(如图1 中的af);当到达g点时,进入全截面受压状态.由此可以计算出屈服-受拉破坏与屈服-受压破坏的相对界限受压区高度ξb1以及屈服-受压破坏与受压破坏的相对界限受压区高度ξb2.当ξ≤ξb1时,为屈服-受拉破坏;当ξb1<ξ≤ξb2时,为屈服-受压破坏;当ξ>ξb2时,为受压破坏.
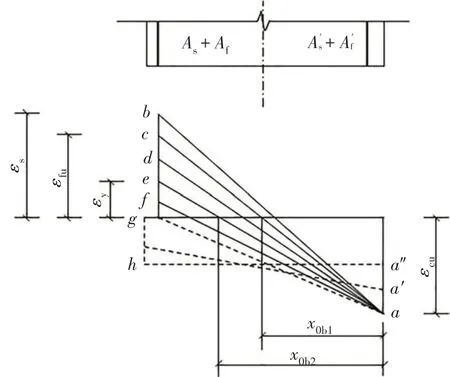
图1 偏心受压构件的截面应变Fig.1 Section strain of eccentric compression member
式中:xb1、xb2以及x0b1、x0b2分别为按等效矩形应力图形以及平截面假定计算的受压区高度;h0为截面有效高度;β1为和等效矩形应力图形有关的参数;ffu为GFRP 筋极限抗拉强度;fy为钢筋屈服强度;Ef和Es分别为GFRP筋和钢筋的受拉弹性模量.
2 偏压构件正截面承载力计算
2.1 基本假定
本文的公式推导基于以下假定:1)截面应变符合平截面假定[25];2)不考虑受拉区混凝土的抗拉强度;3)钢筋和GFRP 筋与混凝土有良好的黏结作用,在截面同一位置处,钢筋与GFRP 筋应变相同;4)混凝土受压的应力-应变曲线,按GB 50010—2010[26]中的规定采用,见图2(a);5)钢筋和GFRP 筋受拉的应力-应变曲线见图2(b)和(c);6)纵筋的应力为纵筋的应变乘以相应的弹性模量,但不超过其抗拉强度与抗压强度.
GFRP筋线弹性的本构关系,导致其发生脆性破坏,为了使GFRP 筋在使用时具有一定的安全储备度,取其抗拉强度设计值[16,26-27]为:

式中:ffy、ffk分别为GFRP 筋的抗拉强度设计值、标准值;γf为GFRP筋的材料分项系数,取1.25;γe为GFRP 筋的环境影响系数,室内环境取1.25,一般室外环境取1.4,海洋环境、侵蚀性环境取1.6(强碱环境取2.0);CE为GFRP 筋环境折减系数,非侵蚀环境取0.8,侵蚀环境取0.7.
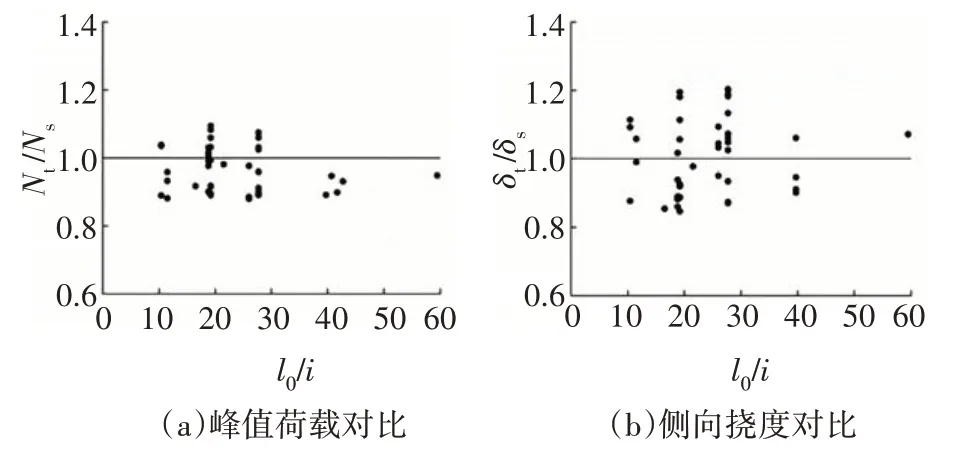
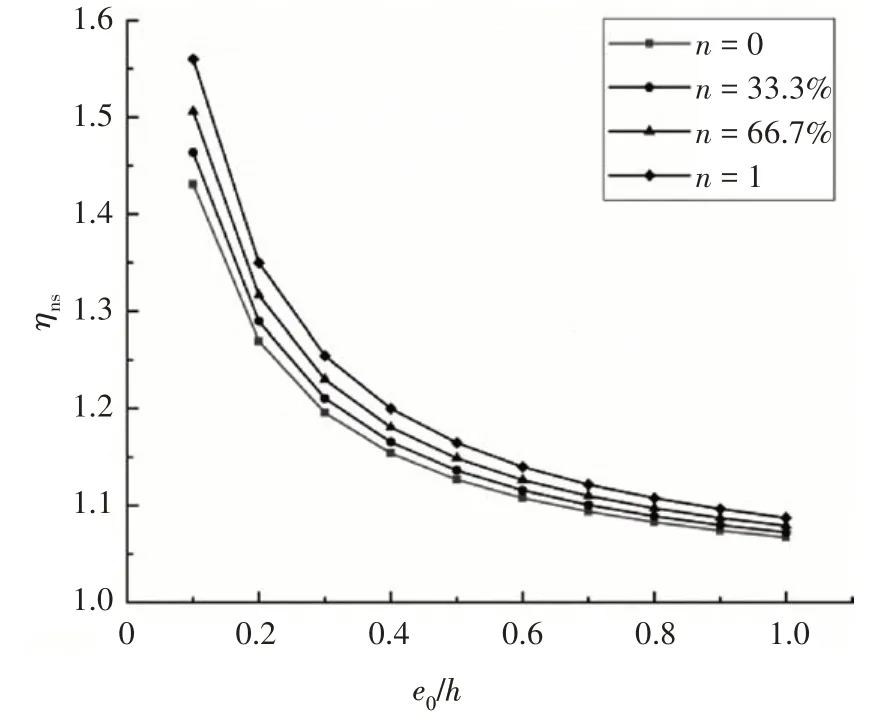
在混合配筋混凝土柱中,当GFRP筋达到设计应力时,由平截面假定可知,钢筋应力σs=Esffy/Ef,若钢筋未屈服,则σs=Esffy/Ef 关于混合配筋的配置形式,部分学者更加倾向于在单层配筋中用GFRP筋代替部分钢筋,但为了更好地解决由钢筋锈蚀导致的混凝土耐久性问题,也有对双层混合配筋混凝土柱的研究,在外侧配置GFRP 筋,在内侧配置钢筋.此时,钢筋与GFRP 筋的有效高度h0=h-c-ds-d-4s/5,其中h为截面高度,c为保护层厚度,ds为箍筋直径,d为外侧GFRP 筋直径,s为两排配筋之间的距离,通过这种方法计算的有效高度,具有更高的安全系数,下面证明这种计算方法的可行性.图3 为双层混合配筋示意图,h01、h02为钢筋、GFRP筋合力作用点到截面受拉受压分界点的距离. 图3 双层混合配筋示意图Fig.3 Schematic diagram of double layer mixed reinforcement 钢筋和GFRP 筋分别对分界点的弯矩的和为Mh=σsAsh01+σfAfh02,钢筋和GFRP 筋合力作用点对分界点的弯矩为Mh0=(σsAs+σfAf)(4h01/5+h02/5).由平截面假定可知,εf=εsh02/h01,假设钢筋的弹性模量是GFRP筋的4 倍,一排和二排配筋面积相等,则有Mh-Mh0=(EsεsAfh02/5h01-EsεsAs/5)(h02-h01)>0,说明利用上述公式计算的有效高度是偏于安全的. 当偏心受压构件的长细比以及轴压比偏大,反弯点不在杆件高度范围内时,经P-δ效应放大后,弯矩控制截面可能会从构件端部转移到构件中部.因此,在截面设计时应考虑P-δ效应的不利影响. 2.3.1 长细比限值 我国规范GB 50010—2010[26]和美国规范ACI 318—19[28]中对需要考虑钢筋混凝土柱P-δ效应的情况进行了规定,即单曲率对称弯曲的钢筋混凝土柱的长细比大于22.但由于GFRP 筋的弹性模量低于钢筋,文献[29]建议单曲率对称弯曲的FRP 筋混凝土柱长细比限值取17.为了充分考虑附加挠度对构件产生的影响,钢筋和GFRP筋混合配筋混凝土柱长细比限值也取17.当混合配筋混凝土柱长细比满足式(4)时,不需要考虑P-δ效应[30]. 式中:l0为构件计算长度;i为回转半径;M1、M2分别为已经考虑侧向挠度的偏心受压构件两端截面按弹性分析确定的对同一主轴的组合弯矩设计值,绝对值较小的杆端弯矩为M1,绝对值较大的杆端弯矩为M2,当构件单曲率弯曲时,M1和M2均取正值,否则取负值. 2.3.2 二阶弯矩增大系数 由于GFRP筋和钢筋力学性能的差异,很难通过理论推导得出正确的弯矩增大系数[31].因此,本文将基于ABAQUS 有限元软件进行参数分析拟合出混合配筋混凝土柱二阶弯矩增大系数. 为验证利用ABAQUS 有限元软件进行数值分析的正确性,建立了46 个模型[4,18-24],将由模拟得出的偏压柱峰值荷载和峰值荷载下对应的侧向挠度和试验结果进行对比,结果见图4.Nt/Ns表示试验峰值荷载和模拟峰值荷载的比值,δt/δs表示试验侧向挠度和模拟侧向挠度的比值,Nt/Ns的平均值为0.955,标准差为0.004,δt/δs的平均值为0.986,标准差为0.029.由此可见,ABAQUS 可以较好地模拟混合配筋混凝土柱的承载力和侧向挠度. 图4 模拟结果和试验结果对比Fig.4 Comparison of simulation and experimental results 混凝土柱二阶弯矩增大系数可通过式(5)计算. 式中:e0为轴压对截面重心的偏心距;af为混凝土柱破坏时的侧向挠度. 在验证ABAQUS 可以较准确地模拟混合配筋混凝土柱偏压性能的基础上,对混合配筋混凝土柱进行了参数分析,具体的参数见表1. 表1 参数取值Tab.1 Parameter values 将侧向挠度af代入式(5)中,即得到数值分析下的二阶弯矩增大系数,将所有参数下计算的结果进行回归分析,得到混合配筋混凝土柱二阶弯矩增大系数的计算公式: 式中:ζc为截面曲率修正系数;ea为附加偏心距. 将钢筋混凝土柱与混合配筋混凝土柱的二阶弯矩增大系数绘于图5.由图5可知,随着GFRP筋配筋面积占比的增加,二阶效应增大,这是因为GFRP 筋的弹性模量比钢筋的弹性模量小,在相同条件下,将产生更大的侧向挠度;当e0/h增大时,弯矩增大系数减小,说明二阶效应在偏心距较小时更加显著. 图5 二阶弯矩增大系数对比Fig.5 Comparison of moment amplification factors 2.4.1 屈服-受拉破坏 如图6(a)所示,发生屈服-受拉破坏时,受拉一侧的钢筋屈服,GFRP 筋达到极限抗拉强度,根据轴力和力矩平衡可得: 式中:e为轴向压力作用点至纵向受拉筋材合力点的距离;x为混凝土受压区高度;As′ 和Af′分别为受压钢筋和受压GFRP 筋的截面面积;As和Af分别为受拉钢筋和受拉GFRP 筋的截面面积;σf′为破坏时受压GFRP 筋的应力;as′为受压纵筋合力点至截面较近边缘的距离. 由于GFRP筋拉断时,混凝土受压侧还没有达到极限压应变,α1在屈服-受拉破坏下取为0.7.为了充分利用钢筋的抗压强度,保证钢筋达到抗压强度设计值,应该满足x≥2a′s的要求,否则,受压钢筋的应力应该通过平截面假定进行推导,如式(9);GFRP筋的弹性模量较小,达不到其抗压强度设计值,受压一侧GFRP筋的应力利用式(10)进行计算. 式中:as′为受压钢筋的应力;Es′和Ef′分别为钢筋和GFRP筋的受压弹性模量. 2.4.2 屈服-受压破坏 如图6(b)所示,发生屈服-受压破坏时,受拉一侧的钢筋屈服,受压区混凝土被压碎,这时 式中:σf为破坏时受拉GFRP筋的应力. 受拉一侧GFRP筋应力通过平截面假定可知: 2.4.3 受压破坏 如图6(c)所示,发生受压破坏时,距离轴力较远一侧的钢筋未屈服,受压区混凝土被压碎,这时 图6 矩形截面承载力计算示意图Fig.6 Bearing capacity calculation diagram of rectangular section 式中:σs为破坏时受拉钢筋的应力. 远离轴力一侧的钢筋应力σs的表达式为: 2.4.4 临界偏心距 当发生屈服-受拉破坏与屈服-受压破坏的界限破坏时,其轴向力平衡条件和对截面几何中心轴取力矩的平衡条件为: 定义e0b/h0=Mb/Nbh0为“相对临界偏心距”,则有: 同理,也可以得到屈服-受压破坏与受压破坏的临界偏心距. 2.4.5 公式说明与讨论 1)当只配置GFRP 筋时,可以递归到GFRP 筋混凝土偏压构件正截面承载力计算公式. 当ξ≤ξb1时,发生受拉破坏,即受拉侧GFRP 筋被拉断,截面承载力按下式计算: 式中:α1、取值同2.4.1节. 当ξ>ξb1时,发生受压破坏,即受压区混凝土被压碎,远侧GFRP 筋未达到极限抗拉强度.截面承载力按下式计算: 2)在进行混合配筋偏压构件屈服-受拉破坏以及GFRP 筋混凝土偏压构件受拉破坏正截面承载力计算时,GFRP 筋使用的是极限抗拉强度,但GFRP筋应力-应变关系呈线性,没有明显的屈服点,因此为了增加构件的安全储备,建议在进行截面设计时,使用GFRP 筋抗拉强度设计值,计算公式和上述相似,不再赘述. 根据轴力和弯矩平衡方程,可以得到轴力和弯矩之间的相关关系,现以实例说明.混凝土柱的截面尺寸b×h为340 mm×340 mm,混凝土保护层厚度c=840 MPa,混凝土柱采用对称配筋,单侧配筋形式为:柱Ⅰ选用7ϕ12,柱Ⅱ选用柱Ⅲ选用表示钢筋.设,将柱Ⅰ~柱Ⅳ的相关曲线绘于图7. 图7 偏心受压构件的-相关曲线图Fig.7 -correlation curve of eccentric compression member 选取已有文献中的试验试件,根据试件不同的破坏特征代入不同的方程组进行求解,将理论承载力值与试验承载力值进行对比,详见表2.结果表明,理论公式计算值与试验实测值相差不大(试验值与计算值之比Nu,t/Nu,e的均值为0.99,标准差为0.053),说明计算公式具有较好的准确性,可以用来指导工程设计计算. 表2 试验值与理论值对比Tab.2 Comparisons between experimental values and theoretical values 1)钢筋和GFRP 筋混合配筋偏心受压构件有屈服-受拉破坏、屈服-受压破坏以及受压破坏三种破坏模式. 2)当混合配筋混凝土偏压构件的长细比大于17时,可依据本文推导的考虑GFRP筋配筋面积占比的二阶弯矩增大系数考虑侧向挠度对构件承载力的不利影响. 3)基于若干假定推导出的矩形截面偏心受压构件承载力计算公式具有良好的准确性和适用性,可为混合配筋混凝土构件在实际工程中的应用和推广提供一定的理论指导和设计借鉴.2.2 混合配筋配置形式

2.3 P-δ二阶效应



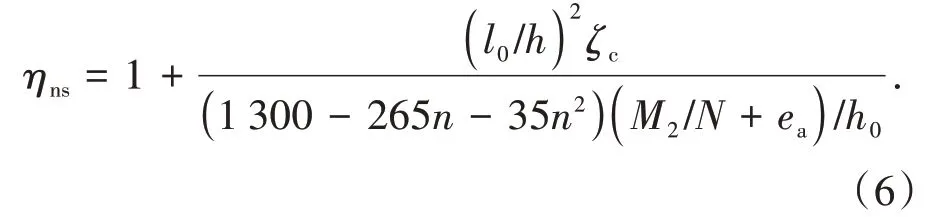
2.4 矩形截面偏压构件计算方法
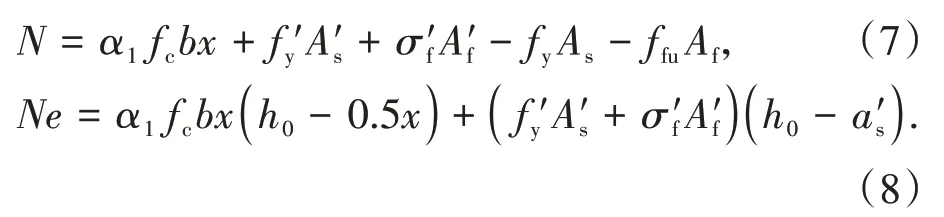
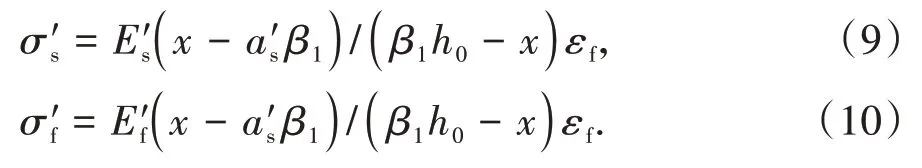

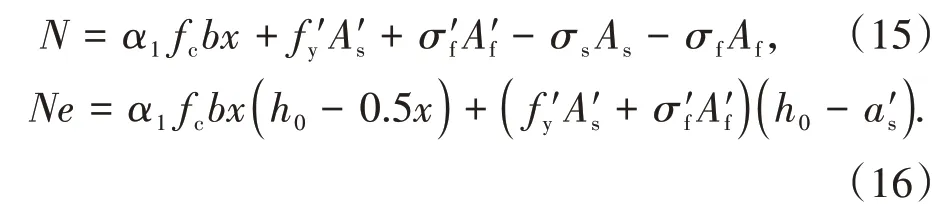

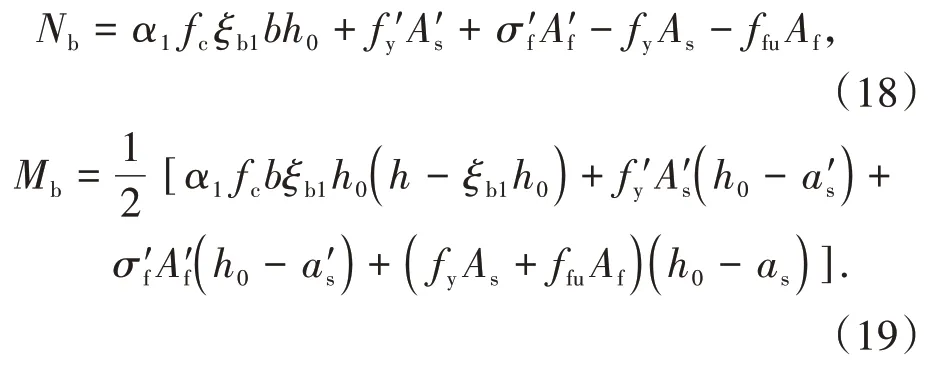
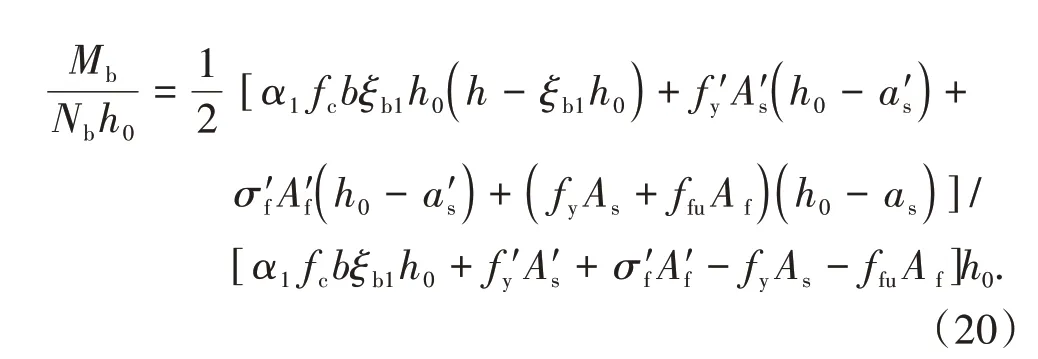
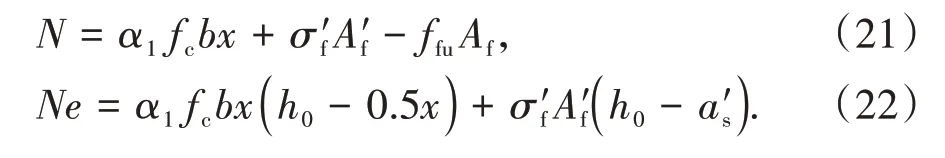


3 公式准确性对比验证

4 结论

