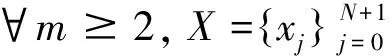B样条拟插值算子的逼近
郭红焱
(云南民族大学 预科教育学院,云南 昆明 650031)
0 引 言
二十世纪以来,函数逼近论得到了高速发展,它不仅能够研究多项式函数、线性算子等的最佳逼近,还渗透到泛函分析、调和分析、代数、小波分析,成为计算数学、应用数学、优化理论、计算机辅助设计等学科的理论基础和方法依据,特别是应用于计算机领域数据的模拟和分析.我们知道,插值和拟插值是经常用到的两种方法,然而在大规模的数据面前,一般是采用拟插值的方法,它可以直接构造出一个整体逼近的形式,因此构造具有良好性质的拟插值已很有必要[1-6].
在已知节点的情形下,拟插值的标准形式是

(1)局部逼近性,即(Snh)(x)在x点的值仅依赖于h(x)及其若干阶导数在x点的领域上的值;
(2)逼近阶的最佳性,即(Snh)(x)逼近光滑函数h(x)可达到最好可能的样条函数的逼近阶;
(3)对l次多项式的再生性,这里k (Snp)(x)=P(x). 性质(3)是保证性质(2)的关键,我们的构造也就从抓住性质(3)和性质(1)入手. 下列性质1到性质3可在参考文献[3]中找到,性质4和性质5可在参考文献[4,6]中找到. 性质1 递推关系:当m≥2时,m阶B样条定义为: 性质2 正定与紧支性: 性质4 对∀τ∈R, 证明我们已经知道对∀m≥2均有 成立,又在性质4中,取τ=0,即可得 我们先给出k泛函与光滑模的定义如下: 我们知道k泛函与光滑模具有等价等质,即 c1wr(f,t)∞≤Kr,∞(f,t)≤c2wr(f,t)∞,c1 其中Zj(h)是h(xj),h(xj+1),…,h(xj+m)的组合. 设(Snh)(x)是C[a,b]中的正线性算子系列,如果对于fi(x)=xi,i=0, 1, 2,则该算子在[a,b]上一致收敛于fi(x),则对于每个函数f(x)∈C[a,b],(Snf)(x)在[a,b]上一致收敛于f(x).为了得到较高的逼近阶,我们对 B样条拟插值算子进行加权逼近[9-10],其中Jacobi权为: 满足‖Snh-h‖∞≤c3tr-1‖g(r-1)‖∞. 证明由h(x)满足的性质,先取在x0=0处,由麦克劳林公式可得: 又记 因为对∀x∈R都成立,故在其它点处由Taylor公式同样可得. 此时不妨设|x| 而又因为(Snh)(x)具有局部多项式的再生,所以有: (Snpx0)(x)=Px0(x). 又因为‖wkSn(h)‖∞≤M‖wkh‖∞,‖wk(Sn(h)-h)‖∞≤Mn-1‖wkh″‖∞(其中M表示与h,n,x无关的正常数),从而得到: ‖wk(Snh-h)‖∞ =‖wk(Snh-Px0(x)+Px0(x)-h)‖∞ =‖wk(Snh-Px0(x)+Snpx0(x)-h)‖∞ ≤‖wk(Snh-Px0(x))‖∞+‖wk(Shpx0(x)-h)‖∞ =(1+‖Sn‖)|h(x)-Px0(x)|≤c3hr-1‖f(r-1)‖≤MKwk(h,n-1). 在这里需要证上面的‖Sn‖有界. 证明因为 ‖(Snh)(x)‖≤c‖h‖∞,则‖Sn‖≤c.又其中Zj(h)是h(xj),h(xj+1),…,h(xj+m)的组合,即 ∑Zj(h)=c1h(xj)+c2h(xj+1)+…+cm+1h(xj+m) ≤|c1h(xj)|+|c2h(xj+1)|+…+|cm+1h(xj+m)|≤(k+1)cm‖h(xj+m-1)‖≤(k+1)cm‖h‖∞. 这里取(k+1)cm=c. 研究本节需用到如下知识. (1)对每个f∈Lp[a,b],(1≤p≤∞,本文假设L∞=c) (2)(Minkowski不等式)设p≥1,f∈Lp[a,b],g∈Lq[a,b] ,那么f+g∈Lp[a,b],并且下列不等式成立 ‖f+g‖p≤‖f‖p+‖g‖p. ‖f-Sh(f)‖p[xi,xi+1]≤c4[‖f-g‖p[xi,xi+1]+hm‖g(m)‖p[xi,xi+1]],∀g∈cm[xi,xi+1] 证明由定理1可以得到: |f(x)-Sh(f)(x)|≤c5hr-1w(f(r-1),h)Ii, ‖f-Sh(f)‖p[xi,xi+1]=‖f-g+g-Sh(f)‖p[xi,xi+1]≤‖f-g‖p[xi,xi+1]+‖g-Sh(f)‖p[xi,xi+1]. 又因为 ‖g-Sh(f)‖p[xi,xi+1] =‖g-Px0(x)+Px0(x)-Sn(f)‖p[xi,xi+1] =‖g-Px0(x)+Snpx0(x)-Sn(f)‖p[xi,xi+1] ≤‖g-Px0(x)‖+‖Snpx0(x)-Sn(f)‖p[xi,xi+1] ≤(1+‖Sn‖)|g(x)-Px0(x)|p[xi,xi+1] ≤c6hm‖g(m)‖p[xi,xi+1], 故 ‖f-Sh(f)‖p[xi,xi+1] ≤‖f-g‖p[xi,xi+1]+‖g-Sh(f)‖p[xi,xi+1] ≤‖f-g‖p[xi,xi+1]+c6hm‖g(m)‖p[xi,xi+1] ≤c4[‖f-g‖p[xi,xi+1]+hm‖g(m)‖p[xi,xi+1]] ,∀g∈cm[xi,xi+1] . 定理证毕.1 C空间下B样条拟插值算子的逼近
1.1 B样条的定义及性质

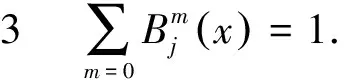
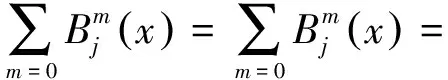




1.2 预备知识
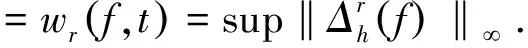
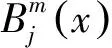
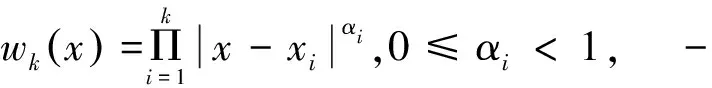

2 Lp空间下B样条拟插值算子的逼近