高强超高延性混凝土梁弯剪性能理论分析与数值模拟

蔡自伟，邓博予，张 智，陆洲导，李凌志，俞可权

（同济大学土木工程学院，上海 200092）

超高延性混凝土（engineered cementitious composite，ECC）是根据微观力学原理由短切高性能纤维增强水泥基材料制备而成［1］。ECC具有较高的拉伸强度、较好的拉应变硬化能力和多裂缝开裂行为，极限拉应变可达普通混凝土的几百倍，微细裂缝宽度小于150 μm。基于优异的力学和耐久性能，ECC 在结构抗震［2］、结构修复和加固［3］、抗爆［4］和抗火［5］等工程中得到广泛应用。

目前常规强度ECC主要由聚乙烯醇（PVA）纤维制备而成，PVA-ECC稳态拉伸裂缝宽度通常小于100 μm，极限拉应变通常介于3%～5%之间［6-7］。然而，由于PVA属亲水性纤维，PVA-ECC制备时需限制纤维与基体间的黏结力以免纤维过早拉断，而且配比对原材料敏感度高，因此所得PVA-ECC抗压强度不超过60 MPa［6-7］。PVA-ECC的弹性模量通常为其对应强度混凝土的60%～70%，作为结构构件材料应用时，难以满足正常使用极限状态下构件的挠度限值要求。为进一步提升ECC的拉压强度、弹性模量以及拉伸延性，推动ECC在结构构件中的广泛应用，研究人员尝试采用超高分子量聚乙烯（ultra-high molecular weight polyethylene,UHMWPE）纤维制备高强ECC［8-9］。UHMWPE纤维具有高弹性模量、高抗拉强度和天然憎水性，可制备圆柱体抗压强度为40～120 MPa、抗拉强度高达16 MPa、极限拉应变不小于8%、弹性模量达到40 GPa 的 高 强ECC（high-strength engineered cementitious composite，HS-ECC）［10-11］，HS-ECC的结构应用也因此备受关注［12-13］。

由于混凝土自身脆性以及抗拉强度和拉应变低，普通钢筋混凝土梁通常带裂缝工作，较大的裂缝宽度易引发钢筋腐蚀，达到极限荷载时受压区混凝土压溃。已有研究人员将ECC 应用于配筋受弯梁中，并探讨了受弯承载力计算模型［14］、弯曲挠度计算方法［15］、试件的受力响应［16］以及配筋率和ECC替代率对ECC-混凝土复合梁受弯性能的影响［17］。然而，前述研究中ECC的弹性模量不超过20 GPa，导致受弯构件在正常使用极限状态下的挠度较大。HSECC 的弹性模量高达40 GPa，可有效控制构件变形。此外，HS-ECC兼具高拉伸强度与高延性，具有部分甚至全部取代纵向钢筋的能力，其承载力与变形的理论模型也需进一步推导。

对于ECC梁的抗剪性能，研究人员提出了配筋ECC梁受剪承载力的计算方法，探讨了不同配筋率下无腹筋ECC梁以及不同配箍率、纤维掺量、剪跨比下配箍ECC梁的受剪性能变化规律［18-19］，建立了基于拉压杆模型［20］或修正压力场［21］的配筋ECC梁抗剪承载力理论模型，并与规范中的计算方法进行了对比。鉴于HS-ECC优异的拉压强度、拉伸和压缩变形能力，将HS-ECC用于受弯构件的剪跨区以抵抗剪切作用，可降低配箍率，同时改善脆性的剪切破坏模式。目前关于配筋HS-ECC梁受剪性能的研究尚未开展，HS-ECC亦有望进一步提升构件的抗剪性能。

目前，由于成本较高、施工复杂、设计理论不完善等问题，HS-ECC结构应用仍受到限制，已有研究人员尝试通过降低纤维掺量或将ECC 用于构件关键位置来解决这些问题［17］。基于前期试验结果［12］，采用理论分析和有限元方法开展了配筋HS-ECC梁的弯剪性能研究，分析了混凝土类型、配筋率和是否配置箍筋三因素对配筋HS-ECC梁受弯和受剪性能的影响；得到了试件的破坏模式和荷载-位移曲线，并利用平截面假定和材料本构关系推导了受弯承载力以及弯矩-曲率和荷载-应变关系；计算了试件的受剪承载力。基于Abaqus 软件建立了配筋HSECC梁的有限元模型，模拟了配筋HS-ECC梁的受弯和受剪破坏过程。

1 试验概况

试件的几何尺寸和配筋分别如图1和表1所示。共制作14 根梁，无配筋HS-ECC 梁（NU）2 根，有配筋钢筋混凝土梁（RC）6根，有配筋HS-ECC梁（RU）6 根，其中只配纵筋的钢筋混凝土梁与HS-ECC 梁（NS）各3 根。梁的截面尺寸为100 mm×100 mm，总长度为500 mm。研究因素为混凝土类型、纵筋配筋率和是否配置箍筋。纵筋配筋率分别为0.69%、1.86%和2.94%。纵筋保护层厚度为15 mm。

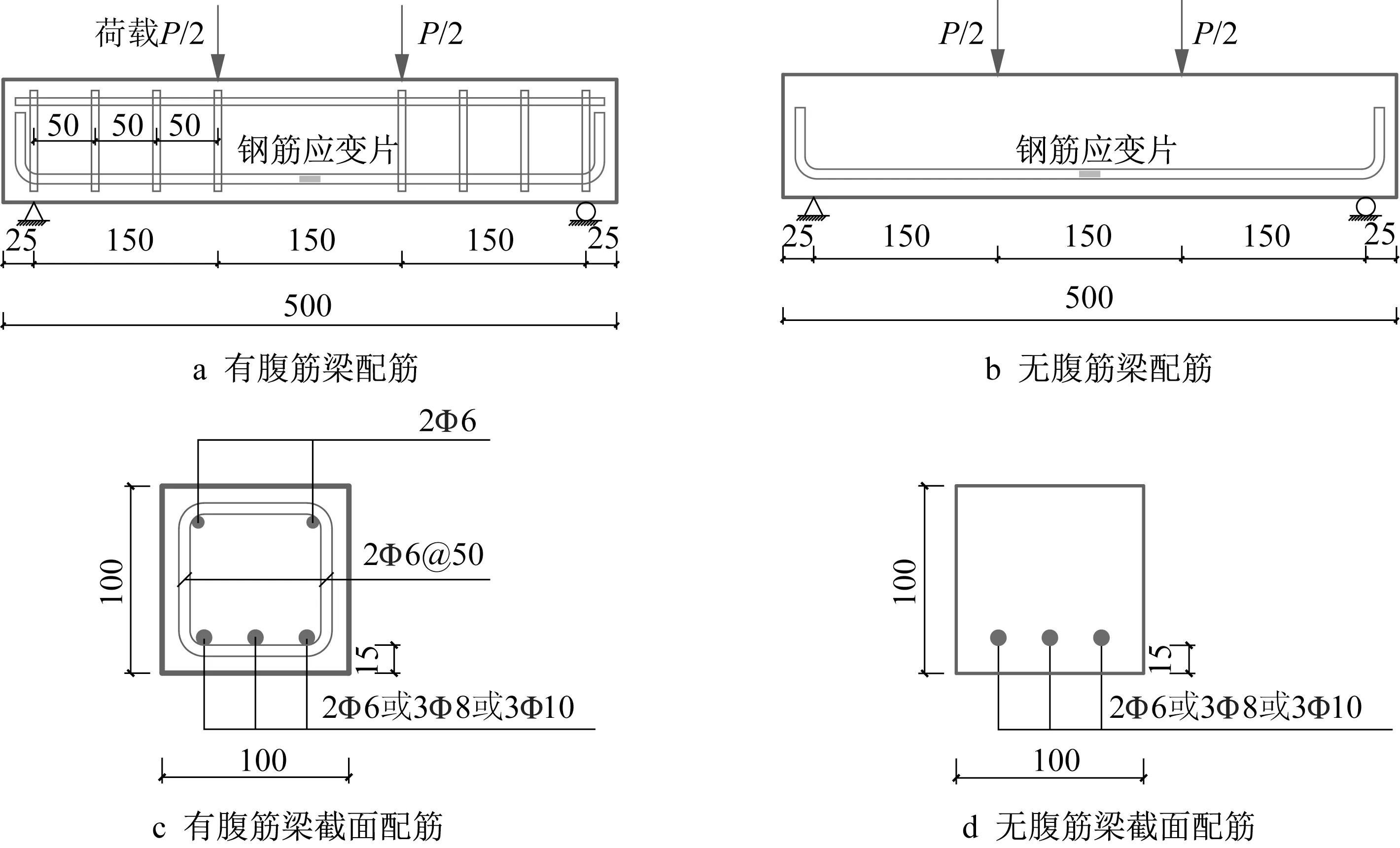
图1 试件的几何尺寸和配筋（单位：mm）Fig.1 Geometric parameters and reinforcement of specimens (unit：mm)

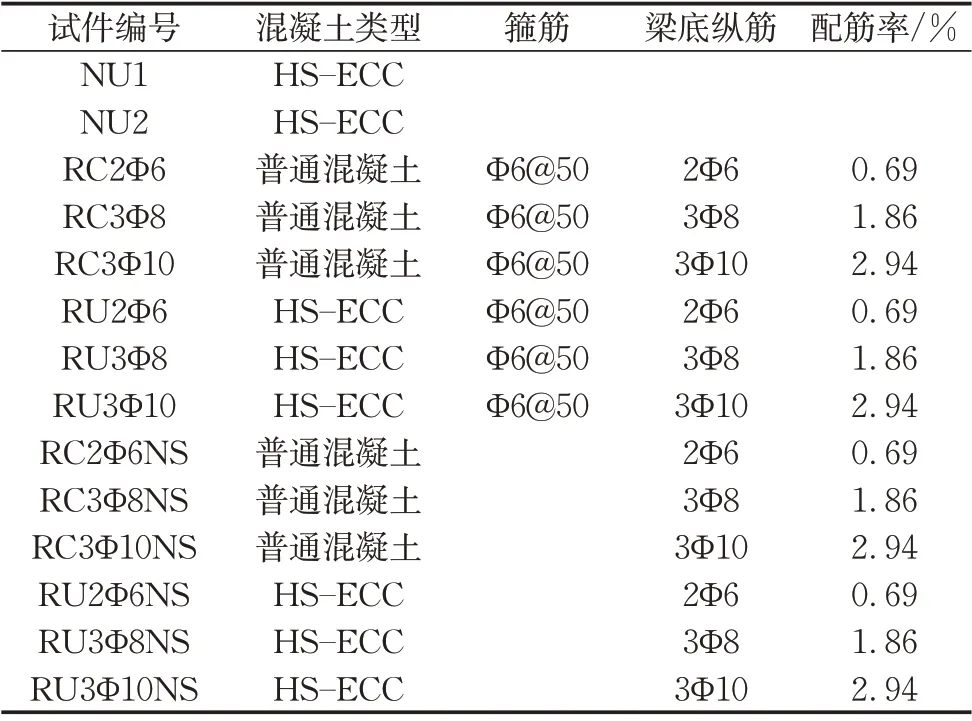
表1 试件的几何尺寸和配筋Tab.1 Geometric parameters and reinforcement of specimens

试件加载装置和测点布置如图2所示。采用电液伺服试验机加载，试验机量程为500 kN。加载方式为四点弯曲加载，试件净跨度为450 mm，纯弯段和剪跨区均为150 mm。采用位移控制方式，加载速率为1 mm·min−1。共采用5 个位移计，分别布置于支座、跨中和加载点，测量试件的竖向位移，同时采 用数字图像相关法［5］测量试件的位移变化。

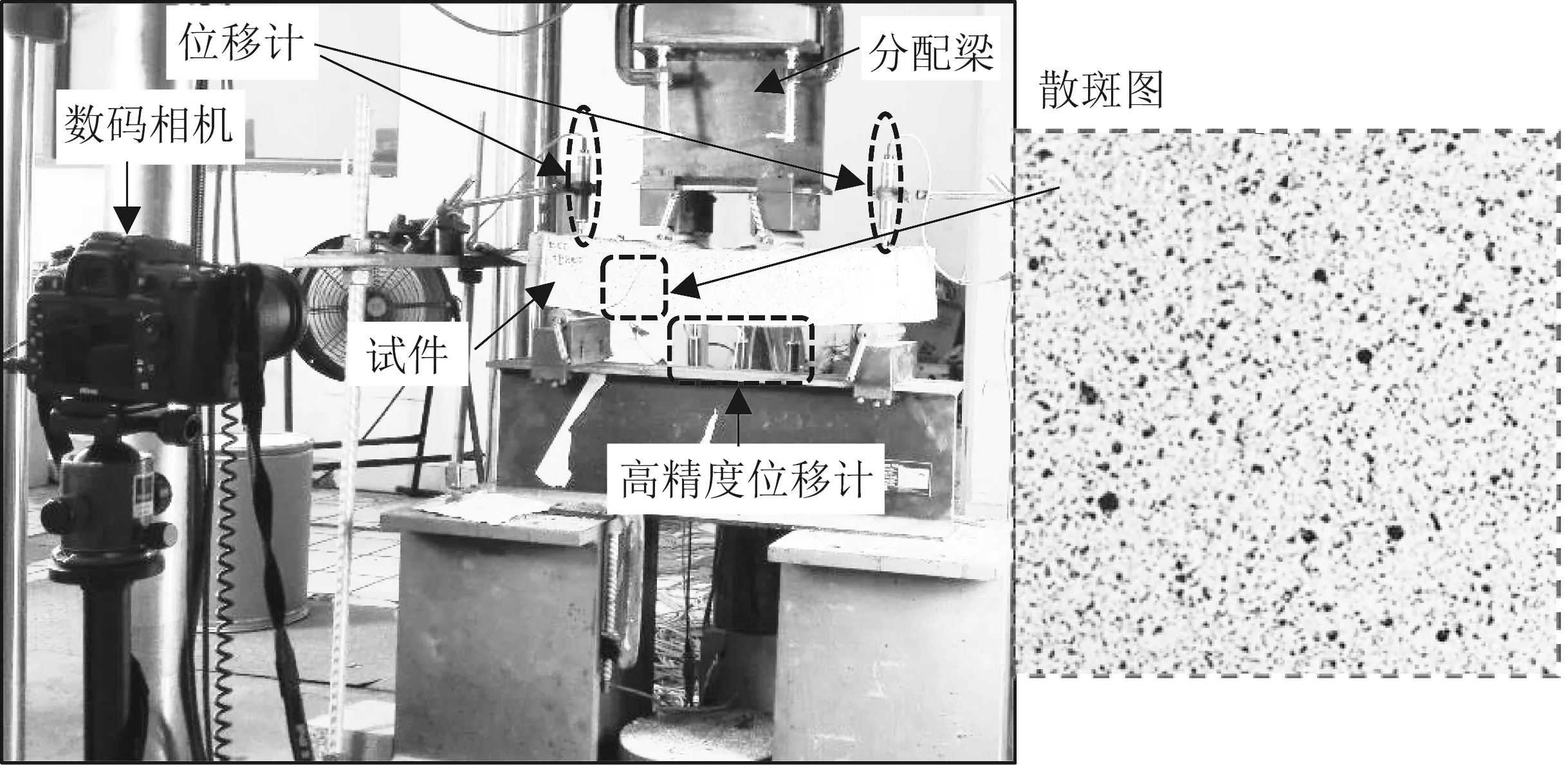
图2 加载装置、位移测点布置和数字图像相关法Fig.2 Loading setup,instrumentation layout and digital image correlation method

2 试验结果与讨论

2.1 破坏模式

如图3a所示，试件NU1和NU2为受弯破坏，试件破坏时纯弯段受拉区产生大量微细弯曲裂缝。对于配置箍筋和纵筋的梁，如图3b、c所示，钢筋混凝土梁和HS-ECC梁均表现为受弯破坏。试件的破坏模式类似，仅展示典型试件RC3Φ8和RU3Φ8。配筋HS-ECC梁发挥了HS-ECC优异的拉伸与压缩应变能力，梁跨内底部弯曲裂缝发展充分，而顶部纯弯段HS-ECC仅有轻微压溃现象，配筋HS-ECC梁表现出优异的弯曲延性。详细试验结果参考文献［12］。对于只配置纵筋的梁，试件RC2Φ6NS和RU2Φ6NS亦为受弯破坏，其余4根梁均发生受剪破坏。如图3e所示，在主斜裂缝形成前试件RU3Φ8NS有明显的多裂缝分散行为，表现出优异的变形能力，从而将脆性剪切破坏转换为延性剪切破坏。

图3 典型破坏模式［12］Fig.3 Typical failure modes［12］

2.2 荷载-跨中位移曲线

试件的荷载-跨中挠度曲线如图4 所示。如图4a 所示，对于受弯构件，随着配筋率增大，钢筋混凝土梁与HS-ECC梁的承载力和刚度均逐渐增大。由于跨中截面顶部HS-ECC相比普通混凝土具有更高的压缩变形能力，因此HS-ECC 梁的延性并未显著降低［12］。对比相同配筋率的钢筋混凝土梁和HSECC 梁，HS-ECC 梁表现出更优异的承载力与延性性能。HS-ECC 的高拉伸强度提升了构件的承载力，而高延性与多裂缝开展能力则有利于与钢筋之间的变形协调，提升构件延性。无箍筋HS-ECC 梁的受弯性能略小于配筋率为1.86%的钢筋混凝土梁，证明了HS-ECC 具备部分取代纵筋的能力。如图4b所示，RC2Φ6NS和RU2Φ6NS均表现为受弯破坏，这是因为此配筋率下梁的抗弯承载力仍小于抗剪承载力。当配筋率增大到1.86%和2.94%时，梁的受弯承载力大于受剪承载力，钢筋混凝土梁和HS-ECC 梁均发生受剪破坏。随着配筋率的增大，试件的承载力和刚度逐渐增大，但延性逐渐降低。需要指出的是，受剪破坏的HS-ECC 梁仍具有与受弯钢筋混凝土梁相当的延性［12］。

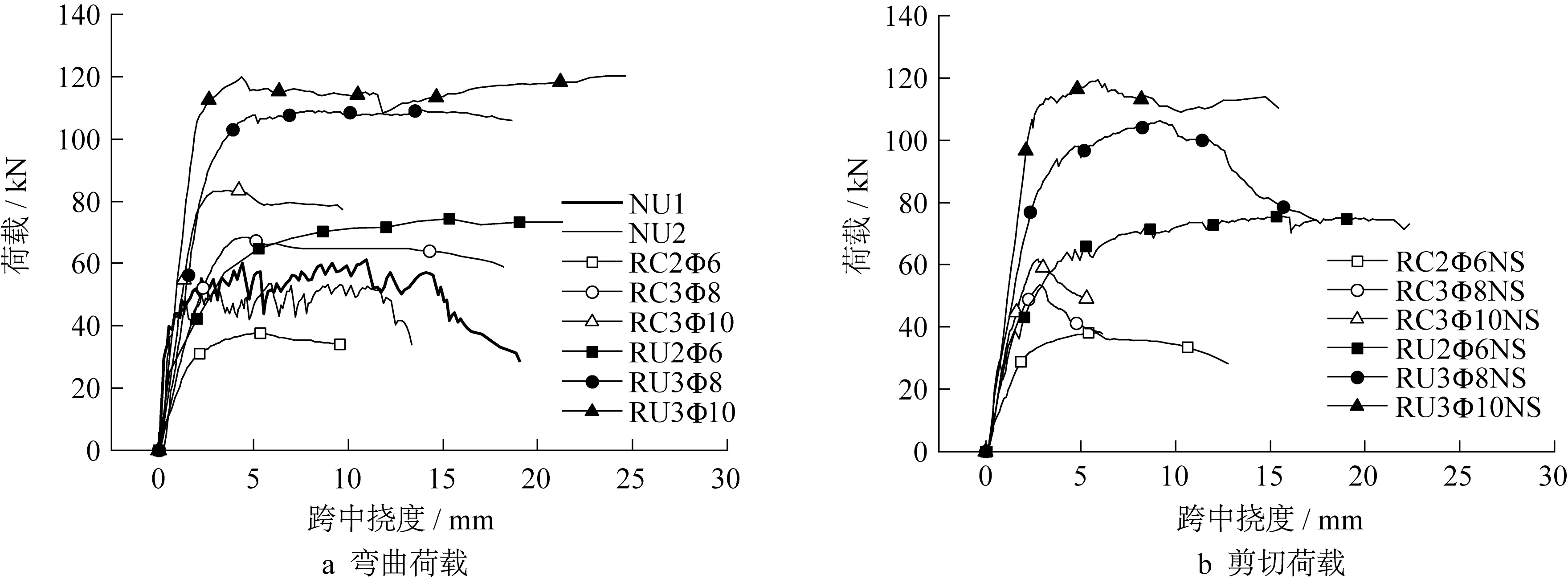
图4 荷载-跨中挠度曲线Fig.4 Load-midspan deflection curves

3 受弯承载力计算模型

根据平截面假定、钢筋和HS-ECC 的材料本构关系，推导未配筋和配筋HS-ECC 梁受弯截面的开裂弯矩、屈服弯矩和极限弯矩公式，再计算试件的开裂荷载、屈服荷载和极限荷载。

3.1 基本假定

作如下基本假定：

（1）HS-ECC 梁符合平截面假定。以试件RU3Φ8 为例，借助数字图像相关法，最终获得不同荷载和跨中挠度下纯弯段上沿高度方向的HS-ECC水平应变分布，如图5 和图6 所示。可见，试件RU3Φ8 纯弯段HS-ECC 的水平应变基本符合平截面假定。

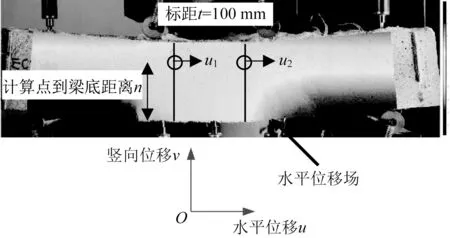
图5 HS-ECC梁水平位移示意图Fig.5 Schematic diagram of horizontal displacement of HS-ECC beams

图6 试件RU3Φ8的平截面假定验证Fig.6 Plain-section assumption verification for RU3Φ8

（2）纵筋与HS-ECC共同变形。HS-ECC具有较高的基体强度和大掺量纤维，能够保证与钢筋之间的荷载传递。因此，假定钢筋和HS-ECC之间完全黏结。

（3）在整个加载过程中，考虑拉区HS-ECC的贡献。如图6 所示，极限荷载时配筋HS-ECC 梁RU3Φ8 底部的最大拉应变仅达到2%，小于HSECC 材料本身的极限拉应变，表明这一假定是合理的。

3.2 材料本构关系

3.2.1 HS-ECC的理论应力-应变曲线

采用简化的二折线模型表征HS-ECC 拉压本构，图7a和式（1）为HS-ECC的理论拉伸应力-应变曲线，图7b和式（2）为HS-ECC的理论压缩应力-应变曲线。

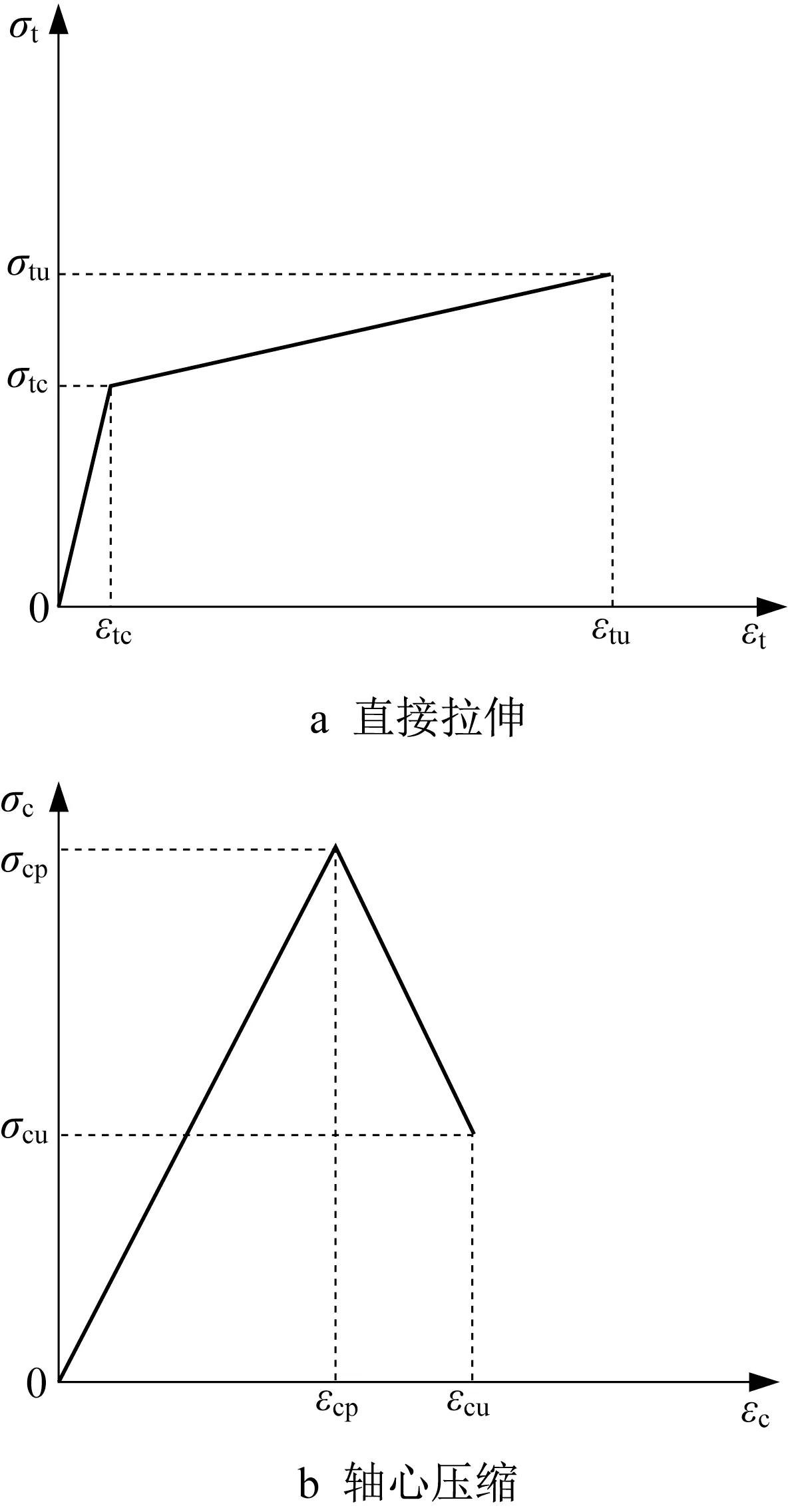
图7 HS-ECC的理论应力-应变曲线Fig.7 Theoretical stress-strain curves of HS-ECC

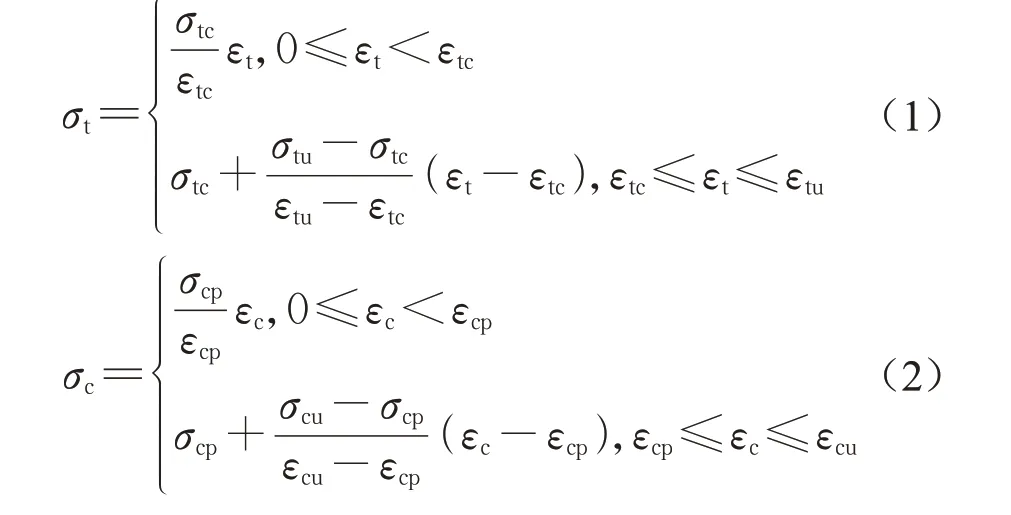
式中：σtc和εtc分别为开裂强度和开裂应变；σtu和εtu分别为极限抗拉强度和极限拉应变；σcp和εcp分别为峰值抗压强度和压应变；σcu和εcu分别为极限压应力和压应变。

HS-ECC拉压本构参数如表2所示。表2中，极限拉伸强度考虑了试件尺寸效应和配筋影响折减［22-23］。未配筋试件仅考虑尺寸效应，折减系数为0.9；配筋试件同时考虑尺寸效应和配筋影响折减，折减系数为0.7。对于受压性能，采用100 mm×100 mm×300 mm 棱柱体的实测受压试验数据。需指出的是，实测的受压应力-应变曲线体现的是轴心受压性能，而跨中纯弯段受压区HS-ECC 承受的是约束偏心压力，两者的本构关系存在差异，主要表现为偏压状态下峰值应力后HS-ECC的应力下降较为缓慢，在大应变下仍然保持较高的压应力。

表2 HS-ECC的本构参数Tab.2 Constitutive parameters of HS-ECC

3.2.2 钢筋的理论应力-应变曲线

为简化计算，对钢筋采用理想弹塑性应力-应变曲线。各试件理论模型中纵筋的几何和力学参数如表3所示。

表3 各试件理论模型中纵筋的几何和力学参数Tab.3 Geometric and mechanical parameters of longitudinal steel bars in the theoretical model of each specimen

3.3 弯矩作用下跨中截面沿高度方向的应力-应变分布

加载过程中应力-应变分布可分为以下4种情况：

（1）弹性阶段，从开始加载到HS-ECC 开裂（见图8a）。

（2）屈服阶段，从HS-ECC 开裂到梁底纵筋屈服。此时有2种情况：梁底纵筋屈服时，HS-ECC受压边缘应力尚未达到峰值压应力，如图8b 所示；梁底纵筋屈服时，HS-ECC 受压边缘应力介于峰值压应力和极限压应力之间，如图8c所示。

（3）破坏阶段1，从梁底纵筋屈服到受压区顶面HS-ECC受压达到峰值压应力（见图8b）。

（4）破坏阶段2，从梁底纵筋屈服到受压区顶面HS-ECC受压达到极限压应力（见图8c）。

图8 中，x为截面上任意一点到梁底的距离，ε（x）、σ（x）分别为该点的应变和应力，b和h分别为试件截面宽度和高度，m为钢筋合力作用点到梁底距离，xc为中性轴到梁顶面距离，xc=h−c，c为中性轴到梁底面距离，a为开裂强度位置到梁底的距离，β1为等效矩形高度与xc之比，β1xc为等效矩形受压区高度，α1为等效矩形受压应力与峰值抗压强度σcp之比，εs和σs分别为钢筋应变和应力。为简化计算，将受压区HS-ECC的应力分布等效为矩形分布，根据受压区HS-ECC的应力分布形式可分为线性阶段和双折线阶段2种情况。

（1）情况1，受压区线性阶段，如图8a、b所示，此时0≤εc＜εcp。力平衡时，计算式如下所示：

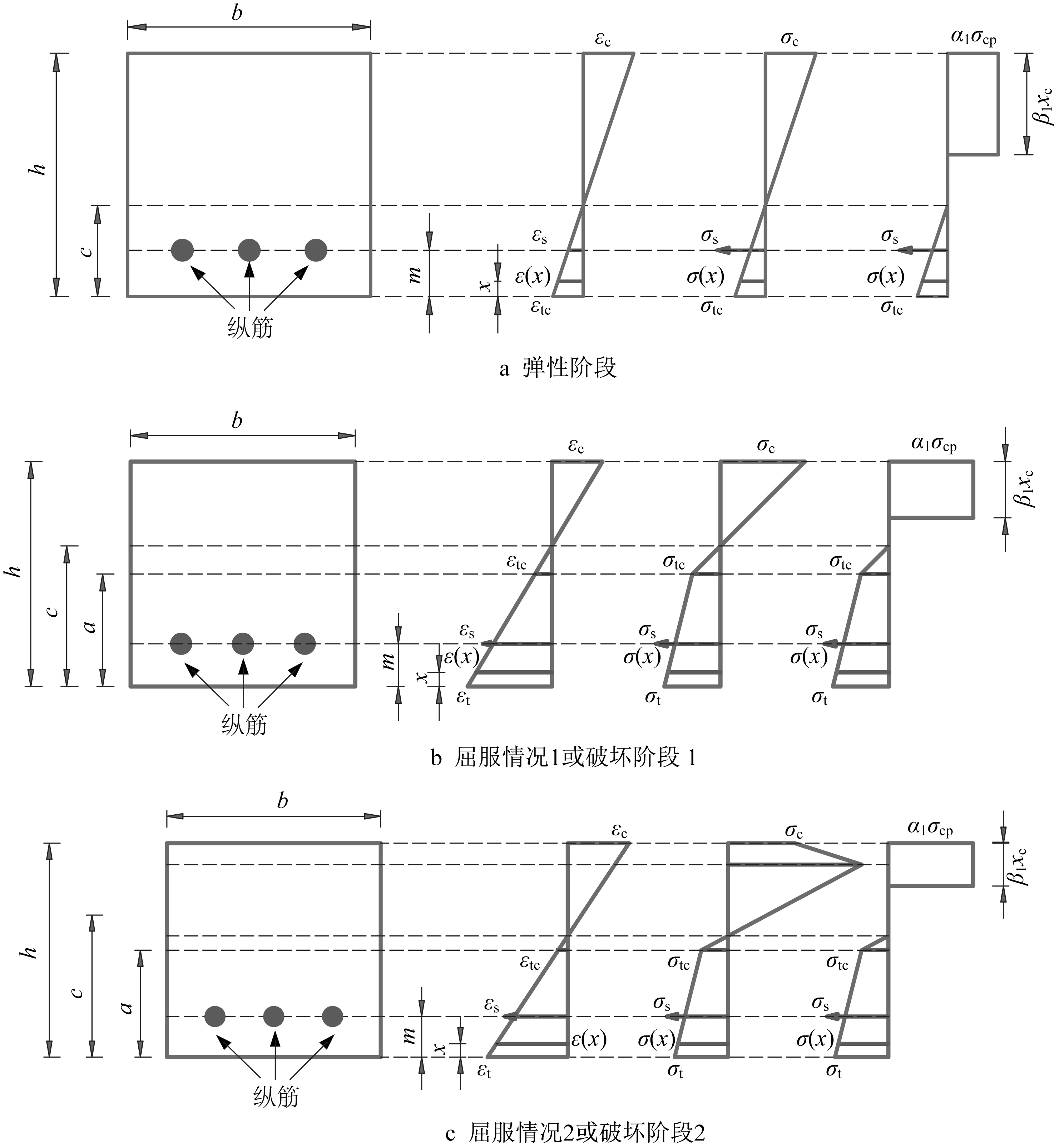
图8 跨中截面HS-ECC和钢筋沿高度方向的水平应力-应变分布Fig.8 Horizontal stress-strian distribution of HS-ECC and steel bars along the depth of midspan cross section

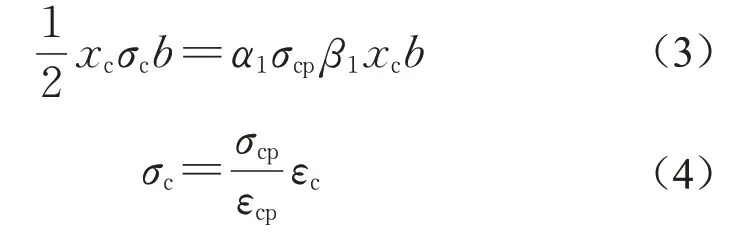
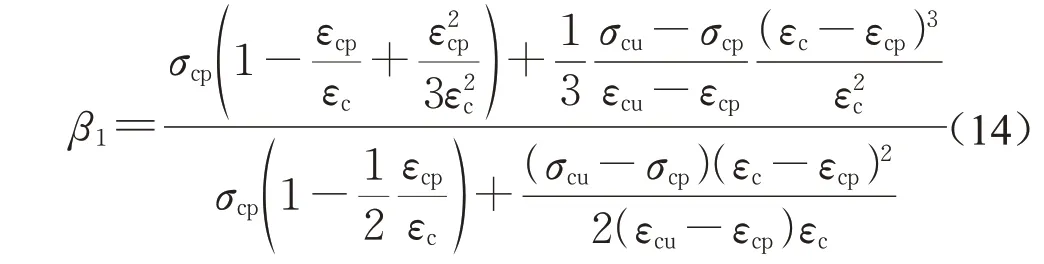
3.4 各阶段弯矩计算

随着受压区边缘HS-ECC的压应变εc从零逐渐增大到εcu，根据平截面假定，得到跨中截面沿高度方向的应变分布。根据材料的本构关系，利用应变分布计算应力分布。中性轴到梁顶面的距离xc按力平衡计算。各临界时刻的弯矩求解过程如下所示：

（1）开裂弯矩Mcr（εt=εtc）

表4对比了配筋HS-ECC梁的理论与试验抗弯承载力。随着配筋率的增加，开裂、屈服和极限弯矩均逐渐增大。配筋HS-ECC梁的最大抗弯承载力对应的受压边缘应变εc通常介于εcp和εcu之间。理论预测的初裂荷载低于试验观测到的初裂荷载，这可能是由于直接拉伸与弯曲的HS-ECC材料力学性能存在差异，直接拉伸HS-ECC 的开裂强度小于弯曲HS-ECC的开裂强度。理论预测的屈服荷载与试验观测到的屈服荷载比较接近。值得注意的是，开裂荷载和屈服荷载的判断具有一定的主观性和数据离散性，因此理论和试验获得的结果总会存在一定程度的差异。无配筋HS-ECC梁的抗弯承载力与计算值一致，配筋HS-ECC 梁的受弯承载力计算值略大于试验值，这可能是因为钢筋的配置影响了HSECC 中纤维的桥接作用。总之，该计算理论仍能比较准确地预测配筋HS-ECC梁抗弯承载力。

表4 HS-ECC梁的试验与理论抗弯承载力Tab.4 Experimental and theoretical flexural capacity of HS-ECC beams

3.5 跨中截面弯矩-曲率关系和中性轴位置发展过程

图9 为不同试件的跨中截面弯矩-曲率曲线变化过程。对比试件RU3Φ8可见，本研究建议的理论计算方法（th）较准确地预测了试件的跨中截面弯矩-曲率关系（DIC），随着配筋率的增大，峰值抗弯承载力对应的跨中截面曲率逐渐减小。图10 为中性轴高度和梁底HS-ECC 拉应变关系。随着梁底HS-ECC拉应变的增加，中性轴高度逐渐增大，说明HS-ECC 受压区域逐渐减小；峰值荷载后随着荷载的下降，中性轴高度略有下降。

图9 跨中截面弯矩-曲率曲线Fig.9 Midspan moment-curvature curves

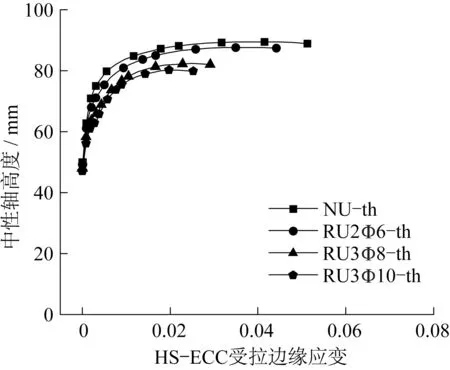
图10 中性轴高度和梁底HS-ECC拉应变关系Fig.10 Relationship between neutral axis height and tensile strain of HS-ECC at the bottom of beam

3.6 荷载-应变关系、配筋率与HS-ECC 极限拉应变需求关系以及截面曲率延性系数

荷载和HS-ECC 受拉边缘应变关系如图11 所示。对比RU3Φ8的试验和理论曲线，可知理论计算能够较好地预测HS-ECC 受拉边缘应变的发展过程。当构件跨中截面顶部混凝土达到极限压应变时，按照理论公式计算出梁底HS-ECC拉应变值，将这一应变值定义为构件对HS-ECC 的拉应变需求。若此拉应变能力刚好为HS-ECC 的极限拉应变，则意味着HS-ECC 充分发挥了自身性能，材料利用率达到理想状态。如图12 所示，随着配筋率的增大，梁底HS-ECC 拉应变需求逐渐减小。无配筋HSECC 梁的受拉边缘应变达到了5.1%（拉应变需求），配筋率2.94%梁的HS-ECC 受拉边缘应变为2.5%（拉应变需求）。配筋率的提升增强了构件受拉区的承载能力，但受压区性能未得到有效改善，构件失效由受压区HS-ECC的极限应变控制。这一试验结果亦表明，HS-ECC因其优异的拉伸延性，具备了独立承担荷载，形成无配筋构件的能力。

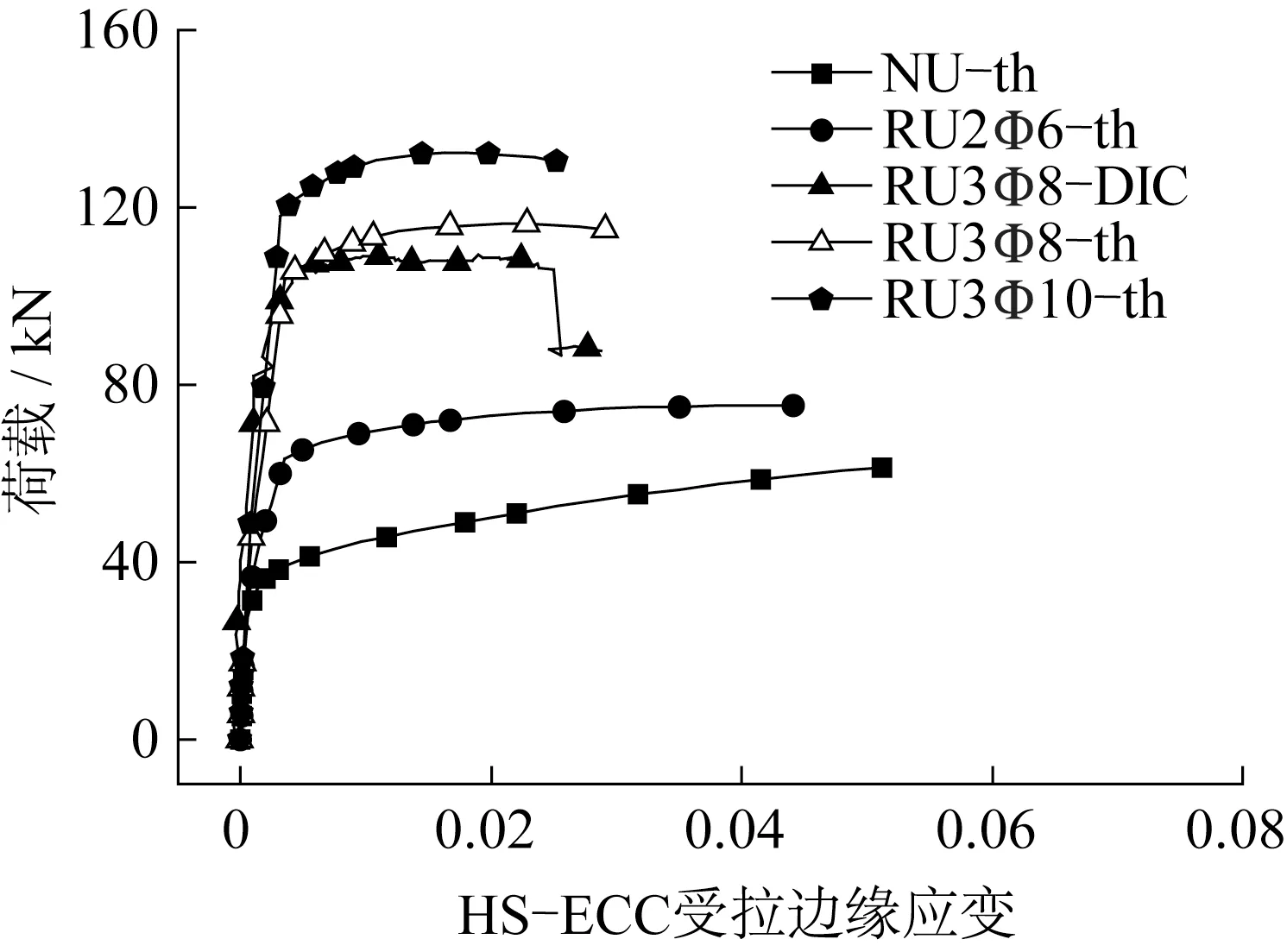
图11 荷载和HS-ECC受拉边缘应变关系Fig.11 Relationship between load and tensile strain of HS-ECC

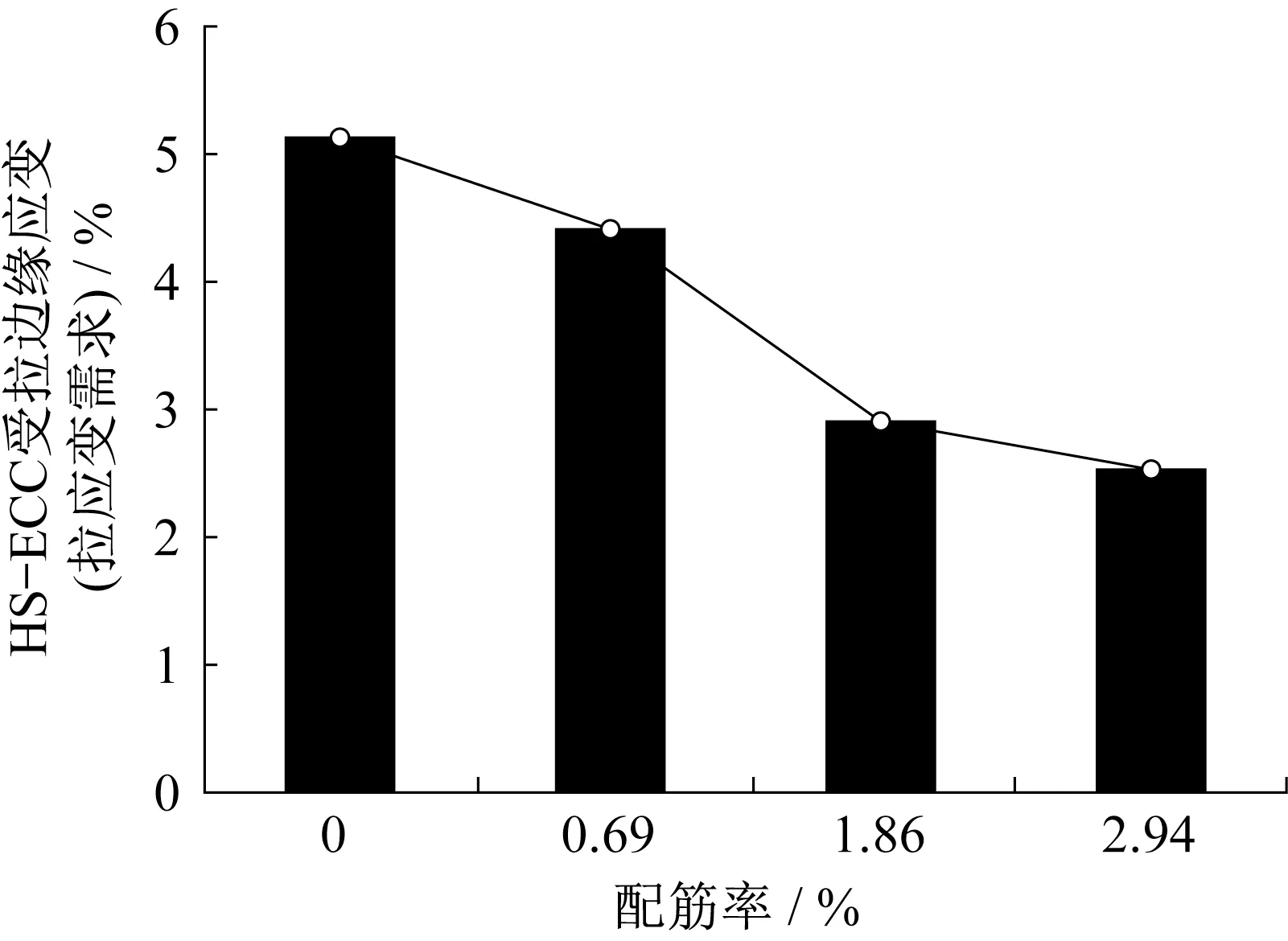
图12 配筋率与HS-ECC受拉边缘应变（拉应变需求）Fig.12 Relationship between reinforcement ratio and tensile strain of HS-ECC(tensile strain demand)

各试件荷载-纵筋应变的试验和理论曲线如图13所示。理论预测的纵筋应变发展过程与试验结果基本一致。理论分析结果表明，随着配筋率的增大，峰值荷载对应的纵筋拉应变逐渐降低。如图13 所示，RU3Φ8 和RU3Φ10 峰值荷载下应变片（exp）测得的纵筋最大应变远大于理论预测值（th）。峰值荷载根据荷载-跨中位移曲线确定。理论计算采用的钢筋本构为理想弹塑性本构，而实际试件的钢筋具有屈服后硬化段。由于HS-ECC具有极高的拉应变能力和极优异的应变硬化行为，试件的最大纵筋应变超过屈服段后可能进入硬化段，从而实现更高的极限荷载，此时试件的跨中挠度更大，纵筋应变更大。

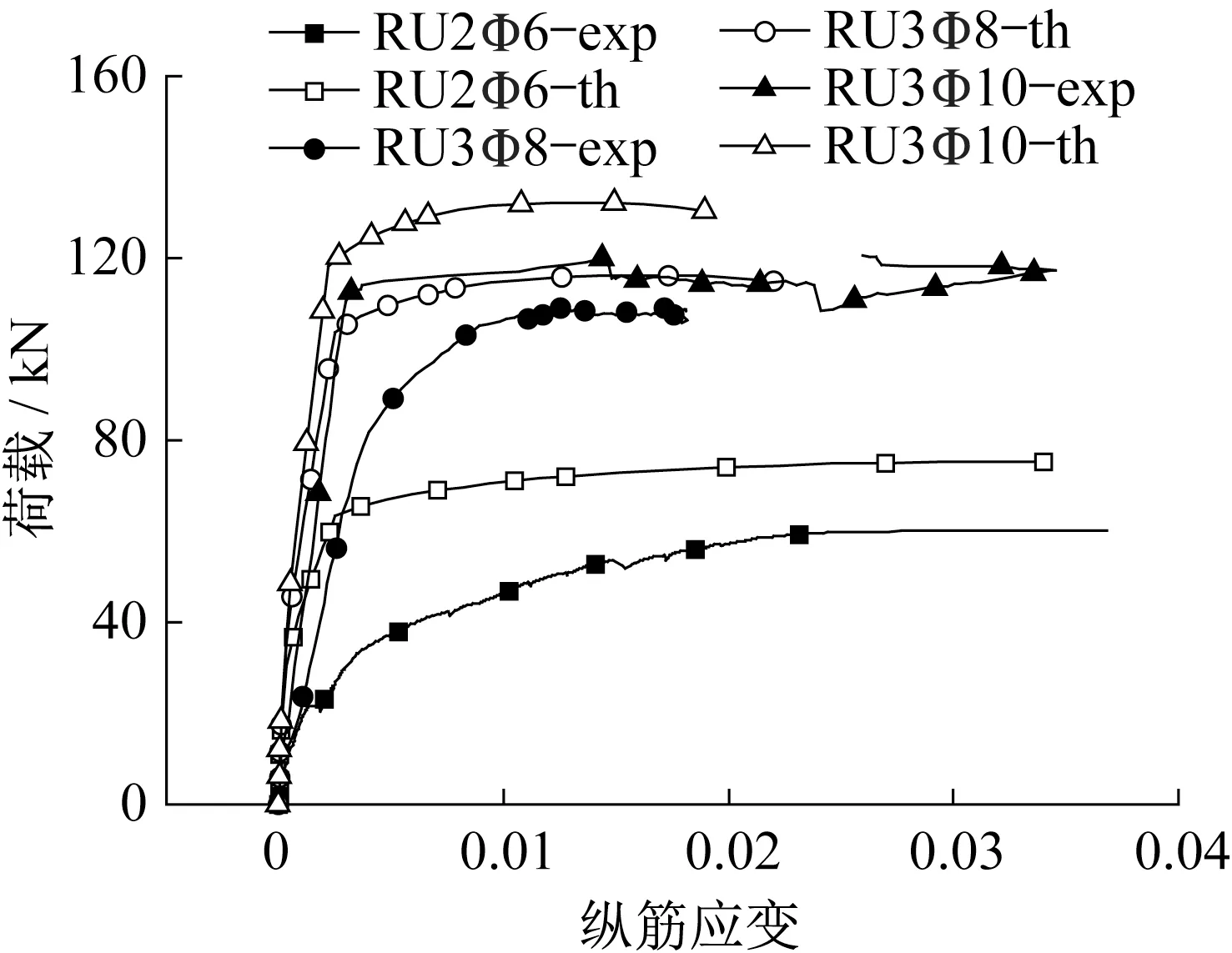
图13 荷载-纵筋应变的试验和理论计算结果Fig.13 Experimental and theoretical results of load and strain of longitudinal steel bars

图14 给出了荷载和HS-ECC 受压边缘应变的关系。对比RU3Φ8 的试验和理论计算曲线后可以发现，峰值荷载前DIC 观测的受压边缘应变与理论预测值较接近，但峰值荷载后DIC 观测的极限压应变更大，此时试件荷载并没有明显下降。纵筋屈服后受压边缘HS-ECC 应变发展更快，这与平截面假定有一定偏差。理论分析采用的HS-ECC轴心受压本构与受弯构件跨中截面顶部HS-ECC的受压本构有一定差异，实际受弯构件的跨中截面顶部HSECC处于偏心受压状态，受压边缘HS-ECC受到下部材料的约束，并将压应力有效传递给下部HSECC，因而相比均匀受压的HS-ECC 在更大极限压应变下受压边缘区HS-ECC 仍然保持较高的压应力，从而维持了较高的荷载。

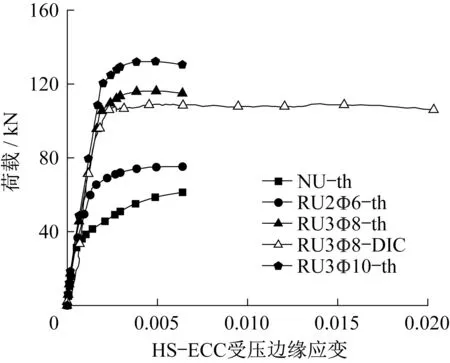
图14 荷载和HS-ECC受压边缘应变关系Fig.14 Relationship between load and compressive strain of HS-ECC

3.7 受拉区钢筋和HS-ECC对受弯承载力的贡献

配筋HS-ECC 受拉区拉力由钢筋和HS-ECC共同提供，受压区压力由HS-ECC提供，共同抵抗外力产生的弯矩。为了探讨配筋HS-ECC梁中钢筋和HS-ECC 对受弯承载力的贡献，以RU3Φ8 为例，将钢筋贡献的弯矩表示为钢筋拉力与钢筋合力中心到受压区HS-ECC 合力中心的距离的乘积，HS-ECC贡献的弯矩表示为总弯矩与钢筋贡献的弯矩之差，如图15a、b 所示。弹性阶段中性轴位置不变，HSECC和钢筋对弯矩的贡献比例分别为85%和15%。HS-ECC开裂后，钢筋贡献比例显著增加，在屈服前已超过HS-ECC，屈服时HS-ECC 和钢筋对弯矩的贡献比例分别为33%和67%。钢筋屈服后，凭借HS-ECC 优异的拉应变硬化性能，HS-ECC 对弯矩的贡献比例有所提升，试件破坏时HS-ECC 的贡献比例达到了37%。可见，HS-ECC 可有效提升构件的受弯性能。如图15c所示，随着配筋率的增大，各试件破坏时跨中截面弯矩中钢筋贡献比例逐渐增大，受拉区HS-ECC 的贡献比例逐渐降低。需要指出的是，受压区HS-ECC 的超高变形性能保证了受压区HS-ECC 不像普通混凝土那样发生压溃，使钢筋能够充分发挥受拉性能，提升了构件的弯曲承载力和延性。

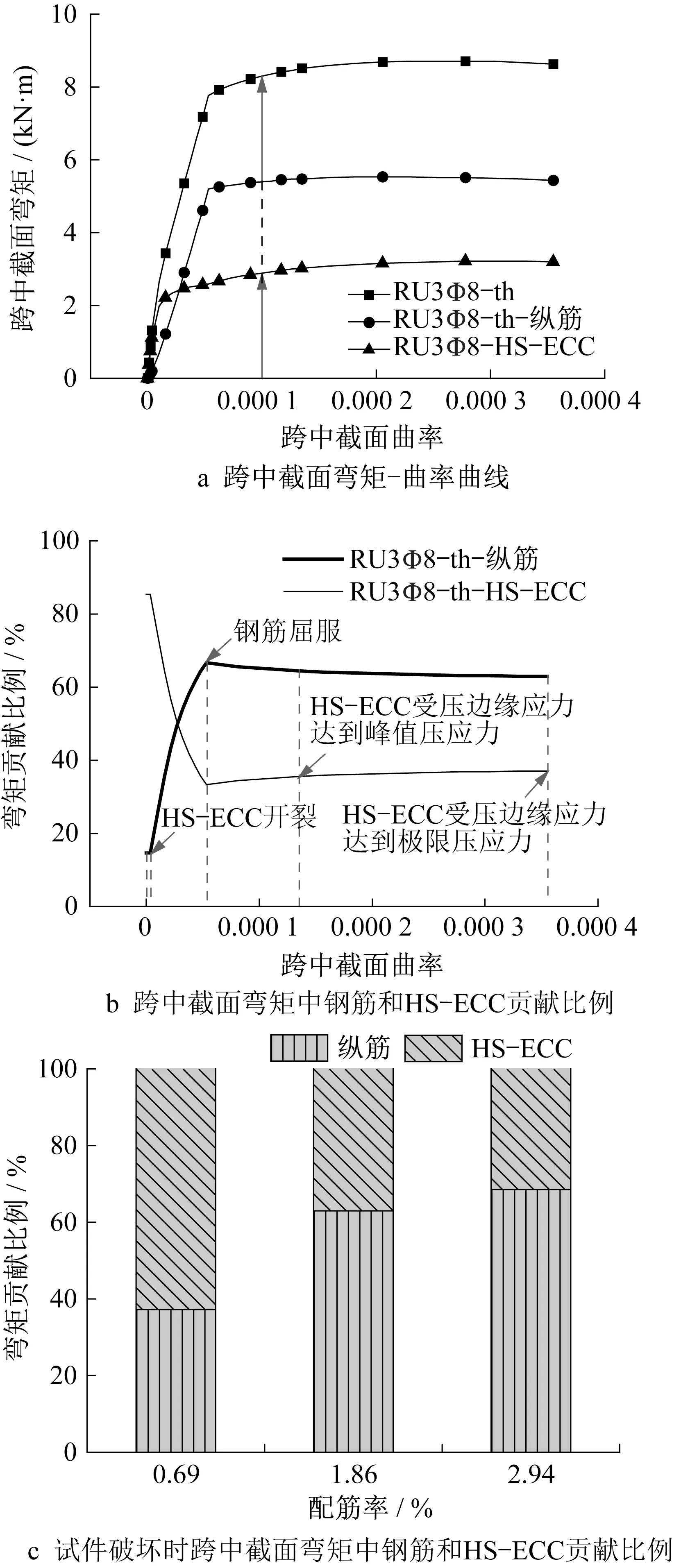
图15 受拉区钢筋和HS-ECC对跨中截面弯矩的贡献比例Fig.15 Contribution ratio of midspan moment for tensile longitudinal steel bars and HS-ECC

3.8 截面曲率延性系数、最小配筋率和界限配筋率

配筋HS-ECC梁的截面曲率延性系数与配筋率的关系如图16所示。随着配筋率的增大，截面曲率延性系数逐渐降低。一方面，增大配筋率提高了构件的抗弯刚度；另一方面，配筋HS-ECC梁的破坏仍以跨中顶部受压区HS-ECC达到受压极限压应变为标志，而受压区HS-ECC并未因配筋率增大而增强。因此，构件的截面转角变形能力降低，延性系数降低。

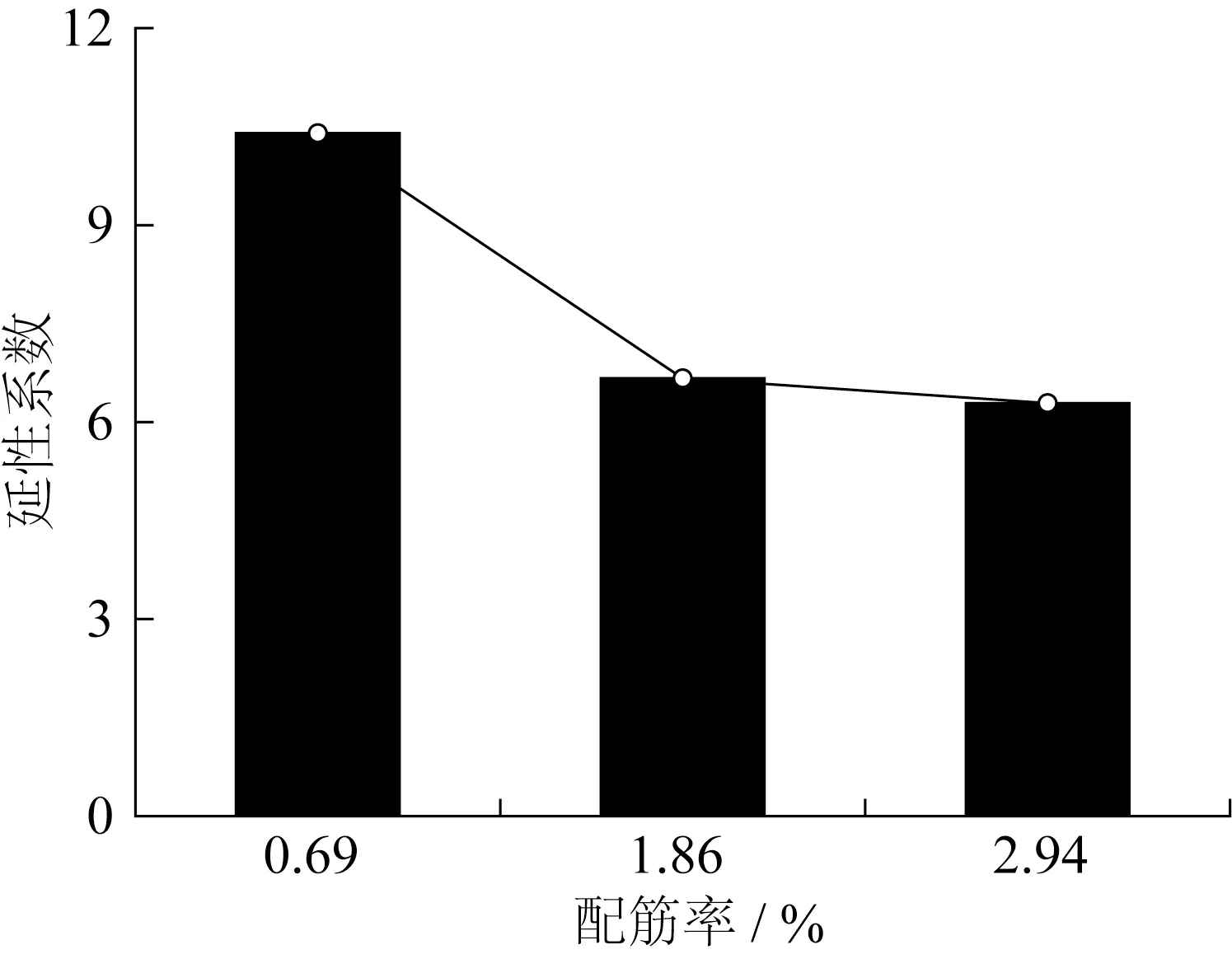
图16 截面曲率延性系数与配筋率的关系Fig.16 Relationship between cross-section curvature ductility index and reinforcement ratio

对于普通钢筋混凝土梁，当配筋率较小时，混凝土开裂后裂缝迅速扩展，开裂截面上原来由混凝土承担的拉力转嫁到钢筋，钢筋应力和应变迅速增大进而拉断，因此应对普通钢筋混凝土梁的最小配筋率做出规定。对于配筋HS-ECC 梁，当不配筋或配筋率较小时，HS-ECC 开裂后具有极强的拉应变硬化性能，能够继续承担拉力，不会导致钢筋应力陡增，因此一般不必对配筋HS-ECC 梁的最小配筋率做出限制。

当受拉钢筋应力达到屈服强度的同时，若HSECC 受压边缘纤维恰好达到极限压应变，则认为梁达到极限承载力而破坏，此时发生界限破坏，对应配筋率为界限配筋率。因此，根据力学平衡方程和几何物理关系（见式（29））可计算出界限配筋率。以直径为8 mm 的纵筋材性数据为例，将屈服强度500 MPa、弹性模量202 GPa代入式（30），可得界限配筋率ρmax=10.21%，因此本研究中3 根配筋HS-ECC受弯试件的配筋率均小于界限配筋率。

式中：xcu为界限破坏时中性轴到梁顶面距离。

4 受剪承载力计算

4.1 规范中的计算公式

如表5 所示，针对本研究中的无腹筋HS-ECC梁的受剪承载力，共采用4种规范进行计算，参数定义见对应规范。采用规范中的公式计算配筋HSECC 梁的受剪承载力时，材料强度和应变性能指标均取平均值，材料性能分项系数均取1.0。

表5 HS-ECC梁受剪承载力计算公式Tab.5 Calculation formula for shear capacity of HS-ECC beams

4.2 理论计算与试验结果对比

表6对比了试验和理论计算的受剪承载力。对于RU2Φ6NS，Vexp取试件受弯极限荷载的一半。除Vu3外，各理论受剪承载力均显著大于试验承载力，表明试件发生受弯破坏是合理的。对于Vu1与Vu4，由于不考虑纵筋影响，不同配筋率试件的理论受剪承载力均相等。纤维混凝土结构技术规程的计算结果Vu1略小于试验受剪承载力，偏于保守。日本JSCE2008规范（Vu2）考虑了纵筋配筋率的影响与纤维的桥联作用，理论计算值略大于试验值。法国AFGC规范（Vu4）同时考虑了剪压区混凝土和纤维的贡献，计算值显著大于试验受剪承载力，这主要是因为剪压区混凝土对受剪承载力的贡献过大。Fib model code for concrete structures 2010（Vu3）同样考虑了纵筋配筋率的影响和纤维的贡献，给出的理论计算值与试验值最为接近。因此，对于配筋HS-ECC梁受剪承载力计算，采用日本规范与Fib规范更合适。值得指出的是，关于HS-ECC的抗压强度和拉伸强度的取值均有待进一步讨论。

表6 HS-ECC梁的试验和理论受剪承载力Tab.6 Experimental and theoretical shear capacity of HS-ECC beams

5 基于Abaqus 软件的配筋HS-ECC梁受弯和受剪性能数值模拟

5.1 材料模型

采用Abaqus 有限元软件开展了配筋HS-ECC梁的受弯和受剪性能数值模拟。采用的HS-ECC受压本构关系参考了文献［28］建议的超高性能混凝土理论公式，如方程（31）和图17a所示。

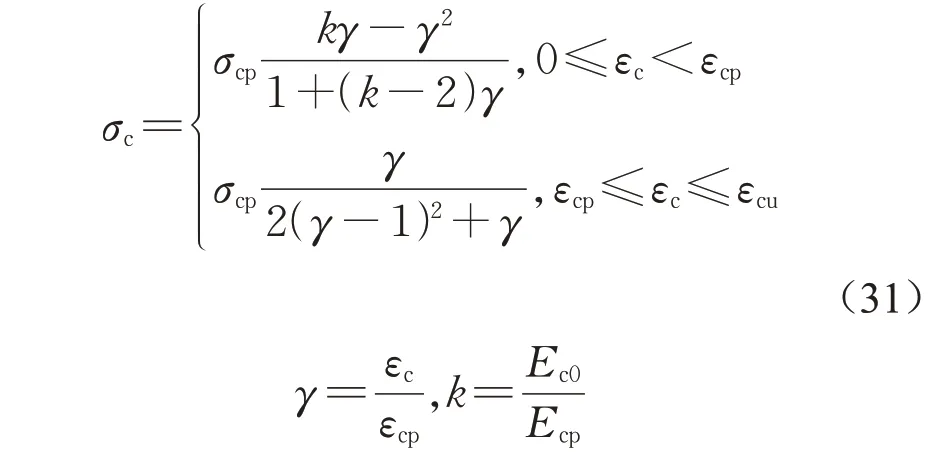
式中：Ec0为初始弹性模量；Ecp为峰值点的割线弹性模量。受压本构关系如图17a所示。对于HS-ECC的受拉本构关系，根据拉伸试验数据，补充拉伸下降段曲线，采用三折线本构关系，如图17b 所示。图17b中，σtd和εtd分别为材料破坏时拉伸应力和应变。

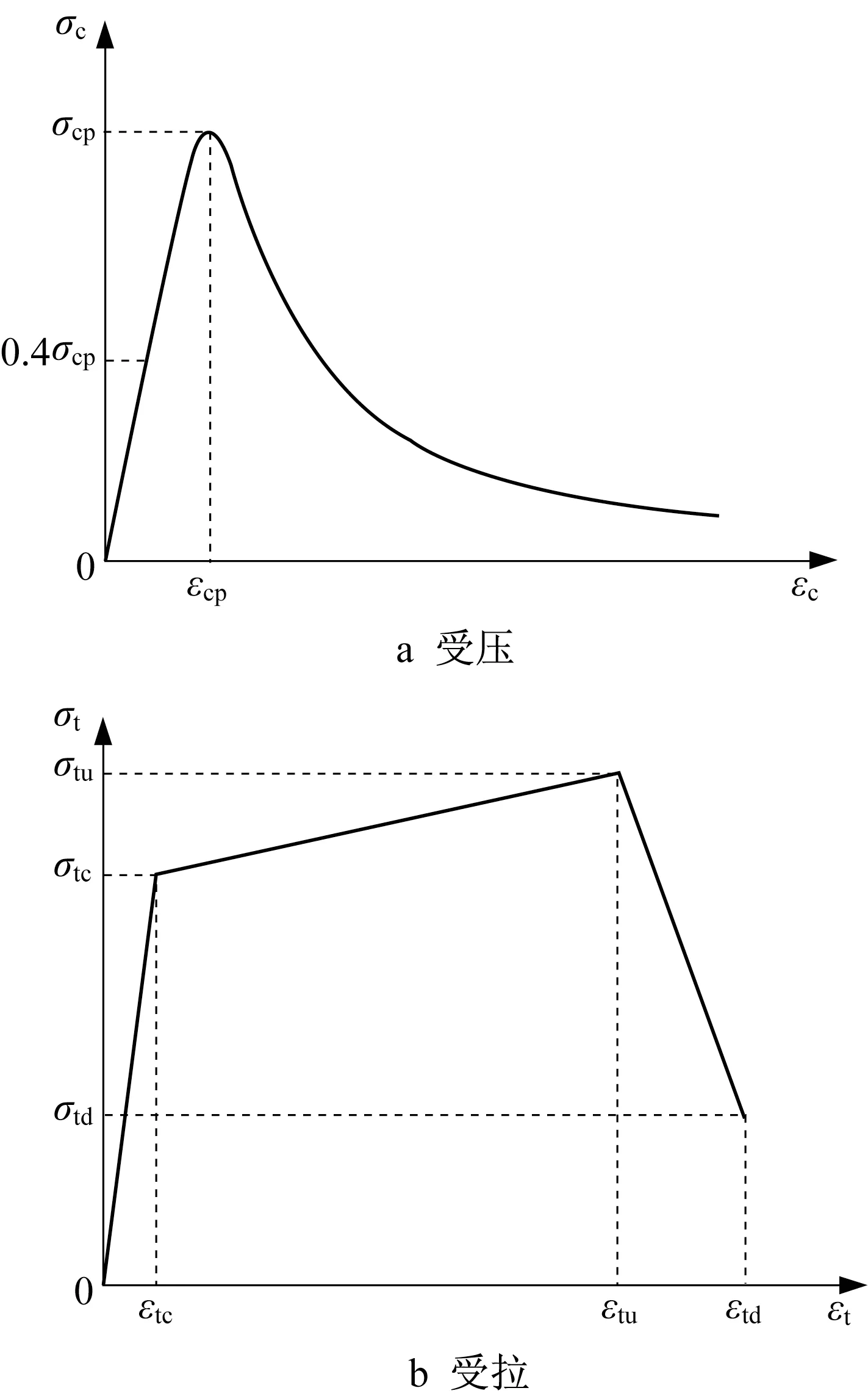
图17 有限元模型中HS-ECC的受压和受拉应力-应变曲线Fig.17 Theoretical compressive and tensile stressstrain curves of HS-ECC in finite element model

采用Abaqus 软件自带的混凝土塑性损伤（concrete damaged plasticity，CDP）模型作为HSECC 的材料模型。CDP 模型选用的HS-ECC 梁基本参数如表7、8 所示。损伤因子的计算参考文献［29］建议的虚交点法，受拉常数nt和受压常数nc分别取5.0和20.0。

表7 混凝土塑性损伤模型采用的HS-ECC梁基本参数Tab.7 Basic parameters of concrete damage plasticity model for HS-ECC beams

数值模型中钢筋的真实应力-应变曲线由试验结果的名义应力-应变曲线换算获得，如图18所示。

图18 有限元模型中不同直径钢筋的真实应力-应变曲线Fig.18 True stress-strain curves of steel bars with different diameters in finite element model

5.2 模型建立和验证

有腹筋HS-ECC梁的有限元模型和网格划分如图19所示，无腹筋HS-ECC梁的有限元模型在有腹筋模型基础上去掉箍筋和架立筋。数值模型的网格划分如表9 所示。为了使纯弯段更好地表现出应力-应变分布变化，将梁高方向尽量划分较多的层，本研究中取16层。

表8 HS-ECC梁采用的材料力学性能参数Tab.8 Mechanical parameters of material for HS-ECC beam

表9 有限元模型的网格划分Tab.9 Meshing of finite element model

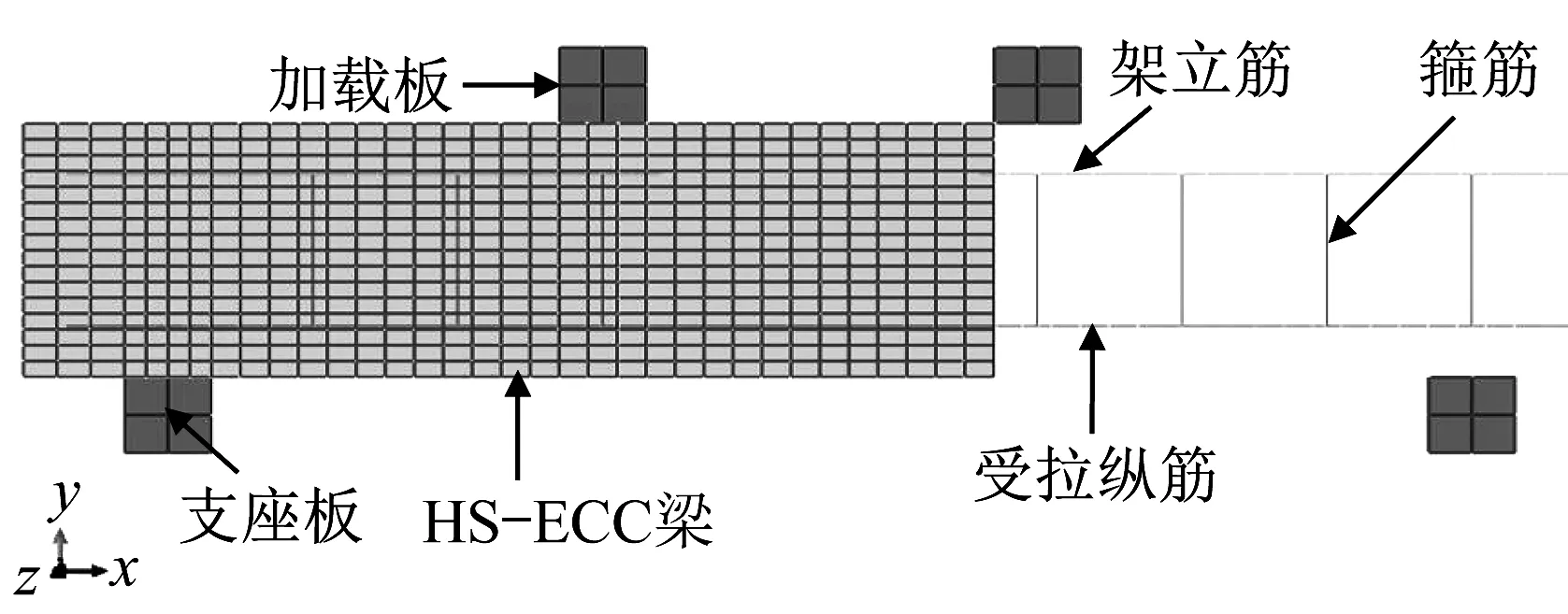
图19 基于Abaqus软件的配筋HS-ECC梁的有限元模型Fig.19 Finite element model of HS-ECC beams based on Abaqus

加载板与HS-ECC 梁之间法向采用硬接触（hard contact），切向采用摩擦接触，摩擦系数取0.25。支座与HS-ECC梁之间采用Tie约束。钢筋与HS-ECC 梁之间采用Embeded连接，不考虑两者的黏结-滑移关系。采用位移控制施加荷载，设置参考点并耦合至加载板顶面。

5.3 模拟结果

5.3.1 荷载-跨中挠度曲线

图20给出了各试件的试验（exp）与有限元模拟（num）的荷载-跨中挠度曲线。如图20a 所示，对于未配筋梁，模拟的荷载-跨中挠度曲线与试验曲线吻合较好，仅承载力略低，刚度和最大位移接近。如图20a、b所示，对于有腹筋和无腹筋HS-ECC梁，模拟荷载-跨中挠度曲线与试验曲线吻合良好，但由于未考虑钢筋与HS-ECC的黏结-滑移关系，模拟曲线的初始刚度普遍较试验曲线略大。

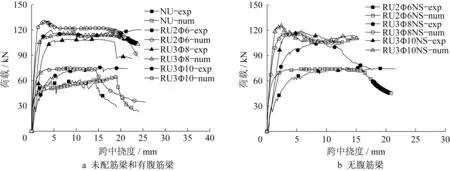
图20 试验和有限元模拟的荷载-跨中挠度曲线Fig.20 Numerical and experimental load-midspan deflection curves

5.3.2 极限承载力

由表10 可知，对于未配筋HS-ECC 梁，有限元模拟所得最大荷载略大于试验值和理论值；对于有腹筋梁和无腹筋梁，模拟最大荷载均略大于试验值和理论值，平均误差小于10%，在可接受范围内。基于Abaqus 软件的有限元模型能够有效模拟配筋HS-ECC 梁的受弯和受剪性能，为今后进一步参数分析奠定了基础。

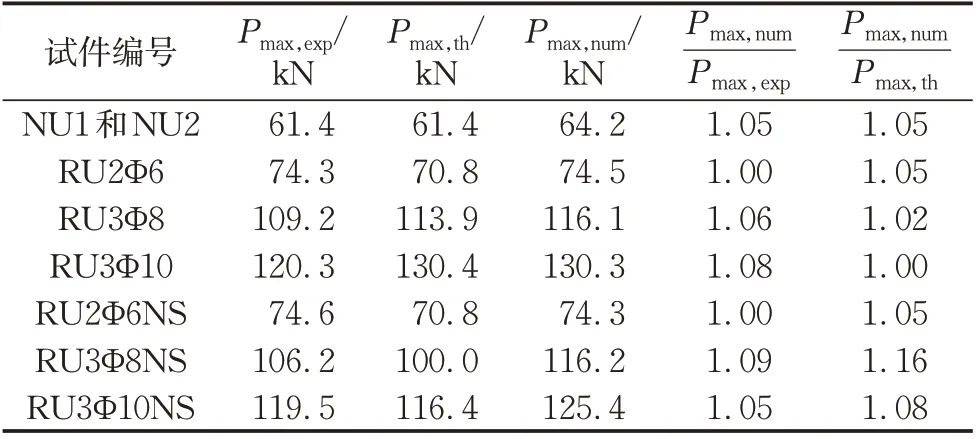
表10 试验、理论和数值模拟的最大荷载对比Tab.10 Comparison of experimental, theoretical and numerical maximum load

6 结论与展望

（1）配筋HS-ECC梁充分发挥了HS-ECC优异的拉伸与压缩变形能力，从而表现出优异的弯、剪延性以及更高的承载力与刚度。HS-ECC具有高拉伸强度、高压缩变形能力以及良好的延性和裂缝控制能力，使其具备了独立承担荷载以及形成无配筋构件的能力，从而为极端环境下构件耐久性提升提供了潜在的解决方案。

（2）考虑了HS-ECC 尺寸效应与箍筋干扰引起的拉伸性能折减，推导的受弯承载力理论结果与试验结果吻合良好。随后，得到了截面弯矩-曲率关系、中性轴发展过程、不同配筋率下受弯构件对HSECC的拉应变需求，分析了钢筋和HS-ECC对受弯承载力的贡献，并计算了截面曲率延性系数和界限配筋率。最后，验证了现有规范对无箍筋HS-ECC梁剪切承载力的适用性。

（3）基于Abaqus软件的有限元模型准确模拟了HS-ECC弯剪试件的荷载-跨中挠度曲线，试件的模拟最大荷载与试验值平均误差小于10%。

作者贡献声明：

蔡自伟：论文构思、写作和修改，理论推导。邓博予：试验实施，数据整理。张 智：数值模拟。陆洲导：基金获取。李凌志：基金获取，论文修改。俞可权：试验方案提出。