弹性需求的Logit随机共乘用户均衡模型和算法

马 捷，李 锐，王 华

（1. 东南大学交通学院，江苏南京 211189；2. 道路交通工程国家级实验教学示范中心（东南大学），江苏南京 211189；3.河海大学土木与交通学院，江苏南京 210024；4. 新加坡国立大学土木与环境工程系，新加坡 117576）

随着共享经济的兴起，共享出行成为当前城市交通网络的重要出行方式［1］，共乘出行（即顺风车出行等）作为共享出行的典型形式之一也受到广大交通出行者的青睐［2-3］。共乘出行是指具有共同出行起讫点的出行者们通过网约车平台进行匹配并分别成为共乘驾驶员和共乘乘客，乘客通过支付一定补偿费用给驾驶员从而分担出行费用的一种出行方式，可在降低出行者出行费用的同时满足出行者的出行需求［1］。虽然共乘出行占当前城市交通网络中机动车的出行比例仍较低，但是由于城市交通网络的复杂性，共乘出行交通方式已经极大地改变了城市交通网络的结构和出行者的出行需求［4］。交通流量是交通网络中最重要的变量之一，建立城市交通网络模型是预测和分析交通流量的重要手段。通过城市交通网络建模，可以实现交通规划和管理的诸多功能，如制定共乘价格、估计通行时间、设计交通网络等。因此，建立考虑了共乘出行的城市交通网络模型，分析共乘出行对交通流量的影响，量化出行费用对出行需求的影响程度，这将有力地支撑共乘出行城市交通系统的科学规划与设计。

考虑了共乘出行的城市交通网络（下文简称共乘交通网络）的出行用户分为3类：单独出行的驾驶员（即传统私人小汽车出行方式的出行者）、共乘驾驶员和共乘乘客。共乘驾驶员和共乘乘客通过网约车平台实现匹配，乘坐共乘驾驶员的车辆出发并到达目的地。未参与或未成功实现匹配的用户将作为单独出行的驾驶员（即传统私人小汽车出行方式）独自完成出行。共乘交通网络中的出行者是存在转移关系的，即数量不是固定不变的。例如，当单独出行的驾驶员发现共乘驾驶员（或共乘乘客）的综合出行成本更低时，将放弃单独出行而选择成为共乘驾驶员（或共乘乘客）。由此产生的流量变化受到相互作用的综合出行成本、供需关系以及出行者选择行为的影响，是用户自由选择的结果，因此无法通过交通调查的方式获得。同时，与传统出行方式不同，共乘出行用户的交通流量之间还存在制约关系，这是因为共乘乘客的流量不能小于共乘驾驶员的流量，也不能大于共乘车辆的最大容量。此外，交通流量的这种约束还可能为模型带来新的乘子，导致传统交通分配算法的失效。以上原因为共乘交通网络建模带来了巨大的挑战［5］。Xu等［5］建立了首个共乘出行的交通分配模型，即共乘出行用户均衡（RUE）模型。该模型描述了共乘驾驶员和共乘乘客之间的流量关系，但只能计算单一的共乘服务，无法细化不同种类共乘服务的用户流量。Ma 等［6］提出了共乘出行的浮动定价策略和共乘匹配约束，并改进了RUE 模型，用以计算和预测多种共乘服务的出行流量。

然而，现有的RUE模型均假设用户完全掌握出行费用的全部信息，而现实中用户对出行费用的感知具有随机性［7-9］。此外，用户的出行需求也不是固定不变的，受到出行费用的影响［10-12］，而现有RUE模型假设需求是固定不变的。因此，考虑用户对出行费用感知的随机性以及出行费用对出行需求的影响是当前共乘交通网络研究的难点。

基于Logit选择模型和弹性需求函数，构建考虑弹性需求的Logit 随机共乘用户均衡（SRUEED）问题的变分不等式模型，保证模型解的唯一性。然后，采用全局最优的自适应并行投影算法求解了SRUEED 问题，该算法通过并行计算的方式极大地降低了内存需求和计算时间，提高了计算可行性。最后，通过2个算例验证了算法的有效性，并通过敏感性分析得到了共乘出行需求和平均出行时间的影响因素。

1 共乘交通网络

1.1 流量守恒

首先，建立共乘交通网络G=(N，A)，其中N表示网络节点的集合，A表示路段的集合；然后，分别建立单独出行的驾驶员、共乘驾驶员和共乘乘客的集合Ds、Dr和R，并建立泛指各类用户的集合I，即I=Ds∪Dr∪R。此外，每个类别的用户还可以包含不同的角色。例如，如果共乘驾驶员最多允许搭乘2名乘客，就可以令i=1 ∈Ds表示单独出行的驾驶员，i=2，3 ∈Dr分别表示搭载了1 名乘客和2 名乘客的共乘驾驶员，i=4，5 ∈R则分别表示共乘驾驶员i=2，3 所搭载的乘客。出行的起讫点分别用O和D 表示，共乘交通网络中3 类用户之间的关系如图1所示。

令w∈W表示出行起讫点对（即O-D 对），p∈Pw表示连接O-D对w的路径，qw表示O-D对w之间的出行需求，fw，p，i表示路径p上角色i的流量，xa和xa，i分别表示路段a∈A上的车流量和路段a上角色i的流量。共乘交通网络具有如下交通流量守恒关系：

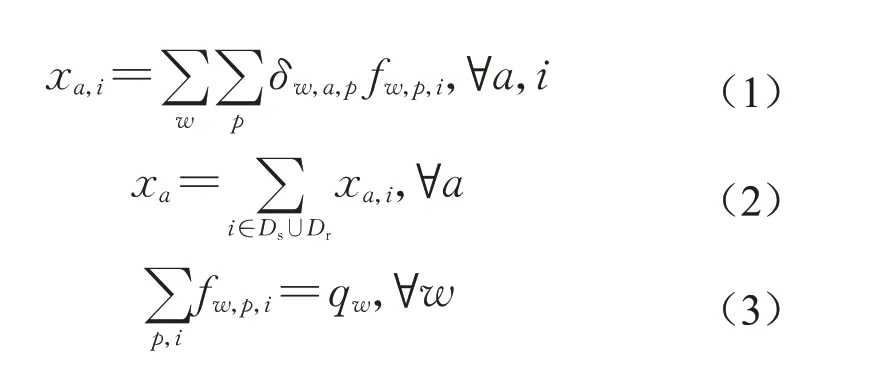
式中：δw，a，p表示路段-路径关联变量。当路段a属于路径p时，δw，a，p=1，否则δw，a，p=0。

1.2 共乘匹配约束

由于共乘驾驶员需要匹配共乘乘客才能完成共乘出行，因此共乘驾驶员与共乘乘客之间始终保持着显式的数量关系［6］。Ma等［6］由此提出了以下共乘匹配约束：

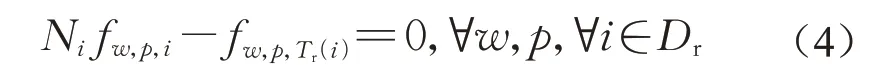
式中：Tr(i)表示共乘驾驶员i接乘的乘客，Tr(2)=4表示共乘驾驶员类型2所接乘的乘客类型4；Ni表示共乘驾驶员i分享的座位数。

1.3 广义出行费用

共乘出行涉及多种出行费用，部分文献将出行费用总结为以下几类：出行时间费用、不便费用、共乘价格和报酬以及溢价和补贴。其中，溢价和补贴与共乘出行服务的供需相关，因此溢价和补贴以外费用的总和称为出行费用，出行费用加上溢价和补贴称为广义出行费用［5-6，13］。由于研究的是随机共乘均衡问题，因此不涉及具体的广义出行费用函数的设计。广义出行费用采用文献［6］给出的一般形式，如下所示：

令x=(xa，a∈A)T表示路段a上车流量向量，f=(fw，p，i，w∈W，p∈Pw，i∈I)T表示路径p上角色i流量向量，用tw，p(x)表示路径p的出行时间，则有

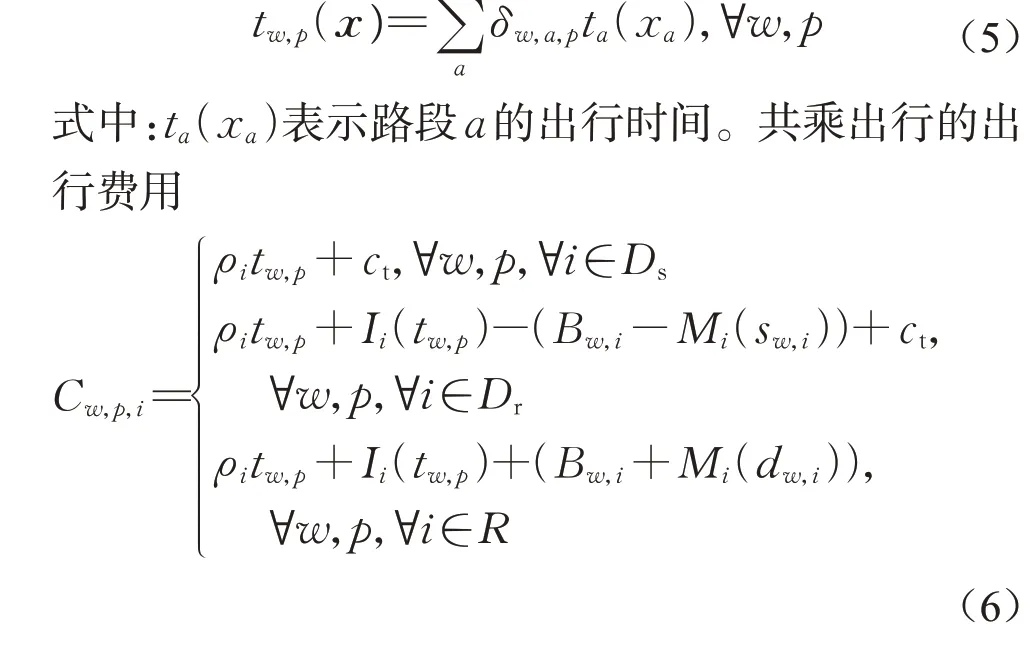
式中：ρi表示角色i的时间价值；Ii(tw，p)表示角色i的不便费用，该费用与出行时间和共乘人数有关，出行时间越长或共乘人数越多则不便费用越大，因此不便费用是出行时间tw，p的单调递增函数，并且由于每种共乘出行服务都有各自不同的共乘人数，因此每种角色i都有各自适用的不便费用函数Ii(tw，p)；Bw，i表示共乘出行的基准价格（或报酬），该价格（或报酬）与O-D对w和角色i有关，对于共乘驾驶员来说该项费用表示共乘报酬，对于乘客来说该项费用表示共乘价格；Mi(sw，i)表示浮动报酬，是共乘出行供给的单调递减函数，即O-D对之间的共乘驾驶员越多则平均浮动报酬越低；Mi(dw，i)表示浮动价格，是共乘出行需求的单调递增函数，即O-D对之间的乘客越多则平均浮动价格越高；ct表示与出行时间和里程无关的固定费用，如购车费用、保险费用、停车费用等。

根据经济学市场出清原理［5］，共乘出行的溢价和补贴与供需平衡有关，并且数值上刚好等于共乘匹配约束所对应的拉格朗日乘子。因此，共乘出行的广义出行费用

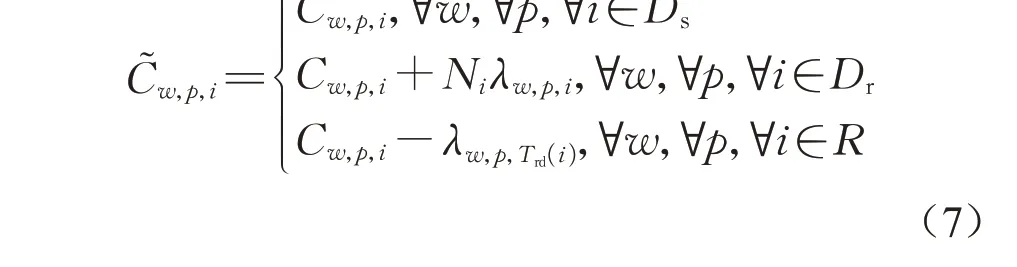
式中：λw，p，i表示共乘匹配约束（4）所对应的拉格朗日乘子；Trd(i)表示接乘共乘乘客i的共乘驾驶员类型。C͂w=(C͂w，p，i，p∈Pw，i∈I)T，w∈W表示O-D 对w的广义出行费用向量。

2 弹性需求的Logit 随机共乘用户均衡条件

2.1 基于Logit的随机共乘用户均衡

由于网约车公司会为共乘驾驶员和共乘乘客提供共乘报价，因此共乘出行的价格和报酬较为精确，但共乘用户感知的出行时间是不确定的，广义出行费用的随机性主要来自于实际出行时间的不确定，因此感知的广义出行费用是一个随机变量，表达式如下所示：

式中：θ为用户感知离散参数，θ=π/ 6σ。θ越大表示分布的方差越小，用户对广义出行费用的感知越精准。

2.2 弹性需求

现实中的出行需求并不是固定不变的，城市交通网络以及交通行为选择领域中许多成熟的研究表明，出行需求与平均服务水平正相关，与用户感知的最小广义出行费用的期望负相关［17-20］。由于出行需求最大不能超过出行人数、最小不为负数，因此出行需求会受上下界的约束。根据城市交通网络的相关研究成果［17-20］，采用Sw表示用户感知的最小广义出行费用的期望值并建立弹性需求函数，如下所示：

式中：qˉw为常数，表示出行需求的上界；ew(Sw)是关于Sw的单调不增的连续可微函数。

由式（8）可知，用户感知的广义出行费用是一个随机变量，因此最小用户感知的广义出行费用也是一个随机变量。根据期望的定义对Logit 选择模型的用户感知最小广义出行费用进行推导［19］，可知

3 弹性需求的Logit 随机共乘用户均衡模型

接下来，验证该模型的解的等价性、存在性以及唯一性，即该模型的解符合弹性需求的Logit随机共乘用户均衡条件、解存在并且是唯一的。

定理1（等价性）模型（16）的解符合弹性需求的Logit随机共乘用户均衡条件。

证明：模型（16）显然等价于

即弹性需求的Logit 随机共乘用户均衡条件。命题得证。

此处注意，虽然数学规划（18）与模型（16）等价，但是由于f*未知，导致数学规划（18）没有显式表达，因此无法直接作为模型。

2.5.1 创面出血 术中严格止血、确认无活动性出血后方能结束手术。拔除尿管前轻度出血可暂时观察并行膀胱冲洗，牵拉尿管以压迫电切创面。如果术后出现下列情况，应急诊在电切镜下清除血凝块并重新止血：①膀胱冲洗液颜色突然变红，经牵拉气囊无缓解；②血红蛋白持续性下降；③出现血压显著下降及心率显著加快；④膀胱内血凝块形成，经常规抽吸无法恢复冲洗通畅。术后1～3个月内应避免刺激性食物及剧烈活动，保持大便通畅。如出现轻度血尿，嘱患者多饮水，严重出血或形成膀胱内血肿时处理同围手术期。

定理2（存在性）模型（16）的解存在。

证明：由集合Ω的定义可知，Ω是一个紧集。由于函数φ( )· 在紧集Ω上连续，因此根据Nagurney 的定理1.4可知［6］，变分不等式模型（16）的解存在。命题得证。

定理3（唯一性）模型（16）的解唯一。

证明：首先计算向量函数φ(f)的Jacobian 矩阵，如下所示：

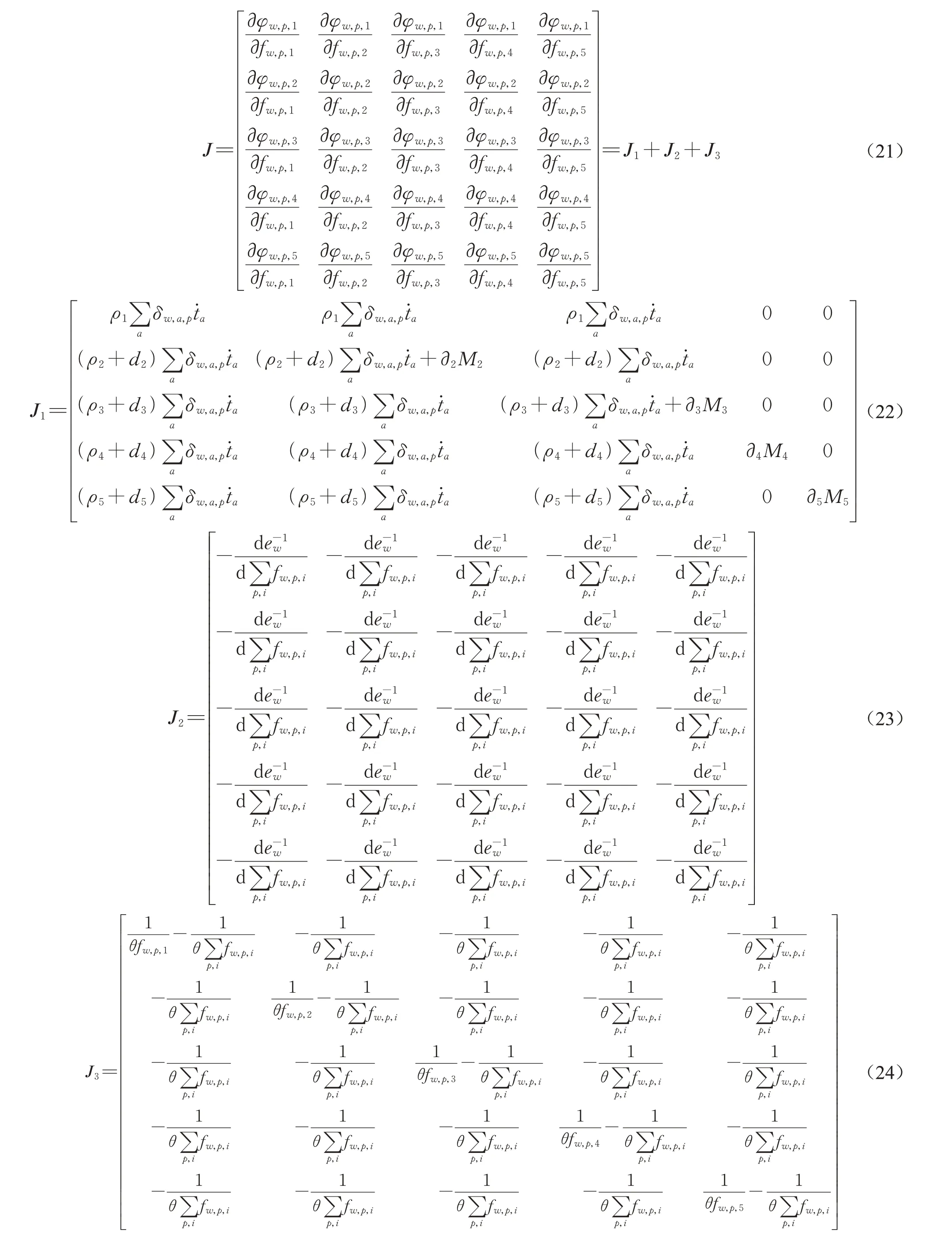
因此，根据矩阵半正定的判定条件，J3也是半正定的。由J=J1+J2+J3可知J正定，即向量函数φ(f)关于向量f单调。根据Pang 和Facchinei 的定理2.3.3（a）［6］可知，模型（16）的解唯一。命题得证。

4 自适应并行投影算法

在证明了研究问题的解存在且唯一之后，基于全局最优的自适应投影算法［22］，提出自适应并行投影算法并对该问题进行求解。由于城市交通网络往往规模较大，现有的算法难以求解，因此基于并行计算的思想将原问题按照O-D 对分解成若干个子问题，每个子问题求解一个O-D 对的路径流量，最后将各个O-D对的路径流量解合并即为原问题的解。相比于自适应投影算法，所提出的算法极大地减少了对内存的占用，适合求解大规模的交通分配问题。此处定义可行集里到向量最近的点为该向量在可行集上的投影，即：

该算法的收敛性证明详见He等［22］的证明。下文将通过文献中常用的2个城市交通网络Braess网络和Sioux-Falls网络算例对上述模型和算法进行验证。

5 算例研究

采用2 个城市交通网络算例验证弹性需求的Logit 随机共乘用户均衡模型和自适应并行投影算法。算例中使用的广义出行费用函数的具体形式如式（38）所示，弹性需求函数如式（39）所示，模型和算法中相关参数的具体数值如表1所示。

表1 参数设置Tab.1 Parameter settings

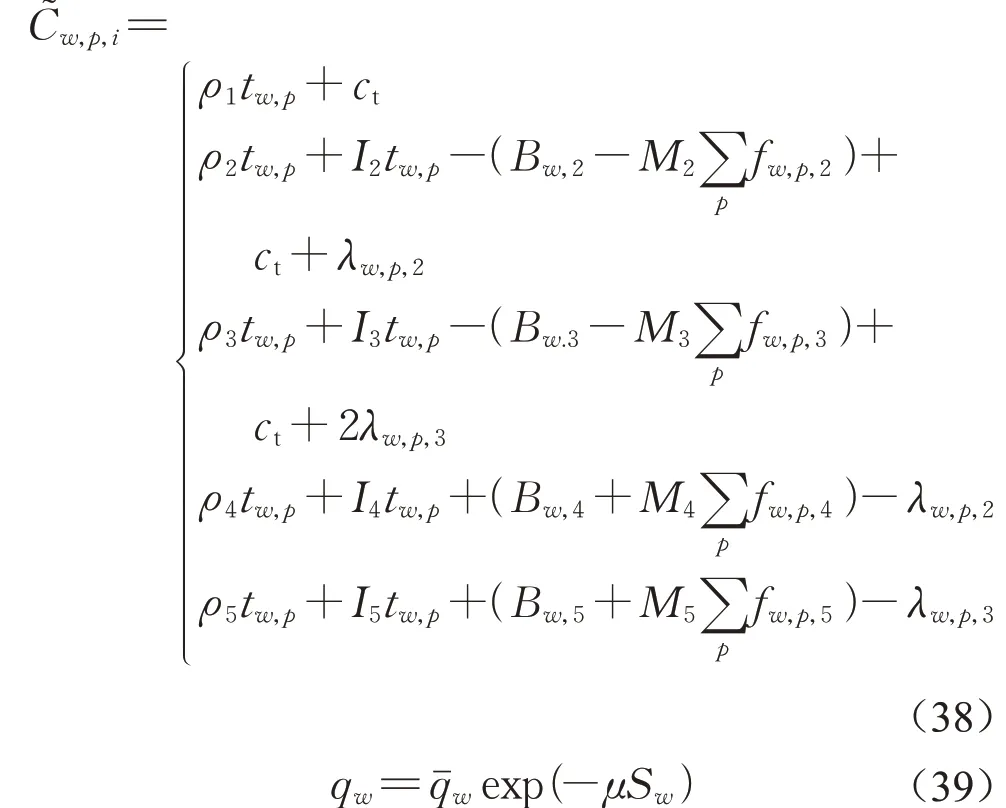
式中：μ为弹性需求参数。

5.1 Braess网络

Braess 网络出行需求的上界qˉ=6，拓扑结构以及各条路段的出行时间函数如图2 所示，x1～x5和t1～t5分别表示Braess 网络中各路段的流量和出行时间。对弹性需求参数和用户感知离散参数进行敏感性分析。

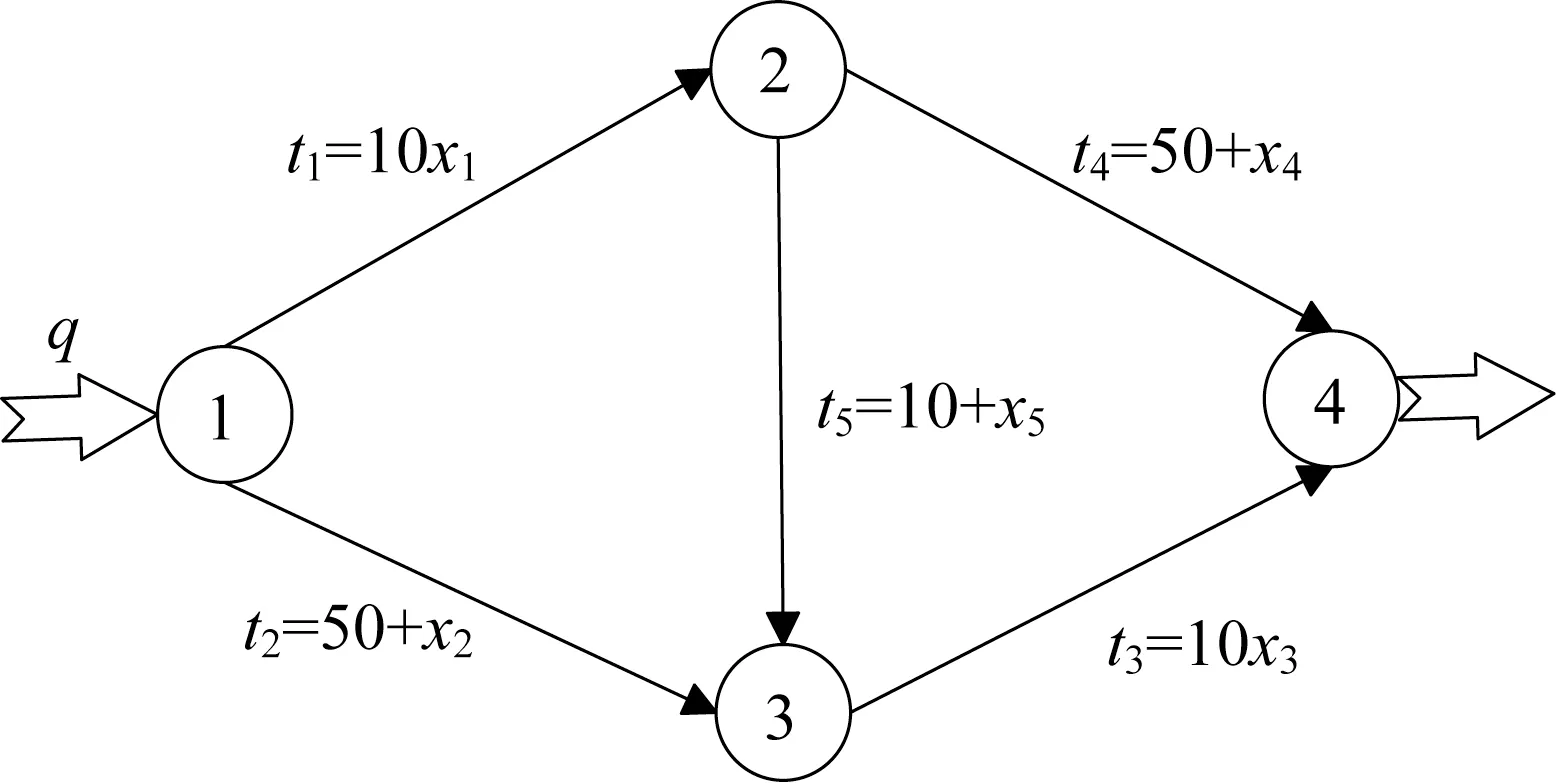
图2 Braess网络Fig.2 Braess network

弹性需求参数μ的敏感性分析如图3 所示。结果表明，随着用户的出行需求对出行费用的敏感度增加，出行需求和平均出行时间降低。这是因为用户对交通拥挤的厌恶驱使用户选择其他出行方式或放弃出行。研究表明，交通拥挤的大城市的用户对出行费用更为敏感［24］。由于共乘出行在满足出行需求的同时减少了道路上的车流量，缓解了交通拥挤，因此在大城市中发展共乘出行更易得到共乘用户的支持。

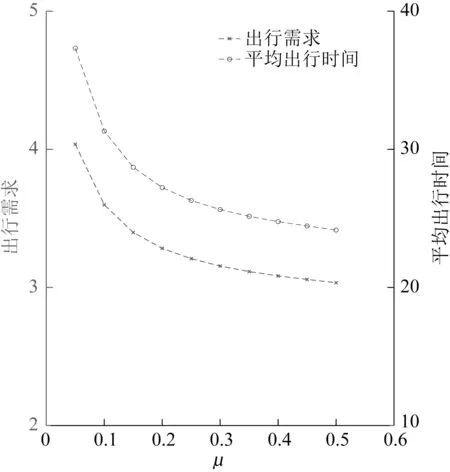
图3 弹性需求参数的敏感性分析Fig.3 Sensitivity analysis on elastic demand parameter

用户感知离散参数θ的敏感性分析如图4所示。结果表明，用户对出行费用的感知越精确，出行需求和平均出行时间就越小。因此，如果用户配备了导航或其他先进的出行信息系统，平均出行时间就会减少，交通拥堵就会得到明显缓解。由于网约车平台会为共乘出行提供出行信息和导航信息，因此共乘出行的普及将会有利于交通拥堵缓解。

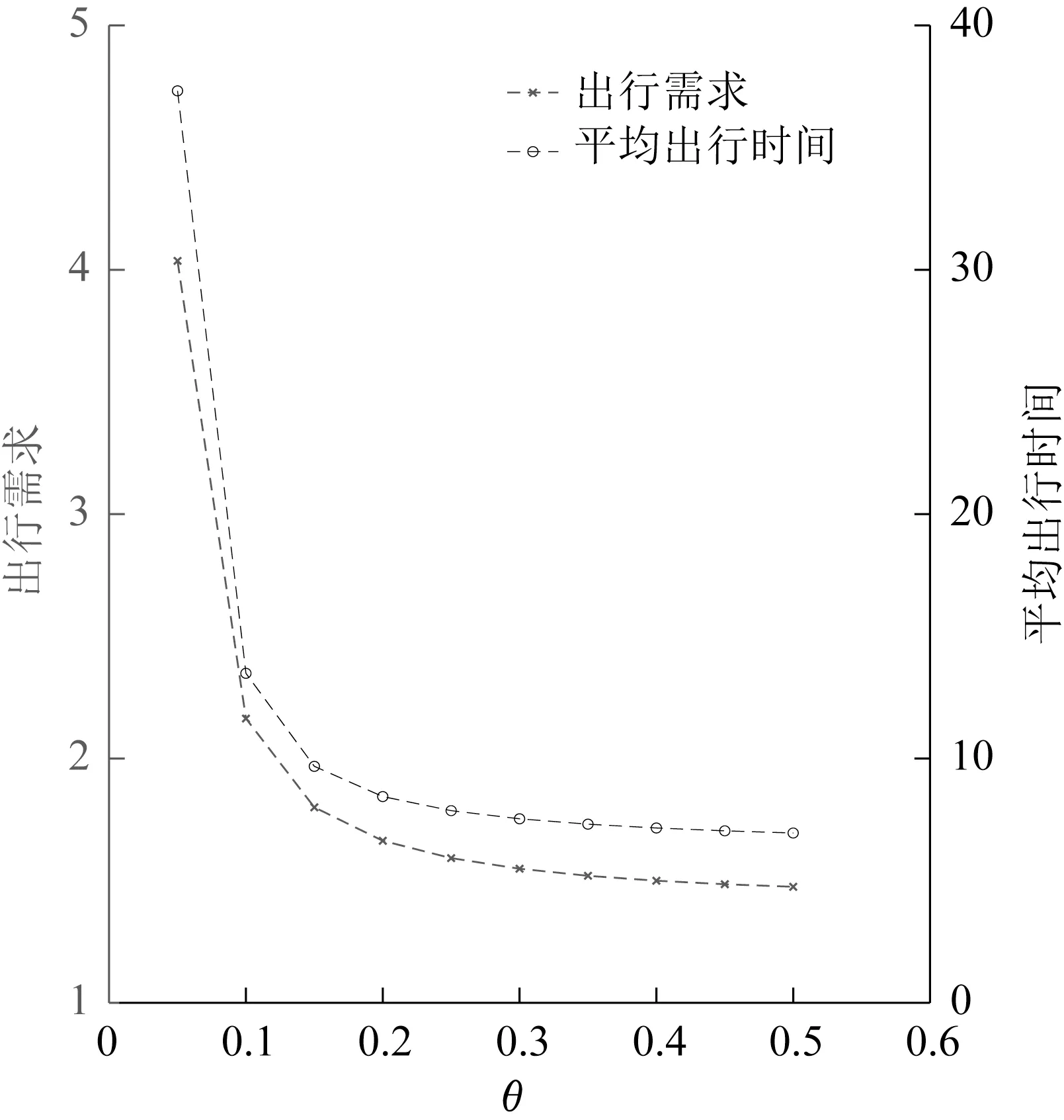
图4 用户感知离散参数的敏感性分析Fig.4 Sensitivity analysis on user perception dispersion parameter

5.2 Sioux-Falls网络

由于城市交通网络问题通常是一个大规模问题，计算交通流量的全局最优解往往需要消耗大量的计算资源和计算时间，因此采用一个大规模城市交通网络Sioux-Falls网络对算法的计算可行性进行验证。Sioux-Falls 网络的拓扑结构如图5所示。该网络的路段出行时间函数以及出行需求的上界qˉw详见文献［6］，其他参数设置与表1一致。用K短路算法［23］为每个O-D 对寻找10 条最短路径作为路径集Pw。自适应并行投影算法用时1.24 h达到1%的精度，该网络路段流量的实验结果如表2所示。

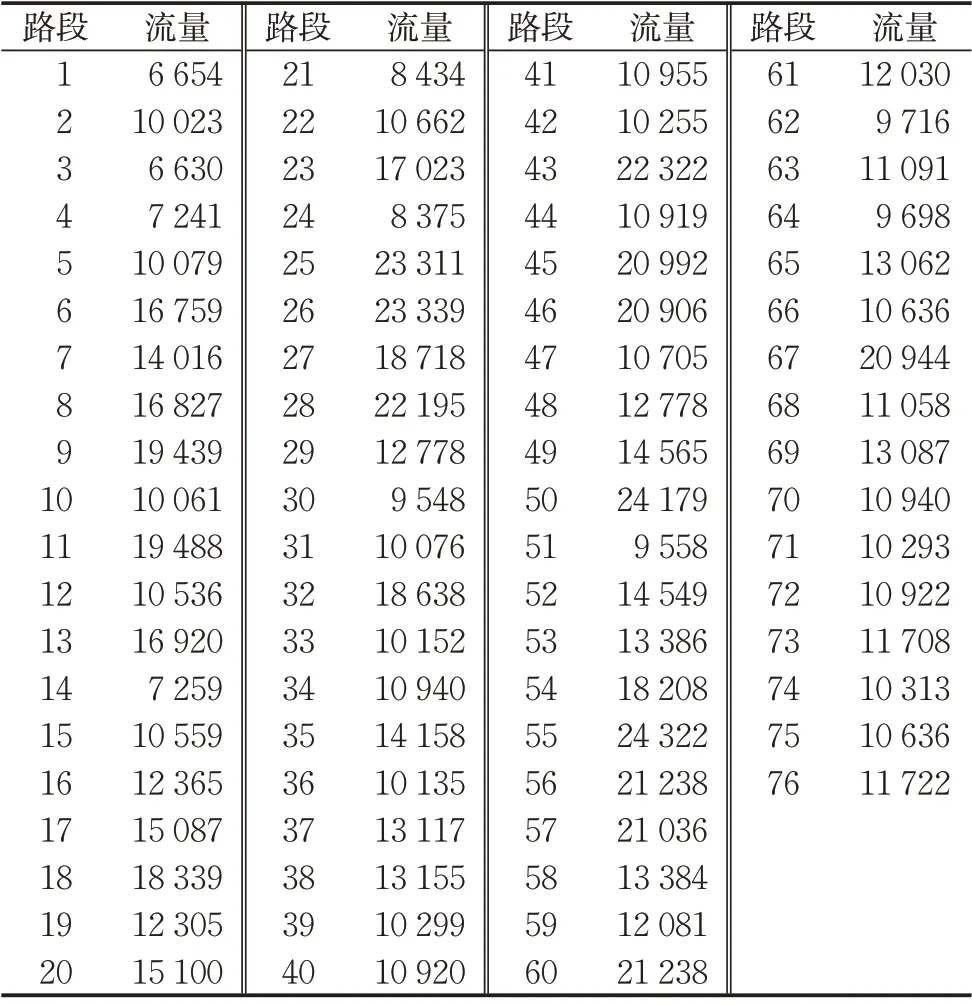
表2 Sioux-Falls网络的路段流量Tab.2 Link flow of Sioux-Falls network

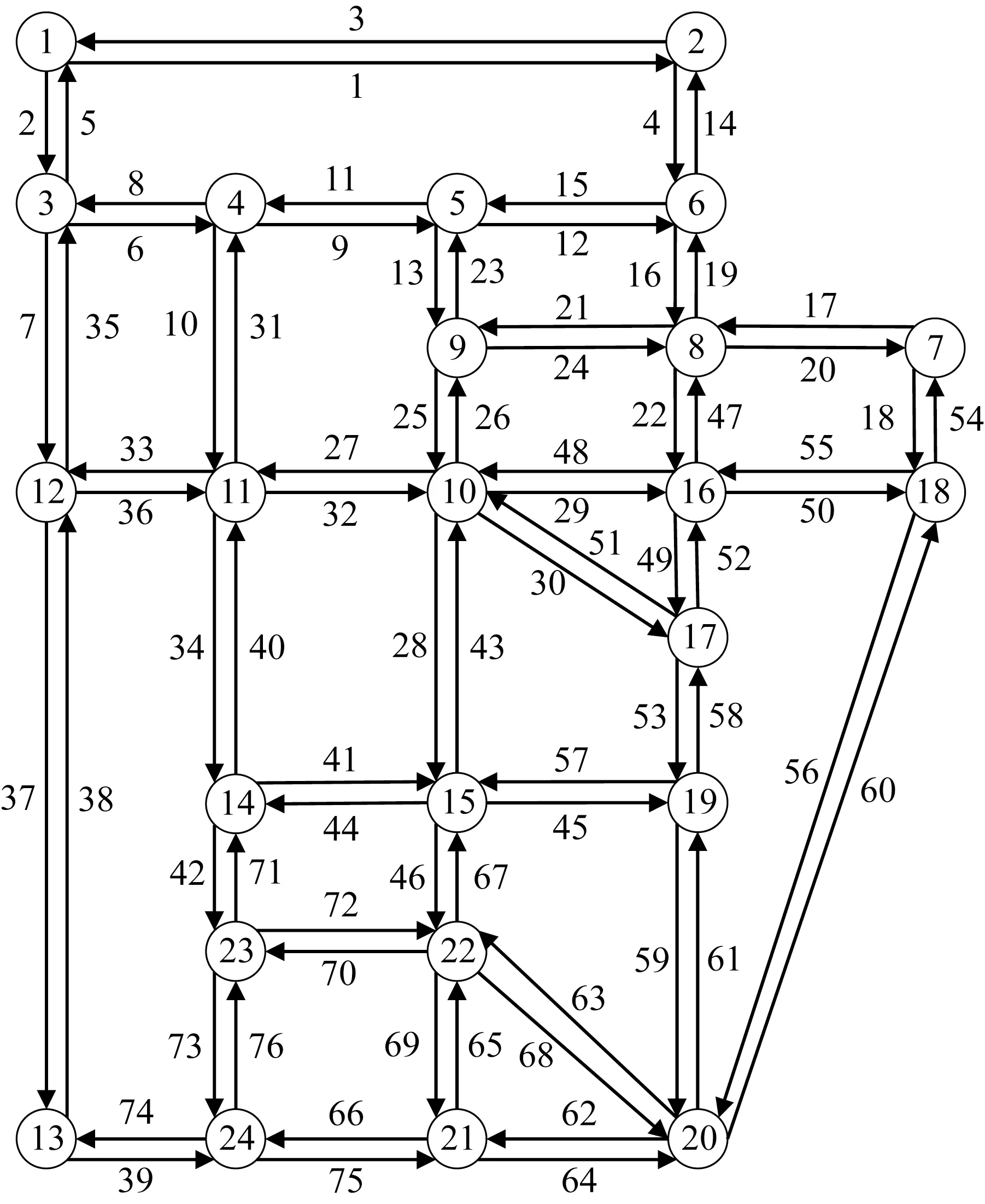
图5 Sioux-Falls网络Fig.5 Sioux-Falls network

表3显示了各类出行角色在Sioux-Falls网络中的总流量，反映了在当前选取的参数下网络中大部分出行者仍然是单独出行的驾驶员。本算例中，Sioux-Falls网络的共乘出行者与现实网络相比比例偏高，这是因为本算例仅为验证所提出的方法，所以采用的参数是随机的。在工程应用中可以获取具体城市交通网络关键参数的准确值从而得到精确的流量预测结果。

表3 Sioux-Falls网络的出行角色流量Tab.3 Role flow of Sioux-Falls network

6 结语

通过分析用户出行需求与出行费用的相互作用关系，建立了共乘交通网络，分析了共乘出行对城市交通网络的影响以及共乘出行的流量变化。通过共乘匹配约束描述了共乘交通流量之间的相互制约关系，基于Logit选择模型探究了用户对出行费用感知的随机性。通过弹性需求描述了出行费用对出行需求的影响，建立了弹性需求的Logit随机共乘用户均衡的变分不等式模型，并严格证明了该模型的解的等价性、存在性和唯一性。在此基础上，设计了自适应并行投影算法，降低了求解大规模交通分配问题的内存需求和计算时间，求解了所提出模型并得到了全局最优解。通过2个算例验证了所提出模型和算法的有效性，结合敏感性分析得出了影响出行需求和平均出行时间的因素，最后用大规模网络验证了算法的计算可行性。

作者贡献声明：

马 捷：方案设计，论文撰写，基金支持。

李 锐：方案设计，论文修改，稿件校对。

王 华：方案设计，论文修改，稿件校对。