高性能钢梁的整体稳定性

强旭红，赵波森，姜 旭，徐 晗

（1. 同济大学土木工程学院，上海 200092；2. 浙江中天恒筑钢构有限公司，浙江杭州 310000）

高性能钢（HPS）是一种综合优化了材料力学性能，可用于低温和腐蚀环境，具备较高性价比的结构用钢，其在强度、耐火性能、可焊性和抗脆断性能等方面都比传统钢材有明显改善。作为高性能钢的一种，高强钢在科研领域得到了较高的重视，相关科研成果丰硕。

在材性方面，朱希［1］和Shi等［2］对46组高强钢进行了拉伸试验，提出了不同情况下高强钢抗力分项系数和设计强度的建议值。此外，施刚等［3］对Q460、Q690 等高强钢建立了静力拉伸条件下修正的多折线本构关系模型和以Ramberg-Osgood 模型为基础的非线性本构关系模型。在受弯构件方面，众多学者研究了其抗弯承载力、局部稳定性和整体稳定性，并将研究成果与各国规范进行了比校。Beg 等［4］对10个Nionicral70高性能钢（屈服强度为700 MPa）焊接工字形钢梁进行了四点弯曲试验和数值模拟研究，分析了翼缘宽厚比和腹板高厚比对受弯梁承载力和局部稳定性的影响，并给出了计算公式。高磊等［5］对高强钢薄壁箱形截面梁的稳定性进行了研究，分析了长细比、翼缘宽厚比和截面边长比对梁稳定性的影响，并在考虑了高强钢薄壁箱形截面梁局部和整体屈曲的基础上，提出了适用于高强钢薄壁箱形截面梁的极限承载力计算公式。Ma 等［6］对25个700 MPa、900 MPa 和1 100 MPa 级圆形、矩形和方形空心截面高强钢冷弯管状梁进行了四点受弯试验，发现现行规范（欧洲、澳大利亚、美国）对高强钢抗弯承载力的计算大多偏保守。Wang 等［7］对22 个S460 和S690 高强钢方形和矩形空心截面梁进行了三点受弯和四点受弯试验，结果表明欧洲规范（EC3）的截面分类限值对高强钢内部受压板件并不适用。Shi 等［8］对2 个Q460和3个Q890高强钢工字形截面梁在均匀受弯条件下的局部稳定性进行了试验研究和有限元分析，有限元模拟结果与试验结果的失稳形态吻合，进一步分析发现局部屈曲应力和极限应力都随着板件宽厚比的增加而降低，与中国规范（GB 50017―2003）、美国规范（ANSI/AISC 360-10）和欧洲规范（EC3）的对比结果表明，现行规范对高强钢并不适用。Elkawas 等［9］对用于桥梁工程的高强钢波纹腹板梁的整体稳定承载力进行了数值研究，并提出了针对欧洲规范（EC3）［10］的修正模型。

目前，屈服强度超过420 MPa 的高性能钢尚未纳入我国《公路钢结构桥梁设计规范》（JTG D64―2015）［11］，我国行业标准《高强钢结构设计标准》（JGJ/T 483―2020）［12］中也未给出跨中一点和1/4跨度两点加载模式下的高强钢梁整体稳定系数计算方法，而且针对已有的国产高性能钢梁的整体稳定性研究较少，普适性的评判体系和计算方法尚未完善。因此，设计了不同跨径、不同材料和不同加载方式下的受弯构件整体稳定性试验，并建立了有限元模型，对国产Q460 和Q500 高性能钢梁的整体稳定性进行了理论和试验研究。

1 Q460和Q500高性能钢梁整体稳定性试验

设计了6 根包钢产Q460 和Q500 高性能钢梁试件，并对不同对照组的试验结果进行分析。根据常规力学性能试验结果，Q460高性能钢的名义屈服强度fy为587 MPa，极限抗拉强度fu为669 MPa，Q500高性能钢的名义屈服强度fy为641 MPa，极限抗拉强度fu为694 MPa；结合延伸率统计数据，对于Q460高性能钢屈服应变εy取2.85×10−3，极限应变εu取0.19，对 于Q500 高 性 能 钢 屈 服 应 变εy取3.25×10−3，极限应变εu取0.2；Q460 与Q500 高性能钢的弹性模量E、密度ρ和泊松比ν相同，分别为2.06×105MPa、7.85 g·cm−3、0.3。

1.1 双轴对称工字形截面简支梁整体稳定弹性临界弯矩理论

如图1 所示，双轴对称工字形截面简支梁承受横向荷载时的弹性临界弯矩

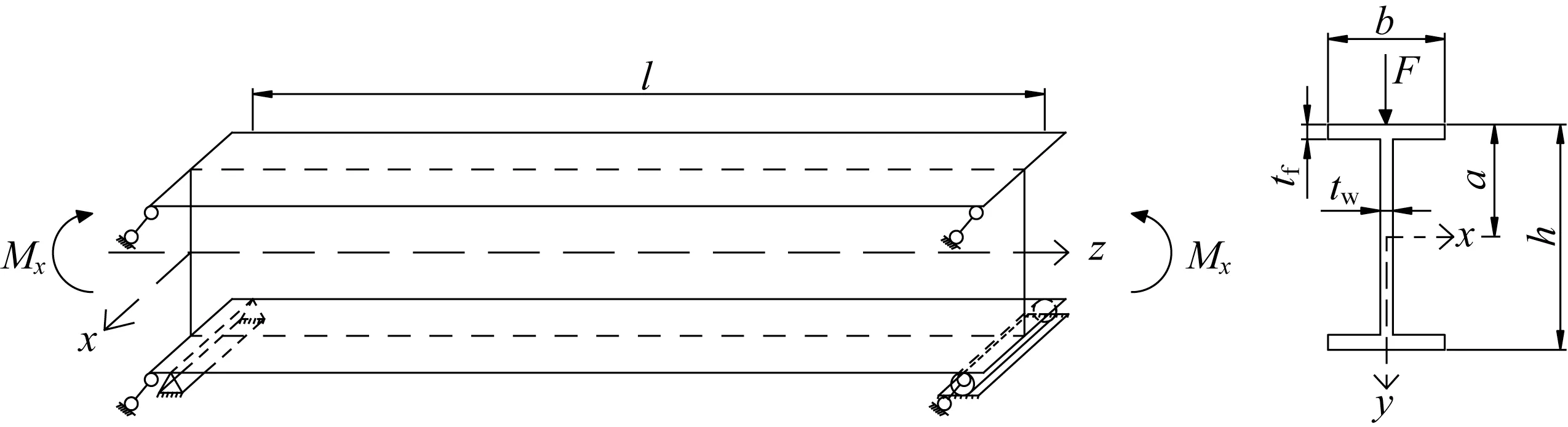
图1 纯弯曲下的双轴对称工字形截面简支梁Fig.1 Simply-supported beam with biaxial symmetrical I-shaped cross-section under pure bending

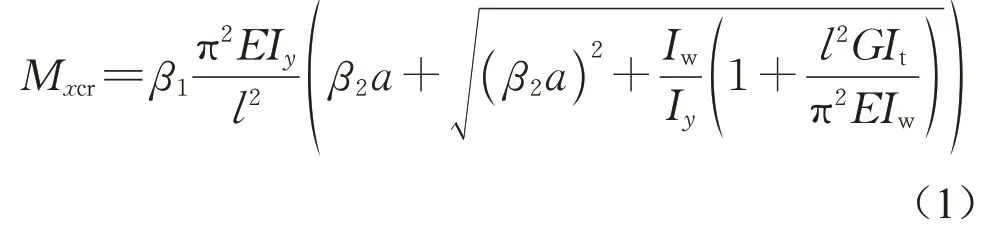
式中：β1为与荷载类型有关的系数，两点对称加载对应的β1由文献［13］中公式计算得到；β2为与荷载类型和荷载作用位置有关的系数，两点对称加载对应的β2由文献［13］中公式（简支梁侧扭屈曲临界弯矩公式中的系数如表1 所示）计算得到；Iy为截面对主轴y的惯性矩；Iw为截面扇性惯性矩；It为截面抗扭惯性矩；E为材料弹性模量；G为材料剪切模量，G=E/2(1+ν)，其中ν为材料泊松比；a为横向荷载作用点至截面剪切中心的距离。当荷载作用点在剪切中心以上时，a取负值；当荷载作用点在剪切中心以下时，a取正值。对于双轴对称工字形截面，剪切中心在截面形心处。

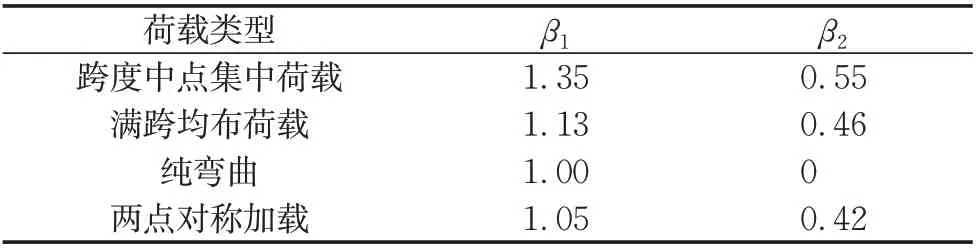
表1 简支梁侧扭屈曲临界弯矩公式中的系数［15］Tab.1 Coefficients in the formula for the lateral torsional buckling critical moment of simplysupported beams[15]

1.2 试件设计

当受弯构件的自由长度（能有效阻止侧向变形的支承点间距离，对于跨间无侧向支承点的简支梁为其跨度）小于某一临界值时，可以不考虑构件的整体稳定性［14］。文献［15］中给出了可不计算构件整体稳定性的工字形截面简支梁受压翼缘自由长度l1与其宽度b1之比的最大值，如表2 所示。对于本试验设计的简支梁试件，l1=l，b1=b。

表2 工字形截面简支梁不需要计算整体稳定性的最大l1/b1值［15］Tab.2 Maximum l1/b1 value of simply-supported Ishaped beam without calculating overall stability［15］

《公路钢结构桥梁设计规范》（JTG D64―2015）［11］也给出了l1/b1的最大值，如表3所示。

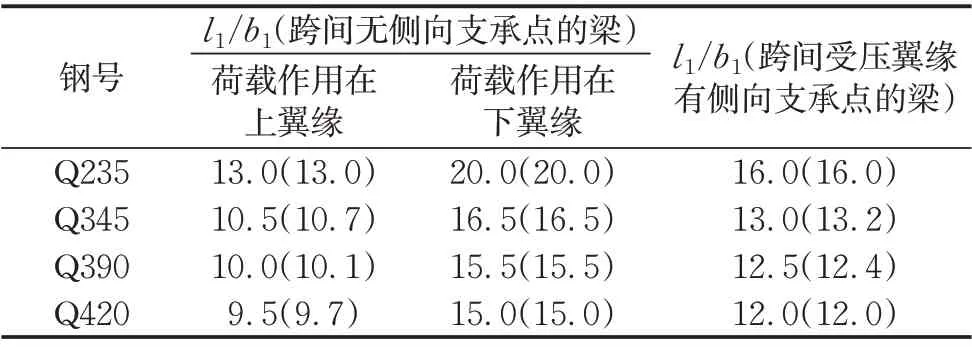
表3 工字形截面简支梁不需要计算整体稳定性的最大l1/b1值［11］Tab.3 Maximum l1/b1 value of simply-supported Ishaped beam without calculating overall stability［11］

由于按H 型钢设计无需验算局部稳定性，因此按H 型钢HN400 mm×200 mm×8 mm×13 mm 的规格设计简支梁，试件设计如表4和图2所示。根据实际工程条件，设计Q460高性能钢简支梁和杂交梁（翼缘为Q500 高性能钢，腹板为Q460 高性能钢）作为试验试件。对于Q460 高性能钢简支梁，设计2 m和4 m 跨度的对照组（分别对应不发生整体失稳和发生整体失稳，每组再设计一点加载和两点加载2种荷载类型作为对比）；对于杂交梁（翼缘为Q500高性能钢，腹板为Q460高性能钢），设计2 m跨度一点加载和两点加载作为对比，共6 根简支梁。相比截面的高度和宽度，试件梁的翼缘和腹板厚度较大，截面刚度也很大，并且在两端支座处腹板上采用与翼缘同厚度的一对加劲肋以增大截面的扭转刚度，保证试件支座处在弹性阶段不发生绕纵轴的扭转变形。

表4 高性能钢梁整体稳定性试验试件Tab.4 Specimens of overall stability test for high-performance steel beams

图2 试验加载方式（单位：mm）Fig.2 Loading mode of the test（unit：mm）

1.3 试验方案

对于每一根简支梁，不论跨度和加载类型，都采用相同的应变片和位移计布置方案。水平位移计（H1～H5）和竖向位移计（V1～V5）各5个；应变片（S1～S27）共27个，布置在跨中和l/4跨的3个截面处，如图3所示。为保证试验条件为静力加载，4 m跨Q460简支梁一点加载和两点加载的加载速率为2 kN·s−1，每加100 kN，持力1 min；其余4根梁加载速率为3 kN·s−1，每加200 kN，持力1 min。数据采集频率为次·s−1。为模拟集中力加载，在加载处放置一块宽度为90 mm的钢块。

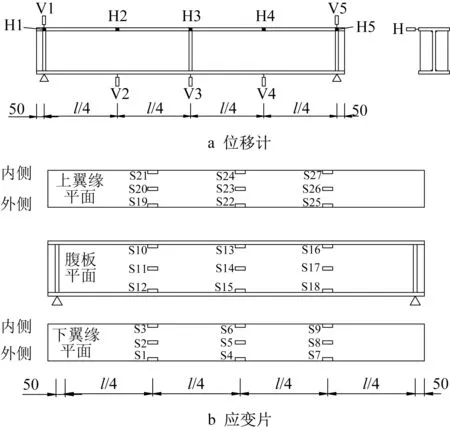
图3 位移计和应变片布置（单位：mm）Fig.3 Layout of displacement gauge and strain gauge（unit：mm）

1.4 试验加载

针对不同跨度的钢梁，根据实验室现有条件，选择不同的实验设备进行加载。各试件在完成应变片和位移计安装后的加载过程如图4所示。

图4 试件加载Fig.4 Loading of specimens

试件1、5加载后期，跨中上翼缘、加劲肋发生明显的屈服变形，破坏时跨中向一侧倾斜，破坏荷载分别为1 970 kN 和3 460 kN。试件2、6 破坏时弯剪区腹板局部屈曲，破坏荷载分别为2 825 kN 和4 402 kN（2 个F的总和）。试件3 破坏时靠近梁跨中处发生侧倾，梁整体失稳，破坏荷载为940 kN。试件4破坏时梁纯弯曲段侧倾，发生整体失稳，破坏荷载1 693 kN（2个F的总和）。

1.5 位移-荷载和应变-荷载曲线

各试件的位移-荷载和应变-荷载曲线如图5～7所示。

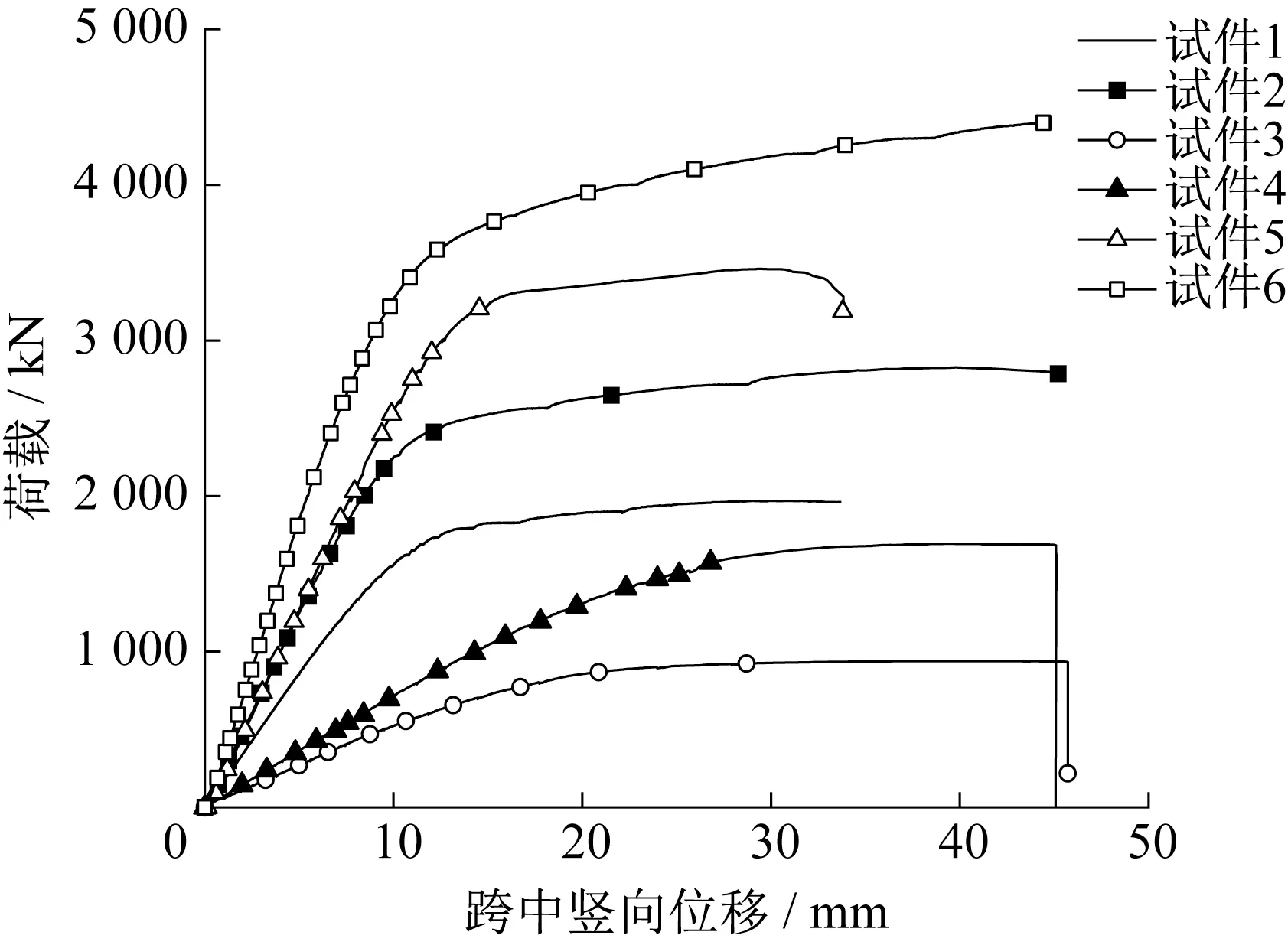
图5 跨中竖向位移-荷载曲线Fig.5 Midspan vertical displacement-load curve

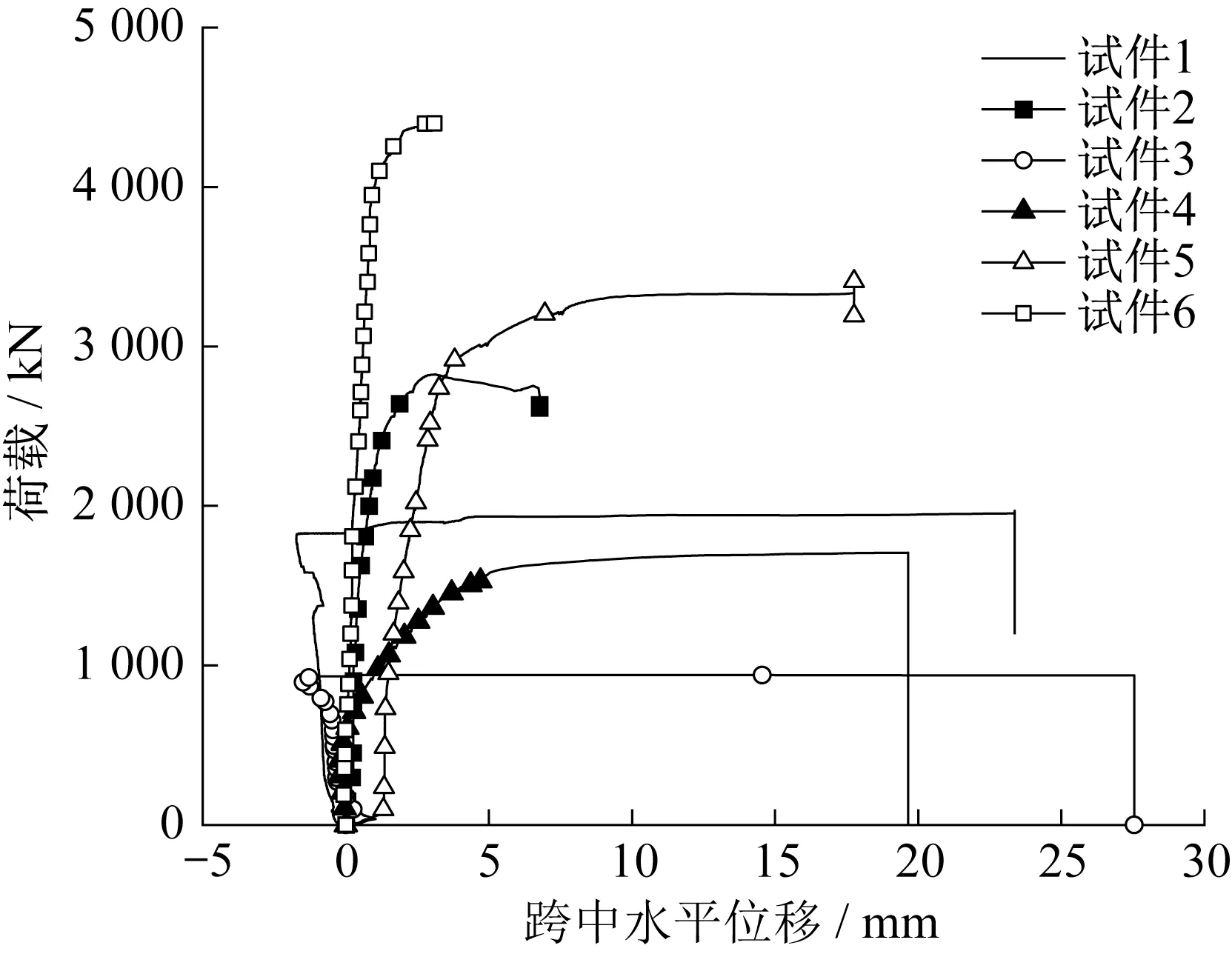
图6 跨中水平位移-荷载曲线Fig.6 Midspan horizontal displacement-load curve

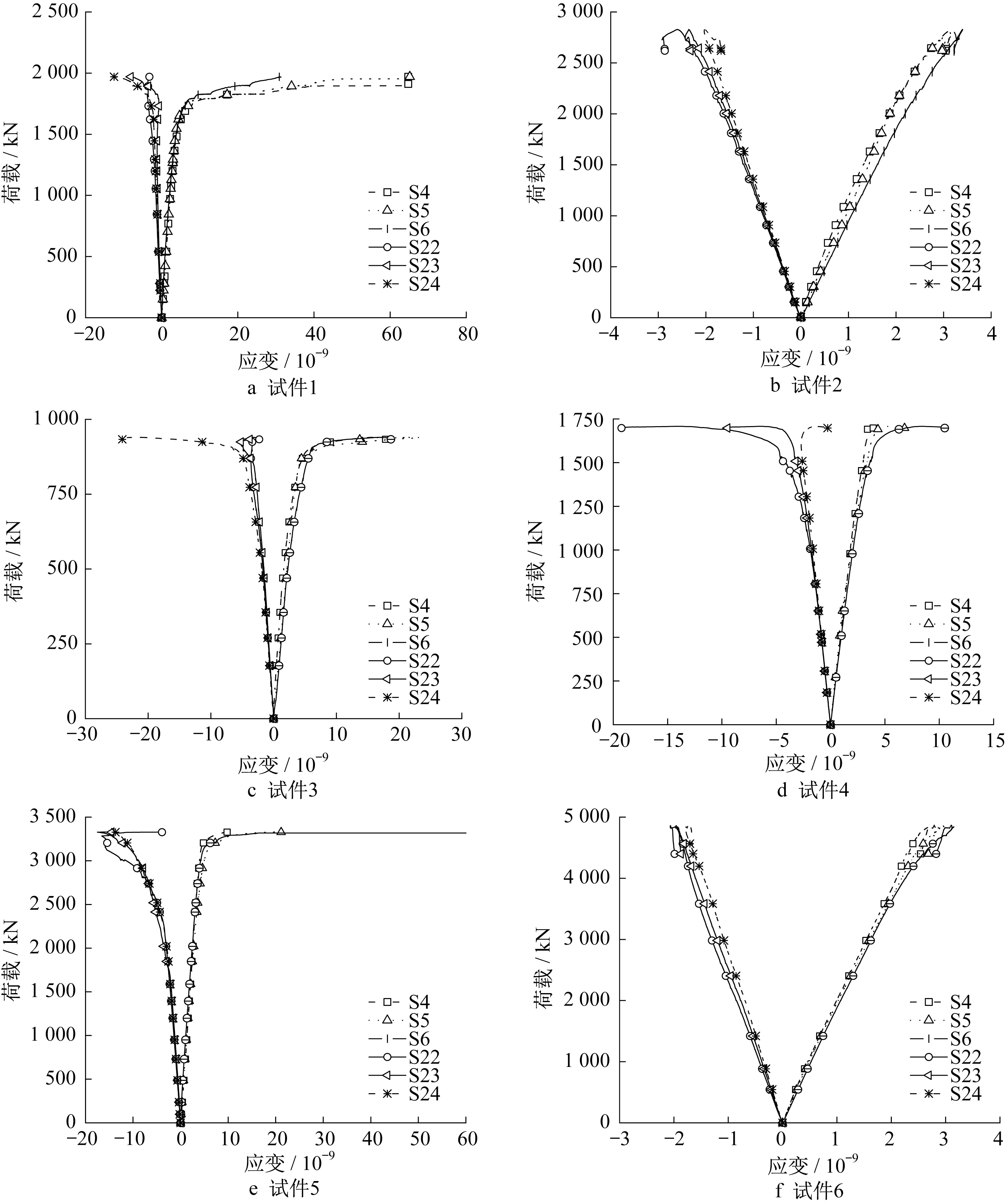
图7 应变-荷载曲线Fig.7 Strain-load curve

从图5可以看出，试件1～6的跨中竖向位移-荷载曲线先线性增长，接近极限荷载后进入非线性阶段，荷载增长缓慢，位移增长加快，在受弯时能够较好地发挥材料塑性。图6 中试件1、3、4、5 的水平位移均在荷载不再增大时剧烈增加，说明其在平面外的弯曲和扭转发展未受到抑制，从而使试件发生破坏。然而，这并不意味着4 个试件的破坏模式均为整体失稳。从试验破坏后形态和有限元模拟结果（见图11）来看，试件1和试件5侧向位移后期剧烈增大的原因是：试验过程中荷载加载的偏心或试件初始缺陷在较大的集中荷载作用下使加劲肋一侧发生局部屈曲，而一侧屈曲的加劲肋致使加载偏离预期轨道，偏心距突然增大，导致侧向位移剧增，因此试件1和试件5的破坏模式并非整体失稳，而是强度破坏；试件3和试件4发生受弯整体失稳破坏。在加载过程中试件2 和试件6 侧向位移均较小。对于试件2，荷载减小侧向位移增大阶段的产生是由未及时暂停加载而导致的，若不计该原因造成的侧向位移，试件2、6的侧向位移则均在5 mm内，并且增长过程较为线性。虽然由表7 可知试件2、6 的实际破坏荷载小于弹性极限荷载，但是由式（2）、（3）计算得到在距支座l/4 处最危险点的Mises 应力大于Q460 屈服极限，因此可以判定试件2、6 破坏模式为截面强度破坏。综上，试件破坏模式符合设计预期。

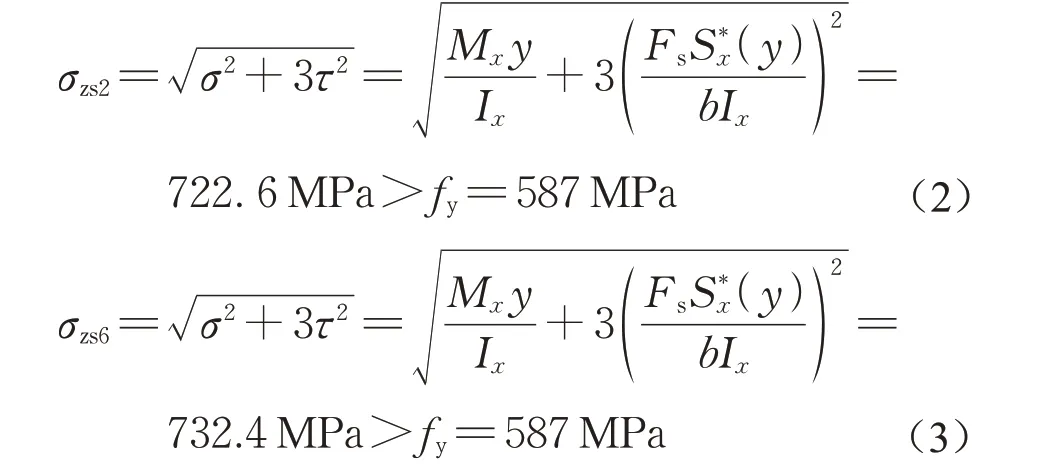
式中：σzs2、σzs6分别为试件2 和试件6 距支座l/4 处最危险点的Mises 应力；σ、τ分别为正应力和切应力；Mx为绕主轴x的弯矩；y为最危险点相对x轴的距离；Fs为最危险点处截面的剪力；S*x(y)为最危险点处截面面积矩；Ix为截面对主轴x的惯性矩。

2 Q460和Q500高性能钢梁整体稳定性有限元分析

采用通用有限元软件Abaqus对第1节的6根试验梁建立有限元模型，考虑材料和几何双非线性。将有限元模拟结果与试验结果进行对比，验证模型的有效性和准确性。然后，将模拟结果与弹性极限荷载、塑性极限荷载、弹性临界荷载、试验结果以及《钢结构设计标准》（GB 50017―2017）［16］中整体稳定系数计算进行比较，判定模拟结果的合理性和《钢结构设计标准》［16］对高性能钢的适用性。

2.1 有限元模型

2.1.1 材性输入

对于单调荷载作用下的高强度结构钢，采用无屈服平台的多折线本构模型［3］，如图8所示。图8中，fu为极限抗拉强度，εy为屈服应变，εu为极限应变。材性输入时输入多折线模型曲线上的2个关键点（εy，fy）和（εu，fu），已在第1节首段中给出了具体数值。

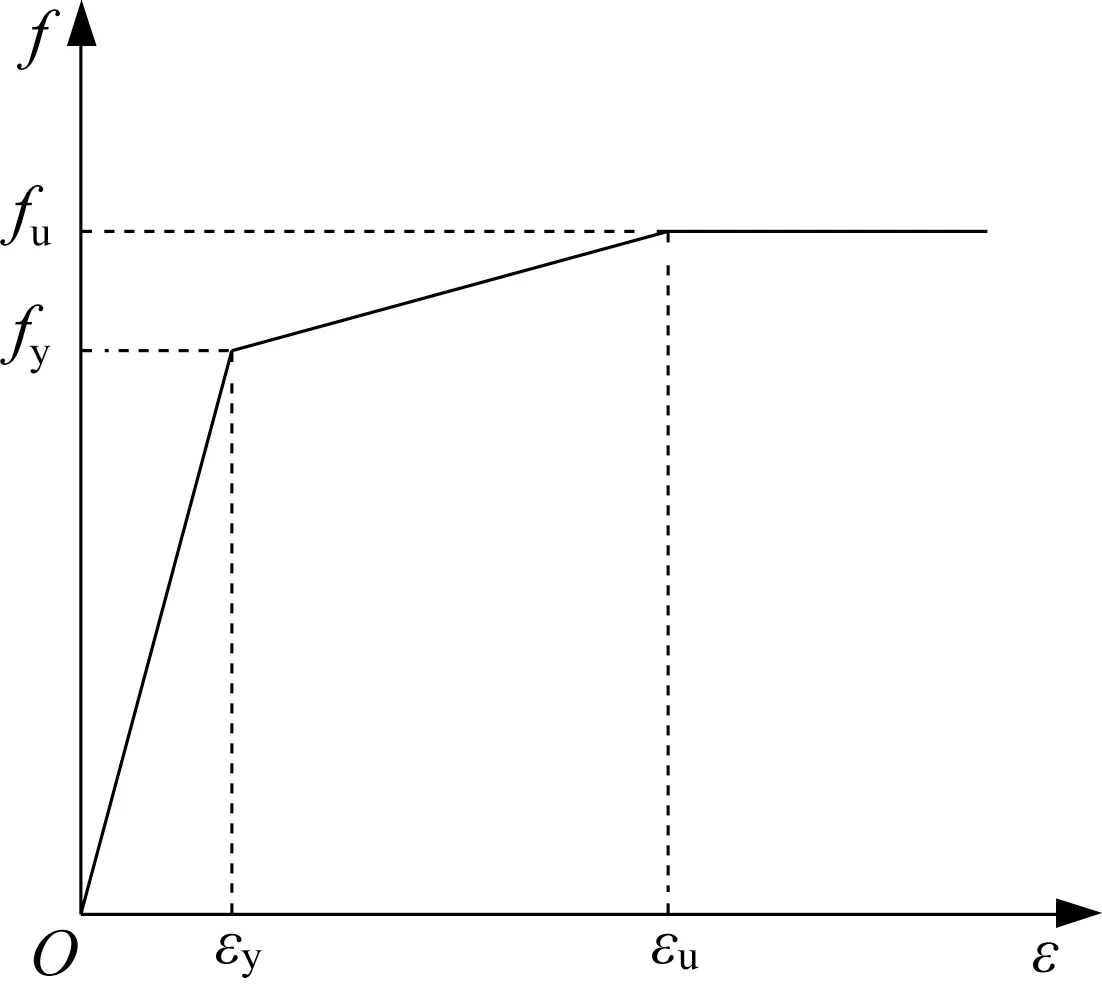
图8 无屈服平台的应力-应变多折线模型［3］Fig.8 Multi-line model of stress-strain relationship without yielding platform［3］

2.1.2 几何模型和网格划分

采用通用有限元软件Abaqus 对6 根梁建模，几何模型按设计尺寸建模，板件之间实际为焊缝连接，为简化模型建模时不考虑焊缝。以2 m跨一点和两点加载简支梁（Q460高性能钢）为例，几何模型如图9所示。

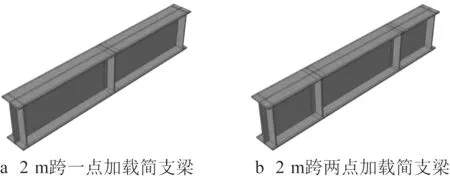
图9 梁的几何模型（Q460高性能钢）Fig.9 Geometric model of beams （Q460 highperformance steel）

2.1.3 荷载和边界条件设置

有限元模型建立时，在两端支座加劲肋的底部约束梁高方向和梁侧向的平移，并在其中一端的支座中心处约束梁跨度方向的平移，防止梁形成机构。试验中，在施加集中力处放置宽度为90 mm（2 m 跨Q460 一点加载简支梁放置宽度是60 mm）的钢块，液压加载装置的力施加到钢块上以模拟集中力，所以有限元模拟时在施加集中力处设置面与面形心点的Kinematic 耦合，在面形心点施加集中力，以精准模拟试验时的荷载条件。以2 m跨一点和两点加载简支梁（Q460高性能钢）为例，荷载和边界条件设置如图10所示。

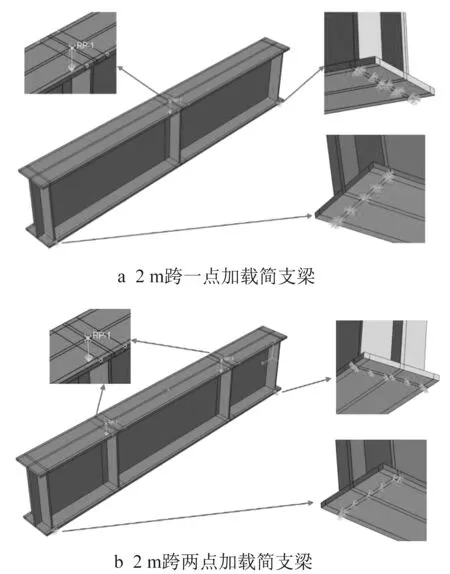
图10 梁的荷载和边界条件（Q460高性能钢）Fig.10 Loading and boundary conditions of beams（Q460 high-performance steel）

2.1.4 分析方法和过程

在数值模拟中，为了追踪结构的后屈曲响应，使用弧长法对试件的加载过程进行分析。试件在制造和搬运等过程中会产生初始缺陷，在弧长法分析前首先进行特征值屈曲分析，以得到目标屈曲形态；然后，将目标屈曲形态的节点位移进行缩放后加到初始有限元模型上，以模拟初始几何缺陷（不考虑荷载偏心）；最后，采用弧长法在大变形情况下进行几何非线性分析。各试件添加初始缺陷时的参数如表5所示，模态1、模态2是指试件的第1阶、第2阶屈曲模态。

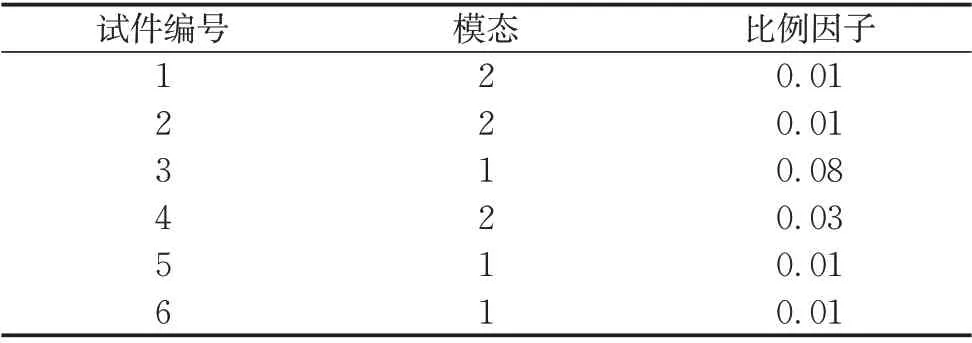
表5 试件初始缺陷参数Tab.5 Initial defect parameters of specimens

2.2 与试验结果对比

6根梁试验与有限元模型破坏形态、跨中下翼缘竖向位移对比分别如图11、12所示。

图11 试验和有限元分析得到的破坏形态Fig.11 Failure mode obtained from tests and finite element analysis

由图12 可知，试件1～6 的跨中竖向位移-荷载曲线的试验结果与有限元模拟结果均吻合较好。由表6 可知，试验与有限元分析得到的极限荷载误差在3%以内，并且由图11发现，有限元模型的破坏形态与试验的十分相近，从而验证了该有限元模型的有效性。

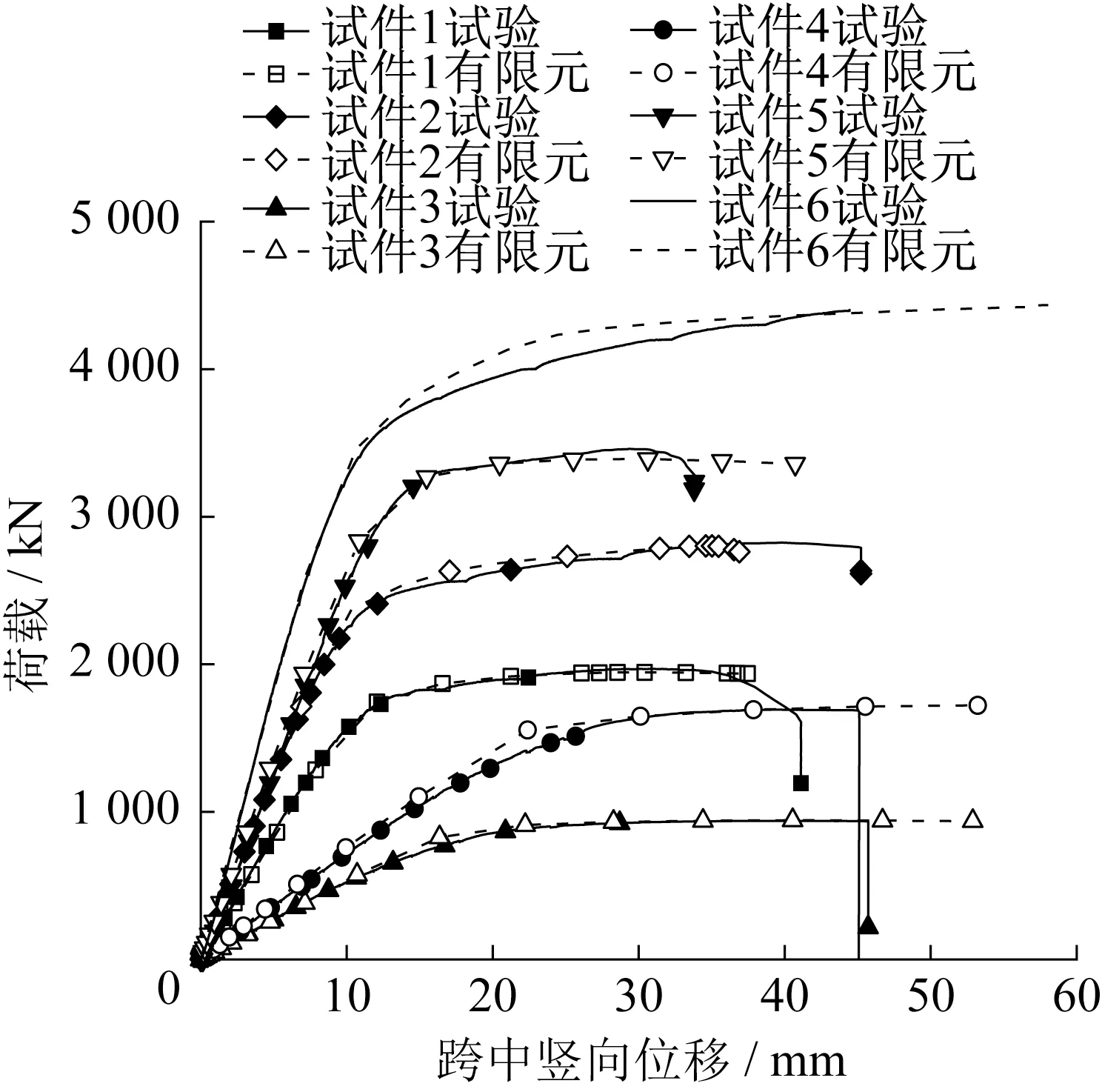
图12 试验和有限元分析得到的跨中竖向位移-荷载曲线Fig.12 Midspan vertical displacement-load curve obtained from tests and finite element analysis

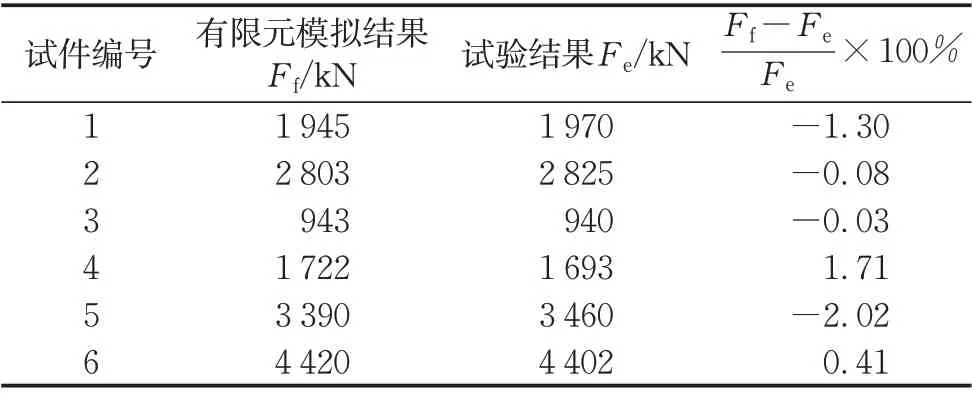
表6 试验与有限元分析得到的极限荷载对比Tab.6 Comparison of ultimate loads obtained from tests and finite element analysis

2.3 结果分析与规范校验

当梁的弹性状态即将结束时，相应的弹性极限弯矩

式中：Wx为梁的弹性截面模量。

梁截面形成“塑性铰”，相应的塑性极限弯矩

式中：Wpx为梁的塑性截面模量。

利用式（1）、（4）、（5）和《钢结构设计标准》（GB 50017―2017）［16］中第6.2 节和附录C 的内容分别计算双轴对称工字形截面简支梁承受横向荷载时的弹性临界弯矩、弹性极限弯矩、塑性极限弯矩和受弯整体稳定系数φb，再将弯矩转换为各试件在加载模式下对应的集中力，如表7所示。

表7 极限荷载对比Tab.7 Comparison of ultimate loads

由表7 可知，除试件2、6 外，无论强度破坏还是整体失稳，破坏荷载都大于弹性极限荷载甚至塑性极限荷载，进一步说明了Q460、Q500高性能钢具有较好的塑性性能。试件2、6因过于密集的加劲肋而使应力集中在支座附近的腹板区域，使得腹板先达到极限强度，发生强度破坏，所以其试验值不能与理论值进行充分对比。

同时观察弹性临界荷载，对于短跨的试件1、2、5、6，其取值远超弹性极限荷载和塑性极限荷载，这是由于假设材料始终处于弹性状态，因此仅适用于临界应力不超过比例极限时的情形。试件3、4的弹性临界荷载小于弹性极限荷载，这是因为试件3、4跨度大，在弹性临界荷载的计算过程中，材料始终保持弹性状态。

相对于弹性临界荷载，《钢结构设计标准》（GB 50017―2017）［16］中采用弹塑性方法对失稳临界荷载进行修正，因此按照该方法计算得到的受弯整体稳定系数φb对短跨梁仍适用。对于试件1、5，由《钢结构设计标准》（GB 50017―2017）［16］计算得到的整体稳定临界荷载不会出现临界荷载数倍于弹性极限荷载和塑性极限荷载的情况，相对于真实破坏荷载保留20.8%、15.1%的安全余量。

由《钢结构设计标准》（GB 50017―2017）［16］计算得到的φb可知，试件3、4的破坏模式为整体失稳，相对于真实破坏荷载也保留31.9%、26.3%的安全余量。

综上，《钢结构设计标准》（GB 50017―2017）［16］对于Q460、Q500 高性能钢的整体稳定性仍具有较好的适用性，但不同跨径下安全余量有较大的波动。

根据表2，分别计算采用Q460、Q500 高性能钢试件在无需计算整体稳定性时的最大l1/b1值，如表8所示。

表8 规范和试验得出的不需要计算整体稳定性的最大l1/b1值Tab.8 Maximum l1/b1 value without calculating overall stability obtained from the Standard and tests

由表8 可知，无需计算整体稳定性时杂交梁的最大l1/b1值与Q460钢梁的一致。对于要求钢结构只发生强度破坏的设计，将Q460钢梁的翼缘转换为相同尺寸的Q500钢板，试件不会发生整体失稳。由于钢梁是结构的主要受弯构件，工字形截面钢梁的抗弯承载力绝大部分由翼缘承担，因此仅将翼缘由Q460 高性能钢改用Q500 高性能钢，可在很大程度上提高构件的抗弯承载力。由本试验得出的无需计算整体稳定性的最大l1/b1值略大于文献［15］给出的理论值，说明文献［15］关于整体稳定性的规定适用于Q460 和Q500 高性能钢，并且具有一定的安全冗余度。本试验中l1/b1为19.5 的试件3、4 的破坏模式为整体失稳，也与文献［15］的预期结果吻合。因此，本试验中梁的整体稳定性计算满足文献［15］给出的最大l1/b1的要求，可为《公路钢结构桥梁设计规范》（JTG D64―2015）［11］相应规定的适用范围扩展至Q460 和Q500 高性能钢提供试验与理论依据。

3 结论

（1）对于不发生整体失稳的短跨梁而言，在保证加载不偏心的情况下，翼缘采用比腹板更高强度钢的杂交梁能够最大限度地发挥材料的力学性能。

（2）《公路钢结构桥梁设计规范》（JTG D64―2015）［11］中，对于工字形截面简支梁，在无需计算整体稳定性时，最大l1/b1值的适用范围可扩展至Q460、Q500高性能钢及其杂交梁。

（3）《钢结构设计标准》（GB 50017―2017）［16］中受弯构件整体稳定系数计算对Q460、Q500 高性能钢及其杂交梁有较好的适用性，但需改进以保证不同跨径、不同加载方式下梁的安全冗余度，减小整体稳定系数随跨径和加载方式的波动。

（4）对于建立的简支梁有限元模型，计算结果与试验结果比较吻合，验证了有限元模型的有效性。

作者贡献声明：

强旭红：项目构思和试验设计，试验结果分析，论文修改。

赵波森：试验执行，数据分析，论文初稿写作与修改。

姜 旭：参与试验研究，试验结果分析，论文修改。

徐 晗：参与试验研究，试验结果分析，论文修改。