基于混沌-广义回归神经网络的矿井涌水量预测

李建林，高培强，王心义，赵帅鹏

(1.河南理工大学 资源环境学院，河南 焦作 454000；2.煤炭安全生产与清洁高效利用省部共建协同创新中心，河南 焦作 454000)

0 引 言

矿井涌水量是指在单位时间内，矿山建设和生产过程中涌入井巷中的总水量。准确预测涌水量对于矿山安全生产具有重要作用[1]。地表水体(大气降水、河流等)、开采条件(开采深度和规模、煤层围岩出露条件、上覆地层透水性等)、地质构造等因素都会对矿井涌水造成直接或间接的影响。学者们针对矿井涌水量的预测从确定性方法逐渐发展到非确定性随机预测，研究方法不断更新[2-4]。但受水文地质条件复杂性的影响，确定性方法(解析法、水均衡法等)的计算结果往往会出现较大误差[5]；非确定性随机预测方法(水文地质比拟法、模糊数学模型、灰色系统理论、BP 神经网络等)主要受限于实测资料的积累程度，而且这类方法对开采条件下矿井充水因素的动态变化考虑不够[6]。整体而言，目前涌水量预测存在的主要问题是对影响涌水量的因素认识不够、不能找出起决定作用的因素；或已找到起决定作用的因素，但这些因素的资料不全或数据难以获取，导致建模及预测过程简化。

混沌理论(Chaos Theory)可以让时间序列中隐藏的丰富的动力学信息得以恢复[7]，是研究复杂系统的有效工具。我国将其应用到矿井涌水量预测的研究始于1996 年，经过20多年的发展，取得了一定的成果[8-10]：①很多矿井的涌水量时间序列具有混沌特性；这在理论和实践中都得到了验证；②利用全域法、局域法、加权一阶局域法等进行涌水量短期预测，取得了较好结果。但与混沌理论在其他领域的研究相比，进展较为缓慢。直到2016年，才有学者将混沌理论与BP神经网络相结合，建立了新的涌水量预测模型[11]。目前，基于混沌理论的涌水量预测的研究成果仅能实现对涌水量的短期预测，对煤矿安全生产和矿井水资源的利用意义不大。

人工神经网络(ANN)在时间序列模拟与预测上具有独特的优势。广义回归神经网络(GRNN)是一种径向基神经网络，它具有模型结构简单、调整参数少，学习速度快和预测准确性高的优点，适用于解决非线性问题。王雪冬等[12]将涌水量的3个主要影响因素作为输入神经元，建立了GRNN的涌水量预测模型，预测效果较好。利用GRNN进行涌水量预测时，输入层神经元的个数及其取值(即涌水影响因素的选择及其取值)是决定模型精度的关键。而往往有些影响因素的数据难以量化，或在众多影响因素中难以确定起关键作用的因素，导致GRNN模型具有较大的主观性和局限性。

混沌理论认为，一维的时间序列中蕴藏着大量的多维的相关因素的信息，而相关因素的个数和取值可通过相空间重构获得[13]。鉴于此，本研究将混沌理论与GRNN结合在一起，利用涌水量时间序列相空间重构来确定GRNN输入层神经元的个数及其取值(减少单一GRNN模型的主观性和局限性)，建立混沌-广义回归神经网络(Chaos-GRNN)模型，以实现对矿井涌水量更有效的预测。

1 Chaos-GRNN预测模型研究方法

1.1 相空间重构

相空间重构中，延迟时间τ和嵌入维数m选取十分关键。采用自相关函数法确定延迟时间τ。与复自相关法、重构展开法和互信息量法相比，该方法具有对时间序列要求低、计算简单的优势[14]；采用Cao方法确定嵌入维数m，该方法具有主观参数少(仅有1个主观参数τ)、信号区分能力强、计算效率高的优点[15]。

延迟时间τ和嵌入维数m确定后，进行涌水量时间序列X={x1,x2,…,xn}的相空间重构，得到m维的向量序列Yi为

Yi={xi,xi+τ,xi+(m-1) τ}

(1)

其中：i=1,2,…,M,M=n-(m-1)τ。

1.2 最大Lyapunov指数

最大Lyapunov指数λmax为系统是否具有混沌特征的辨识参数(若λmax>0，则系统具有混沌特征)，也可以确定重构序列的预测步长T(T=1/λmax)[10]。计算λmax的方法主要有定义法、Wolf法、Jacobian法、p-范数法等；相比较而言，Wolf法运算更为简单[14]，本研究采用该方法计算λmax。

以上方法在相关文献中有详细介绍[14-15]，此处不再赘述。

1.3 广义回归神经网络

(2)

式中：d(x0,xi)=(x0-xi)T(x0-xi)/2σ2，xi、yi分别为随机变量x和y的样本观测值；n为样本容量；σ光滑因子(正态分布标准差)。

GRNN由输入层、模式层、加和层和输出层组成[18](图1)。

图1 GRNN结构

1.4 Chaos-GRNN模型

充分发挥混沌理论和GRNN各自的优势，将其有机地结合在一起，建立涌水量Chaos-GRNN预测模型，具体步骤如下：

1)计算时间序列{x1,x2,…,xn}的延迟时间τ、嵌入维数m和最大Lyapunov指数λmax。m为矿井涌水量影响因素的个数，并将其作为Chaos-GRNN模型的输入、模式层神经元的个数；输入神经元的取值由式(1)确定。T=1/λmax确定GRNN模型的预测步长。

2)将重构好的向量序列Yi分成训练数据和验证数据两类(验证数据的个数为T-1)。针对训练数据，基于Matlab神经网络工具箱，采用交叉验证的方法对newgrnn( ) 函数的最佳Spread 参数值进行寻优，得到光滑因子σ。然后，将训练好的输入层、模式层数据和优化参数相结合，构建Chaos-GRNN模型。

3)导入验证数据(Yj,Yj+1,…,Yj+T-2)，进行模型验证。导出结果为：Yj+T-1=(xj+T-1,xj+T-1+τ,…,xj+T-1+(m-1)τ)，则xj+T-1+(m-1)τ为j+T-1+(m-1)τ时刻的涌水量的预测值(验证过程须假设此时刻之前的涌水量已知)。

4)预测下一时刻的涌水量。为保持预测长度为T，在导入数据中去掉Yj，增加Yj+T-1进行模拟。由于上一时刻之前的涌水量已知，为提高预测精度，用实测涌水量代替预测值进行预测。导出结果为Yj+T=(xj+T,xj+T+τ,…,xj+T+(m-1) τ)，则xj+T+(m-1) τ为该时刻的涌水量的预测值。

5)重复步骤4)，即可得到一个时期内的涌水量预测结果。

6)预测结果用相对误差(EAP)、平均相对误差(EMAP)和精度(PP)来量化：

(3)

(4)

PP=(1-EMAP)×100%

(5)

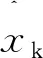
2 研究区概况及数据来源

2.1 研究区及充水水源概述

平煤十二矿位于平顶山矿区东部，主采煤层为二组煤，二1煤层底板灰岩水和采空区积水对煤矿安全生产的威胁较大；矿井正常涌水量为129 m3/h，矿井涌水量相对较小，但三水平生产以后，随着开采深度的增加和地质、构造条件的变化，矿井水害防治工作逐渐引起重视。涌水量直接来源为先期开采的采空区积水、煤层顶板砂岩水、煤层底板灰岩水，间接水源为大气降水和地表水。

2.2 涌水量数据来源及特征

根据497个月的涌水量实测数据(1976年2月至2015年12月)进行建模和验证(图2)。选取1976年2月至2012年12月涌水量数据进行时间序列的相空间重构，并确定涌水量影响因素的个数；选取2012年7月至2013年12月涌水量数据进行Chaos-GRNN建模；2014年1月至2015年12月的涌水量数据进行模型验证。

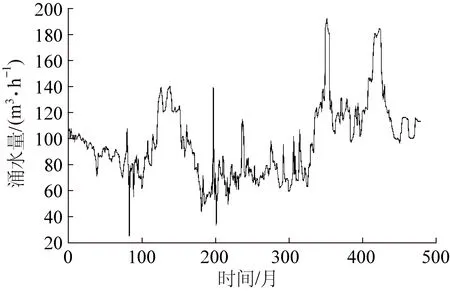
图2 平煤十二矿涌水量趋势

3 涌水量结果预测

3.1 相空间重构

利用自相关函数法求得涌水量时间序列的延迟时间τ=13个月(图3)；利用Cao方法求得其嵌入维数m=7(图4)，图4中E1(m)为嵌入维数公式中相同维数下距离变化均值的比值。利用公式(6)和式(7)计算得到Lyapunov指数λ=0.053。

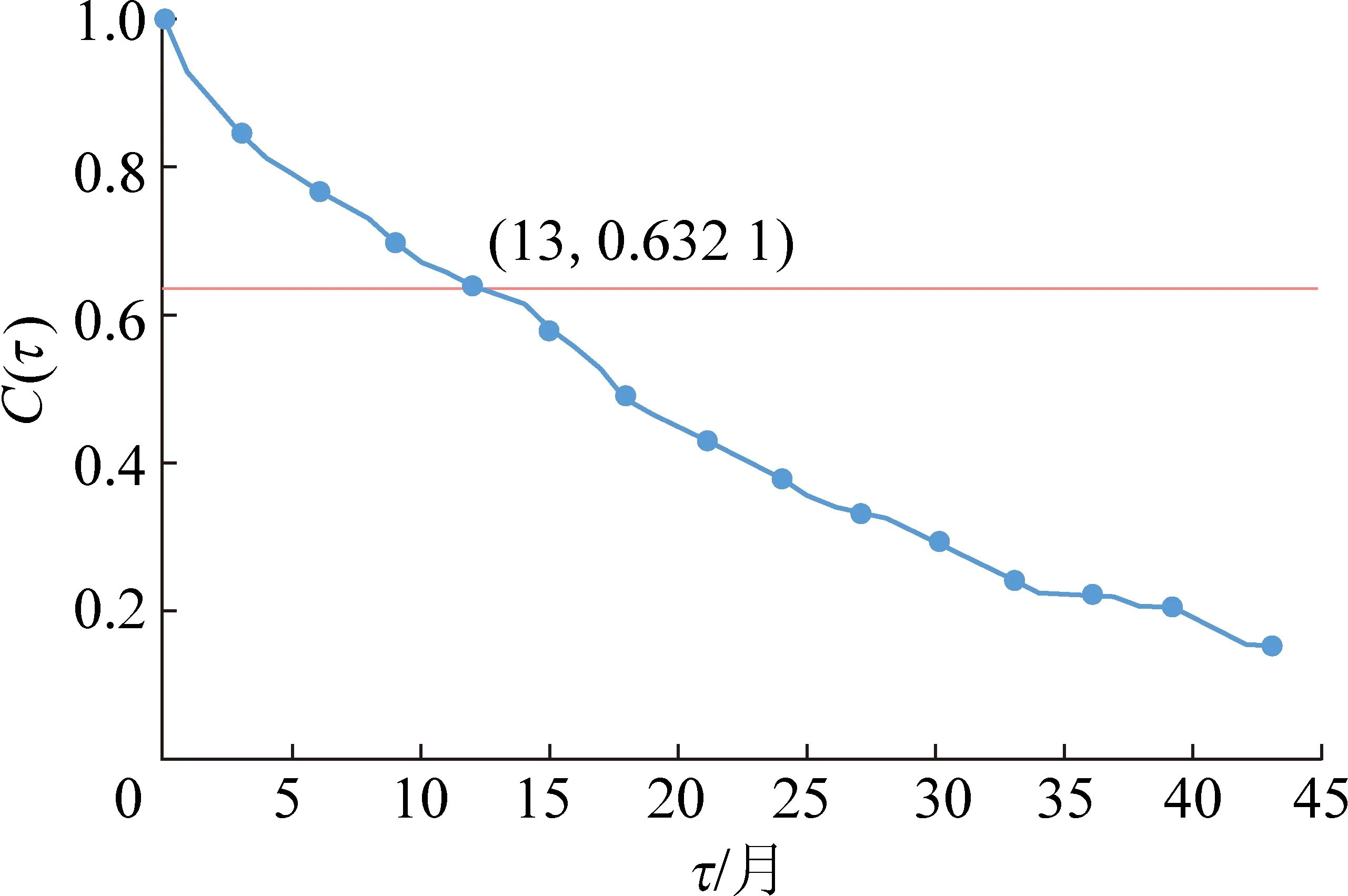
图3 延迟时间τ与自相关系数C(τ)的关系

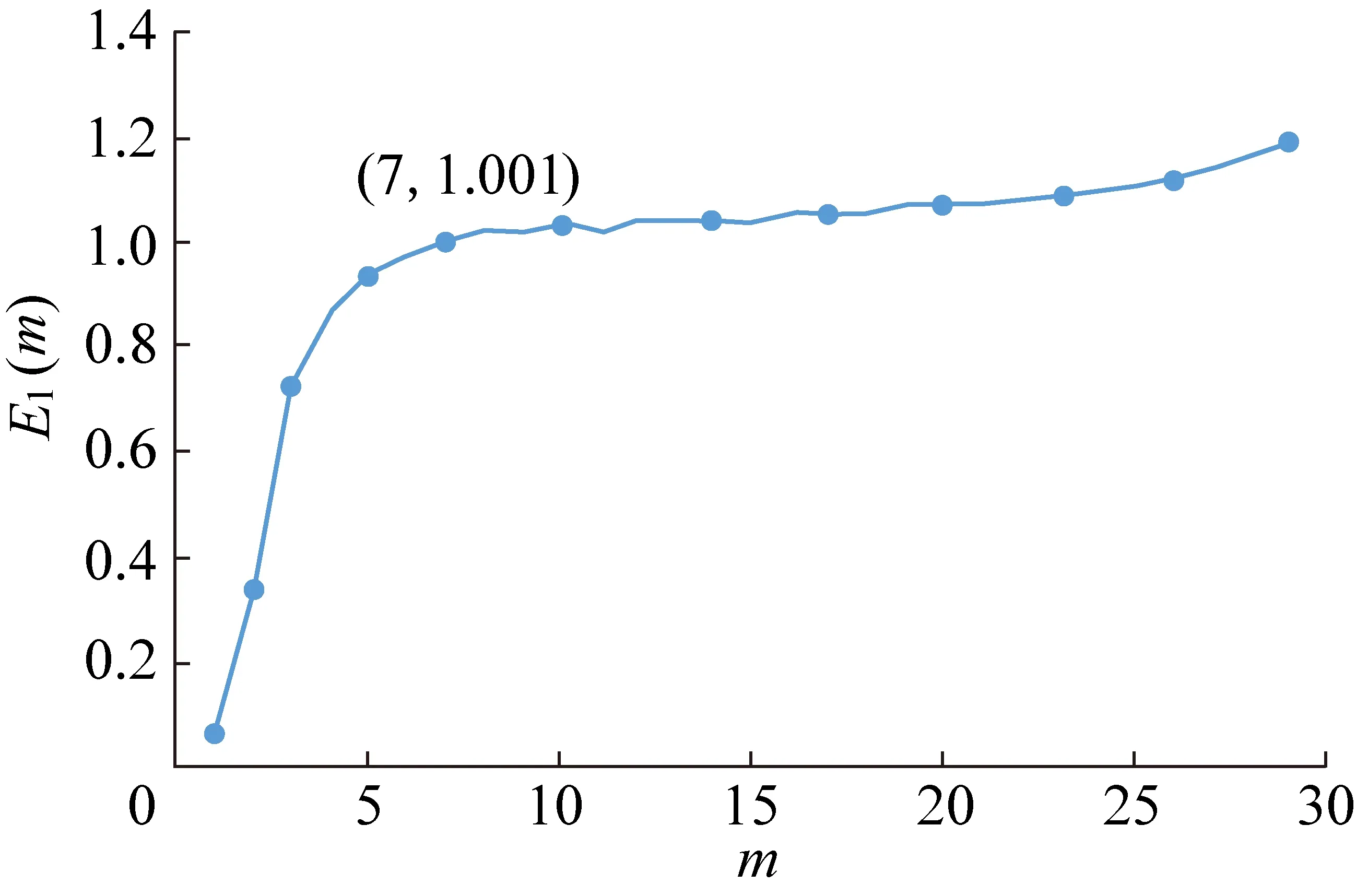
图4 嵌入维数m与E1(m)的关系

嵌入维数m=7，表示矿井涌水量影响因素为7个，以此确定Chaos-GRNN模型的输入层神经元的个数为7。λ>0，表明该时间序列具有混沌特征。T=1/λmax=18.86≈19，即Chaos-GRNN模型的预测时长为19个月。

对平煤十二矿的涌水量时间序列进行重构，得到一个时间延迟为13个月的7维向量空间Y：

(6)

要利用2014年1月至2015年12月的涌水量数据{x456,x457,…,x479}对模型进行验证，即：①x1,x2,…,x455已知，为实测涌水量；②假设x456,x457,…,x479未知，须利用所建模型预测；③在式(6)中Y378～Y401最后一列数未知，所以须选取Y378之前的向量进行训练。

3.2 涌水量预测

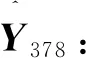
(7)

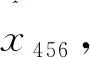
(8)

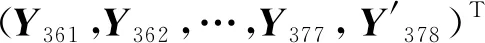
(9)

3)重复以上步骤，可得x458,x459,…,x479的预测值，即平煤十二矿2014年1月至2015年12月的矿井涌水量的预测值(表1)。

4)预测过程中，设光滑因子初值为0.1，步长为0.1，终值为2，通过循环交叉验证选定每次预测的最佳值(表1)。

利用式(3)—式(5)对预测结果进行评估。由表1可以看出，Chaos-GRNN模型预测值的最大误差为12.98%，最小误差为0.001%，平均误差为5.02%，预测精度达到了94.98%。

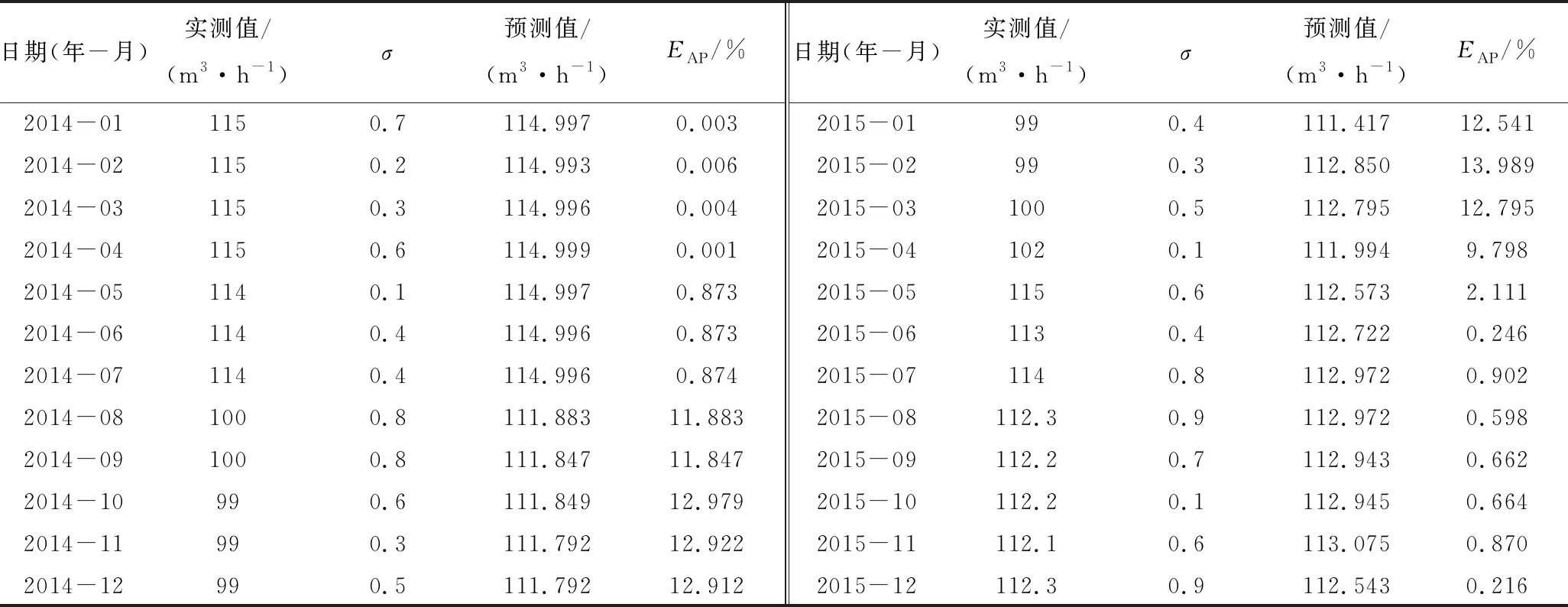
表1 Chaos-GRNN模型预测结果

4 讨 论

4.1 矿井水文系统产生混沌的机理

如果将矿井涌水作为研究主体，把矿井涌水及其各影响因素视为一个整体，则可称之为矿井水文系统。该系统具有明显的循环特征：随着开采深度和开采面积等的增加，矿井涌水量也随之增加；矿井水文系统各要素通过自身的调节以适应这种改变，逐步达到相对稳定的状态；此时，矿井水文系统完成一次演化过程。随着开采深度和开采面积等再一次改变并达到一定程度后，矿井水文系统各要素也再次随之变化，进入下一次循环(图5)。

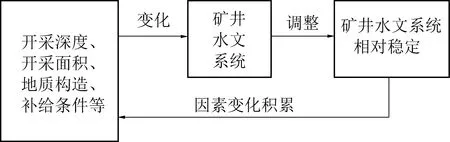
图5 矿井水文系统演化过程

该循环是在上一次循环结果的基础上进行的，所以可用迭代来描述；而迭代是系统形成混沌的主要机制。所以，矿井水文系统的演化过程具有混沌特征；演化过程的不可逆性、非平稳性和演化结果的多样性都是混沌特征的表现[9]。

4.2 混沌理论和人工神经网络的优势

目前，涌水量预测存在的主要问题是影响涌水量主控因素的资料不全或难以量化。而按照混沌理论，嵌入维数m等于矿井涌水量影响因素的个数；各影响因素的取值即为重构后相空间的列向量Yi。所以通过混沌理论可量化涌水量的主控因素。但Yi的取值依旧是涌水量，而并非各影响因素的真正取值，所以，这种量化不是完全的量化。这也导致了混沌理论的应用受阻。2013年至今，利用混沌理论进行矿井涌水量预测基本处于停滞状态。

处理数据恰好是人工神经网络(ANN)的优势：ANN通过强大的对样本的自适应、自学习功能，可以完成对输入神经元的有效输出，从而达到预测的目的；但由于ANN对涌水量影响因素选择的主观性、局限性，ANN模型也未得到广泛的重视。

因此，混沌理论与ANN有机地结合在一起(相空间重构确定输入神经元的个数、取值，及预测时长)，解决了影响因素选择的主观性、局限性问题；同时，也加深了人们对混沌理论更深入的理解，应该会对混沌理论发展和应用有所促进。

4.3 Chaos-GRNN模型的适用性

1)只要矿井水文系统具有混沌特征，理论上就可以对涌水量序列进行相空间重构，进而建立涌水量预测的Chaos-GRNN模型(图6)。由矿井水文系统产生的机理和已有的研究表明，矿井水文系统具备了成为混沌系统的条件[7-9，19-21]。

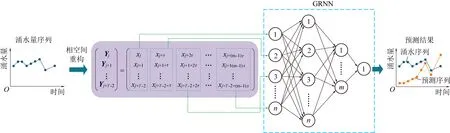
图6 Chaos-GRNN模型结构

2)在进行相空间重构和GRNN建模时，需要涌水量序列较长(至少连续3～5 a的涌水量观测值)，才能保证建模的效果；而我国生产矿井都有专门的涌水量观测和处理的部门(一般在地测科)，这些数据很容易获得。所以，Chaos-GRNN模型具有很好的适用性。

3)目前，判断一个复杂系统是否具有混沌特征，常用的方法是最大Lyapunov指数法(该值大于0即说明系统具有混沌特征)。但如果计算得到的最大Lyapunov指数小于或等于0，说明该涌水量不具有混沌特征或混沌特征不明显，建议采用其他方法进行涌水量的预测。

5 结 论

1)矿井水文系统具有循环迭代特征，具备了产生混沌现象的条件。

2)根据混沌理论和广义回归神经网络特有的优势，建立了涌水量预测的Chaos-GRNN模型。该模型利用相空间重构确定了矿井涌水量影响因素的数目及其取值，该值与GRNN输入层神经元的个数和取值相对应，模型预测时长由最大Lyapunov指数决定。

3)对平煤十二矿建立了涌水量预测的Chaos-GRNN模型，模型克服了以往模型对涌水量影响因素考虑不够和难以量化的缺点，预测精度达到了94.98%。