基于组合权-改进灰色关联度理论的矿井突水水源识别

朱赛君，姜春露,2，毕 波，谢 毫，安士凯

(1.安徽大学 资源与环境学院，安徽 合肥 230601；2.安徽省矿山生态修复工程实验室，安徽 合肥 230601;

0 引 言

煤矿突水是煤矿灾害之一。快速精确的识别突水水源，是防治突水水害的关键工作之一。针对矿井突水水源识别问题，陈红江[1]、黄平华[2]基于Fisher判别分析理论，对不同含水层的水样进行判别分析；宫凤强[3]、王心义等[4]采用距离判别分析的方法建立了突水水源识别模型；徐星[5-6]、李垣志等[7]依据常规水化学离子浓度，建立以人工神经网络为基础的矿井水源识别模型；张瑞刚等[8]利用水质指标作为判别因子，结合可拓识别方法，建立了突水水源识别模型；DUAN[9]、胡伟伟等[10]基于矿区的水文地质条件建立了以水文地球化学和同位素分析为基础的矿井水源识别模型。此外，判别突水水源的方法还有水温水质识别方法、聚类分析方法、灰色关联理论、支持向量机识别等[11-17]。其中灰色关联度理论主要通过序列的几何关联度来分析各因素之间的关联程度，对于矿井突水水源识别有一定的效果。目前，灰色关联理论已经在灾害预测与评价、工程管理等领域成功运用[18-20]。

虽然灰色关联理论的应用取得了一定的成果，但也有不足之处。一方面由于灰色关联度的计算中分辨系数ρ的值通常按照经验取0～1，分辨系数ρ的取值不同会造成灰色关联度的差异；另一方面灰色关联理论一般按照单一赋权法确定各指标权重，无法综合考虑主客观情况，导致赋权结果具有偏向性，从而影响了模型的识别精度。为了克服上述不足，采用方差法对分辨系数ρ进行改进；利用熵权法确定客观权重，改进层次分析法确定主观权重，结合改进灰色关联度理论，建立组合权-改进灰色关联度理论的突水水源识别模型，从而提高水源识别模型的准确性与适用性，为矿井突水水源的识别提供了新的方法。

1 灰色关联理论研究方法

1.1 灰色关联度分析

灰色系统理论所研究的对象是带有不确定性质的系统，可用来处理一些模糊集、概率论难以解决的不确定问题。它通过描述、分析、综合已知的信息，从而确切描述和认识问题[21]。其中灰色关联分析是灰色系统理论的主要内容之一，其基本原理是利用因素之间发展趋势的相似程度来衡量因素间的密切程度，随着相似程度的增大，则因素间关系的密切度增大，关联度就越大。水源识别中的水样化学组分是由多个指标来组成的，每个水样的多个化学指标就构成了一个有序的序列，通过建立模型，构建了一个已知序列，待判的突水样品通过与已知进行比较，从而得到判别效果。

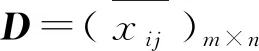
(1)

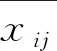
关联系数li(k)的计算公式为

(2)

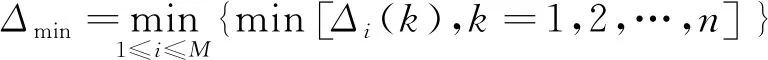
由于在实际计算过程中，式(2)中的分辨系数ρ的取值一般根据经验取0～1，且关联系数会随着ρ的变化而变化。为了避免分辨系数ρ取值不同而产生的误差，通过方差法对分辨系数进行了改进[22]。将标准化后的背景值作为研究对象，求出每一列水化学指标的标准差σi(i=1,2,…,6)。比较得出标准差最大值σmax以及最小值σmin，利用方差法来确定分辨系数ρ，降低了两级最大绝对差的影响。改进后的关联系数公式为

(3)

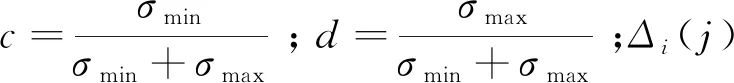
1.2 组合权值的确定

组合权重方法综合考虑了客观权重与主观权重，使各识别因子的权重更加合理[23]。客观权重由熵权法确定，通过计算某个指标的信息熵，将待评价指标的信息进行量化，可以反映该指标提供的信息量的多少以及信息的效用，从而确定该指标在综合评价中的作用大小[24-25]。熵权法的基本思想[26]是依据各指标所提供的信息量的多少来决定相应指标的权重系数的大小，其优点在于最大程度地减小了主观确定权重带来的人为干扰。

对评价指标进行标准化，消除量纲的影响，标准化公式如下：

(4)

式中，rij为对xij进行标准化之后得出的结果。

计算评价指标的熵值，如果指标的信息熵越小，该指标提供的信息量越大，在综合评价中所起作用越大，权重就应该越高。熵值计算公式如下:

(5)

式中，当rij=0时，Ej=0；Ei为对rij求熵值得出的结果。

熵权法中确定客观权重τi公式为

(6)

主观权重由改进层次分析法确定[27]，比较6个识别因子的重要性，得出判断矩阵P：

(7)

其中，若aij=1，则说明i比j重要；若aij=-1，则说明j比i重要；若aij=0，则说明两者同样重要。

P的最优传递矩阵A：

(8)

A的判断矩阵为B：

(9)

式中，bij=exp(gij)。

识别因子的主观权重值δi为

(10)

确定组合权值ωi:

(11)

最后求出灰色加权关联度Wi：

(12)

ωi为得出的组合权值；ζij为灰色关联系数,

2 矿井突水水源识别

2.1 研究区概况

潘谢矿区隶属于淮南煤田，位于阜东矿区与淮南矿区之间，自西端阜阳境内延伸，至东部滁州市内，区内主要水系为淮河(图1)。

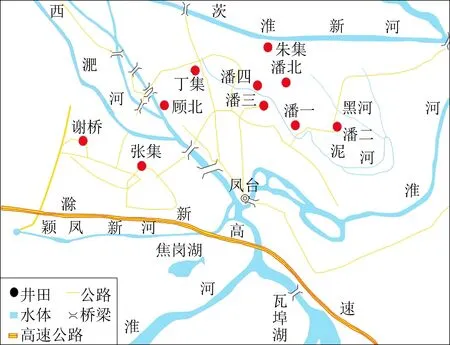
图1 研究区地理位置

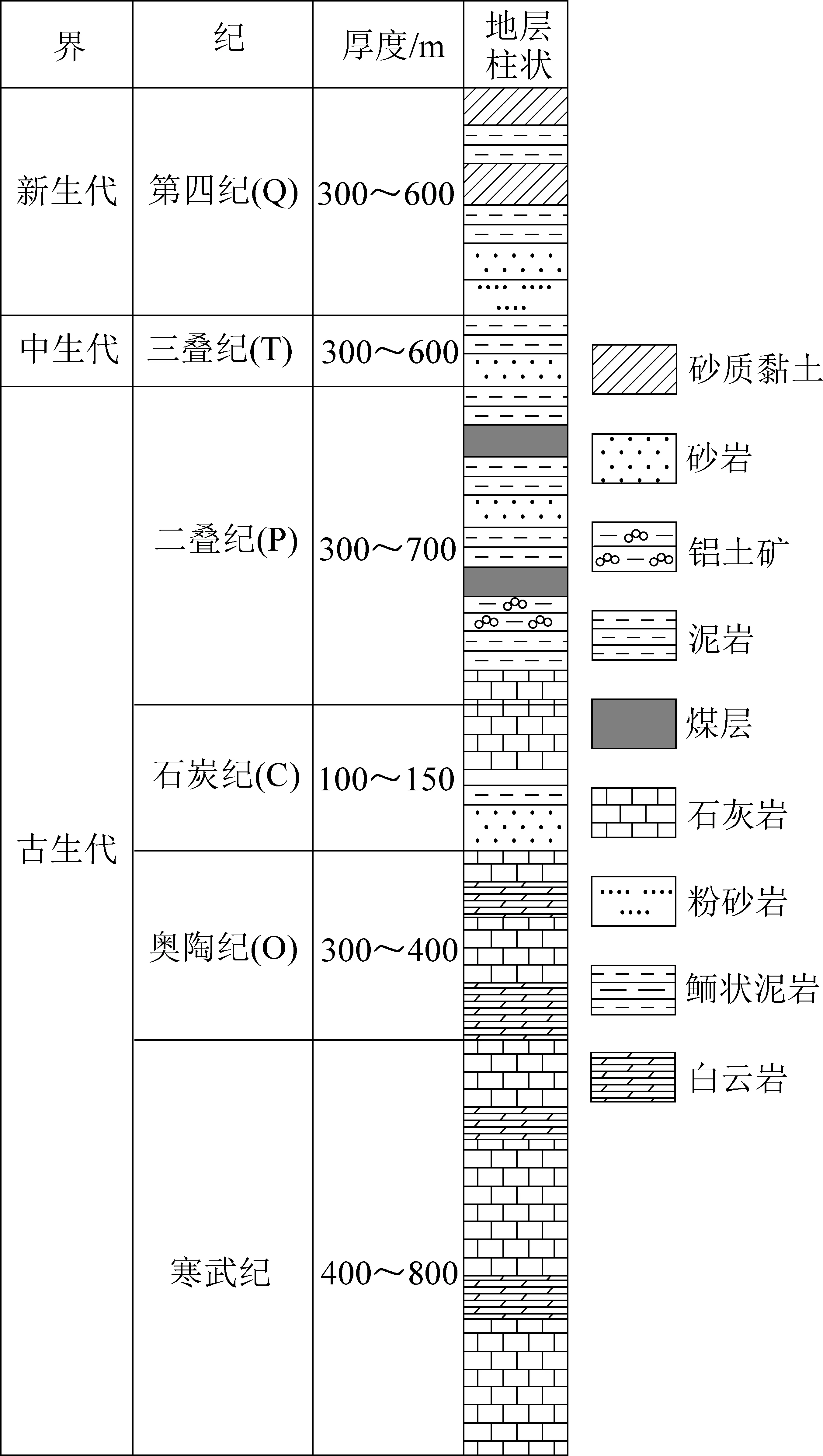
图2 研究区主要含水层

2.2 突水水源识别模型的建立

将学习样本不同含水层的水样指标浓度均值分别与检验样本的水样指标浓度的均值进行比较。由图3可以看出，相同含水层的学习样本与检验样本的水样指标浓度变化程度更为相近，关联程度也更高。符合灰色关联理论即：在系统发展过程中，如果2个因素变化的趋势具有一致性，两者同步变化程度较高，即可谓2者关联程度较高，两者为一类的几率也越高。

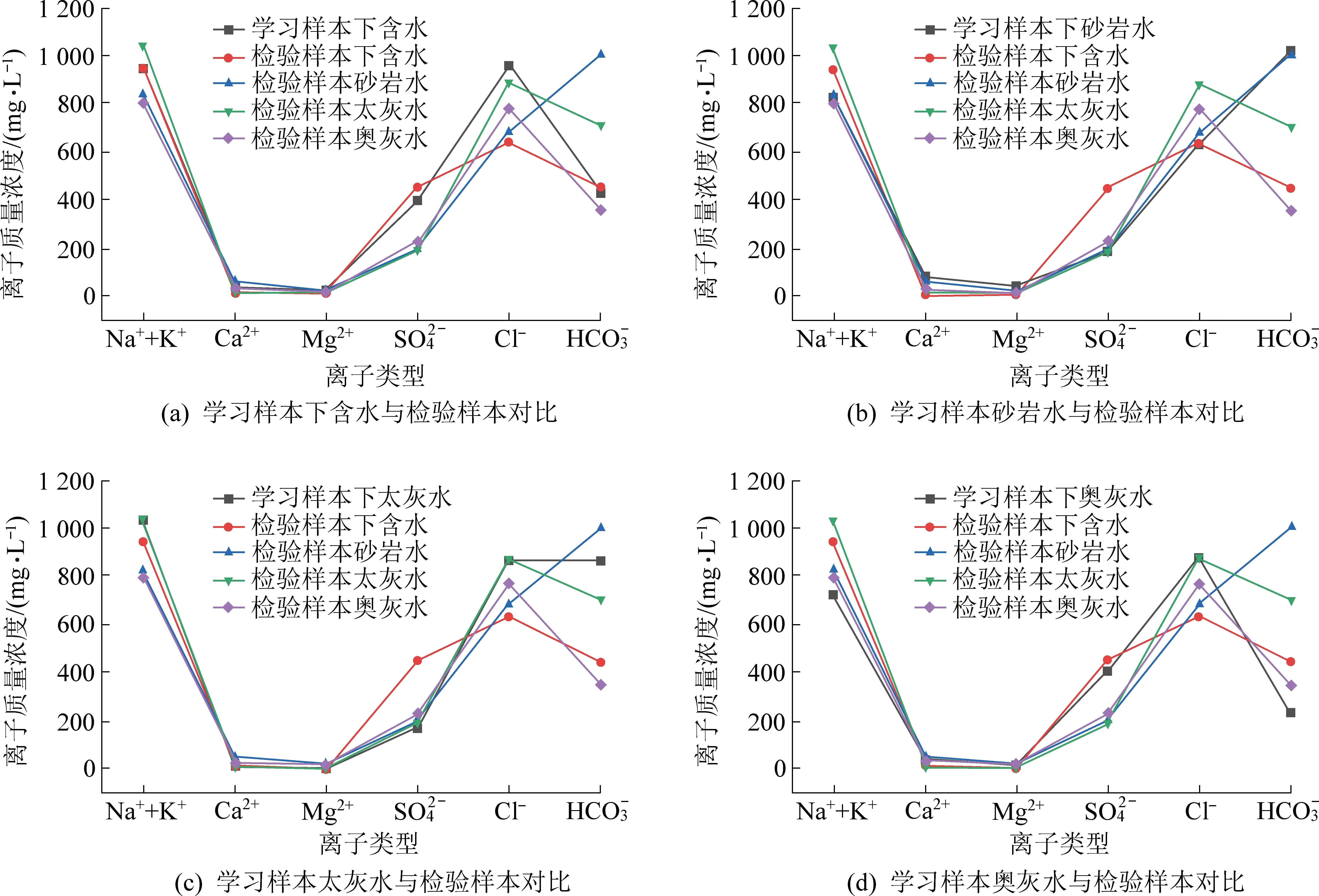
图3 学习样本与检验样本各指标含量变化比较

以4类水35组潘谢矿区的水样作为学习样本，建立识别区间，水样进行均值变换后的数据见表2。根据式(1)可得学习样本均值计量变换值，结果见表3。

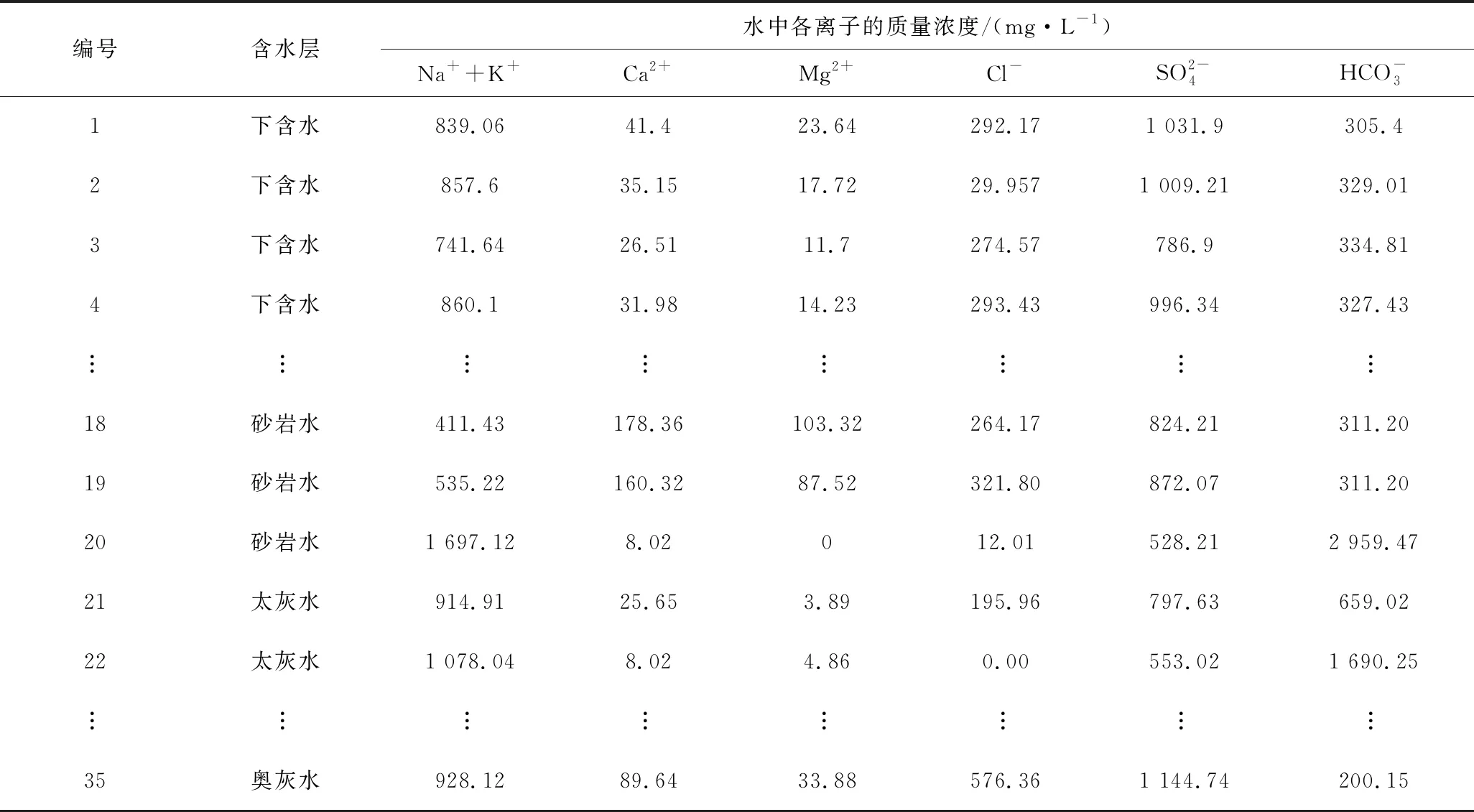
表1 潘谢矿区水样主要水化学成分

表2 学习样本标准化后背景值

表3 含水层学习样本背景值均值计量变换结果

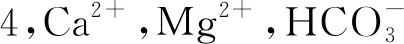
2.3 突水水源识别结果

取潘谢矿区的7个已知含水层水样作为水源识别模型的检验样本，其主要的水化学指标见表5，检验样本的均值计量变换结果见表6。

表4 学习样本判别指标权重

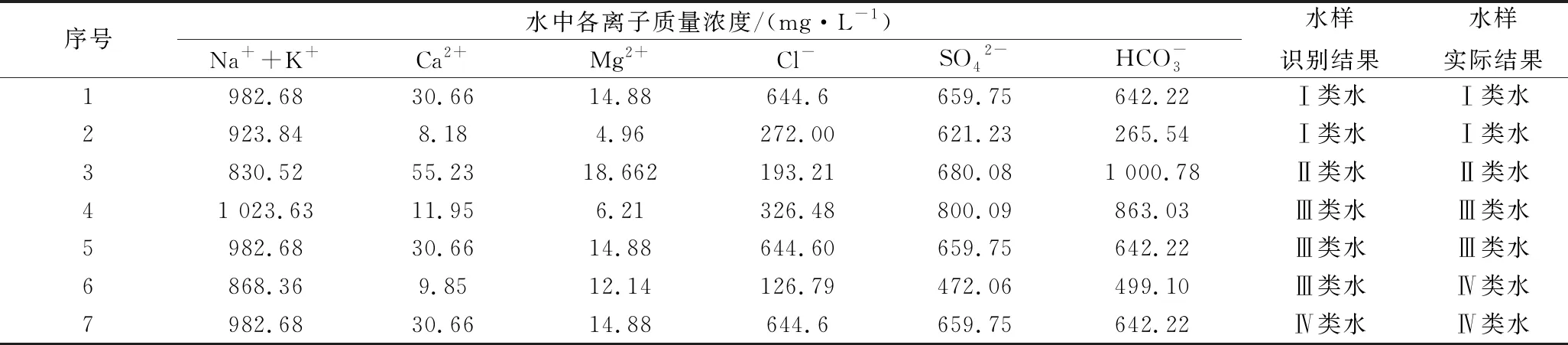
表5 检验样本水化学信息及识别结果

表6 检验样本背景值均值计量变换结果

按照灰色关联度理论，对表1中的学习样本与检验样本进行关联度分析，计算得出各个含水层不同指标的关联系数li(k):

(13)

由表2可知含水层各个指标的权重，利用式(12)可以得出不同类型含水层的加权关联度结果(表7)，综合计算和分析可知，7个检验样本的加权关联度最高分别是0.920,0.941,0.975,0.967,0.915,0.922,0.963，即判别结果显示检验样本分别属于Ⅰ、Ⅰ、Ⅱ、Ⅲ、Ⅲ、Ⅲ、Ⅳ类水。

表7 学习样本与检验样本关联度

应用组合权-改进灰色关联度理论水源识别模型对7组检验样本进行识别，有6组与实际完全相符，只有检验样本6被误判为太灰水，其准确率为86%。导致水样识别不准的原因可能是奥灰水与太灰水含水层相近，水样在天然导水通道发生了混合，且两个含水层的水化学特征相似，从而导致了模型产生误判。因此在后续工作中应该进一步丰富水样的数据资料，增强模型在奥灰水和太灰水识别方面的适用性，提高模型的识别精度。

3 结 论

2)引用新的样本对模型进行检验，结果表明，7组检验样本中，有6组水样的识别结果与实际情况完全相同，该水源识别模型的准确率达到86%，说明该模型具有一定的准确性、适用性。

3)模型出现误判的原因可能是由于奥灰水和太灰水的含水层相近，水样在天然导水通道发生了混合，且两组水样的水化学特征较为相似，模型难以区分。因此在后续工作中应该丰富水样信息，提高模型的精度。