岩石PFC2D模型细观参数确定方法研究

郝保钦，张昌锁，王晨龙 ，任 超

(1. 太原理工大学 矿业工程学院，山西 太原 030024；2.太原理工大学 机械与运载工程学院，山西 太原 030024)

0 引 言

常规岩石室内试验是研究岩石力学性质的主要手段。受限于试验设备和测试手段，岩石力学试验一般只能得到岩石试件的宏观变形和强度特性，而无法真正揭示岩石细观层面的力学行为。颗粒流程序(PFC)基于离散单元方法，将岩石类材料视为刚性颗粒的集合体，克服了传统连续介质分析方法在研究岩石类非均质材料时的局限性，可以从细观角度再现裂纹的孕育、扩展以及贯通的时空演化规律，已成为研究岩石力学问题的有效手段之一[1]。

二维颗粒流程序(PFC2D)通过定义颗粒接触的本构关系再现岩石宏观力学性质，接触黏结模型(CBM)、平行黏结模型(PBM)和平直节理模型(FJM)是最常用的3种细观本构模型。不论选取哪种模型，都需要不断调整细观参数来匹配宏观力学性质。目前大多数研究普遍采用“试错法”进行标定[2-3]，调整过程盲目性大、费时费力。国内外学者针对此问题展开了大量研究，进行了一定的改进。刘新荣等[4]以接触黏结模型中的等效微梁模型为基础，经过详细的理论推导确定了细观强度参数与岩石断裂韧度之间的关系。由于接触黏结模型颗粒接触界面不能抵抗转矩，平行黏结模型更广泛地被用于模拟岩石材料。文献[5-8]将理论分析与数值模拟相结合，系统地分析了平行黏结模型细观参数对宏观特性的影响，并给出了两者之间的量化关系。POTYONDY等[1,9-11]研究表明，受颗粒形状的影响，平行黏结模型不能很好地反映岩石的拉压强度比和强度包络线。为此，CHO等[10]分别提出了簇平行黏结模型[10]和平直节理模型[11]，通过抑制颗粒破坏后的旋转，使得拉压强度比显著减小。邓树新等[12]采用PB(Plackett-Burman)试验设计分析平直节理模型细观参数对宏观参数指标的敏感性，PB设计针对每个因素只能选取2个水平，当因素范围较大时可能会影响分析结果。

上述研究在颗粒流细观参数与岩石宏观力学响应关系的建立方面取得了富有成效的进展，同时也存在一定的不足。以往研究大多集中在单轴压缩、单轴拉伸和巴西劈裂试验上，而对于有围压的三轴压缩试验研究较少。对平行黏结这一最常用模型进行宏细观参数研究时，相关学者[1,9-11]做了一定的假设。对于摩擦因数和黏结摩擦角这些可能对宏观力学响应有重要影响的细观参数并未做深入的研究。鉴于此，针对PFC2D中的平行黏结模型，基于正交设计原理，通过一系列的实验室试验(单轴压缩、单轴拉伸和三轴压缩)系统全面地分析细观参数与宏观参数间的关系。

1 正交试验设计

1.1 正交试验设计原理

在科学试验中常会遇到试验结果受多种因素影响的情况。若采取全面试验的方法，其工作量将随因素的个数呈指数形式剧增。正交试验设计是一种优化的试验方法，它利用正交表科学安排因素组合，能够在明显减少试验次数的前提下得到可靠性较强的试验结果[13-14]。通过多因素方差分析可以评估众多因素对试验指标的影响程度。因此，采用正交试验设计法对PFC2D平行黏结模型宏细观参数关系进行研究，量化参数对应关系，为参数标定提供依据。

正交表是正交试验设计中安排试验和分析结果的基本工具，一般用Ln(rm)表示。其中，L为正交表代号；n为试验次数；r为因素水平；m为因素数量。正交表具有2个重要性质：表中任一列不同因素水平出现的次数均相同；表中任意两列同行水平组成的数字对出现的次数相同。

1.2 方差分析

方差分析可以精确量化试验因素对试验结果的影响程度，通过计算因素的离差平方和与误差的离差平方和，并基于此构造F统计量。对于给定的显著性水平α，可以查F分布表得到对应的临界值F1-α。当F值大于临界值F1-α时，认为该因素对试验结果有显著影响。

若采用Ln(rm)正交表设计试验，y1，y2，…，yn为试验结果，方差分析的基本步骤如下。

1)计算总离差平方和SST。

(1)

其中，

(2)

(3)

2)计算因素j引起的离差平方和SSj。

(4)

其中，

(5)

(6)

式中：Ki为第j列水平号为i的试验结果之和。

3)计算试验误差的离差平方和SSe。

SSe=∑SSk

(7)

式中，SSk为空列离差平方和。

4)计算自由度。SST和SSj的自由度分别为

fT=n-1

(8)

fj=r-1

(9)

误差的自由度为

fe=∑fk

(10)

式中：fk为空列自由度。

5)计算F值。

(11)

6)显著性检验。对于给定的显著性水平α，当Fj>F1-α(fj,fe)时，则该因素对试验结果有显著性影响。Fj相对F1-α(fj,fe)越大，则该因素对试验结果的影响越显著。

2 试验指标及试验因素

2.1 试验指标选取

岩石力学试验是测试岩石在不同受力条件下(即单轴压缩、单轴拉伸和三轴压缩等)的破坏及变形特性参数，通过岩石力学试验可以得到岩石材料的力学参数包括抗压强度、抗拉强度、弹性模量以及泊松比等。

目前关于参数标定的大多数研究都是针对单轴压缩试验展开的，通过不断调整细观参数对应力-应变曲线进行拟合。陈鹏宇等[15]研究指出，仅通过单轴压缩试验标定得到的颗粒流数值模型，并不能直接用于研究有围压条件下岩石的力学性质。自然界的绝大多数岩石都处在三向应力状态，研究岩石在三向应力状态下的强度和变形特征对于指导岩土工程设计具有重要的意义。强度包线可以全面反映三轴试验的强度指标值，因此选择它作为参数标定的依据。强度包络线包括黏聚力和内摩擦角2个宏观力学参数，对于库伦强度包线，黏聚力可以由单轴抗压强度和内摩擦角表示，因此仅选取内摩擦角作为试验指标。

岩石的抗拉强度是反映岩石力学性质的重要指标之一。岩石的抗拉强度远小于其抗压强度，在受荷不大时就可能出现拉伸破坏，因此进行数值仿真时应将拉伸强度作为重要的标定依据。POTYONDY等[1,9-10]采用平行黏结模型模拟Lac du Bonnet花岗岩材料时发现，其抗拉强度与抗压强度的比值显著大于实验室的测量值。但以上的研究对一些参数如摩擦因数μ、黏结摩擦角φ以及黏结强度变异系数Cv等的选取并不充分，它们对于拉压强度比的影响还不明确。

启裂强度是裂纹萌生和稳定扩展的标志，它对估算岩体隧洞松动圈范围、指导围岩支护有重要的意义。室内试验常通过计算裂纹体积应变[16]，或结合声发射试验结果确定岩石试件的启裂强度[17]。采用PFC模拟岩石试件可以记录试验加载过程中的裂纹数目及扩展情况，可以结合裂纹数目判断试件的启裂强度。POTYONDY等[1]通过裂纹数目的变化来确定启裂强度，认为裂纹数目达到峰值强度裂纹数目1%时所对应的强度即为启裂强度。数值模型相对半径范围较大，为兼顾所有数值模型，选取10%为启裂强度的判断条件。

2.2 试验因素确定

采用平行黏结模型(PBM)模拟岩石室内试验。平行黏结模型将岩石表示为具有有限厚度圆盘的组合，圆盘之间通过黏结键相连，圆盘之间的接触以及黏结区域具有有限刚度。当施加的局部应力(即张力、剪切力或旋转力矩)超过规定的键的强度时，这些键断裂形成一个微裂纹。在这些过程中，PFC不需要任何描述屈服后响应流动规律来控制断裂行为，只需要颗粒的运动规律、颗粒变形的简单本构规律和颗粒键断裂的屈服规律。平行黏结模型参数主要包括颗粒细观参数和黏结细观参数，具体见表1。

表1 PFC2D模型主要的宏细观力学参数

2.3 试验因素范围

在颗粒离散元模型中，黏结破坏后颗粒间的滑移与摩擦因数μ有关，POTYONDY等[1]认为摩擦因数可能会影响材料的峰后行为，建议对于岩石材料μ取0.5。CHO、程爱平等[10,18]认为颗粒间的摩擦力会抑制颗粒的运动，从而提高材料的强度。为了研究μ对宏观参数的影响，设定μ的取值范围为0.2～0.8，这与文献[10,12,15]的取值相近。

文献[19]表明能够体现材料统计平均性质代表性体积单元的尺寸至少应该是颗粒尺寸的7～8倍。周喻等[20]研究发现，当RES=(L/Rmin)[1/(1+Rmax/Rmin)]≥10，即L/Rmin≥26.6(Rmax/Rmin=1.66)时，计算结果离散性不大。尹小涛等[21]研究表明，材料内尺度比非常小时，它对模型特性几乎无影响，但会造成计算时间急剧升高。兼顾计算精度和计算效率，设定L/Rmin取值范围为30～120。

陈鹏宇等[15,23]利用单轴或三轴数值试验展开了黏结内摩擦角φ与宏观力学参数关系的研究，结合他们的研究成果，将φ的取值设定为0°～60°。

变异系数Cv是黏结强度标准差与强度均值的比值，反映了模型细观强度的不均匀性。阿比尔的等[6]研究发现Cv<0.2时，模型强度参数趋于稳定，Cv取值过大则会造成强度参数偏小，因此将Cv的取值设定为0.2～0.8。

3 细观参数敏感性分析

3.1 正交试验设计方案及计算结果

根据因素个数与因素水平，采用L32(49)正交表设计试验。依据因素水平可设置32组参数组合。基于参数组合分别进行单轴压缩、直接拉伸和三轴压缩试验(围压分别为5、10、15、20 MPa)，共计192组数值试验，具体结果见表3。数值试样长度H=100 mm，宽度L=50 mm，密度ρ=2 700 kg/m3。

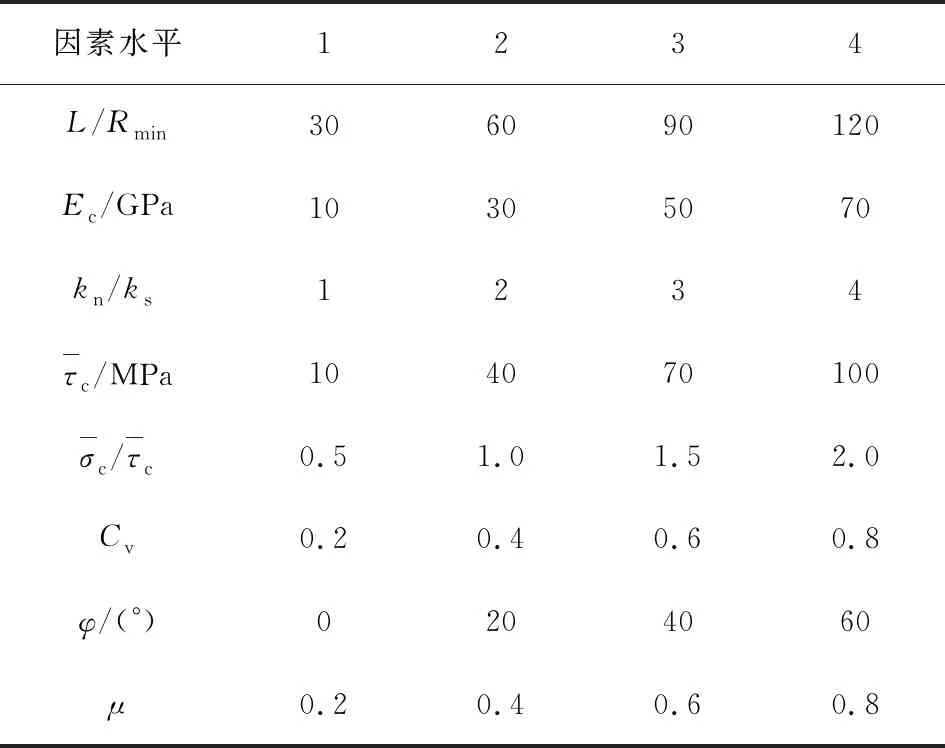
表2 各参数因素水平

对表3的正交试验设计结果进行初步的分析，数值模型试件的拉压强度比σt/σc是关注的重点。岩石的抗拉强度一般为抗压强度的1/25～1/4，平均为1/10[24]。对表3中的结果进行统计可以得到拉压强度比在0.09～0.46，这基本满足了大部分岩石的标定需求。同时也表明采用平行黏结模型模拟岩石试件时，全面地对细观参数进行合理取值就可以得到较小的拉压强度比。

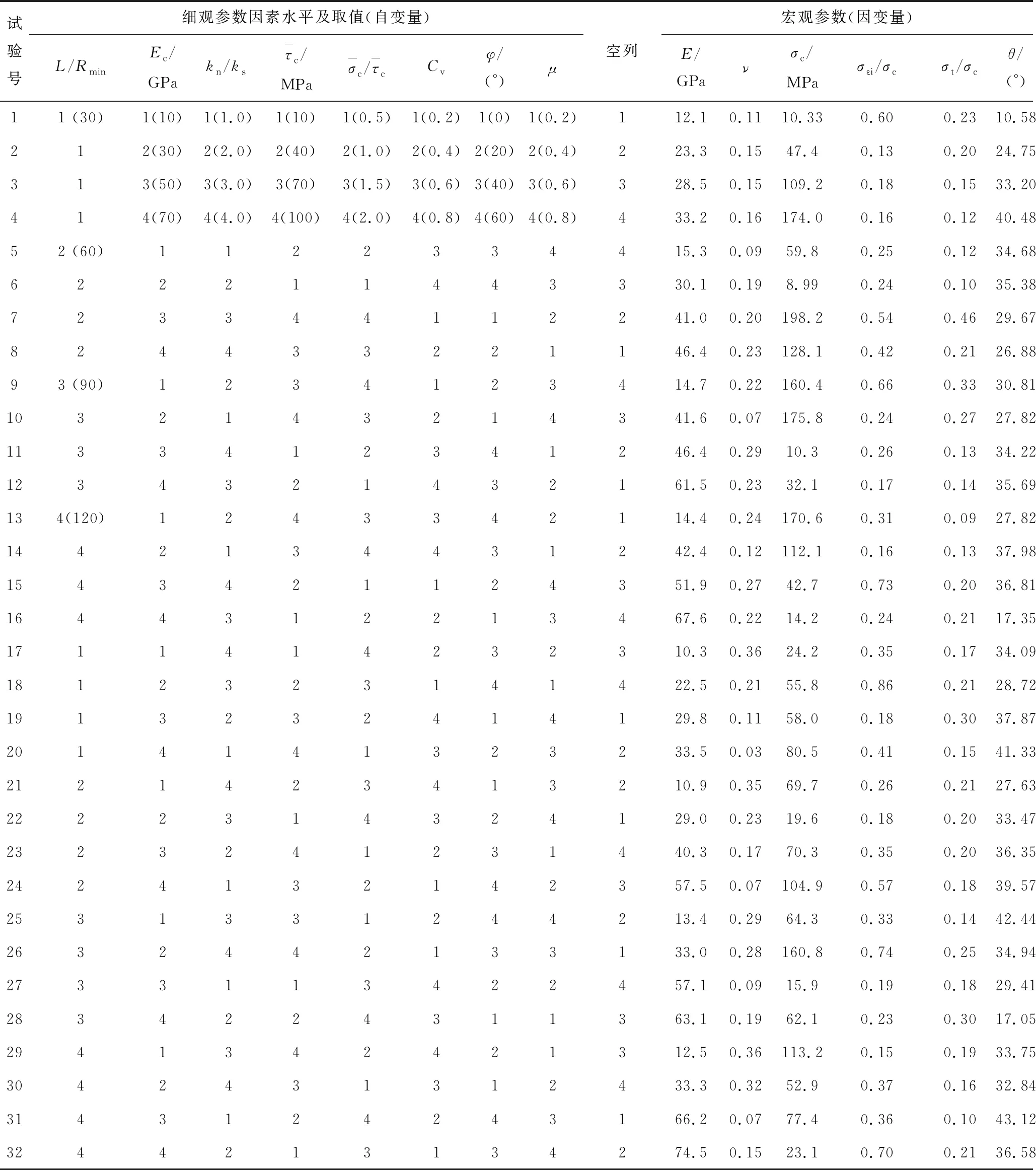
表3 基于正交试验设计的数值计算方案及结果

3.2 正交设计结果分析

对数值计算结果进行方差分析见表4。根据式(5)和式(8)分别计算因素和误差的离差平方和。根据公式(10)可计算得各因素自由度f=r-1=4-1=3，误差自由度fe=3。计算选定显著性水平α=0.01，F0.99(3,3)=29.46。当F≥F0.99(3,3)时，认为因素j对试验结果有非常显著影响，记作“**”。对于显著性水平α=0.05，F0.95(3,3)=9.28。当Fj≥F0.95(3,3)时，认为因素j对试验结果有显著性影响，记作“*”。为更直观地分析试验因素对试验指标的影响程度，将方差分析结果绘制成柱状图，如图1所示。

表4 方差分析

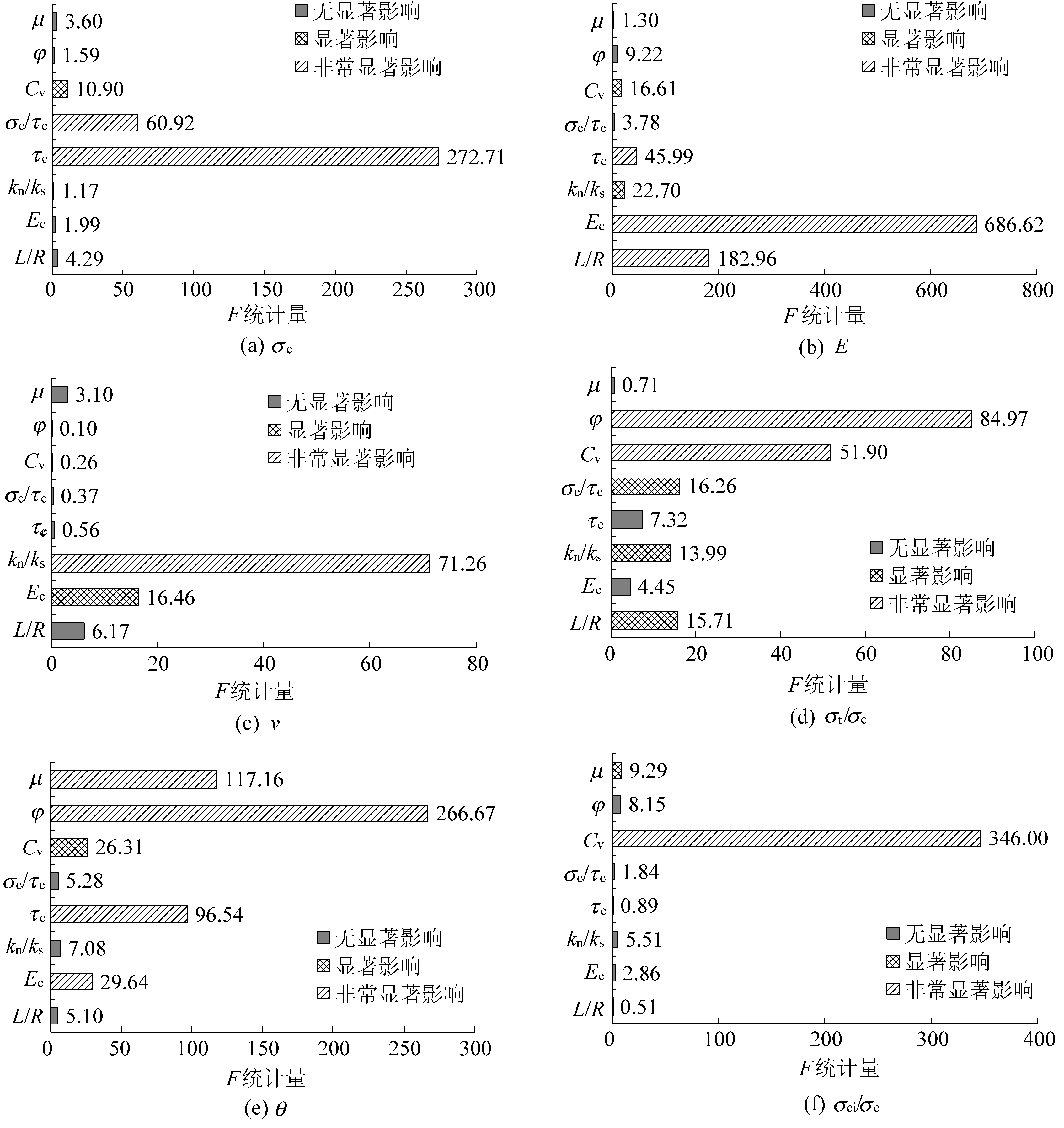
图1 多因素方差分析F统计量

结合表4和图1的方差分析统计结果可以看出，试验因素对试验指标影响程度各不相同，具体分析如下：

3)图1c显示，对试块泊松比ν有非常显著影响的只有刚度比kn/ks这1个细观参数。虽然Ec和L/Rmin达到了著影响水平，但他们对ν的影响可以忽略。

6)图1f有且仅有一个试验因素Cv对启裂强度与单轴抗压强度比值σci/σc有非常显著的影响。通过多因素方差分析，可以从众多的细观参数中筛选出对试验指标有显著性影响的因素。对显著性影响因素与试验指标进行回归分析，可以得到宏细观参数间的对应关系：

(12)

ν=0.144ln(kn/ks)+0.080 (R2=0.70)

(13)

(14)

(15)

(16)

(17)

4 标定方法及应用

4.1 标定方法

图2 细观参数标定流程

4.2 实例验证

以锦屏二级水电站深埋白山组大理岩[25-26]为研究对象，采用上述方法进行细观参数标定。对比大理岩力学试验及声发射试验结果，验证标定方法的可行性。表5再现了细观参数标定过程，共进行了5次调整过程。式(12)—式(17)反算可以得到步骤1的初始细观参数，此时对应的宏观参数与目标值接近，但仍有一定的差距。这是因为细观参数数目众多，回归分析时只考虑了对宏观参数有显著性影响的细观参数，而影响不显著的参数可能对试验结果有一定的影响。 步骤2～6参考图2的标定流程，对细观参数进行了适当的调整。将试验平均值与模拟值汇总在表6中，除内摩擦角以外，其他模拟结果与目标值之间的误差均在7%以内，可认为标定结果符合要求，结束标定。

表5 大理岩宏观参数试验值与模拟值

表6 大理岩细观参数标定过程

将数值模拟试验和物理试验获得的单轴压缩应力-应变曲线绘制在图3中。可以看出两者曲线基本重合，但存在一定的区别。大理岩试件中存在的微裂隙会在压力作用下产生闭合，应力-应变曲线会出现明显的压密阶段。而数值模拟在生成颗粒时采用了一定伺服压力，使产生的颗粒集合体接触致密、均匀，因此其应力应变关系峰前阶段近似为一条直线。

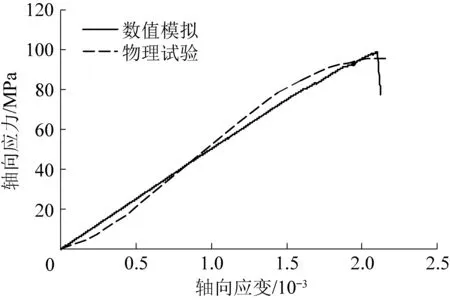
图3 物理试验和数值试验的单轴压缩应力-应变曲线对比[26]

莫尔-库仑强度准则因其简单实用而在岩土工程领域得到广泛应用，可以用来表征强度包络线。该准则在主应力平面上呈线性关系，即

(18)

因此，若已知σ1与σ3间的关系就可以求得黏聚力C和内摩擦角θ。

(19)

(20)

式中：k为极限主应力(σ1-σ3,σ1为最大主应力，σ3为最小主应力)关系曲线斜率[24]；σc为极限主应力关系曲线在纵坐标轴上的截距。

图4为数值试验与室内试验极限主应力关系曲线对比，试验曲线参考文献[26]中σ1-σ3拟合曲线。根据拟合曲线，由式(18)—式(20)可计算得到岩石的内聚力和摩擦角，将计算结果标注在图4中。可以看出，当围压较小时，数值模型预测的极限轴向应力与试验结果较接近，而随着围压的增大，他们之间的差值也逐渐增大。这可能是由于PFC基于离散单元方法，将岩石类材料视为圆形/球形颗粒的集合体，而实际岩石矿物颗粒形状则为不规则的多面体。形状的不同可能会导致颗粒间的咬合作用产生差异，而围压的增加则放大了这种差异。POTYONDY 等[1,12]研究也指出颗粒离散元法在极限主应力关系曲线的拟合上存在一定困难。

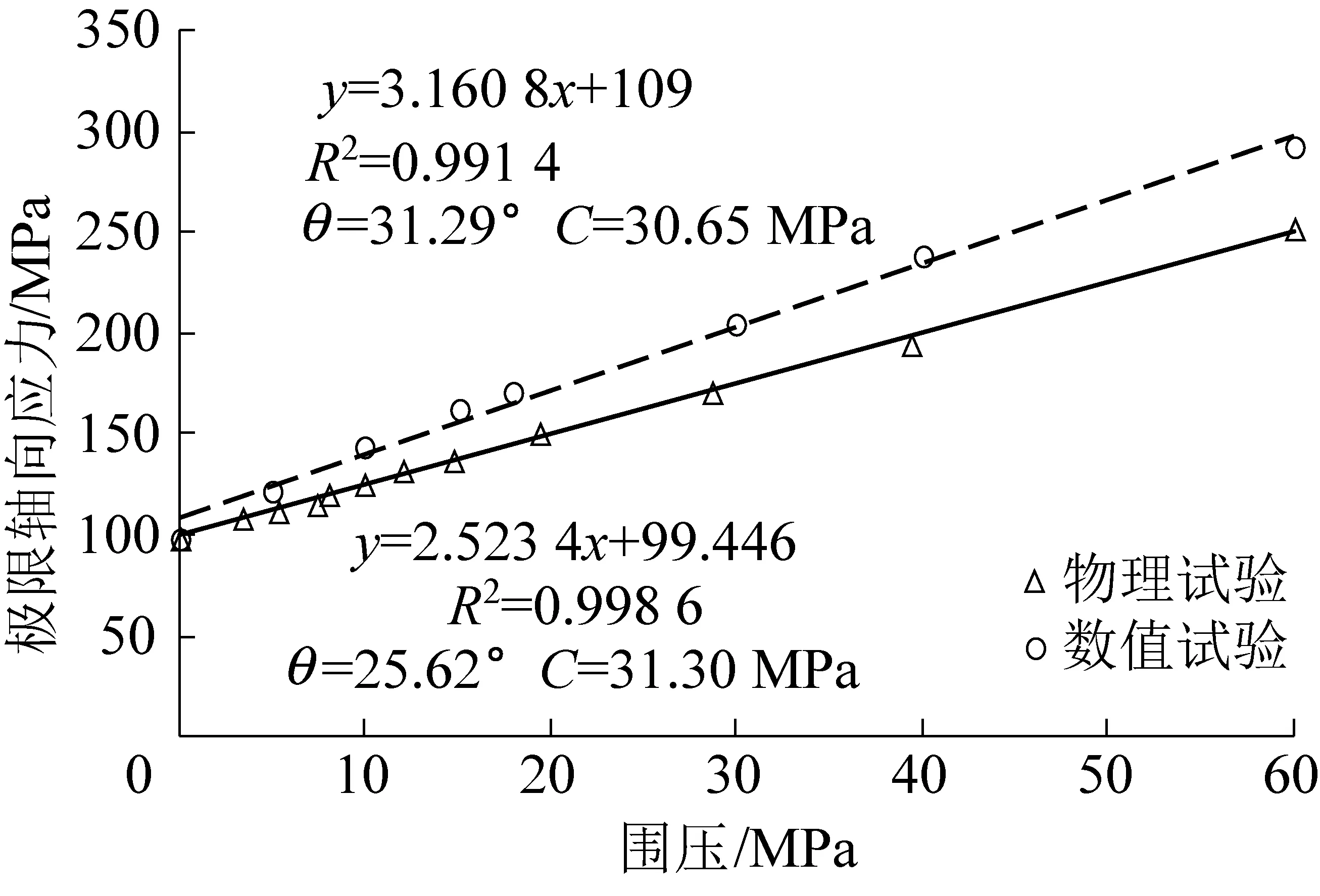
图4 极限主应力关系曲线[26]

将数值试验得到的试件破坏形式实际物理试验进行对比，如图5所示。对比发现不同加载条件下的数值试验与物理试验结果吻合性较好。图5a单轴压缩试验试件的破坏形式表现为沿剪切带的整体滑移破坏，同时与主要滑移面斜交方向产生1个次生破坏面。图5b围压18 MPa下的三轴压缩试验试块均出现了宏观剪切破坏带(其他围压条件下试件破坏形式也一致)。

图5 破坏形式对比[26]

5 结 论

1)通过对正交试验结果进行多因素方差分析，精确估计了各细观参数对宏观参数的影响程度。岩石单轴抗压强度主要受黏结切向强度和黏结强度比的影响；岩石泊松比主要受刚度比的影响，它们之间呈对数关系，泊松比随着刚度比增大而增大；对岩石的宏观弹性模量有显著影响的细观参数，影响程度由高到低为：细观弹性模量、相对半径及黏结强度比；岩石拉压强度比主要受黏结内摩擦角和黏结强度变异系数的影响，合理地调整细观参数可以使拉压强度比降至0.1左右，满足大部分岩石的要求；对岩石内摩擦角有显著影响的细观参数类型最多，影响程度由高到低依次为：黏结内摩擦角、摩擦因数、黏结切向强度以及细观弹性模量。

2)根据方差分析结果，综合考虑多个细观参数对宏观参数的影响，进一步建立了显著影响因素与试验指标间的多元函数关系。

3)根据宏细观参数间的关系，确定了细观参数的标定顺序，提出了具体的标定方法。并采用该方法对锦屏白山组大理岩力学参数进行了标定。数值试验与物理试验的宏观力学参数、破坏模式以及应力-应变曲线基本对应，验证了细观参数标定方法的可行性。

4)由于采用圆形颗粒，平行黏结模型对极限主应力关系曲线的拟合效果较差。