基于组合权重的地表下沉系数预测分析

栾元重，纪赵磊，崔 诏,2，梁耀东

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266590；2.黑龙江第三测绘工程院，黑龙江 哈尔滨 150025)

0 引 言

煤炭资源是我国的基础能源和重要原料，在能源消耗结构中占据重要地位[1]。煤炭资源的大规模开采会对地表建(构)筑物造成破坏，也会对生态环境产生严重影响[2]。因此，煤矿开采过程中的地表沉陷预测极其重要。

地表下沉系数是表征开采沉陷和地表移动规律的重要参数，也是进行地表移动和变形预测时的关键参数，其取值的准确性将直接影响沉陷预测结果的精度[3-4]。影响地表下沉系数的因素很多，因素间的不确定性及非线性关系使得下沉系数的预测工作极其困难，依靠地表观测站数据的实测下沉值或水平移动值反演地表下沉系数的方法耗时费力，不适合长期发展[5-6]。近些年来，随着人工智能算法的发展，越来越多的学者利用随机森林算法、遗传算法和支持向量机等模型进行地表下沉系数预测。彭杰帅等[7]利用随机森林算法不易出现过拟合的优势进行了地表下沉系数预测，王拂晓等[8]将遗传算法与广义回归神经网络相融合，建立了GA-GRNN的地表下沉系数预测模型，于宁峰等[9]建立了基于PSO优化参数的SVM预测模型实现地表下沉系数的预测分析。这些方法都是利用一种或几种算法的优势对地表下沉系数预测进行有益探索，具有一定的适用性。

笔者借助BP神经网络较强的非线性映射能力进行地表下沉系数预测，考虑到地表下沉系数的影响因素较多且因素间存在相关性，提出通过组合权重来确定主要影响因素，进而实现BP神经网络输入参数的预处理与模型简化。利用地表实测数据对由主要影响因素建立的BP神经网络预测模型进行了验证，得到了较高的预测效果，是地表下沉系数预测的又一种有效方法。

1 主成分分析法确定权重

主成分分析法(简称PCA)是常用的基础数学分析方法，其在数学建模、动力学模拟和数理统计等领域应用广泛。在众多领域的研究中，大量变量之间的相关性增加了问题研究的复杂性，因此考虑利用较少的不相关变量代替各个变量中的各种信息，主成分分析就是这样一种数据降维方法。PCA在能够保留大部分原始数据信息的情况下，将N维特征映射到K维上(N>K)，从而起到降低数据维数的作用[10]。

有N维数据集Xi，构造线性组合Y=AX，则主成分分析的数学模型[11]如下：

(1)

式中，Y为主成分；X为原始变量；a为主成分系数。Yi和Yj线性无关且ai1+ai2+…+aiN=1。

地表下沉系数影响因素众多，例如釆深、采厚、采宽、留宽、煤层倾角、覆岩岩性等[12]。受限于各个矿区资料收集的差异性，这里仅仅对国内35个矿区的开采厚度、煤层倾角、平均釆深、走向宽深比、倾向宽深比、推进速度、松散层厚度和覆岩平均坚固系数进行研究[13-14]，部分样本数据见表1，其信息描述见表2。

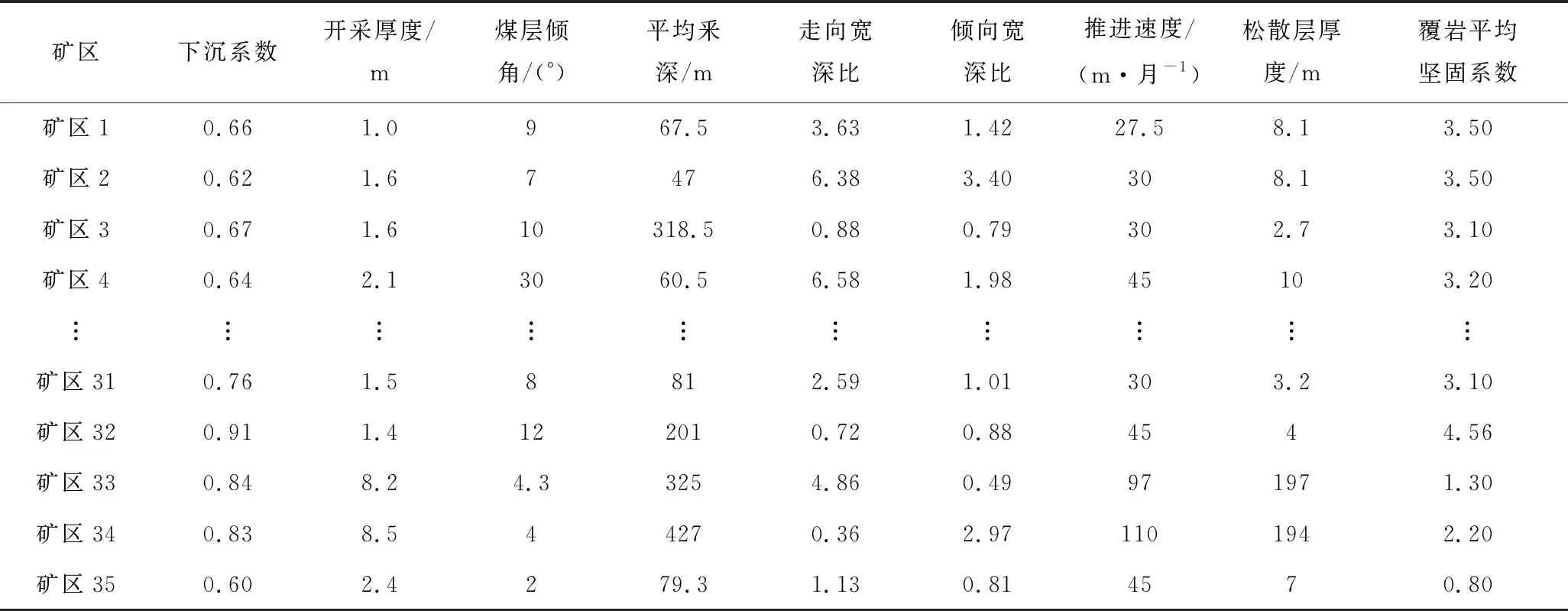
表1 矿区实测数据

表2 数据统计

利用SPSS20软件，对影响地表下沉系数的8个因素进行主成分分析。由软件计算得到的KMO>0.5和Sig<0.05可知(KMO和Sig为主成分分析的适用性)，可以对选取的8个因素进行主成分分析。根据累计方差贡献率大于80%的原则选取主成分，由表3可得，提取5个主成分，其方差贡献率分别为36.503%,20.350%,11.091%,10.565%和9.768%，累计方差贡献率达到88.276%。根据主成分系数与方差贡献率可确定各因素的综合系数，再将各因素的综合系数进行归一化处理，最后可以得到各个因素的权重[15]，见表4。

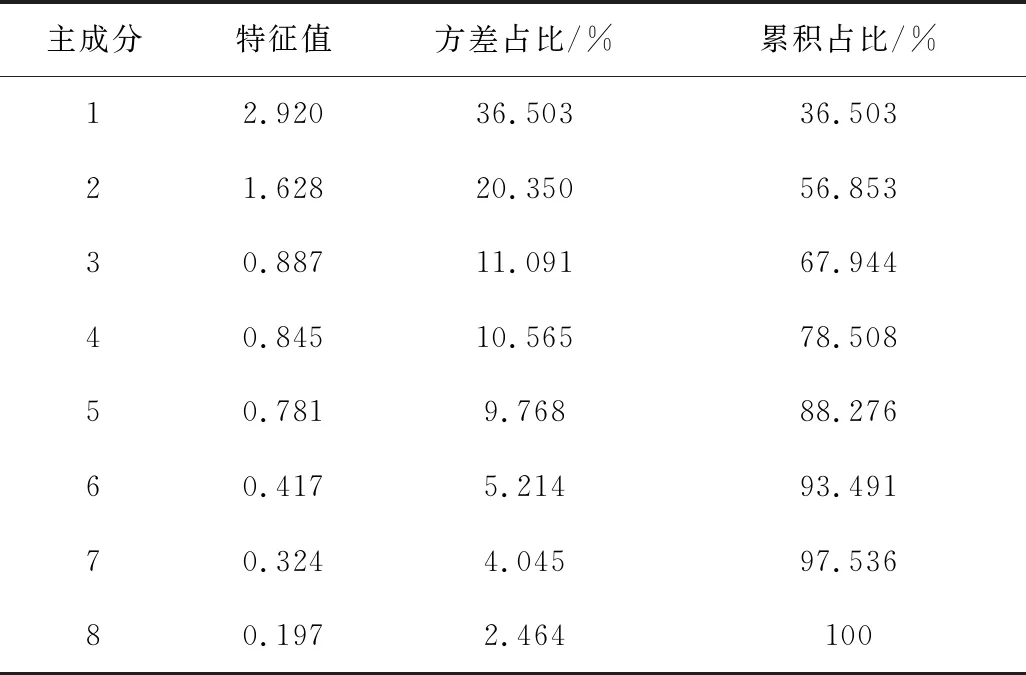
表3 方差解释

表4 主成分系数与因素权值

2 灰色关联度分析法确定权重

灰色关联度分析法(简称GRA)是灰色系统理论(我国著名学者邓聚龙教授于1982年提出)的一个重要分支，也是数据分析中常用的方法。灰色关联度分析的基本方法是根据比较数列集所构成的曲线与参考数列集所构成的曲线的相似程度来判断其关系是否密切，曲线形状越是相近，越说明相应数据系列关系越紧密[16-17]。该方法对样本数量的多少和样本规律性要求不够，且计算量小，不会出现反常情况。目前，灰色关联度分析法已成功应用到工程控制和农业经济等方面，都取得了不错的效果。

灰色关联度分析法确定权重的主要步骤如下[18-19]：

1)进行灰色关联分析时，首先要确定参考数列和比较数列，参考数列反映系统的行为特征，而比较数列是由影响系统行为特征的因素组成。

(2)

2)系统中各因素代表不同的物理意义，有着不同的量纲，而量纲的不同会导致最终的结论出错。因此，需要对数据进行无量纲化处理，将其归一到一个近似区域内，常用的处理方法有均值法和初值法。采用均值法进行数据处理的方式如下：

(3)

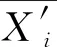
3)计算比较数列与参考数列对应因素的关联系数。

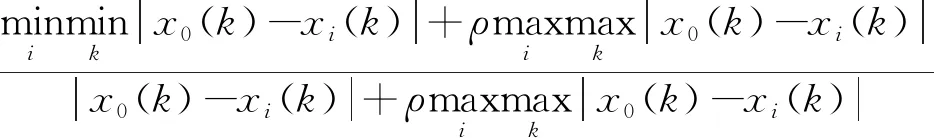
(4)

式中：i取值为1，…，M;k取值为1，…，N;ρ为分辨系数，反映关联系数间的差异性，通常取值为0.5。

4)计算关联度r(X0,Xi)。

(5)

5)根据关联度可得影响因素权重Wi。

(6)

以地表下沉系数为参考数列，以影响因素为比较数列，按照灰色关联度分析确定因素权重的步骤，对国内35个矿区的8个影响因素进行定权。由Matlab编程计算得到：开采厚度、煤层倾角、平均釆深、走向宽深比、倾向宽深比、推进速度、松散层厚度和覆岩平均坚固系数的灰色关联度分别为0.815,0.776,0.824,0.788,0.788,0.847,0.746和0.874；则各因素对应的权重为0.126,0.120,0.128,0.122,0.122,0.131,0.116和0.135。

3 地表下沉系数预测分析

3.1 组合权重确定主要影响因素

经主成分分析法定权和灰色关联度分析法定权后，各个影响因素的PCA权重和GRA权重见表5。根据参考文献[20]可知，由主成分分析法和灰色关联度分析法确定权重的公式如下所示：

W=0.5WP+0.5WG

(7)

式中，WP和WG分别为影响因素的PCA权重和GRA权重。

各影响因素的组合权重见表5。由组合权重可知，各影响因素对地表下沉系数的影响程度为：松散层厚度>推进速度>平均釆深>倾向宽深比>开采厚度>走向宽深比>煤层倾角>覆岩平均坚固系数。以权重大于0.13为主要影响因素的选取原则，选取松散层厚度、推进速度、平均釆深和倾向宽深比为主要影响因素。

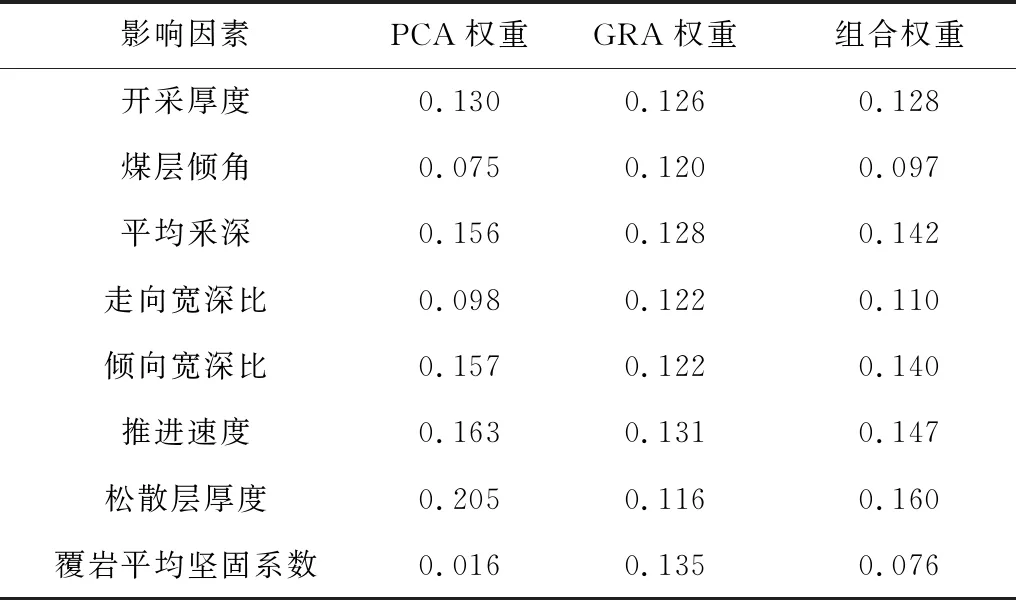
表5 影响因素组合权重

3.2 BP神经网络

BP神经网络是神经网络模型中应用最为广泛的模型之一，是一种信息前向传递、误差反向传播的多层前馈网络。它能够在数据间建立输入与输出的非线性映射关系，进而完成数据预测。研究证明，一个简单的3层BP神经网络就可以以任意精度与任意连续函数相拟合[21]，3层BP神经网络包括输入层、隐含层和输出层。

1)参数选取与数据预处理。以表1中的前32组数据作为训练样本进行网络训练，以后3组数据作为预测样本进行精度评价。以影响地表下沉系数的主要影响因素松散层厚度、推进速度、平均釆深和倾向宽深比为输入参数，以地表下沉系数为输出参数，建立4—N—1结构的BP神经网络模型，简称为W-BP模型。对于隐层节点N的选取，通过参考各种文献确定节点N的大致范围，然后经过“试凑法”进行多次训练[22-23]，分析实际模拟效果，最终确定N值为6。为使预测结果更为精确，在进行网络训练前，需要对数据进行归一化处理，消除数据间的数量级差别，并能够有效减小激活函数的函数误差，这里采用Matlab里的premnmx函数进行归一化处理。

2)网络参数与函数的设置。BP神经网络的激活函数(传递函数)能够引入非线性因素，进而解决线性模型无法解决的问题。因此，不同的激活函数会对预测效果产生不同的影响，借鉴以往研究成果，隐含层的激活函数选择S型正切函数tansig，输出层的激活函数选择线性函数purelin。学习训练函数和权重学习函数分别设为traingdx和learngdm，学习率设为0.01，训练目标误差为10-5。

3.3 预测结果分析

为更好地分析W-BP神经网络的预测效果，将其与传统BP神经网络(输入参数为8个参数)作对比。 在完成网络训练与仿真模拟后，通过分析预测值与实测值间的误差大小来检验模型的预测效果。误差对比见表6。

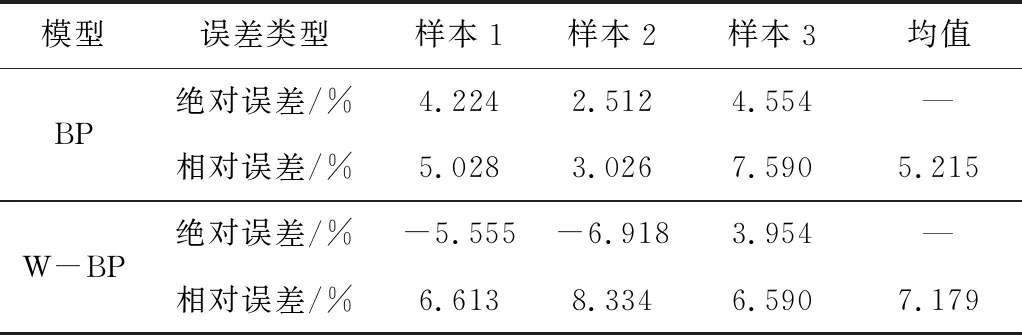
表6 误差对比

由表6可知，2种模型的绝对误差都小于7%，与实测值有着较好的拟合效果，但传统BP神经网络模型的整体拟合效果要优于W-BP模型。传统BP神经模型的平均相对误差为5.215%，W-BP模型的平均相对误差为7.179%，从相对误差对比可以发现，2种模型依然能够产生较好的预测效果，但传统BP神经网络模型的预测效果仍然优于W-BP模型。经分析可知，基于组合权重得到的主要影响因素虽然简化了BP神经网络模型，但缺失了部分信息，导致最终的预测精度低于传统BP神经网络模型。W-BP模型的绝对误差最大值为-6.918%，相对误差最大值为8.334%，能够满足基本工程需要，是地表下沉系数预计的一种可行方法。

4 结 论

1)利用主成分分析与灰色关联度分析相结合的方法求取地表下沉系数影响因素的组合权重，由组合权重分析各因素对地表下沉系数的影响程度，得到主要影响因素为松散层厚度、推进速度、平均釆深和倾向宽深比。

2)选取的主要影响因素实现了BP神经网络模型的简化，由绝对误差和相对误差对比分析可知，由主要影响因素建立的地表下沉系数BP预测模型有着较好的预测效果，其绝对误差最小值为3.954%，最大值仅为-6.918%，平均相对误差为7.179%。分析表明，该模型能够应用到地表下沉系数预测，是一种可行的方法。

3)地表下沉系数的实测数据比较缺乏，导致样本数量较少，预测模型的精度在一定程度上会受样本数量的影响。随着智慧型数字化矿山的发展，更多的实测资料会得到收集利用，该模型的精度会有进一步的提升空间。