光伏发电最大功率点跟踪Boost变换器动力学特性
陶 慧,赵世彬,贾春华
(河南理工大学电气工程与自动化学院,焦作 454000)
光伏发电是利用太阳能电池的光生效应将太阳能转化为电能的一种发电形式[1]。为了提高光伏电池的转换效率,需要采用最大功率点跟踪MPPT(maximum power point tracking)技术。目前一般采用Boost变换器作为MPPT控制器,通过控制开关管通断,调节其占空比,使光伏电池稳定工作在最大功率点[2]。
对于光伏发电Boost变换器的研究,主要集中在对MPPT算法的改进。传统MPPT算法主要有恒定电压法、电导增量法和扰动观察法[3-4]。文献[5-7]基于以上传统MPPT算法提出了变步长扰动观察法、改进型变步长电导增量法、改进型模糊控制以及粒子群优化等算法来实现光伏电池MPPT,提高了系统的响应速度和控制精度,但上述MPPT算法的数学模型比较复杂,不便于系统的非线性分析;文献[8]通过保证负载阻值和光伏电池内阻相等,为实现负载功率处于最大值提供了简单的思路,但当外界环境发生变化引起光伏电池内阻改变时,无法准确跟踪到最大功率点。本文将Boost变换器和负载结合起来,视为等效负载,控制Boost变换器开关管的通断,使光伏电池阻抗和等效负载相匹配,可以达到最大功率点跟踪的目的,而且实现简单。
作为一种典型的电力电子电路,光伏发电系统具有强非线性特性。研究其非线性动力学行为,可以确定系统的稳定工作域,提高光伏发电系统的效率和稳定性,对实际工程有重要的指导意义。文献[9]建立了电压反馈型Boost变换器PD控制下的离散模型,研究了PD控制器参数对系统稳定性的影响;文献[10]研究了电流控制型Boost变换器,发现在一定参数作用下,系统会出现倍周期分岔现象;文献[11]研究了电压模式控制Boost变换器的切分岔和阵发混沌等不稳定现象,为变换器参数的优化提供了重要指导意义;文献[12]基于离散法,建立了交错并联Boost变换器的离散映射模型,研究了电流反馈增益和电压反馈增益对系统动力学特性的影响;文献[13]推导了两级式光伏并网逆变器的状态方程,研究了前后级电路内部参数的取值对系统非线性行为的影响,避免了混沌引起的稳定性和鲁棒性变差等问题,为实际光伏逆变器的设计提供了重要的理论依据。但目前对Boost电路和光伏发电系统非线性的研究,没有考虑最大功率点跟踪的控制要求。此外,光伏电池结构复杂,等效数学模型主要有单二极管模型、双二极管模型和3个二极管模型等[14]。但多数学者对光伏发电系统进行非线性研究时,直接将光伏电池等效为一个电动势,忽略了光伏电池内部参数对其工作特性的影响。为了反映光伏电池的真实特性,本文将光伏电池模型等效为直流电压源。该模型便于分析当外界环境变化引起光伏电池内阻改变时其内阻对系统的影响。
本文从非线性动力学角度出发,来揭示光伏发电MPPT Boost变换器的动力学特性。首先给出了光伏电池的等效电压源模型和基于阻抗匹配的MPPT原理,分析系统的工作原理并建立其数学模型。然后进行数值仿真,利用分岔图、时域波形以及相图深入研究系统的非线性行为,并根据系统状态平均方程的雅可比矩阵特征值,对系统稳定性进行理论分析,确定系统各参数的稳定域和稳定边界。最后在Matlab/Simulink环境下进行仿真验证。
1 光伏电池等效模型及MPPT实现
1.1 光伏电池模型
光伏电池单二极管电路模型[14]及其等效模型如图1所示。

图1 光伏电池电路模型Fig.1 Circuit models of photovoltaic cell
实际工程中,单个光伏电池产生的电压很小,因此需要许多光伏电池通过串、并联组合得到期望的光伏电池阵列,其输出特性方程为

式中:I、Iph和ID分别为光伏电池的输出电流、光电流和二极管反向饱和电流;upv为光伏电池输出电压;ns和np分别为光伏电池串联和并联的个数;q为电子的电荷量;A为p-n结常数;K为玻尔兹曼常数;T为光伏电池温度;Rsh为光伏电池并联电阻;Rs为光伏电池串联电阻。
由式(1)可知,光伏电池I-U特性方程是一个非线性超越函数。在研究光伏发电系统的动力学特性时,若采用单二极管模型作为光伏电池等效模型,不便于对系统的状态微分方程进行求解。本文根据已知的光伏电池开路电压和短路电流等参数,利用戴维南定理,将其等效为电动势和内阻串联,如图1(b)所示,能更准确地反映光伏电池的真实特性,并且便于从非线性角度分析光伏发电系统的动力学特性。其中等效电动势E为光伏电池开路电压;Req为光伏电池等效电阻,可由开路电压和短路电流求得。
1.2 光伏电池MPPT
为了提高光伏电池的转换效率,最大限度地将太阳能转化为电能,应该使光伏电池工作在最大功率点处。文献[8]本着负载电阻和光伏阵列等效内阻相等的原则进行负载匹配,使光伏电池工作在最大输出状态。其简化线性电路如图2所示。
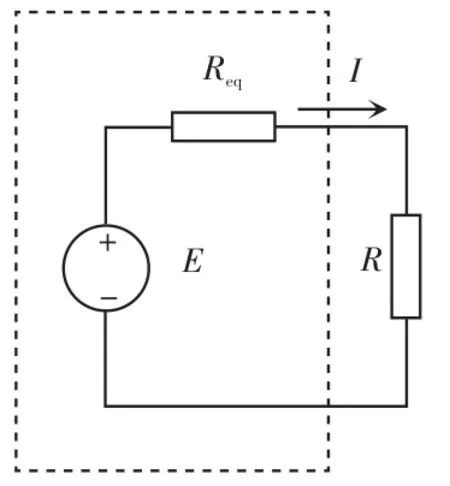
图2 简单线性电路Fig.2 Simplified linear circuit
图2中,R为负载,其消耗的功率可表示为

式(2)对负载R求导,可得

2 系统模型与工作原理
光伏发电MPPT Boost变换器原理如图3所示。系统分为主电路和控制系统两部分,其中:主电路包括等效电动势E、光伏电池等效内阻Req、滤波电容Cf、Boost电路以及阻性负载R;控制系统包含光伏电池输出电压外环和电感电流内环。电压外环采用比例积分控制,目的是控制光伏电池输出电压upv稳定在E/2,使光伏电池可以稳定工作在最大功率点处;电流内环采用比例控制,通过反馈电感电流来提高系统的动态响应特性。工作原理如下:首先,将光伏电池输出电压upv与参考电压Uref比较,通过电压外环控制器得到电流参考信号iref;然后将iref和电感电流iL经电流内环控制器运算后得到控制电压ucon,经峰值为3的锯齿波调制后形成PWM信号,控制开关管S的通断。

图3 系统原理Fig.3 Schematic of system
图3中,锯齿波信号为

式中:VL和VH分别为锯齿波信号的下饱和边界值和上饱和边界值;t为时间;T为开关周期。
控制电压ucon可表示为
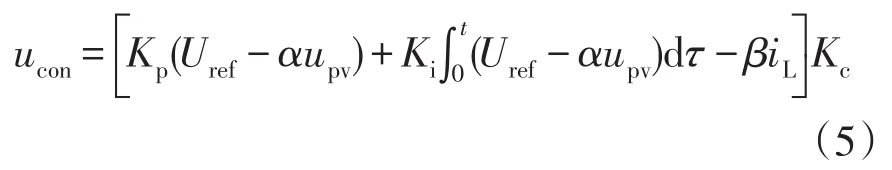
式中:Kp为电压外环比例系数;Ki为电压外环积分系数;Kc为电流内环比例系数;α为电压反馈系数;β为电流反馈系数;iL为电感电流;Uref为参考电压。
通过比较ucon和vramp可以确定开关管的运行状态。当vramp>ucon时,S=1,开关管S导通,D关断;当vramp<ucon时,S=0,开关管S关断,D导通。
每个状态对应的状态方程表示为


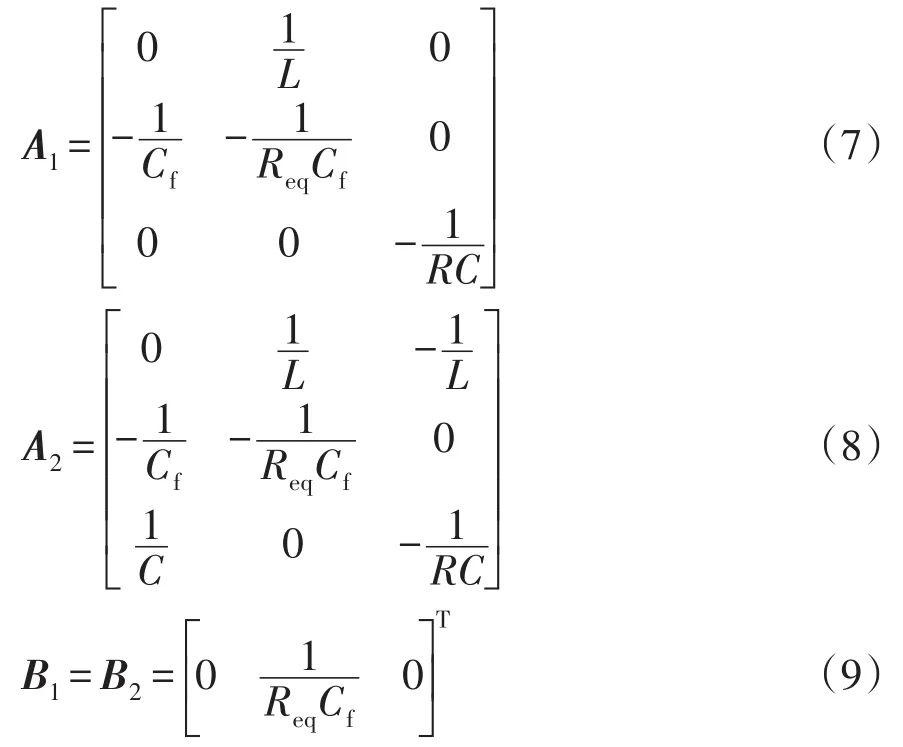
式中:L为Boost电路电感;C为Boost电路电容;Cf为滤波电容。
结合式(5)~式(9),可得整个电路系统状态方程为

3 数值仿真研究
基于式(10)得到的系统状态微分方程,利用迭代法对系统进行数值仿真研究。数值仿真采用的电路默认参数如表1所示。

表1 数值仿真采用的电路默认参数Tab.1 Default circuit parameters used in numerical simulation
目前,辨识混沌运动的方法主要有:直接观测法、庞加莱截面法、相图法、分岔图法以及Lyapunov指数法。其中,分岔图是以系统的某一参数为横坐标、某一状态变量为纵坐标,通过数值仿真迭代计算方程得到的,可以直观地反映系统随参数变化的动力学行为。系统周期运动状态与分岔图中点的个数相对应,当分岔图中存在无数个位置不重复的点时,则说明系统处于混沌状态。
本文通过分岔图法,分别研究当光伏电池等效内阻Req、电动势E、电压外环比例系数Kp以及滤波电容Cf改变时对系统的稳定性的影响。
3.1 以Req为分岔参数
光伏电池等效内阻的变化会影响其输出电压,首先研究光伏电池内阻变化时系统的非线性行为。图4给出了当其他参数取默认值,系统随Req变化时光伏电池输出电压upv的分岔图。通过观察分岔图可以看出:当Req<0.656 Ω时,系统处于混沌状态;当Req>0.656 Ω时,系统稳定运行;约在Req=0.656 Ω时,系统处于临界稳定状态。

图4 系统随Req变化时upv的分岔图Fig.4 Bifurcation diagram ofupvupv asReqvaries
由文献[14]可知:当环境温度不变时,光照强度与Req成反比,与光伏电池最大输出功率成正比;当光照强度不变时,Req和最大输出功率均会随着环境温度的增大而减小。由此可见,当外界环境温度或光照强度增大使Req小于其临界稳定值时,系统处于混沌状态;但当环境温度降低时,不仅会增大光伏电池最大输出功率,同时还能保证内阻Req在其稳定域内工作。
3.2 以E为分岔参数
考虑到Boost变换器的输入电压是由光伏电池产生的,等效电动势E随环境温度和光照强度等因素的改变而发生较大范围的变化。以E为分岔参数,研究upv的动力学行为,对实际工程设计也有重要意义。图5给出了参数E变化范围为10~30 V时upv的分岔图。可见,当E<13.96 V时,系统稳定运行在周期1;在13.96 V<E<17.68 V时,系统运行在不稳定状态;约在E=17.68 V处,系统发生了由混沌状态到稳定状态的转变。因此,在实际工程中,为保证系统稳定运行,E的取值应大于17.68 V。

图5 系统随E变化时upv的分岔图Fig.5 Bifurcation diagram ofupvas E varies
3.3 以Kp为分岔参数
实际工程中,控制环节的电路参数对系统的非线性动力学特性有很大的影响,选取合适的控制参数,有助于系统的稳定运行。图6给出了当其他电路参数不变、系统随电压外环比例系数Kp变化时光伏电池输出电压upv的分岔图。可见,当Kp>0.7时,系统稳定运行,光伏电池输出电压稳定在12 V;当Kp<0.7时,系统失去稳定,出现混沌现象。

图6 系统随KP变化时upv的分岔图Fig.6 Bifurcation diagram ofupvasKPvaries
3.4 以Cf为分岔参数
滤波参数也会对系统的动力学特性产生影响,以滤波电容Cf为参数的分岔图如图7所示。可以看出,大约在Cf=24.6 μF时,系统由稳定状态进入混沌状态,并且在随后的参数变化区域内,周期态与混沌态小范围交替出现。由此,在实际工程设计中,为避免系统出现混沌,Cf需要在0~24.6 μF内取值。

图7 系统随Cf变化时upv的分岔图Fig.7 Bifurcation diagram ofupvasCfvaries
4 稳定性分析
本文采用雅可比矩阵法对系统的稳定性进行理论分析。首先求解系统的平衡点,然后针对系统状态方程系数矩阵含时变参数的问题,在平衡点处对系统的状态平均方程做线性化处理,最后根据雅可比矩阵的特征值对系统进行稳定性分析。
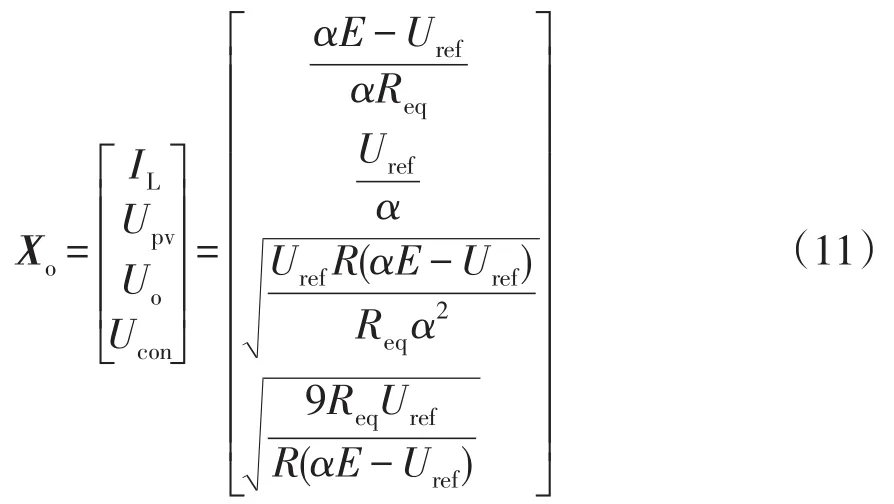
根据式(10)可得系统的状态平均方程为

在平衡点Xo处,对式(12)进行线性化处理,可得到系统的线性化方程为

因此,式(13)的雅可比矩阵为

求雅可比矩阵特征值的方程为

基于式(14)和式(15),可以准确计算出系统在平衡点处雅可比矩阵特征值随参数Req、E、Kp及Cf变化的轨迹,确定分岔点位置。为了保证系统在临界稳定时,雅可比矩阵特征值尽可能接近虚轴,本文对各参数的取值精确到小数点后4位,取雅可比矩阵特征值最接近虚轴时对应的参数值为其临界稳定值,结果如表2~表5所示。

表2 雅可比矩阵特征值随参数Req变化的情形Tab.2 Eigenvalues of Jacobian matrix asReqvaries

表3 雅可比矩阵特征值随参数E变化的情形Tab.3 Eigenvalues of Jacobian matrix as E varies

表4 雅可比矩阵特征值随参数Kp变化的情形Tab.4 Eigenvalues of Jacobian matrix asKpvaries

表5 雅可比矩阵特征值随参数Cf变化的情形Tab.5 Eigenvalues of Jacobian matrix asCfvaries
由表2可知:以光伏电池等效内阻Req为分岔参数,当Req<0.656 1 Ω时,系统的雅可比矩阵特征值在复平面右半部分,说明此时系统处于不稳定状态;当Req=0.656 1 Ω时,雅可比矩阵特征值穿越虚轴,进入复平面左半部分,系统处于临界稳定状态;当Req>0.656 1 Ω时,系统的雅可比矩阵特征值全部位于复平面左半部分,说明此时系统稳定运行。与图4结果吻合。
由表3可知:以等效电动势E为分岔参数,当E<13.960 3或E>17.679 6时,系统的雅可比矩阵特征值在复平面左半部分,说明此时系统处于稳定状态;当13.960 3<E<17.679 6时,系统的雅可比矩阵特征值全部位于复平面右半部分,说明此时系统处于混沌状态;当E=13.960 3或E=17.679 6时,系统处于临界稳定状态。结果与图5相互照应。
由表4可知:以电压环比例系数Kp为分岔参数,当Kp<0.724 3时,系统处于混沌状态;继续增大Kp,当Kp=0.724 3时,系统临界稳定;当Kp>0.724 3时,系统的雅可比矩阵特征值处于复平面左半部分,说明系统稳定运行。与图6结果一致。
由表5可知:以滤波电容Cf为分岔参数,当Cf=24.595 5 μF时,雅可比矩阵特征值穿越虚轴进入右半平面,系统处于临界稳定状态;当Cf>24.595 5 μF时,雅可比矩阵特征值处于复平面右半部分,系统处于混沌状态;当Cf<24.595 5 μF时,雅可比矩阵特征值处于复平面左半部分,系统稳定运行。结果与图7相照应。
对于系统的设计而言,能够确定系统失稳的边界参数是非常重要的。由于等效电动势E和内阻Req对光伏电池输出电压有很大的影响。因此,图8给出了E-Req构成的二维参数平面上的稳定性边界,分别基于理论分析和数值仿真得到的稳定性边界进行对比,以便于协助工程师选择合适的输入参数,避免系统出现混沌现象。
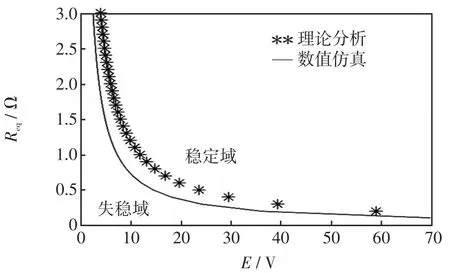
图8 系统在平面上的稳定性边界Fig.8 Stability boundary on E-Req plane
5 Matlab/Simulink仿真验证
时域波形是某一状态变量随时间变化的历程,相图是在相空间下系统不同状态变量间的关系,二者通过记录系统的运动轨迹,直接反映系统的当前运行状态。从这两个角度出发,对系统的主电路及控制电路进行仿真验证,系统仿真参数如表1所示。
系统默认参数运行时upv和iL的时域波形如图9(a)所示,可见,upv、iL分别稳定在12 V、5 A,光伏电池的输出功率达到最大值60 W,实现了系统的控制目标。去掉前20 000个周期之后,每隔一个开关周期对iL和upv进行一次采样,可得二者的相图如图9(b)所示,采样点均重合在一个位置,此时相图为一个点,说明系统稳定运行于周期1。

图9 系统默认参数运行的时域波形及相图Fig.9 Time-domain waveforms and phase trajectory during system operation with default parameters
保持其他参数不变,图10给出了Req=0.6 Ω时upv和iL的时域波形及其相图。由图10(a)可以看出,在某些开关周期内电感电流下降到0,说明系统在CCM和DCM模式下交替运行。iL和upv的相图如图10(b)所示,相点的移动轨迹为一条斜线,二者呈现反方向大幅度的变化,说明系统处于混沌状态。
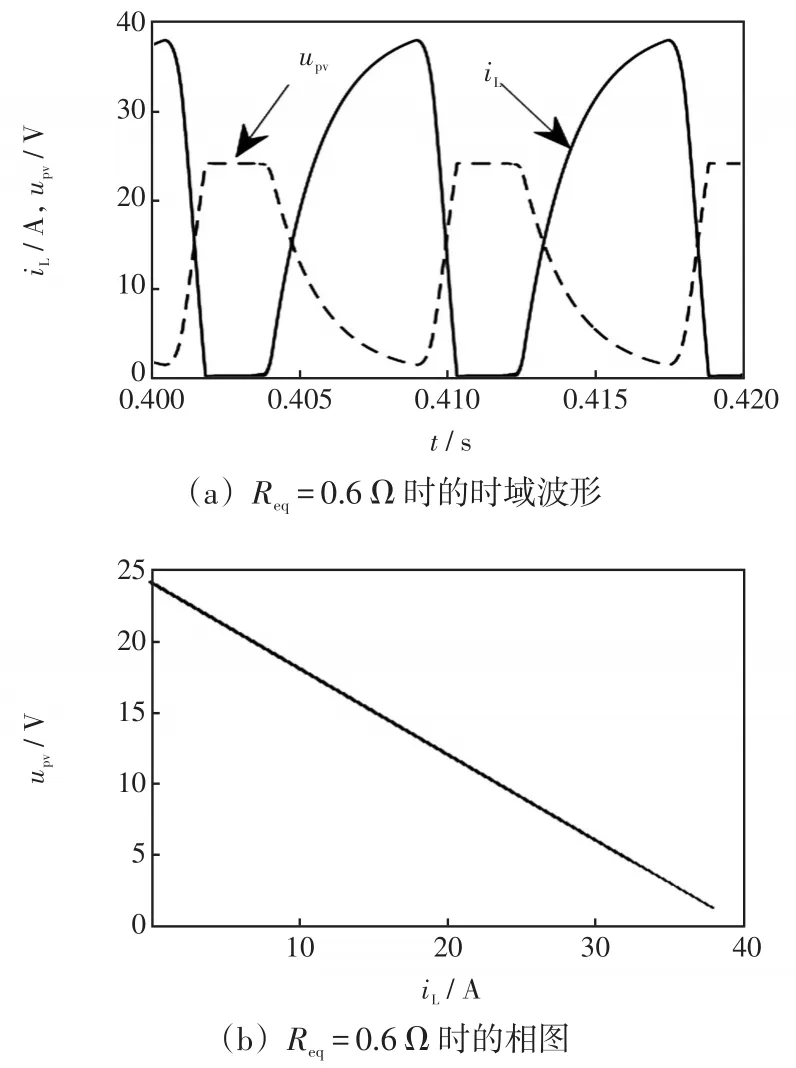
图10 Req=0.6 Ω时的时域波形及相图Fig.10 Time-domain waveforms and phase trajectory withReq=0.6 Ω
保持其他参数不变,图11给出了E=16 V时,upv和iL的时域波形及其相图。由图11(a)可以看出,upv和iL的变化幅度分别为4.06 V和3.35 A。如图11(b)所示,此时二者的相图由无数个位置不重合的闭合曲线组成,说明系统处于混沌状态。

图11 E=16 V时的时域波形及相图Fig.11 Time-domain waveforms and phase trajectory withE=16 V
只改变电压外环比例系数Kp,当Kp=0.7时upv和iL的时域波形及其相图如图12所示。由图12(a)可知,upv和iL的变化幅度分别为20.06 V和8.38 A,此时二者的相图为一条闭合且两端无规则变化的曲线,此时系统处于不稳定状态,如图12(b)所示。

图12 Kp=0.7时的时域波形及相图Fig.12 Time-domain waveforms and phase trajectory withKp=0.7
当保持其他参数不变、滤波电容Cf=24.6 μF时,系统开始出现混沌现象。图13给出了Cf=100 μF时upv和iL的时域波形及其相图。由图13(a)可知,upv和iL的变化幅度分别为8.58 V和7.702 A。此时二者的相图由无数个位置不重合的闭合曲线组成,说明系统处于混沌状态,如图13(b)所示。

图13 Cf=100 μF时的时域波形及相图Fig.13 Time-domain waveforms and phase trajectory withCf=100 μF
通过观察系统在不同参数下运行时upv和iL的时域波形及其相图可知:当系统稳定运行时,upv和iL的波形为一条直线,二者的相图由无数个位置重合的点组成;当系统处于混沌状态时,upv和iL的波形出现大幅度变化,二者的相图也呈现出各种不规则的图形。
6 结 论
(1)光伏电池内阻对系统的动力学特性产生影响,为更准确反映其真实特性,将光伏电池等效为电动势和等效内阻串联。基于阻抗匹配原则确定了系统结构,通过控制光伏电池输出电压在E/2处,实现负载功率最大。
(2)通过数值仿真确定了系统的输入参数Req和E、控制参数Kp、滤波参数Cf的稳定域以及E-Req构成的二维参数平面上的稳定性边界。采用雅可比矩阵法对系统的稳定性进行理论分析,与数值仿真结果相吻合。当外界环境温度或光照强度增大到一定条件时,系统会因为Req小于其临界稳定值而出现混沌现象。当环境温度降低时,光伏电池的最大输出功率会变大,同时也能保证Req在其稳定域内工作。研究结果为光伏发电MPPT Boost变换器的实际设计及调试提供了重要的理论依据。

