地震灾害下的电气耦合系统韧性评估
吴 彬,高军彦,班 全,赵玉新
(国网天津市电力公司电力科学研究院,天津 300384)
近年来,地震灾害在全球范围内愈来愈频繁,强度愈来愈高。2008年,中国汶川发生了8.0级地震,导致四川省电网瞬时损失负荷31.8%,供气系统同样受损严重,仅都江堰市燃气管道重建长度就达150 km[1-2]。2011年,日本3·11地震达到9.0级,致使日本仙台以及附近岛屿发生大范围停电事故,燃气管道破裂共计84处,燃气泄露引发多处火灾[3]。另一方面,为了实现能源系统的清洁化转型,化石能源发电将逐渐被天然气发电所取代,电力系统与天然气系统的耦合程度日益加深[4]。在地震灾害冲击下,电气耦合系统可能发生元件故障,严重时会导致停电停气事故。因此,有必要对地震带来的巨大影响和损失展开分析,研究地震灾害下电气耦合系统的韧性评估方法。
韧性描述了系统抵御极端灾害冲击并从中快速恢复的能力[5-6],它包括了4个关键属性:鲁棒性(robustness)、冗余性(redundancy)、机敏性(resourcefulness)和快速性(rapidity),记为“4R”属性[7]。现有文献对韧性指标展开了大量研究。韧性三角[8]和韧性梯形[9]将韧性指标定义为系统功能损害部分与时间的积分,通过韧性的鲁棒性和快速性体现韧性“4R”属性的共同影响[10]。文献[11]指出能源输送系统应确保在面临扰动时足够坚强,因此更侧重于系统抵御极端灾害的能力;考虑到鲁棒性在输电网韧性中的主体地位,文献[12]将系统韧性指标简化为负荷损失期望。这一简化韧性指标不局限于输电网,它可以扩展到最常见的跨区级综合能源系统—电气耦合系统中。
作为灾害机理建模与能源系统分析的跨学科融合研究,各类灾害背景下的韧性评估已经成为近些年的研究热点。文献[13]参考美国大西洋盆地飓风数据库记载的历年事故,为研究区域构建了概率性灾害模型;文献[14]建立了基于序贯蒙特卡洛的时间序列模型,用以评估飓风过境期间的系统韧性水平;文献[15]提出了计及冰灾影响的韧性评估方法,分别从灾前、灾中两个阶段定位系统薄弱环节;文献[16]采用网络栅格法分别模拟了极端自然灾害下电气耦合系统受到灾害破坏的场景,分析了天然气系统对电力系统灾后恢复过程的影响;文献[17]采用组合枚举法生成潜在台风场景集,并以每个潜在灾害场景下系统负荷损失期望的加权和作为面向规划的韧性指标。
作为最常见的地质灾害之一,地震灾害能够同时打击电力系统和天然气系统,容易引发电气耦合系统的跨系统多阶故障。考虑到现有研究对地震灾害下电气耦合系统韧性评估的研究较少,本文构建了描述灾害场景不确定性的地震概率模型和描述灾害攻击影响的地震攻击模型,介绍了电气耦合系统的负荷削减优化算法,并提出了基于潜在地震场景集的韧性评估方法。所提韧性评估方法被应用于IEEE RTS79电网和14节点气网组成的电气耦合系统中,基于蒙特卡洛法求得系统级和元件级的韧性指标,前者用以判断系统韧性水平为否达标,后者则可用于指导制订韧性提升策略。
1 地震灾害建模
1.1 地震概率模型
极端灾害的发生具有不确定性,地震可能以任意震级发生在研究区域内的任意一点。针对地震灾害场景的不确定性,对地震活动特征进行建模,介绍了地震震级M和震中点(x,y)的分布函数。
1.1.1 三级潜在震源区划分方案
考虑到我国地震活动的空间多层次不均匀性,现行第五代《中国地震动参数区划图》[18]采用了地震统计区—背景源—构造源三级潜在震源区划分方案。以某一地震统计区为研究区域,该划分方案从地震统计区内划分背景源以表现不同背景地震活动特征,并在各个背景源中划分出沿活动断层分布的构造源。
图1中给出了三级潜在震源区划分方案的示意,其中,地震统计区划分为构造源A、构造源B、背景源C和背景源D。设Mu为地震统计区的震级上限,Mu,A、Mu,B、Mu,C和Mu,D分别为潜在震源区A、B、C和D的震级上限。构造源的震级上限应高于其所属的背景源,在图1中体现为Mu,A>Mu,C和Mu,B>Mu,D;地震统计区震级上限应等于它包含所有构造源的最高震级上限,体现为Mu=Mu,A。起算震级M0表示对设施产生威胁的最低震级,通常取作4.0。对地震统计区发生的地震场景而言,震级可行域为[M0,Mu],震中点的可行域为统计区全域。

图1 三级潜在震源区划分方案Fig.1 Three-level delineation scheme for potential earthquake sources
1.1.2 地震场景生成
为便于分析,本文假定震级和震中点为能够全面描述某一特定地震场景的最小参数组。潜在地震场景的生成本质上为此参数组的生成,且各地震场景的发生概率与地震震级和震中点坐标的分布密切相关。
将地震统计区内所有地震按震级划分为数个震级档,设各震级档档距均为ΔM,则震级的分布函数[19]为

式中:Mj为第j个震级档的中心值,Mj=[Mj-ΔM/2,Mj+ΔM/2];ωr(Mj)为地震统计区内发生的地震属于第j档的概率;β=bln10,其中b为地震统计区G-R公式中的系数;Mu和M0分别为地震统计区的震级上限和起算震级;exp为指数函数;sh为双曲正弦函数。
背景源和构造源可以统称为狭义的潜在震源区,简记作潜源区。采用网格取点法枚举得到潜在震中点后,统计区内第j档地震的震中点分布函数可表示为

式中:ωr(( x,y)|Mj)为第j档地震发生于第i个潜源区的网格枚举点(x,y)的概率;ci为属于第i个潜源区的枚举震中点个数;Ns为地震统计区内潜源区的总个数;αi为第i个潜源区的地震活动权重[20],可表示为

式中,Mu,i为第i个潜源区的震级上限。
以各个潜源区的震级上限为分区界限,震级可行域可以划分为数个区间,每个区间又包含着若干震级档。超出潜源区震级上限的地震被认为不会发生在该潜源区,因此震中点的分布与地震震级存在一定的关联性:不同震级区间中的震级档对应不同的潜在震中点集合。基于组合枚举的地震场景生成如图2所示,图中属于震级区间[M0,Mu,D]的震级档对应的震中点遍布整个地震统计区,而属于震级区间[Mu,B,Mu,A]的震级档对应的震中点只可能取自构造源A。

图2 基于组合枚举的地震场景生成Fig.2 Earthquake scenario generation based on combinatorial enumeration
如图2所示,将地震震级和震中点的可行域划分为多段取值区间,这些区间被逐一选择组合生成潜在地震场景集。首先枚举地震场景的震级档,然后从所枚举震级档对应的潜在震中点集合中枚举震中点坐标,生成的潜在地震场景记作e,则在已知一次地震发生的前提下此灾害场景为e的概率可表示为

场景发生概率ωe由震级分布与震中点分布求得,它可用以表述地震场景e所致系统损失在规划设计中的权重。
1.2 地震攻击模型
在一次震级、震中点已知的特定地震场景下,电气耦合系统空间上各点所承受的打击通常为不均匀的。为此,对地震攻击模式进行建模,并基于地震烈度分布构建地震灾害下的元件失效概率模型。
1.2.1 烈度分布
与关注地震自身强度的震级不同,地震烈度描述的为地震造成的破坏程度。地震波从震中点向外延传播能量,烈度随着震中距的增长而不断衰减。我国目前采用12度烈度表为烈度标准,其中地震低于6度时一般不会损坏系统设施,而烈度高于8度的情况非常少见且范围极小。因此本文只考虑地震烈度为6、7、8度的分布。
椭圆烈度衰减模型[21]将地震等烈度线视为同心同向的椭圆群,在椭圆长轴或短轴方向上各点的地震烈度I表示为

式中:r为震中距;M为地震震级;A、B、C和 r0为回归参数,且地震长、短轴有不同的回归参数。
当烈度已知时,反推式(5)可得此烈度对应等烈度线的长、短轴半径,即

等烈度线椭圆以震中点为中心,长轴方向则与距离震中点最近的活动断层走向保持一致[22]。为简化分析,本文将强度为(I±0.5)的等烈度线所包围的区域记作烈度I区,并假定烈度I区内任意一点的烈度均为I。根据椭圆的数学性质可知电气耦合系统任意一点(xd,yd)烈度为Id的充要条件,表示为
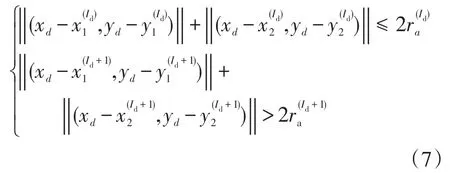
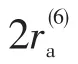

图3 地震烈度分布Fig.3 Distribution of earthquake intensity
1.2.2 元件失效概率模型
与天气灾害不同,地震对位于地表的变压器、架空输电线路和深埋地下中的燃气管道均具有较强的破坏力,以下对这三类元件的失效概率模型进行介绍。
变压器在受灾区域中为一个点拓扑模型,确定变压器地点所处的烈度区后,根据历史数据即可得到变压器基于地震烈度的失效概率pk,tr。
架空线路的构件包括输电线和输电杆塔。输电线能够通过低频振动解耦输入的地震能量,故地震下架空输电线路的失效概率主要与起支撑作用的输电杆塔有关。架空线路m的失效概率可表示为

式中:a∈m指所有属于线路m的杆塔;λa为杆塔a在地震下的失效概率,与烈度的关系见文献[23]。
燃气管道可能跨越多个地震烈度区,为此将燃气管道等分为数个元管道。元管道足够小时,其位置可以由中点表示。类比杆塔构成的架空线路,元管道构成的燃气管道n的失效概率可表示为



式中:Rf为地震震害率;ΔL为元管道长度。
至此,可得电气互联系统元件失效概率集合为

式中,pk为元件k的失效概率。
2 基于潜在地震场景集的韧性评估
地震灾害建模可以生成一个丰富的潜在地震场景集,并给出每个潜在场景的发生条件概率和元件失效概率,从而为韧性评估提供数据支撑。本节设计了基于潜在地震场景集的韧性评估方法,并将该方法应用于电气耦合系统中。
2.1 韧性指标
2.1.1 系统级与元件级韧性指标
地震灾害持续时间非常短暂,不具备时空特性。此外,受余震影响,地震灾后恢复机制极为复杂。为便于分析,本文忽略了灾后恢复过程,以负荷损失期望为韧性指标。作为跨区级能源传输系统,电气耦合系统采用此简化指标为合理的。
系统级韧性指标Rsys描述了发生一次地震灾害后的预期负荷损失,可以表示为

式中:Ne为潜在地震场景的总个数;ωi为第i个潜在场景的发生概率;Ei[Qshed]为第i个潜在场景下的电气耦合系统负荷损失期望值。指标Rsys越低,系统的韧性水平越高。
元件级韧性指标Rk描述了针对元件k的强化措施提升系统韧性的能力[25],可以表示为

2.1.2 负荷损失期望的求解
本文采用蒙特卡洛模拟MCS(Monte Carlo simulation)法求解负荷损失期望Ei[Qshed],首先为电气耦合系统的元件k生成一个[0,1]区间内的随机数uk,然后将其与元件k的失效概率pk进行对比,从而模拟元件k的运行状态,描述为

式中,sk为元件k的运行状态,其为1时表示元件正常运行,其为0时表示元件失效。
在模拟完所有元件的运行状态后,MCS就抽样生成了一次故障状态。抽取足够多的故障状态后,所有状态下系统负荷削减量的平均值即为MCS法的计算结果,即

式中:N为MCS法抽取的故障状态总数;Qshed,s为第s个样本故障状态下电气耦合系统的最优负荷削减量。
2.2 电气耦合系统负荷削减优化算法
为求得韧性指标,需要计算MCS抽取故障状态下电气耦合系统的最优负荷削减量,为此对电气耦合系统负荷削减优化算法进行介绍。
2.2.1 解耦优化流程
燃气发电厂比传统火电厂更低碳环保,随着“双碳”目标的提出,其应用热度与日俱增。为便于分析,本文只考虑了燃气发电厂一种耦合设施。在电力子系统中,燃气发电厂扮演着“源”的角色,而在天然气子系统中,燃气发电厂则扮演了“荷”的身份。
本文在解耦框架下求解电气耦合系统的最优负荷削减量。解耦的思路为对电力子系统和天然气子系统进行交替优化,直至天然气子系统可以满足燃气发电厂的供气需求,即燃气电厂的供气负荷削减量小于收敛阈值时,优化过程结束。电气耦合系统的解耦优化流程如图4所示。

图4 解耦优化流程Fig.4 Flow chart of decoupling optimization
具体步骤描述如下。
步骤1 对故障状态下的电力子系统进行负荷削减优化计算,求得燃气发电厂的出力Pu。
步骤2 根据燃气发电厂的耗量特性方程Gu=ηPu计算天然气系统与燃气发电厂相连节点的供气负荷Gu。其中η为耗气转化参数,即燃气发电厂单位出力所需供气量。
步骤3 对故障状态下的天然气子系统进行负荷削减优化计算,得到燃气电厂的供气负荷削减量Gs。
步骤4 若Gs≤ε,认为天然气系统能够满足电力系统供气需求,跳到步骤5;反之,修改燃气发电厂出力上限Pu,max为(Gu-Gs)/η,返回步骤1。ε为收敛阈值,应取为足够小的正数。
步骤5 将系统气负荷削减量折算后与电负荷削减量相加,从而得到总的负荷削减量,即

式中:Qshed为电气耦合系统的最优负荷削减量;Pshed为电负荷削减量,单位为MW;Gshed为气负荷削减量,单位为m3/h;q为天然气低热值,可取为35.59 MJ/m3。
2.2.2 电负荷削减优化模型
与直流潮流模型不同,交流潮流模型能够充分考虑各种运行约束,为对实际系统的真实反映。因此,本文基于交流潮流模型构建电力子系统的负荷削减优化模型,以发电厂出力为优化变量,以负荷削减总量最少为目标,其目标函数和约束条件分别为

式中:Pshed为各节点电负荷削减量之和;ϕ为电力子系统的节点集合;Pdi为节点i的有功负荷;Psi为节点i的有功负荷切除量;Si为节点i的节点注入复功率;Yij为节点导纳矩阵中第i行第j列的元素;conj(·)表示取共轭;Pij和Pij,max分别为线路ij的有功潮流和潮流上限;U̇i和U̇j分别为节点i和节点j的电压相量;Ui为节点i的电压幅值;Ui,max和Ui,min分别为节点i电压幅值的上、下限;Pui和Qui分别为节点i处发电厂的有功、无功出力;Pui,max和Pui,min分别为节点i处发电厂有功出力的上、下限;Qui,max和Qui,min分别为节点i处发电厂无功出力的上、下限。该优化模型可以利用Matpower工具包进行求解。
2.2.3 气负荷削减优化模型
燃气管道的天然气流量与两端气压满足Weymouth方程约束,即

式中:fij为燃气管道ij的流量;cij为管道参数;πi和πj分别为管道入口和出口节点的气压。


式中:fij,U和fij,L分别为管道流量fij的上、下限;Nsg为fij取值区间的分段个数;l为各取值段序号;δl和φl为分段线性化方法引入的变量。
针对式(25)右侧中的非线性项与绝对值符号,采用线性化处理为

式中:Vi和Vj分别为节点i和节点j的气压平方;Tij为管道ij两端节点气压平方差的绝对值;Vi,max和Vi,min分别为节点i气压平方的上、下限;Vj,max和Vj,min分别为节点j气压平方的上、下限;gij为描述管道ij天然气流向的0/1型变量(流向为正时gij为1;流向为负时gij为0)。
压缩机耗能较少,考虑到压缩机耗量方程非线性程度较高,本文假定压缩机耗气量或耗电量为0。至此,气网优化模型被简化为一个混合整数线性模型,该模型的目标函数与约束条件为
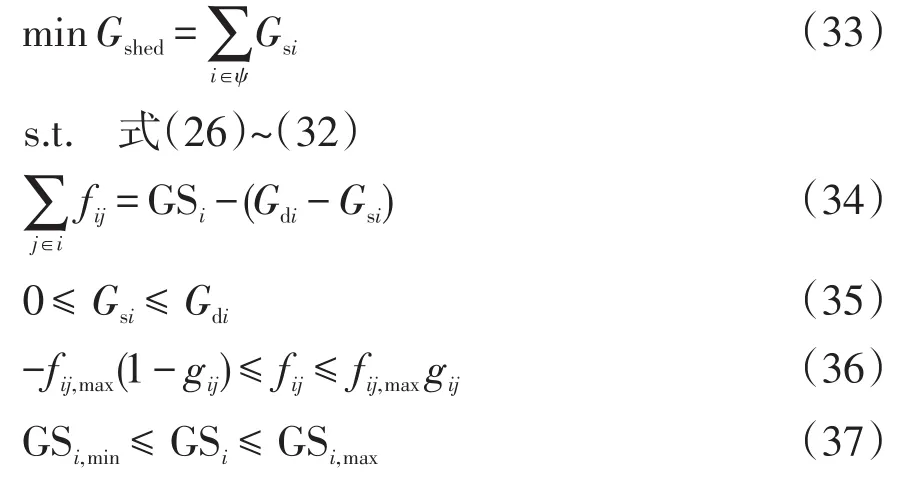

式中:Gshed为各节点气负荷削减量之和;ψ为天然气子系统节点集;fij,max为燃气管道ij的流量上限;GSi为节点i处的气源出力;GSi,max和GSi,min为节点i处气源出力的上、下限;Gdi为节点i的气负荷;Gsi为节点i的气负荷切除值;Vc,in和Vc,out分别为压缩机c入节点和出节点气压的平方;kc,max和kc,min分别为压缩比的上、下限;gc为表征压缩机c运行状态的0/1型变量(压缩机开机时gc为1;压缩机关机时gc为0);M为大M法中的常数,设置为极大正数。
式(34)为天然气节点平衡方程,即节点i的流入流量与流出流量应保持一致;式(39)~式(40)为大M法约束,其中式(39)表明压缩机停机时出口压力应等于入口压力,式(40)则表示压缩机c开机时出口压力与入口压力之比应位于区间[kc,min,kc,max]中。
气负荷削减优化模型作为一个混合整数线性规划问题,可以采用商业求解器Cplex进行求解。
2.3 计及地震灾害的电气耦合系统韧性评估框架及流程
为满足规划需求,韧性评估需要综合考虑电气耦合系统在各种潜在地震场景下的韧性表现。图5为计及地震灾害的电气耦合系统韧性评估框架的示意,其中地震概率模型依据震级、震中点分布对地震场景不确定性进行描述,地震攻击模型则围绕地震烈度分布对灾害攻击模式进行描述。
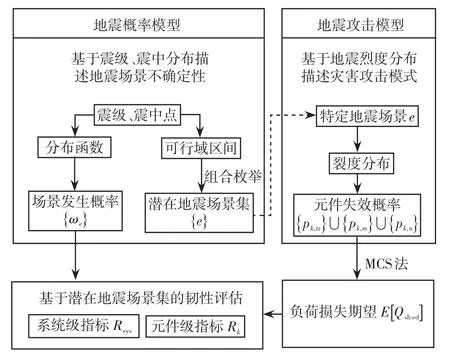
图5 地震灾害下电气耦合系统的韧性评估框架Fig.5 Resilience assessment framework for integrated electricity-gas system under earthquake disaster
在计算基于潜在地震场景集的韧性指标时,地震概率模型和地震攻击模型分别提供了各潜在场景的发生概率{ωe}和该场景下电气耦合系统各类元件的失效概率。参考图5,基于潜在地震场景集的韧性评估流程包括以下步骤:
步骤1 将地震震级和震中点的可行域划分为多个取值区间,对这些区间组合枚举得到潜在地震场景集{e},并根据式(1)~式(4)计算各潜在场景的发生概率;
步骤2 逐一分析各潜在地震场景给电气耦合系统带来的冲击,由烈度椭圆衰减模型式(5)~式(6)确定烈度分布,并基于式(7)判断各点所处烈度区,进而求得特定地震场景e下所有元件的失效概率;
步骤3 应用MCS法式(14)~式(15)计算所有潜在地震场景下的系统负荷损失期望E[Qshed],抽取故障状态所需元件失效概率由步骤2提供,各故障状态下的最优负荷削减值由第2.2节介绍的电气耦合系统负荷削减优化算法求得;
步骤4 基于式(12)计算系统级韧性指标Rsys,评估电气耦合系统韧性为否达标;基于式(13)计算元件级韧性指标Rk,用以指导制订韧性提升方案。式(12)中的ωi和E[Qshed]分别由步骤1和步骤3提供。
3 算例分析
3.1 算例介绍
本文将基于潜在地震场景集的韧性评估方法应用于电气耦合测试系统中,该算例系统由IEEE RTS79节点电力系统[27]和14节点天然气系统组成。电气耦合测试系统拓扑如图6所示,电气耦合测试系统中建有4座燃气发电厂。位于电网节点2、13、15、21的燃气发电厂分别由气网节点14、7、8、2供气。

图6 电气耦合测试系统拓扑Fig.6 Topology of integrated electricity-gas test system
电气耦合测试系统共包括33条架空输电线路、5台变压器和12条燃气管道,耦合系统中各元件编号见表1,表中P代表电力系统节点,N代表天然气系统节点。假定输电杆塔间距为300 m,气网元管道长度为500 m,算例系统其余参数如表2~表5所示,表中:η为燃气电厂的耗气转换参数,考虑到天然气发电厂启停迅速的特点,本文将燃气电厂的发电出力下限设定为0;Gd为节点气负荷;GSmax和GSmin分别为气源出力上、下限;πmax和πmin分别为节点气压上、下限;MMCFD为流量单位,表示每天百万立方英尺,节点2、7、8、14的气负荷与对应燃气电厂的出力相关。

表1 电气耦合系统元件编号Tab.1 Number of components in integrated electricitygas system

表2 燃气电厂参数Tab.2 Parameters of gas plants

表3 天然气系统节点参数Tab.3 Node parameters of natural gas system

表4 天然气系统管道参数Tab.4 Pipeline parameters of natural gas system

表5 压缩机参数Tab.5 Parameter of compressors
电气耦合测试系统被附在一个250 km×250 km的简化地震统计区上,该地区的地震模型参数如下。本文假定算例系统位于中国台湾东部地震统计区,该地区的G-R方程参数b取值为0.92,地震烈度衰减参数见表6,不同烈度下的变压器、输电杆塔失效概率和燃气管道震害率见表7。

表6 地震烈度衰减参数Tab.6 Earthquake intensity attenuation parameters

表7 基于地震烈度的元件失效概率参数Tab.7 Parameters of component failure probability based on earthquake intensity
考虑到电力子系统与天然气子系统位置相互重叠,它们在地震统计区内的空间布局在图7中分别进行展示,其中构造源A、构造源B、背景源C和背景源D的震源上限分别为8.0、7.0、6.0和5.0。值得一提的是,电网节点和气网节点的相对位置分别根据架空线路长度和燃气管道长度推导得出,且气网供气节点与燃气电厂位于同一位置。

图7 电气耦合测试系统的空间布局Fig.7 Spatial layout of integrated electricity-gas test system
3.2 潜在地震场景枚举
研究区域地震震级可行域为[4.0,8.0],假定震级档距为0.5,则共可得8个震级档。按照50 km×50 km的网格分割整个地震统计区,并以每个网格的中心点作为潜在震中点。根据构造源A、B和背景源C、D的震级上限确定各个震级档对应的潜在震中点,地震场景生成情况在图8中给出:震级档[4.0,4.5]和[4.5,5.0]的地震可能发生在任意一个潜源区内;震级档[5.0,5.5]和[5.5,6.0]的地震会在构造源A、B和背景源C中发生;震级档[6.0,6.5]和[6.5,7.0]的地震会在构造源A、B中发生;震级档[7.0,7.5]和[7.5,8.0]的地震只可能在构造源A中发生。

图8 地震场景生成示意Fig.8 Schematic of earthquake scenario generation
如图8所示,从低到高枚举震级档,并将震级档与对应的潜在震中点进行组合,共生成2×25+2×19+2×7+2×3=108个潜在地震场景。应用地震概率模型可以计算各地震场景的发生概率,以描述该场景下系统负荷损失的权重;应用地震攻击模型可以求得各地震场景下电气耦合系统元件失效概率,以结合MCS法计算该场景下的负荷损失期望。
3.3 韧性评估结果
3.3.1 潜在地震场景影响分析
本文采用MCS法分别计算各个潜在地震场景下电气耦合系统的负荷损失期望值。为确保计算效率,假定方差系数COV<0.05时MCS法计算收敛。
以场景发生概率为各个潜在地震场景负荷损失的权重,可定义第i个潜在地震场景的影响为PiEi[Qshed],它也体现了该场景下电气耦合系统的韧性表现。所有潜在地震场景的影响如图9所示,可以看到各场景的影响差别明显,部分场景影响极高。
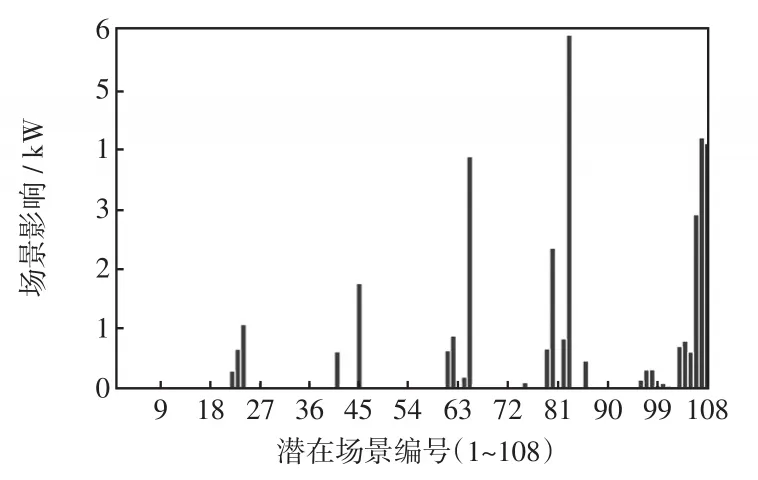
图9 潜在地震场景的影响Fig.9 Influence of potential earthquake scenarios
表8中给出了影响力前六的潜在地震场景的震级档及震中点坐标,对这些场景的空间分布描述如图10所示。发生在点[175 km,75 km]、震级档为5.5~6.0的地震具有最高的影响,一方面是因为该地震场景位于电气耦合系统的中心区域,系统所有元件均为高烈度区所覆盖;另一方面,该场景震级较低,发生概率相对较高。综合分析可知,震级上限最高的构造源A和背景源C内位于电气耦合系统中心的区域发生的地震场景影响最高。系统管理人员有必要提前做好高影响灾害场景的预案,从而有效提高不确定性地震场景下的系统韧性。

表8 高影响地震场景Tab.8 High-impact earthquake scenarios

图10 高影响地震场景空间分布Fig.10 Spatial distribution of high-impact earthquake scenarios
3.3.2 韧性指标分析
依据所提基于潜在地震场景集的韧性评估方法,可以分别求出系统级和元件级的韧性指标。系统级指标和最高的3个元件级指标如表9所示,其中元件级指标下标对应各元件编号,占比则表示该元件级指标占系统级指标的百分比。

表9 基于潜在地震场景集的韧性指标Tab.9 Resilience indices based on potential earthquake scenario set
在系统级韧性指标未达标时,规划人员需要采用元件强化方案提高系统的韧性水平。本文选择增设冗余作为元件强化措施,并假定强化元件个数限制为3。考虑到元件级指标一定程度上反映了元件的强化优先级,本文基于表1选择元件27、47、10作为一组目标强化元件,并随机抽取4组元件作为对照,分别对应方案1~5。表10给出了这5个元件强化方案的应用效果,其中ΔRsys表示系统级韧性指标的下降百分比,用以量化表示韧性提升效果。方案1的韧性提升效果远大于方案2~4,这体现了基于元件级指标排序制订元件强化方案的可行性与有效性。

表10 韧性提升效果对比Tab.10 Comparison of resilience improvement effect
4 结 语
本文提出了基于潜在地震场景集的韧性评估方法,以综合分析地震灾害给电气耦合系统带来的影响。首先,针对地震场景的不确定性构建地震概率模型,针对地震攻击机理构建地震攻击模型,从而生成潜在地震场景集,并求得各场景的发生概率及元件失效概率。然后,构建了地震灾害下的韧性评估框架,介绍了电气耦合系统负荷削减优化算法,并基于MCS法计算系统级和元件级的韧性指标。最后,对附在地震统计区上的电气耦合测试系统进行韧性评估,验证了所提韧性评估方法的可行性,评估结果可以对规划人员制订灾害预案和韧性提升方法提供参考。

