考虑设备部分负荷性能函数拟合误差的区域综合能源系统鲁棒优化调度
刘科明,黄婧杰,杨洪明,周任军
(湖南省清洁能源与智能电网协同创新中心(长沙理工大学),长沙 410114)
区域综合能源系统RIES(regional integrated energy system)是能源互联网的重要物理载体之一[1],是实现多能互补、高效用能的重要方式。
建模作为RIES优化调度的基础,能让优化调度方案更为准确合理。一方面,通过细化电、气、热、氢等供能网络的数学模型能够提高优化调度的准确性[2-4];另一方面,线性能量枢纽EH(energy hub)模型的能量转换设备效率具有不确定性,计及效率不确定性的EH鲁棒调度方案可有效降低负荷需求不被满足的风险[5]。然而线性EH中能量转换设备通常为简化模型,设备效率被当作常数[6],从而降低模型复杂度提升运算效率。但实际运行时,诸如燃气轮机、燃气锅炉GB(gas boiler)等能量转化设备的效率具有明显的部分负荷性能PLP(part load performance)[7-8],即当设备不在额定状况下运行时,其效率随负载率的变化而改变。多数能量转换设备的效率随负载率下降而降低,例如燃气轮机在低电负载率时的发电效率仅为满载运行的80%,甚至更低[8]。相比未考虑设备效率PLP,在考虑设备效率PLP后多能源系统运行成本的预测误差降低了13%[9]。设备效率的PLP能更精准有效地刻画设备运行特性,使RIES调度方案更准确合理[6]。所以各设备效率PLP的准确刻画对调度方案的影响是不可忽略的。
描述设备效率PLP的函数通常通过对实验数据或制造商提供的测试数据的拟合得到,而数据拟合导致拟合误差的客观存在[10]。文献[11]分别用线性函数和幂函数拟合燃气热电联产机组CHP(combined heat and power)热电比与电负载率的关系,所得曲线存在明显的拟合误差;文献[7]中分别用线性、二次函数拟合冷水机组性能系数COP(coefficient of performance)与负载率的关系,拟合数据与实际数据仍存在误差,但其并未考虑该误差。以上文献均未计及PLP函数的拟合误差,而忽略该误差可能导致负荷损失。为此,需探讨设备效率PLP函数的拟合误差对RIES优化结果产生何种影响。
对于不确定误差,解决工具有随机规划和鲁棒优化两种。随机规划通过分析历史数据获取不确定量的概率分布,物理意义明确,常被用于处理风、光等可再生能源出力预测误差[12],但由于生成大量场景或离散样本,该方法求解规模庞大,且要求分布信息完整准确;鲁棒优化可应对不确定变量分布信息未知的情形,使用不确定性集合描述不确定变量的变化范围[13],决策者在该范围内做出最坏情况下的最优计划,但由于缺乏足够的统计数据,难以获取PLP函数拟合误差的准确概率分布,故采取鲁棒优化方法刻画误差带来的不确定性更为合理。
结合上述分析,本文阐述了RIES中能量转换设备效率PLP函数及其拟合误差。针对该误差,引入盒式不确定集以刻画误差的波动范围,提出考虑设备部分负荷性能函数拟合误差的区域综合能源系统鲁棒优化模型。
1 能量转换设备效率PLP函数及其拟合误差
1.1 RIES框架
RIES将区域电网、热网等耦合到一起,从而实现多能互补,提高能源利用率。本文的RIES主要包含CHP、GB等能量转换设备和含蓄电池、储热水箱等能量存储设备,具体框架如图1所示。

图1 RIES框架Fig.1 Framework of RIES
1.2 能量转换设备效率的PLP函数
考虑到实际运行时,各能量转换设备通常在部分负荷工况下运行,先分析各能量转换设备的PLP。设备效率表示为

对于CHP机组,其发电效率的PLP可用4次多项式拟合得到[14],即


式中,kλ,n为CHP机组热电比函数的拟合系数。
GB的热效率与其热负载率的关系可用二次多项式拟合[15],即

1.3 PLP函数的拟合误差
设备效率PLP函数通常由多个数据点拟合而成,数据源自设备的制造商或者实物仿真的实测结果。但无论何种数据来源,将数据点拟合得到PLP函数均存在拟合误差。
本文以CHP热电比在不同电负载率下的性能为例,解释拟合误差的存在。引用文献[11]中Cummins公司提供的不同负载率下额定功率PN在1 000~2 000 kW范围的多个CHP机组热电比与负载率关系的数据,通过二次函数拟合,拟合结果见图2。
由图2可见,CHP机组的热电比PLP拟合函数存在明显的拟合误差,实际数据点分布在各拟合曲线的两侧。当电负载率为90%时,PN=1 100 kW的CHP机组热电比拟合值相对实际值的偏差最大,为1.56%。

图2 CHP热电比与其电负载率的拟合曲线Fig.2 Fitting curves of CHP’s heat-to-power ratio and electric load rate
对于各能量转换设备PLP函数的拟合误差,考虑到用于拟合的数据集来源、数据集容量、数据有效性等无法确定,而这些因素都对拟合误差造成影响,因此该拟合误差是难以获取准确概率分布的不确定变量。
2 考虑设备PLP函数的RIES优化模型
2.1 目标函数
本文以RIES日运行成本最低为目标。仅含电和天然气2种能量输入的RIES,其运行成本含购电成本C1和购气成本C2,目标函数为

式中:CELE,t和CNG,t分别为t时段购电分时电价和气价;PELE,t为t时段从电网购电功率;PCHP,t为t时段CHP电功率;QGB,t为t时段GB热功率;LHV为天然气低位热值,取9.7 kWh/m3;t∈T,T为调度周期。
2.2 约束条件
(1)功率平衡约束为

式中:Pc,t、Pd,t分别为t时段储电装置充、放电功率;Qc,t、Qd,t分别为t时段储热装置充、放热功率;PL,t、QL,t分别为t时段电负荷、热负荷。
(2)能量存储设备相关约束。储电、储热等储能设备具有通用的数学模型,具体表达式为

式中:Et为t时段储能设备容量;Emin、Emax分别为储能设备容量最小、最大值;ut为0-1变量,值为1时储能仅可充能,为0时仅可放能;PES,c,t和PES,d,t分别为t时段储能充和放能功率;PES,c,min和PES,c,max分别为储能最小和最大充能功率;PES,d,min和PES,d,max分别为储能最小和最大放能功率;ec、ed和eself分别为储能设备充能效率、放能效率和自耗能率;E0和ET分别为储能设备初始容量和T时段储能容量。式(10)中第1条约束确保储能设备在容量范围内,第2、3条约束限定了充放能功率范围,第4条约束为储能容量与充放能功率的关系,最后的约束保证储能调度周期性。
(3)设备出力范围约束为

式中:PELE,max为从电网购电的最大功率,规定RIES不允许向电网售电;QGB,min和QGB,max分别为GB最小和最大热功率;PCHP,min和PCHP,max分别为CHP最小和最大电功率。
整合以上目标和约束,可得到考虑设备效率PLP的RIES优化调度模型,表示为

3 考虑设备PLP函数拟合误差的RIES鲁棒优化模型
3.1 盒式集合鲁棒优化模型
考虑设备效率PLP的RIES优化调度模型中,CHP机组热电比PLP函数存在拟合误差,如不考虑该误差则可能造成负荷损失。而对该误差的计量,可采用随机规划方法的求解模型式(14)。但该拟合误差的准确概率分布难以获取,因此采用不确定集合U刻画拟合误差不确定量ξ及其变化范围,进而采用鲁棒优化方法求解。不确定集合有盒式、椭球和多面体等多种形式,其中盒式不确定集合的优势在于计算方便,能使线性优化、二阶锥规划和半正定规划等优化问题可以得到很好地解决[9]。为此,本文选择盒式不确定集刻画拟合误差及其范围,其具有的结构为

为表述清晰,给出式(14)对应的考虑设备PLP函数拟合误差的RIES鲁棒优化模型的紧凑形式,即

式中:c为目标函数式(5)的系数列向量;A(ξ)为含不确定量ξ的系数矩阵;G、H为相应约束中x的系数矩阵;a、g、h为常数列向量;x为决策变量向量,具体表达式为

式(16)的约束条件中,第1条约束对应式(9);第2条约束为不等式约束,包含式(10)的前3条约束和式(11)~式(13);第3条为等式约束,包含式(2)~式(4)、式(8)和式(10)后两条约束。
由于第1条约束中包含不确定量ξ,对式(16)模型的求解属于NP难问题,通过拉格朗日对偶可将其转化为易于求解的半定对偶模型[10]。
3.2 对偶转换及分段线性化处理
不确定量ξ使得CHP电负载率固定时的热电比并非确定数值,需将热功率平衡式(9)中的热电比转化为原PLP函数与不确定变量ξ之和,即
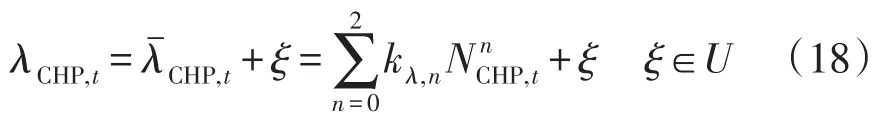
式中,λCHP,t为计及不确定量ξ后的热电比。
考虑到不确定参数的加入,将式(9)松弛[16]为

由于对所有可能的ξ∈U,都满足式(19)的约束,式(19)可等价为


式中:γ、δ分别为不确定变量ξ的上、下限约束对应的对偶变量向量,向量长度为调度周期T;γt、δt分别为ξ在t时段上下限约束对应的对偶变量。
对式(21)求导,令导数等于0,有

式中,∇ξLt(ξ,δ,γ)为Lt(ξ,δ,γ)关于ξ的导数。可见,∇ξLt(ξ,δ,γ)是与ξ无关的常数,故当ξ为零向量时原拉格朗日函数取得最小值,即

根据强对偶定理[16],有

因此,式(20)等价于


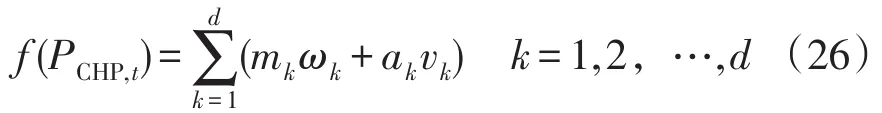
附加约束为

式中:mk为每段斜率;ak为每段的纵轴截距;ωk为引入的连续变量;bk为第k个分段点;vk为0-1变量,vk=1表示PCHP,t在第k个间隔[bk-1,bk]中。
通过拉格朗日对偶、分段线性化,最终将式(16)的鲁棒优化模型转化为优化模型,即

该模型属于混合整数半正定规划模型,可在Matlab软件中调用gurobi求解器直接求解。
4 算例分析
选取一个典型的RIES为例,该区域以电和天然气作为能量输入,通过能量转化设备传输网络的同时供给电、热负荷。区域内某日预测电负荷、热负荷以及分时电价分别如图3和图4所示。天然气价格为2元/m3,PELE,max为1 MW,RIES中各设备的详细参数及设备效率PLP函数的拟合参数如表1和表2所示。对于拟合函数的分段线性表示,考虑到线性近似精度和计算效率的均衡,分段数量d一般在30~70之间[8],故取d=50。

图3 电、热负荷Fig.3 Electric and heating loads

图4 分时电价Fig.4 Time-of-use electricity price

表1 能量转换设备参数Tab.1 Parameters of energy conversion components
仿真计算后,分析不确定参数r的不同取值对调度成本的影响,结果如图5所示。

图5 不确定参数r对调度成本的影响Fig.5 Influences of uncertain parameter r on dispatching cost
由图5可见,在基准方案下,RIES的运行成本最低,为13 050.4元;随着r的增加,成本也随之增大,即运行成本与不确定参数r呈正相关;r=0.02时鲁棒调度方案的运行成本相较于基准方案的提高了0.63%。这是因为在考虑热电比PLP函数拟合误差后,RIES需要增加能量输入的成本,以降低对随机拟合误差的敏感程度,提升调度方案的鲁棒性。
基准方案(r=0)和鲁棒方案(r=0.02)的热功率、电功率调度结果对比如图6和图7所示。

图6 两方案的热功率调度结果Fig.6 Thermal power dispatching result in two schemes

图7 两方案的电功率调度结果Fig.7 Electric power dispatching result in two schemes
从图6中可看出,鲁棒方案与基准方案有较大差距,鲁棒方案GB各时段输出热功率都略高于基准方案对应值,这是因为鲁棒方案在多数时段热电比负偏差最严重(即CHP实际热出力最低)的最恶劣场景已做出最优决策,该场景下需要通过增加GB热出力,以防止CHP实际热出力不足而引起RIES热负荷损失。
图7对比了2种方案的电功率调度情况,可见两方案电功率调度的整体差别不大,但在第6~7时段鲁棒方案下CHP输出的电功率比基准方案的少16 kW,对应的从电网购电的功率比基准方案的多16 kW。这主要是由于第6~7时段为电负荷低谷,CHP处于低负载状态,由式(2)知CHP在低电负载率时发电效率较低导致发电成本高,而图6显示GB在该时段处于高热负载率状态,产热效率高。因此相比于用CHP热电联供,在第6~7时段通过从电网以谷价购电、使用GB高效制热分别供应电、热负荷的方式的总用能成本更低,从而在鲁棒方案下该时段从电网购电的功率有所增加。


表3 两方案热负荷损失概率Tab.3 Probability of heating load loss in two schemes
由表3可知,鲁棒方案的Rh远小于基准方案,即相较于基准方案,鲁棒方案的热负荷损失风险大幅降低。这是由于鲁棒方案是在热电比偏差最严重的场景做出满足原有约束的决策,即确保对于任意不同的拟合误差,所得的鲁棒调度方案均可满足热负荷需求。
5 结 论
(1)考虑能量转换设备效率PLP函数的拟合误差后,采用鲁棒调度降低了负荷损失的风险。
(2)拟合误差不确定集的范围越大,RIES运行成本越高,系统抵抗误差不确定性的能力越强,系统运行鲁棒性也将更高。
(3)考虑能量转换设备效率PLP函数的拟合误差的鲁棒调度模型,不仅可用于计入单设备的影响,还可拓展计及多个能量转换设备效率PLP函数拟合误差的不确定性,进而考虑各不确定误差间的耦合和相关关系,使RIES优化调度方案更切合实际。
(4)在可计入部分负荷性能函数的其他优化或控制问题中,考虑函数拟合误差并应用于优化模型,可进一步提高系统鲁棒性和可靠性。

