几种典型函数的极值点偏移模型
2022-06-02 09:21广东省中山纪念中学528454邓启龙
中学数学研究(江西) 2022年6期
广东省中山纪念中学 (528454) 邓启龙
函数极值点偏移问题是近几年高考的热点,也是高考复习中的重点和难点.本文归纳总结了几种典型的函数极值点偏移模型,并举例说明这些模型在函数极值点偏移问题中的应用.
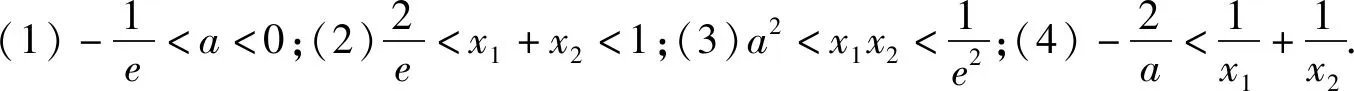
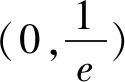
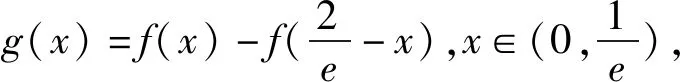
基本模型1在函数极值点偏移问题中有广泛的应用.
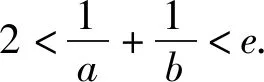
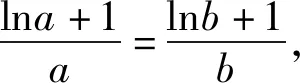
例1中的函数f(x)=x(1-lnx)可转化为基本模型1中的函数模型,由基本模型1中的结论可得以下命题模型.
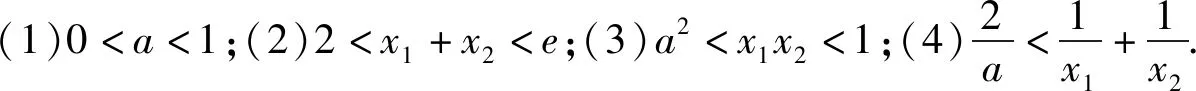
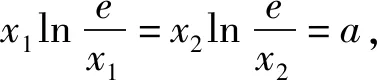
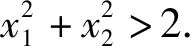
在水利工程中,堤坝渗水一直是影响工程质量的一个主要因素,并且也给堤坝的实际使用带来许多的不便,因此,堤坝的防渗施工非常重要。但是受多方条件的影响,堤坝的防渗水施工一直得不到有效提升,在这多方影响因素中,防渗水施工技术是主要的因素,因此,有必要在研究堤坝主要渗水情况的基础上,就堤坝的防渗加固技术做一番深入的分析,通过对堤坝防渗加固施工技术的分析,达到提高堤坝的防渗水性,提升堤坝工程质量的目的。
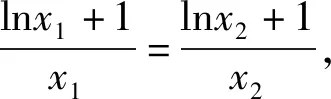
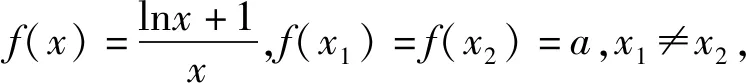
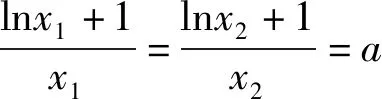
除了基本模型1,在函数极值点偏移问题中经常出现以下函数模型.
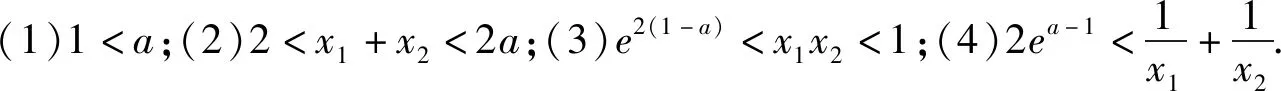
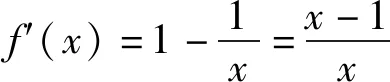

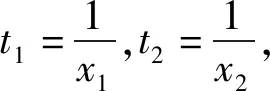
基本模型2在函数极值点偏移问题中也有广泛的应用.
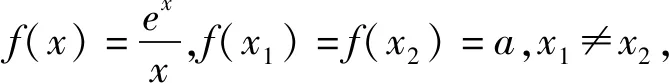
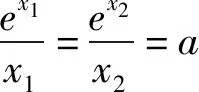
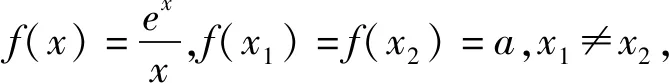
例4 已知函数f(x)=xlnx-ax+1有两个零点x1,x2,证明:1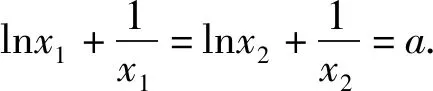

猜你喜欢
新世纪智能(数学备考)(2021年10期)2021-12-21
新世纪智能(数学备考)(2021年10期)2021-12-21
建材发展导向(2021年18期)2021-11-05
建材发展导向(2021年7期)2021-07-16
建材发展导向(2021年7期)2021-07-16
建材发展导向(2021年23期)2021-03-08
数学学习与研究(2020年16期)2020-12-28
语数外学习·高中版中旬(2020年10期)2020-09-10
建材发展导向(2019年11期)2019-08-24
建材发展导向(2019年11期)2019-08-24

