类比中的“真伪”

摘要：在初中数学的教学中，有很多概念、性质以及运算规律是通过类比的方法得到的，这是因为类比是初中学生比较容易接受的推理方法.类比求两个自然数最小公倍数的方法，学生提出解决三个自然数的最小公倍数的方案，发现了类比的结论不一定是正确的，因此类比最简公分母的概念，提出了求三个以上自然数的最小公倍数的解决方案.

关键词：类比;自然数;最小公倍数;最简公分母

中图分类号：G632文献标识码：A文章编号：1008-0333（2022）14-0056-03

收稿日期：2022-02-15

作者简介：曲敏（1983.6-），女，山东省潍坊人，研究生，中学二级教师，从事初中数学教学研究.

数学是离不开推理的.义务教育阶段要求注重学生思考的条理性，而不要注重推理的形式.从而可见，推理在数学中的重要地位.推理分为合情推理和演绎推理.从小学到中学，学生学习数学是通过观察、尝试、估算、归纳、类比、画图的活动发现规律，猜测某些结论，其中以归纳、类比在数学推理中的地位比较重要.法国著名数学家拉普拉斯（Laplace，1749-1827）说过：“甚至在数学里，发现真理的工具也是归纳和类比.”数学中的许多结论都是经过归纳和类比得到的.

1 类比中的“伪”

青岛版八年级上册数学课本第三章分式一章是类比分数提出分式的概念和性质，而3.4分式的通分一节中，学生类比分数的通分知道了分式的通分的关键是找出所有分式的公分母;分式的公分母是找出所有分式分母的最小公倍数，最小公倍数可以被任何一个分式的分母整除，学生类比分数的公分母，尝试找出兩个分式的公分母，并举出很多符合公分母的例子，因此学生知道了分式的公分母是无穷无尽的，让学生找到最简单的公分母，从而学生确定了求解分式最简公分母的方法.接下来有这么一道例题：将下面的分式通分y/2x，1/3xy，3x/4xy.经过分析，学生明确了例题中的分式特点：分式的分母都是单项式.根据分式分母确定最简公分母的步骤，需要先确定这几个分式分母的最小公倍数，结果大部分学生认为最简公分母的系数是24，教材解法中确定的最简公分母的系数是12.学生坚持自己的观点是正确的，学生以求2，3的最小公倍数为例.由于两个数除了1之外没有其他公因数，因此，2，3最小公倍数是2×3=6.类比求两个自然数的最小公倍数的方法，学生认为求2，3，4的最小公倍数与求2，3的最小公倍数是一致的.因为学生发现2，3，4这三个数的最大公因数除1之外没有其他公因数，因此，他们很肯定地认为2，3，4的最小公倍数就是2×3×4=24.

有些同学虽然不知道12为什么是2，3，4的最小公倍数，但是他们知道12是2，3，4的公倍数，因为12能被这三个数整除，并且12<24，那么24肯定不是这三个数的最小公倍数，因此说明了类比求两个自然数最小公倍数的方法求三个自然数的最小公倍数是不一定正确的.由此学生意识到类比得出的结论并不可靠.虽然学生因为自己的失败而感到懊恼，但是本人鼓励学生不要气馁，这一失败给学生提供了一次亲身经历，类比的结论不一定正确，一扫几日本人也为此找不到解决方法的愁云.

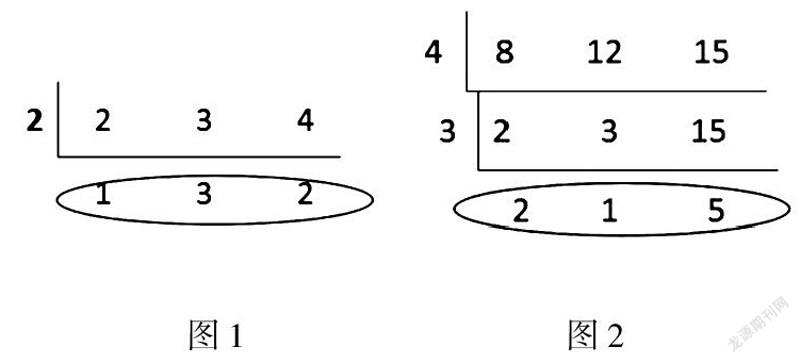
在课上，本人把自己总结的求三个自然数最小公倍数的方法向学生做了介绍：先求出任意两个数的最小公倍数，然后再求这个最小公倍数与第三个数的最小公倍数.即先求2，3的最小公倍数6，再求6，4的最小公倍数12.或者先求2，4的最小公倍数4，再求4，3的最小公倍数也是12.虽然学生学会了本人总结的方法，但是本人觉得这个方法并不是一个好的方法.于是，课后本人又在百度上搜索了一下相关的问题.有一个方法很不错，解法如图1：

短除号左边的2是2与4的公约数，短除号下面1，2分别是2，4除以公约数2得到的，3与公约数2无关，那么短除号下面的3是原封不动的，椭圆中的三个数两两互质，因此，2，3，4的最小公倍数是2×1×3×2=12.下面再用这个方法求8，12，15的最小公倍数如图2.

第一个短除号左边的数4是8，12的公因数，第一个短除号下面的2，3，15是4整除8，12，15的商，但是4不能整除15，那么15原封不动.第二个短除号左边的数3是3，15的公因数，第二个短除号下面的数是3整除2，3，15的商，3不能整除2，那么2是原封不动的.最后椭圆中的三个数两两互质，所以8，12，15的最小公倍数是4×3×2×1×5=120.探究其实质不难发现，当三个自然数的公因数是1时，如果它们的最小公倍数是这三个数的乘积，这个乘积中含有一些多余的因数，如8，12相乘后，乘积中含有42，而与4×3×2×1×5=120相比，显然多出了因数4，那么根据这一方法分析还得知12与15相乘后，乘积中就多出了因数3，所以，这三个数的乘积“掺杂”了多余的因数，显然“大”了.

课后反思时，本人再一次梳理了本节的知识脉络，分式的通分关键是确定公分母，取各分母系数的最小公倍数与所有字母因式的最高次幂的积作为最简公分母.类比单项式，本人发现每一个数都可以看成是几个因数的乘积，根据最简公分母取字母因式的最高次幂，求2，3，4的最小公倍数可以采用以下的方法进行：2=1×2，3=1×3，4=2， 2，3，4的最小公倍数应该是1×2×3=12，以上因数1可以省略，这种情况仅限于质数.如2，3看作一个字母的单项式，系数与次数皆可省略，因此它们直接看作为指数为1的幂即可.再如求8，12，18的最小公倍数，8=2，12=2×3，18=2×3，立刻能找出它们的最小公倍数为2×3=72.以上可以看出，求两个以上自然数的最小公倍数可以把每个数转化为几个因数相乘的形式，它们的最小公倍数是相同因数的最高次幂的积.对于有些数中不存在的因数，我们可以看作是n（n为除1之外的任意自然数）.短除法的缺点是求多个自然数的最小公倍数时，过程繁琐，书写麻烦，多个自然数放在一起容易漏掉某两个数的公因数，把自然数看作几个因数乘积的方法是比较直观简练的，适用于求多个自然数的最小公倍数.把自然数转化为几个因数的乘积时，可以按照因数的大小排列，无需按照次数的大小排列，这样有利于查找几个自然数中含有相同的公因数和不同的公因数，防止遗漏.

2 类比中的“真”

以上是类比中的“伪”，尽管“伪”中的结论是错误的，但是它对新的解题思路形成是非常有帮助的.下面我从类比中的“真”的角度，来说明类比得出的结论可以是正确的.

对于刚刚升入初中的学生来说，他们的数学基础是在小学中形成的，学生学习有理数是困难的.例如，在学习相反数的时候，学生知道4与-4是一对相反数，学生无法判断a和-a是一对相反数.因为初一学生的思维特点是从具体到抽象，当他的思维中存在大量的实例时，才能上升到抽象思维的层面上，尽管这种抽象思维还不成熟.在刚刚结束的期中考试中，有一道题要求把几个有理数标在数轴上，错误率最高的是 -（-3），学生大都标在数轴-3的位置上.课下找了几个做错的同学座谈，学生不知道这个数表示的是-3的相反数，也不知道它可以转化为（-1）×（-3）.在课余时间，我又把这两种方法讲给做错的学生，收效甚微，甚至是今天讲完明天就忘了.当我因为这个问题一筹莫展的时候，一个学生的提示让我眼前突然一亮.那是学习了《整式的加减》这一章中的《去括号》一节后，一个学生跑过来说：“今天讲的这个去括号，我觉得可以用在 -（-3）上，这个括号外面是负号，去掉括号后，-3变成了+3”.学生为了验证她说的是正确的，还给我举了一个多重符号的例子.学生寫下“-{-[+（-2020）]} ”并分析这个多重符号的题应从去小括号开始，去掉小括号后是 -{-[-2020]}，去掉中括号后是 -{+2020}，去掉大括号后是-2020，听完学生的分析后，我给了她大大的一个赞，肯定了她的解题思路是正确的，我也从中发现了初一学生可以应用类比推理获得解题思路.

有理数的运算也可以通过类比的方式找出与小学学过的计算的相同之处和不同之处，对于判断有理数的运算是否正确，是非常有帮助的.例如，小学学过的运算律——加法运算律和乘法运算律对有理数来说依然成立，乘法对加法的分配律亦是如此;小学学过的减法是加法的逆运算，除法是乘法的逆运算，有理数同样遵循;小学里学习了除法知道除数不能为零，分数的分母不能为零，有理数也没有改变这样的规定;小学学习了除以一个数等于乘以这个数的倒数，有理数的除法运算也是按照此规则进行的……如果说课前导入在数学中起到至关重要的作用，那么经过类比挑选的实例就是课前导入的重头戏.因此，一节课的成败在于是否选择好具有典型的实例，并且尽量覆盖面大一些，学生在实例中总结归纳，可以得到近似正确的结论，尽管结论不是最完美的.

猜想的思维基础的第一位就是逻辑思维，而类比推理也是逻辑思维中的一份子.猜想作为创新思维的一个重要环节，尽管会出现意想不到的错误，甚至得出的结论会被否定，但是不能否定它是一个摆脱传统思维模式束缚的有利途径，同时告诉学生科学研究就是这样的，总是在失败中徘徊，甚至是从头再来.这对于培养学生严谨科学地科研态度是至关重要的.

参考文献：

[1] 义务教育数学课程标准（2011版）[M].北京：北京师范大学出版社，2012.

[2] 十三院校协编组.中学数学教材教法总论[M].北京：高等教育出版社，1980.

[3] 展涛.义务教育教科书数学（八年级上册）[M].青岛：青岛出版社，2013.

[4] 赵振威.中学数学教材教法第1分册·总论[M].上海：华东师范大学出版社，2000.

[5] 林康义，唐永强.比较·分类·类比[M].沈阳：辽宁人民出版社，1987.

[责任编辑：李璟]