河流微孔曝气系统充氧性能优化试验

张文龙，杨雪梅，王浩岚，李 轶

(河海大学环境学院，江苏 南京 210098)

曝气技术作为一种污染河流治理的重要技术，不仅可以提高水体溶解氧浓度，利于好氧微生物降解有机污染物，还会增强水体的扰动作用，提高河流的自净能力，从而促进污染河流生态系统的恢复[1-3]。其中，微孔曝气因其具有充氧能力强、氧利用率高等优点[4]，被广泛应用于污染河流水质及生态修复。然而，在实际工程应用中，微孔曝气器的选型与布设多依赖于工程经验，未考虑河流水质等因素对氧传质过程的影响，导致微孔曝气系统的复氧效率普遍低于30%，并且产生较高的能耗[5-6]。因此，研究如何提高河流微孔曝气系统的氧传质效率，优化曝气系统的充氧性能，对降低曝气系统能耗具有重要意义。

探究微孔曝气系统氧传质过程的影响因素，并对其进行优化，可以提高曝气系统的充氧性能，从而减少曝气量，节约能耗[7]。河流微孔曝气系统的氧传质过程受多种因素的影响，对于微孔曝气器而言，其曝气量[8-10]、曝气器孔径[11-12]及曝气水深[13-14]均可产生直接影响；同时，水质因素如温度、pH值[15-17]、总溶解性固体[18-19]、离子强度、悬浮固体[20]、COD浓度[21]、表面活性剂浓度[22-24]等，也会改变水体的理化性质及气泡的流体力学行为，从而影响微孔曝气的氧传质效率[25]。目前已有研究主要集中于污水处理厂曝气池中氧传质过程单因素的影响，针对河流微孔曝气系统影响因素的研究较少。与污水处理厂曝气池相比，河流系统水深较浅，水质情况复杂多样，其氧传质过程的主要影响因素与曝气池存在差异。此外，不同因素之间存在的交互作用也会对氧传质过程产生较大影响，导致仅采用单因素试验难以达到最佳的优化效果。因此，研究河流微孔曝气系统氧传质过程的影响因素及其交互作用，对优化曝气系统的充氧性能至关重要。

本文通过单因素试验探究5种因素对河流微孔曝气系统氧传质过程的影响规律，并在此基础上，采用中心复合试验设计进行响应面优化分析，构建河流微孔曝气系统的氧体积传质系数优化模型，优化曝气器的选型及布设，提高微孔曝气系统的充氧性能，节约能耗，以期为微孔曝气系统充氧性能的优化提供参考。

1 材料与方法

1.1 试验装置

试验装置如图1所示，其主体为一个0.6 m×0.6 m×1.0 m的有机玻璃立方体槽，顶端开口。水槽内安装一个微孔曝气器，并与气体转子流量计、压力表及空气压缩机相连。在水槽中部水深处安装一个溶解氧数字电极，连接电脑，每30 s记录一次溶解氧的质量浓度。考虑实际河流水深情况及试验装置的限制，试验水深设置为0.8 m。

图1 试验装置示意图(单位：m)

1.2 设备与仪器

钛合金微孔曝气器直径为100 mm，试验中选用的孔径分别为5 μm、10 μm、20 μm、40 μm和100 μm；气体转子流量计的量程为1～10 L/min，精度为±2%；压力表精度为±2%；全无油静音空气压缩机的功率为680 W，容积为10 L； 数字型溶解氧电极(CLEAN, CS4751D)精度为±0.2%。

1.3 试验材料

所需的试剂包括亚硫酸钠、六水合氯化钴、氯化钠、无水葡萄糖、十二烷基苯磺酸钠(SDBS)，均为分析纯；试验用水为自来水。

1.4 试验方法

通过标准氧体积传质系数来表征微孔曝气系统充氧性能，可用来衡量水体的增氧效率，计算公式为

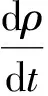
(1)

K=KLaθ(20-T)

(2)

式中：ρ为曝气过程水体中溶解氧质量浓度的测量值，mg/L；t为曝气时间，h；KLa为氧体积传质系数，表示单位时间内向单位体积水中传递氧的量，h-1；K为标准氧体积传质系数，h-1；ρT为试验水温为T时饱和溶解氧质量浓度，mg/L；ρ0为曝气前的初始溶解氧质量浓度，mg/L；θ为温度修正系数，一般取1.024；T为试验水温，℃。

通过文献调研和预试验结果分析，确定了5个对标准氧体积传质系数存在显著影响的因素，分别为曝气器孔径(d)、曝气水深(h)、河流水质因素中的盐度(S)、BOD5质量浓度(ρBOD5)、典型阴离子表面活性剂SDBS质量浓度(ρSDBS)。综合考虑微孔曝气器技术参数、试验水量、试验周期等因素，将本试验中的曝气流量确定为5 L/min。每组试验周期约为3 h，水温变化范围为0.2 ℃，最终根据试验结果对标准氧体积传质系数进行分析，因此，试验中可忽略水温变化对试验结果的影响。

选择试验所需的曝气器孔径并将其安装在相应的水深处，向水槽中分别添加氯化钠、无水葡萄糖以及SDBS，将试验用水配制成所需浓度，然后按照CJ/T 475—2015《微孔曝气清水氧传质性能测定》进行充氧试验。

a.单因素试验。单因素试验是在其他因素一定的情况下，分别观测曝气器孔径(5 μm、10 μm、20 μm、40 μm、100 μm)、曝气水深(20 cm、30 cm、40 cm、50 cm、60 cm)、盐度(0 g/L、1 g/L、2 g/L、3 g/L、4 g/L)、BOD5质量浓度(0 mg/L、3 mg/L、6 mg/L、9 mg/L、12 mg/L)、SDBS质量浓度(0 mg/L、1 mg/L、2 mg/L、3 mg/L、4 mg/L)对标准氧体积传质系数的影响规律，各因素的取值范围基于微孔曝气器技术参数以及城市河流的实际情况而定。

b.响应面优化试验。根据中心复合设计(central composite design，CCD)方法，设计5因素5水平的响应面试验方案(表1)。试验以K为响应值，孔径、曝气水深、盐度、BOD5质量浓度及SDBS质量浓度5个影响因素均在5个不同水平下进行研究。

表1 响应面试验设计因素及水平

c.模型验证。采集5条河流水样，分别测定其盐度、BOD5及SDBS质量浓度，通过优化模型分析得到最佳微孔曝气器孔径及曝气水深，并在该最佳参数下进行曝气试验，计算得到标准氧体积传质系数。

2 结果与讨论

2.1 单因素对微孔曝气系统充氧性能的影响

单因素对标准氧体积传质系数的影响如表2所示。在曝气水深为60 cm、盐度为0 g/L、BOD5质量浓度为0 mg/L、SDBS质量浓度为0 mg/L的条件下，考察曝气器孔径对K的影响。由表2可知，随着微孔曝气器孔径的增大，K逐渐减小。微孔曝气器孔径会直接影响其产生的气泡尺寸，在相同曝气量下，孔径越大，则产生的气泡尺寸越大。气泡越大，一方面会增加水体的扰动强度，加速氧在水体中的扩散作用，促进氧传质，另一方面可减小液膜的厚度，降低氧的传质阻力，同样有利于氧传质过程；同时，气泡越大，比表面积越小，气液传质界面面积减小，会抑制气液氧传质过程。随着孔径的增大，气液传质界面面积的减小对氧传质过程的影响更加显著，成为主要的影响因素[11]，因此K随孔径的增大而减小，本试验结果与上述研究所得结论一致。

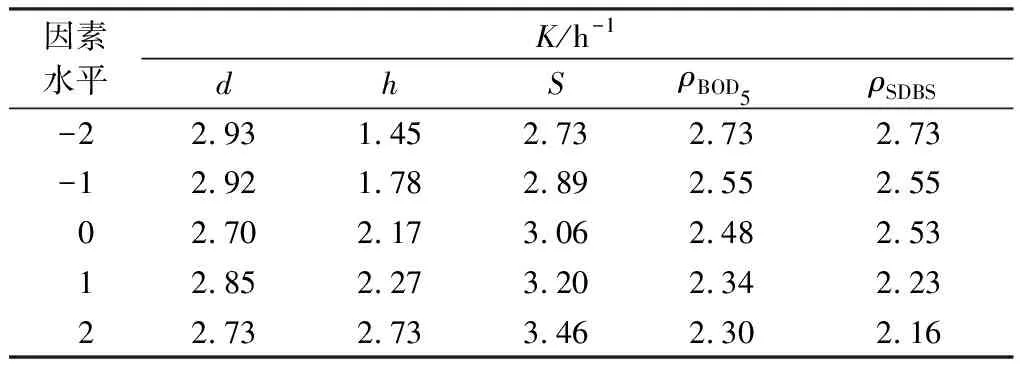
表2 不同因素对氧体积传质系数的影响

在微孔曝气器孔径为100 μm、盐度为0 g/L、BOD5质量浓度为0 mg/L、SDBS质量浓度为0 mg/L的条件下，考察曝气水深对K的影响。由表2可知当水深由20 cm增加至60 cm，K由1.45 h-1增大至2.73 h-1，增幅显著。尹训飞等[13]探究了水深对微孔曝气充氧性能的影响，结果表明，曝气水深为1～6 m时，K随着水深的增大先减小后趋于不变，与本试验研究所得结论并不一致。其原因可能是本试验采用了曝气水深为20～60 cm的浅水曝气系统，水深增大使得气泡在水中的停留时间以及气液接触时间增加，而浅水系统在曝气条件下具有强烈的气液湍动作用，液膜阻力较低，使得气液表面更新速率加快，在两方面的共同作用下提高了氧传质速率。

在微孔曝气器孔径为100 μm、曝气水深为60 cm、BOD5质量浓度为0 mg/L、SDBS质量浓度为0 mg/L的条件下，考察盐度对K的影响。由表2可知，水体盐度增大时，K有明显的上升趋势，盐度由0 g/L增大至4 g/L时，K由2.73 h-1上升为3.46 h-1。有学者研究发现，随着盐度的增大，液体的表面张力会线性增大[18]，使得产生的气泡尺寸变小，从而降低气泡聚并的概率及上升的速率，促进了气液传质作用，本研究的试验结果与该结论一致。

在微孔曝气器孔径为100 μm、曝气水深为60 cm、盐度为0 g/L、SDBS质量浓度为0 mg/L的条件下，考察BOD5质量浓度对K的影响。由表2可知，K随水体BOD5质量浓度的增加而逐渐减小。该结果与孙剑辉等[21]的研究结论一致，其原因可能是本研究通过添加无水葡萄糖来调节水体中BOD5质量浓度，随着葡萄糖浓度的增加，液体的黏度增大[26-27]，导致氧的扩散速率减小，黏度增大还会促进气泡的聚并作用，进而使得产生的气泡变大，上升速率加快，K值降低。

在微孔曝气器孔径为100 μm、曝气水深为60 cm、盐度为0 g/L、BOD5质量浓度为0 mg/L的条件下，考察SDBS质量浓度对K的影响。由表2可知，当SDBS质量浓度由0 mg/L升高至4 mg/L时，K随之减小。程香菊等[22]基于气泡理论探究了表面活性剂对微孔曝气系统增氧性能的影响，结果表明，SDBS质量浓度为1 mg/L时可促进氧传质，SDBS质量浓度为1～5 mg/L时，随着浓度的增加，K降低。本研究中，K在SDBS质量浓度为1 mg/L时并没有出现拐点，而是随SDBS质量浓度的增大而减小。产生这种趋势的主要原因是表面活性剂同时含有亲水基团和疏水基团，亲水基团易于进入水相，而疏水基团远离水相，导致其在气液界面聚集，并在气液界面形成一层液膜，使得表面张力降低，阻碍氧气传输，从而抑制了氧传质过程。

2.2 响应面法优化充氧性能试验

2.2.1优化模型及方差分析

采用Design-Expert 12软件设计生成响应面优化试验方案，试验共50组(8组为重复实验)，按照该方案进行试验，结果见表3, 孔径、曝气水深、盐度、BOD5及SDBS质量浓度5个影响因素的水平值分别记为x1、x2、x3、x4、x5。通过软件对试验结果进行多元回归拟合分析，得到关于标准氧体积传质系数与因素水平值的二次多项式回归方程(式(3))。

K= 2.23-0.041 8x1+ 0.308 7x2+ 0.084 7x3-

0.006 8x4- 0.092 3x5- 0.025 3x1x2+

0.000 9x1x3+0.009 1x1x4+ 0.040 9x1x5+

0.025 9x2x3- 0.024 7x2x4+ 0.023 4x2x5+

0.004 1x3x4-0.037 8x3x5-0.012 2x4x5+

(3)

回归模型的方差分析及显著性检验结果如表4所示。设置显著水平α= 0.05，则当P< 0.05时为显著，反之即为不显著。由表4可知，所得模型的F值为23.87，P< 0.000 1，远小于0.05，表明该回归模型非常显著。模型的决定系数R2为0.942 7，变异系数Cv= 4.32%(<10%)，表明该模型可以解释94.27%响应值的变化，拟合度较高。根据方差分析的F值可知，各因素影响的显著性由大到小顺序为：曝气水深、SDBS质量浓度、盐度、曝气器孔径、BOD5质量浓度。

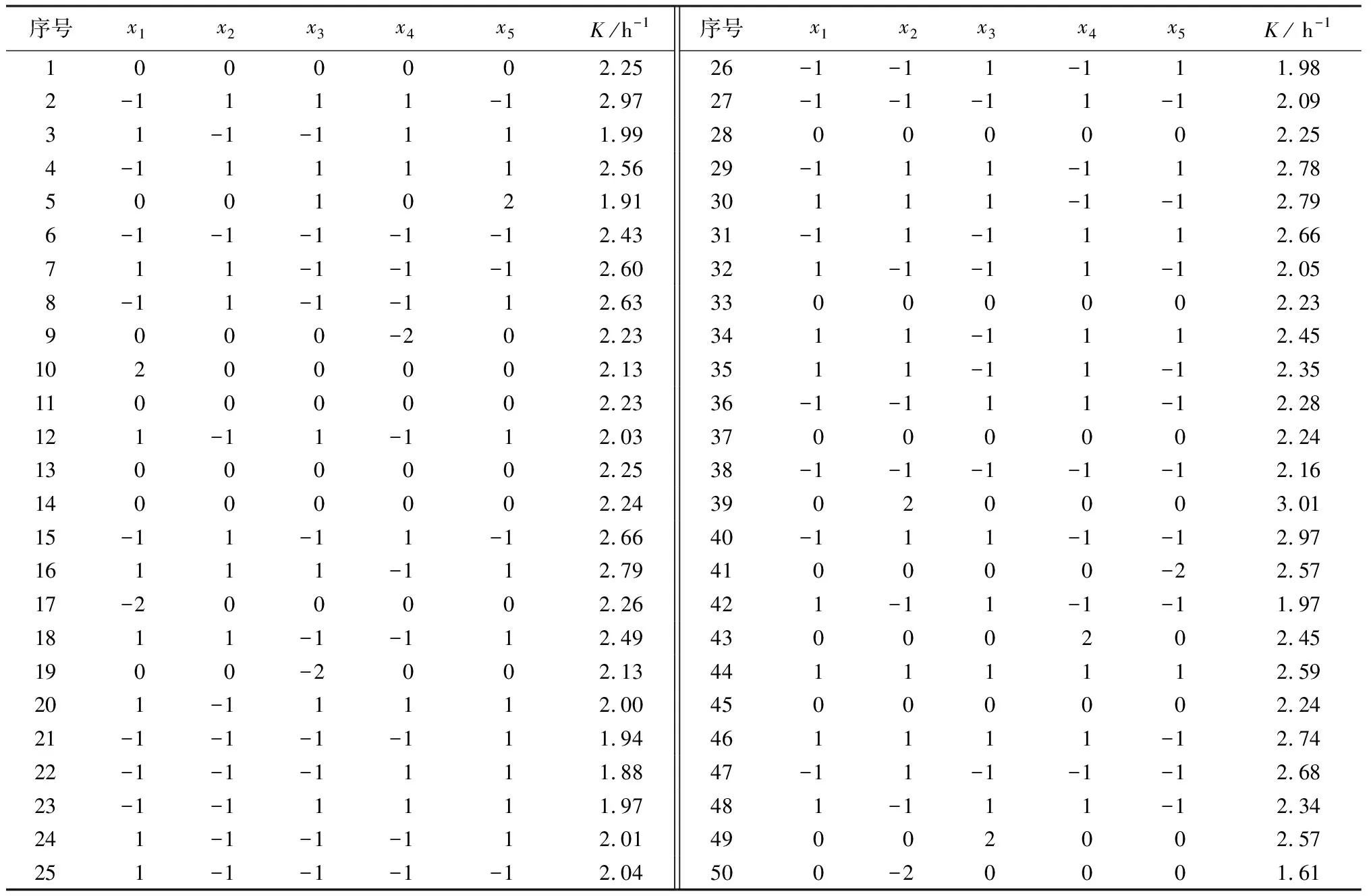
表3 试验设计方案及结果

表4 回归模型的方差分析和显著性检验

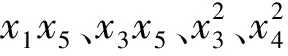
K= 2.23 - 0.041 8x1+ 0.308 7x2+ 0.084 7x3-

0.092 3x5+0.040 9x1x5- 0.037 8x3x5+

(4)

当已知水体的盐度、BOD5及SDBS质量浓度时，即式(4)中x3、x4、x5为定值，通过求解二元函数的最大值，可得到微孔曝气系统的最佳孔径及安装水深。将该最佳孔径和水深设置为曝气参数，从而实现微孔曝气系统充氧性能的优化。

2.2.2响应面分析

采用Design-Expert 12软件绘制响应曲面图，可直观反映本试验所考虑的各因素对响应值的交互作用。将其他因素固定为中间值，即可获得任意2个因素交互作用的结果，共得到10组响应曲面，如图2所示。响应曲面坡度越陡则表明响应值对该影响因素的变化越敏感；响应曲面的轮廓呈凸起、凹陷或马鞍状则表明所对应的两个影响因素之间的交互作用显著。

由图2可知，在试验设置范围内，K随曝气水深的增大而增大，且响应曲面坡度较大，表明水深对K的影响非常显著，盐度、SDBS质量浓度及孔径也存在显著影响，而BOD5质量浓度的影响不显著；孔径和SDBS质量浓度、盐度和SDBS质量浓度对K存在显著的交互作用，这与模型显著性分析所得结论一致。由于K受曝气水深变化的影响程度最大，因此对曝气水深进行优化可以显著提高K。盐度、SDBS质量浓度及孔径对K影响的显著程度小于曝气水深，原因可能是其相互之间存在的交互作用产生了抑制的效果。BOD5质量浓度对K的影响不显著，其原因可能是本研究采用自来水作为试验水体进行模拟，未考虑实际河流水体中微生物的作用。孔径和SDBS质量浓度存在交互作用的原因可能是SDBS亲水亲油的性质，使其易于在微气泡的界面积累，增加了界面的氧传质阻力并降低了氧传质速率。盐度和SDBS质量浓度的交互作用主要是由于无机盐会增加SDBS在气液界面的积累，从而减小表面张力，抑制气液氧传质过程。由于孔径和SDBS质量浓度、盐度和SDBS质量浓度对K存在显著的交互作用，因此，对微孔曝气系统充氧性能进行优化时不能仅考虑其中一种因素的作用，还需考虑另一种因素不同水平的影响。

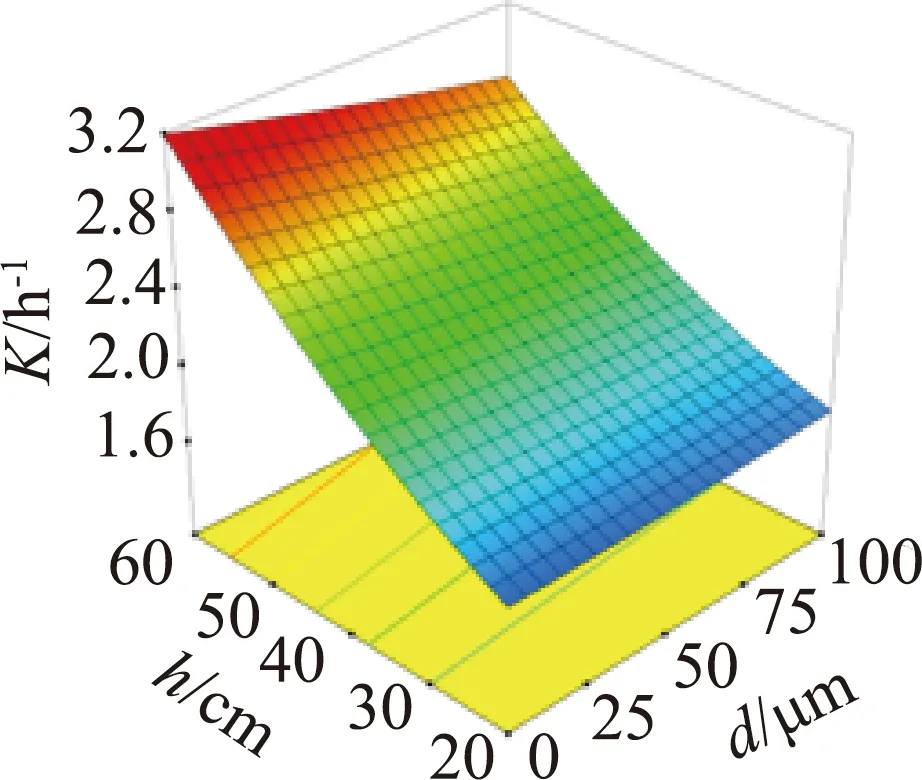
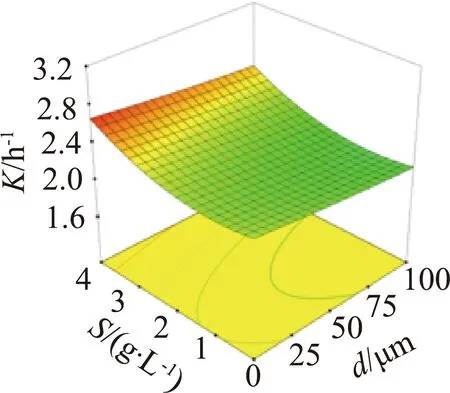
(a)孔径和曝气水深 (b)孔径和盐度

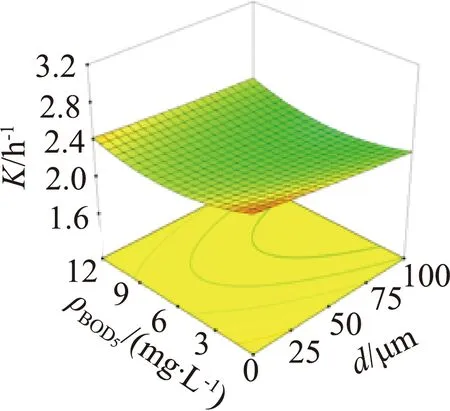
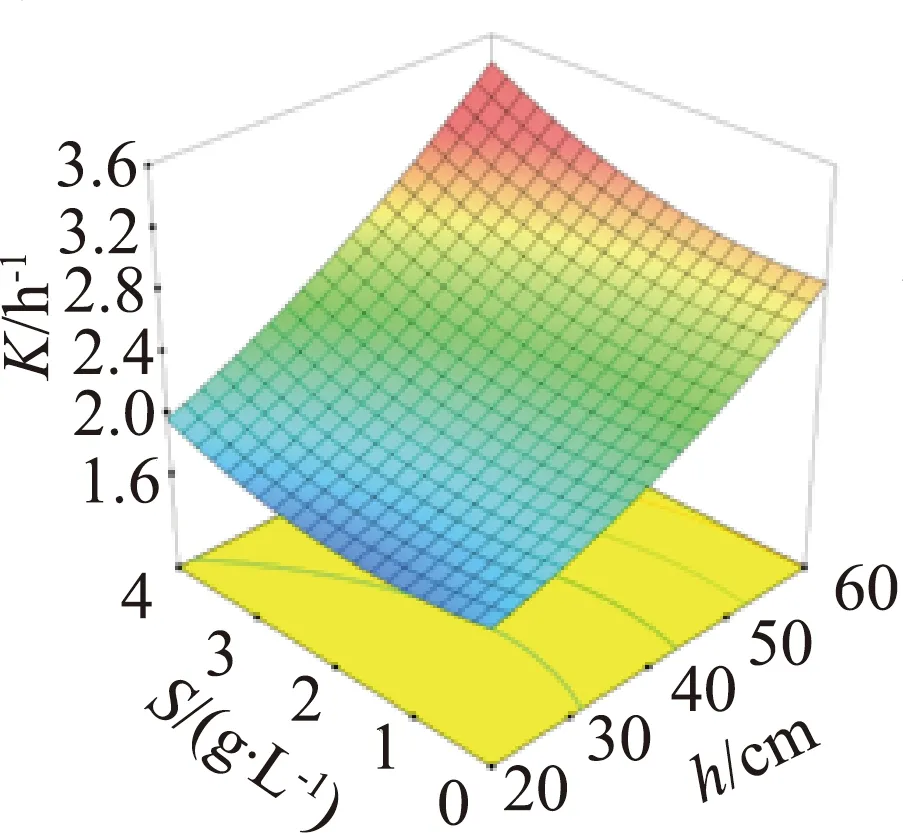
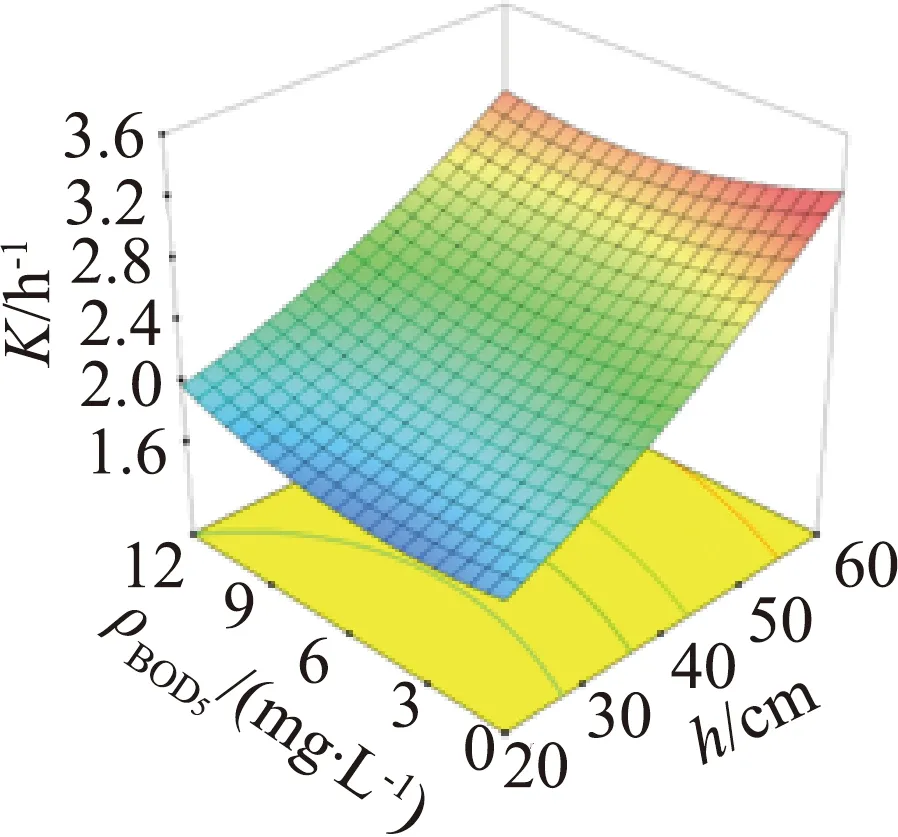
(c)孔径和BOD5质量浓度 (d)孔径和SDBS质量浓度 (e)曝气水深和盐度 (f)曝气水深和BOD5质量浓度

(g)曝气水深和SDBS质量浓度 (h)盐度和BOD5质量浓度 (i)盐度和SDBS质量浓度 (j)BOD5质量浓度和SDBS质量浓度

2.2.3模型验证

采用优化模型对实际河流微孔曝气系统的曝气参数进行优化，得到5组水样在本试验研究范围内的最佳曝气参数。通过模型预测，得到的K分别为3.12 h-1、2.96 h-1、3.02 h-1、3.08 h-1和2.88 h-1。为验证模型预测结果的准确性，在最佳参数下对采集的水样进行曝气试验，计算出K分别为3.06 h-1、2.91 h-1、3.05 h-1、3.01 h-1和2.92 h-1，模型预测结果与试验测试结果的相对误差平均值仅为1.67%(< 5%)，表明预测值与试验值基本吻合，进一步说明通过该模型优化曝气参数具有一定可靠性和准确性。

3 结 论

a.单因素试验结果表明，微孔曝气器孔径、曝气水深、盐度、BOD5质量浓度、SDBS质量浓度均可影响标准氧体积传质系数。

b.响应面分析结果表明，5种因素对标准氧体积传质系数影响的显著程度由大到小分别为：曝气水深、SDBS质量浓度、盐度、微孔曝气器孔径、BOD5质量浓度；微孔曝气器孔径和SDBS质量浓度、盐度和SDBS质量浓度对标准氧体积传质系数存在显著的交互作用，在对微孔曝气系统充氧性能进行优化时不能仅考虑单一因素的影响。

c.以标准氧体积传质系数最大为优化目标，通过回归模型分析实际河流水体微孔曝气治理的最佳参数，并进行试验验证，得到模型预测值与试验值的相对误差平均值仅为1.67%，表明该模型准确可靠。可通过该模型对曝气器的选型与布设进行优化，从而提高微孔曝气系统的充氧性能。