水库抗暴雨能力概率预报的降雨情景构建方法
吴志勇,汪瑛琪,何 海,李 源,孙昭敏
(河海大学水文水资源学院,江苏 南京 210098)
我国现有中小型水库9万多座。中小型水库集水面积小,洪水汇集快,预报预见期短[1-5],安全运行风险突出。水库抗暴雨能力预报是实现中小型水库安全运行的有效方法。该方法根据水库集水区下垫面和水库调度的动态情况,通过预演不同降水总量下水库的水位变化过程,实现对预报水库剩余防洪库容所能容纳的降水量的预报[6-10]。为防汛部门精准实施水库调度方案,及时发布水库预警,支撑水库预报、预警、预演和预案工作,对保障我国中小型水库防洪安全具有重要意义[10-12]。
当前水库抗暴雨能力的计算主要通过设定不同等级降水总量,结合水文模型与水库调度方案,得到不同降水总量与水库最高水位的关系曲线;在此基础上,依据水库设计水位,反推水库可容纳降水总量,即该水库当前状态的抗暴雨能力[11-14]。该方法已在广东、福建、江西和辽宁等地区广泛应用。然而,传统抗暴雨能力预报方法中降雨输入的时程分配大多基于一场典型暴雨[14],通过同倍比缩放得到不同降水总量下的降雨输入,未能考虑到降水总量、降雨历时和降雨时程分配之间的相关性及对产汇流的影响,使得水库抗暴雨能力计算结果具有较大的不确定性。为此,本文在水库抗暴雨能力计算中,引入Copula函数,构建考虑降水总量、降雨历时和降雨时程分配相关性的降雨情景,生成同一降水总量下不同降雨历时及时程分配概率的降雨情景,将其应用到水库抗暴雨能力计算中,以实现水库抗暴雨能力的概率预报,提高水库抗暴雨能力的可应用性。
1 研究区概况与方法
1.1 研究区概况
选取位于江苏省新沂市东部淋头河上游的阿湖水库以上流域作为研究区域(图1)。该水库是一座以防洪为主的中型水库,总库容4 032万 m3,汛限水位25.50 m,设计水位27.73 m。水库集水面积193 km2,位于南北气候过渡带和海陆交接带,多年平均降水量为875.0 mm,年最大降水量为1 318.0 mm,汛期降水占年降水量60%左右。选取阿湖水库水文站点2010—2020年汛期(5—9月)的逐时降水量资料开展研究。

图1 阿湖水库以上流域及水系分布
1.2 研究方法
水库抗暴雨能力是指在当前水库集水区下垫面状态和水库调度方式下,在一段时间内水库剩余防洪库容所能容纳的降水量。设定不同等级的降水总量,输入水文模型进行产汇流计算和水库调洪演算,建立不同等级降雨与水库最高水位的关系,通过设计水位反推水库当前抗暴雨能力。
传统水库抗暴雨能力计算方法中,各级降水总量下仅考虑一种确定的降雨时程分配方案,例如典型暴雨同倍比缩放或均匀分配,忽略了降水总量、降雨历时和降雨时程分配的相关性,以及在同一降水总量等级下不同历时降雨情景的不确定性。
由于在降水总量一定的情况下,不同历时及雨型对产汇流有较大影响,进而影响水库抗暴雨能力的计算结果。因此,本文提出考虑不同降水总量下不同降雨历时概率的降雨情景构建方法,并基于暴雨洪水同频率假设,实现水库抗暴雨能力的概率预报,提高水库抗暴雨能力的可用性。该方法主要包括3个步骤:①从汛期连续的时段降雨资料中,划分出独立降雨事件,提取每场降雨事件的降雨特性(降水总量、降雨历时和降雨时程分配);②基于Copula函数构建降水总量和降雨历时的联合概率分布;③确定降水总量与降雨历时分级下的代表雨型。
1.2.1降雨场次挑选
本文通过设定降雨阈值(最小降水总量)与降雨间歇时间[15](两场降雨事件之间的无雨时间间隔),从连续的时段降雨资料中划分出独立降雨事件开展研究。
1.2.2降水总量与降雨历时的联合分布
Copula函数是一种描述变量间相关性的连接函数,已被众多学者用来描述降水总量与降雨历时的相依结构[16-20]。参照Sadegh等[21]的相关研究,本文选用26种Copula函数作为备选函数,求解降水总量和降雨历时的联合分布,以得到同一降水总量下不同降雨历时的概率。主要步骤如下:
a.选择常用的伽马(Gamma)分布、广义极值(generalized extreme value,GEA)分布、广义帕累托(generalized Pareto,GPA)分布、对数逻辑(Loglogistic)分布、对数正态(Lognormal)分布和威布尔(Weibull)分布作为降水总量与降雨历时的备选边缘分布。采用极大似然估计(maximum likelihood estimate,MLE)方法估计边缘分布的参数,依据贝叶斯信息准则(Bayesian information criterion,BIC)和赤池信息准则(Akaike information criterion,AIC)的最小统计量选择降水总量R与降雨历时T的最优边缘分布FR(R)和FT(T),采用Kolmogorov-Smirnov(K-S)检验方法进行拟合优度检验。
b.将优选的边缘分布带入Copula备选函数中,分别采用MLE和基于拉丁超立方体抽样的马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法[22]估计Copula参数,基于极大似然值(maximum likelihood values,MLV)最大、AIC和BIC最小准则比较两种参数估计方法,并确定最优Copula函数F(R,T)=C(FR(R),FT(T)),F(R,T)表示降水总量R和降雨历时T的联合分布函数。通过均方根误差RMSE、纳什效率系数NSE,并结合Q-Q图(quantile-quantile plot)检验最优的Copula函数。RMSE、NSE和Q-Q图表示构建Copula联结的双变量概率与经验联合概率的拟合程度,当拟合效果好时,RMSE为0,NSE为1,Q-Q图中散点落在45°对角线附近。

1.2.3降水总量和降雨历时分级下代表雨型的确定
一场降雨事件中,降雨强度是随时间变化的,即存在降雨时程分配。不同降雨事件具有不同的降雨时程分配,且受降水总量和降雨历时的影响。由于降雨历时可以反映降雨的集中程度,从某种程度上亦能代表降雨的时程分配。当降水总量一定时,若降雨历时短,则降雨集中且强度大;若降雨历时长,则降雨分散且均匀。因此,基于已划分的降雨场次,对降雨时程分配进行分类,并结合降水总量和历时的分级,采用每种分级下频率最高的雨型作为代表雨型。结合第1.2.2节中生成的降水总量与降雨历时,即可生成完整的降雨情景。
为了消除降雨事件中其他降雨特性对时程分配分类的影响,使降雨随时间的变化是唯一影响不同时程分配的因素,首先要对降雨时程分配进行无量纲化处理[23]:
τ=t/T
(1)
dτ=Dt/R
(2)
式中:τ为时刻t的无量纲时间,τ∈(0,1];T为一场降雨事件的降雨历时;dτ为无量纲累计降水总量,即降水总量随时间的累计百分比,dτ∈(0,1];Dt为时刻t的累计降水总量。
其次,将每场降雨事件的无量纲降水总量累计曲线均分成K个时段(K值为研究区平均降雨历时)。此时,无量纲时间τm=m/K(m=1,2,…,K)对应的无量纲累计降水总量值为dm。将每场降雨的K个dm值作为其K个属性输入到聚类方法中,以雨型划分。采用基于欧几里得距离进行分类的K均值聚类算法计算不同时程分配的K个属性值间的欧几里得距离,并通过迭代算法最终得到不同类别的时程分配。同一类别内的雨型数据相似度较高,而不同类别间的数据相似度较低。最后,采用列联法统计分析在降水总量和历时分级下各雨型的频率,频率最高的雨型为该分级下的代表雨型。将代表雨型与第1.2.2节中的降水总量、降雨历时及其概率相结合,即可得到在同一降水总量下不同概率的降雨情景。
2 实例验证
2.1 降雨场次提取
利用阿湖水库报汛站汛期降雨数据提取降雨事件的准则为:①场次降水总量大于或等于20.0 mm,若该降水总量选取得过大,会导致降雨场次的样本量较少,若阈值较小,可能会出现一种天气状况下的降雨被分为两场降雨;②无雨持续时间大于或等于6 h[24],若无雨持续时间小于6 h,则认为是一场降雨事件,反之则为两场降雨事件。
根据该原则,阿湖水库以上流域共挑选出83场降雨,流域平均每年约发生7.5场降水总量大于20.0 mm的降雨事件,每场降雨事件的平均降水总量达到44.9 mm,场次降水总量最高达144.4 mm,平均降雨历时为16.6 h,最大降雨历时为48 h,其中最大降雨历时与最大降水总量相对应。降水总量和降雨历时通过了95%的相关性显著检验,表明该地区适合采用Copula函数建立降水总量与降雨历时之间的联合分布。
2.2 降水总量与降雨历时的联合分布
采用二维Copula函数构建降水总量与降雨历时的联合分布。不同边缘分布下降水总量与降雨历时的BIC和AIC指标值如表1所示,依据BIC和AIC最小原则优选出的边缘分布分别为GPA分布和Weibull分布,且两种边缘分布函数均通过了K-S拟合优度检验。降水总量边缘分布中的形状、尺度和位置参数分别为k=0.43,σ=23.87,θ=20.0;降雨历时边缘分布中的尺度和形状参数分别为A=18.45,B=1.55。经验分布与理论分布的拟合结果如图2(a)和(b)所示,可见经验频率与理论频率非常接近,拟合效果较好。因此,对阿湖水库地区降水总量和降雨历时的模拟适宜采用GPA分布和Weibull分布。

表1 降水总量与降雨历时不同边缘分布下的BIC和AIC指标值



(a) 降水总量边缘分布 (b) 降雨历时边缘分布 (c) 联合概率Q-Q图
分别采用MLE和MCMC[22]方法估计Copula函数的参数,表2为依据MLV最大、AIC和BIC最小准则优选出的Copula备选函数。MCMC算法下的参数估计优化了原本在MLE中表现不好的函数(Roch-Alegre、t和Gaussian),使该函数更适用于表示变量间的联合分布。虽然MLE法可以高效地估计参数,但对于有些Copula函数形式,MLE法容易陷入局部最优解,而MCMC算法下的参数寻优具有多个初始链,可以在全局寻优[22]和迭代次数足够多的前提下,更易找到最优解。
在本研究区中,两种参数估计算法下的最优联合分布函数形式均是BB1,并且在两种参数估计方法下的指标值类似。理论联合概率与经验联合概率的RMSE(0.171 5)和NSE(0.995)均表现较好,结合降水总量和降雨历时的联合分布Q-Q图(图2(c)),发现图中所有散点均落在45°对角线附近,由此可知,BB1形式可以较好地拟合降水总量和降雨历时的联合分布,最终其联合分布和条件分布为
C(u,v)={1+[(u-θ1-1)θ2+
(v-θ1-1)θ2]1/θ2}-1/θ1
(3)
CT|R(v|u)=[1+(x+y)1/θ2]-1/θ1-1·
(x+y)1/θ2-1x1-1/θ2u-θ1-1
(4)
式中:C(u,v)表示降水总量和降雨历时的联合分布函数;u和v分别表示降水总量与降雨历时的边缘分布函数,u=FR(R),v=FT(T);CT|R(v|u)表示在降水总量为R发生的概率u下,降雨历时为T发生的条件概率;x=(u-θ1-1)θ2;y=(v-θ1-1)θ2;参数θ1和θ2在MCMC算法优化下的值分别为0.220 3和1.33。
2.3 代表雨型分析
将83场降雨事件的降雨过程线进行无量纲化处理,根据流域平均降雨历时(约17 h),将降雨过程线分为17段,即K=17,并采用K均值聚类方法对其进行分类。我国雨型划分采用的聚类数一般为3~6[25],若聚类数太少,会忽略频率低但对防洪较不利的雨型;若聚类数太多,则会导致聚类雨型间差异较小。本实例选择聚类数为4和5,得到的雨型分类如图3所示。阿湖水库地区的雨型主要以单峰型为主,雨峰在前期且降雨主要集中在前中期的降雨事件频率最高。聚类数为4时,R4-1、R4-2、R4-3、R4-4雨型的发生频率依次为32.53%、28.92%、20.48%和18.07%。雨型差异主要体现在雨峰位置和降雨集中程度。R4-3的雨峰较R4-1更靠前,R4-1的降雨集中在雨峰两侧,而R4-3的降雨集中在前期,雨强在雨峰后陡然减小。R4-4的雨峰较R4-2更靠后,R4-2的降雨集中在雨峰之前,而R4-4的降雨集中在雨峰之后。相较于聚类数为4时的雨型划分结果,聚类数为5时,R5-1、R5-2、R5-3、R5-4、R5-5雨型的发生频率依次为33.73%、28.92%、20.78%、10.84%、6.02%。将雨峰在中(R5-2)、极端在前(R5-4)和极端在后(R5-5)细分出来。R5-2为双峰型,两个雨峰接近且降雨集中在中期,发生频率较高为28.92%。虽然R5-5发生频率仅有6.02%,但在实际防洪规划设计及管理中该雨型情况较不利,需要单独着重考虑这一雨型。因此,最终选择雨型聚类数为5。

表2 两种参数估计方法下的优选函数及指标值




(a)R4-1 (b)R4-2 (c)R4-3 (d)R4-4





(e)R5-1(f)R5-2(g)R5-3(h)R5-4(i)R5-5
本文将降水总量分为3级:20~50 mm、50~100 mm和100 mm以上,将降雨历时分为4级:1~6 h、6~12 h、12~24 h和24 h以上,采用列联法统计在降水总量和降雨历时分级下各雨型的频率(表3)。在降水总量和降雨历时分级下,各雨型频率和代表雨型均有较大的差别。对于20~50 mm的降雨事件,雨型多样,随着降雨历时的增加,雨型从以R5-3和R5-1为主变换为以R5-1和R5-2为主,选择最有可能的雨型(频率最高)为代表雨型。对于50~100 mm的降雨事件,12 h以内R5-3发生频率较高,为代表雨型;在12~24 h内R5-1和R5-2居多;当降雨历时大于24 h时,R5-1和R5-5居多,均选择R5-1为代表雨型。当降水总量大于100 mm时(样本量较少),降雨历时以长历时为主,当降雨历时在12~24 h和24 h以上时,分别选择R5-2和R5-3为代表雨型;当历时较短时,选择对防洪较为不利的R5-5为代表雨型。

表3 5种雨型在降水总量和历时分级下的频率及代表雨型
2.4 同一降水总量下不同历时的降雨情景
以降水总量为40 mm、70 mm和110 mm为例,实际降雨情景和采用典型场次同倍比放大得到的降雨情景分别见图4和图5。依据式(4),挑选并计算条件概率P(T≤t*|R=r*)分别为0.1、0.5和0.9时生成的降雨情景结果见图6。3种条件概率分别代表在同一降水总量下,降雨历时为短、中和长的降雨情景,也可反映降雨集中、均匀和分散时的降雨情景。在实际降雨情景中,降雨历时随着降水总量的增加而增加。本文生成的降雨情景,在同一条件概率下,亦能够模拟出该特性。而采用典型场次同倍比放大得到的降雨情景,在不同降水总量下的降雨历时均为21 h(典型降雨历时为21 h),在降水总量较小时(如40 mm和70 mm),坦化了降雨过程,既不能反映实际降雨情况,也没有考虑对防洪的不利影响。
利用本文提出的方法生成的降雨情景,总是可以找到与实际降雨情景较为相似的降雨特性或者生成对防洪较不利的降雨情景。当降水总量为40 mm和70 mm时,条件概率为0.1时的降雨情景(图6(a)和(d))能够反映实际降雨情景的集中程度。由于仅考虑了在降水总量和历时分级下最有可能发生的雨型,在雨峰强度和雨峰位置上难免与实际降雨情景有出入。当降水总量为110 mm时,实际降雨情景中降雨历时为31 h,降雨主要集中在第20~30 h内。在本文方法生成的降雨情景中,虽然对于历时相似的降雨情景(图6(i)),雨峰与实际雨峰有较大差异,但条件概率为0.1的降雨情景(图6(g))历时短,降雨集中,其雨峰强度与实际降雨情景的雨峰强度相近,且该降雨情景对防洪十分不利。
因此,本文方法生成的降雨情景考虑了降水总量、降雨历时和降雨时程分配的相关性,可以较好地反映多种实际降雨情景或生成对防洪不利的降雨情景,并可定量计算同一降水总量下不同降雨情景的概率。
2.5 抗暴雨能力预报结果对比
以2020年7月12日8时阿湖水库的状况为例,该时刻库水位为25.54 m。将传统典型降雨同倍比缩放得到的降雨情景和本文生成的降雨情景分别输入到水库抗暴雨能力模型[14]中,传统方法预报此时阿湖水库的抗暴雨能力为160 mm,而本文方法预报的水库抗暴雨能力分布在146~169 mm区间内(图7),相应概率在9.9%~93.1%之间,其中160 mm的概率为62.2%。
实测结果表明,7月12日8时至7月15日8时实际降水总量为64.4 mm,水库水位于7月12日21时涨至最高(26.68 m),低于设计水位(27.73 m)1.05 m,实际发生降雨小于抗暴雨能力,水库仍有剩余库容。根据实测降雨和入库径流计算此次降雨产流系数为0.58,若将7月12日8时剩余的防洪库容(1 677万 m3)折算成水库抗暴雨能力为149.8 mm,该值为接近实际水库抗暴雨能力的一种情况,落在本文的预报区间内,发生概率为11.6%。从以上分析来看,利用本文提出的降雨情景构建方法,可以实现阿湖水库抗暴雨能力的概率预报,结果合理。



(a)降水总量40 mm、降雨历时5 h (b)降水总量70 mm、降雨历时13 h (c)降水总量110 mm、降雨历时31 h


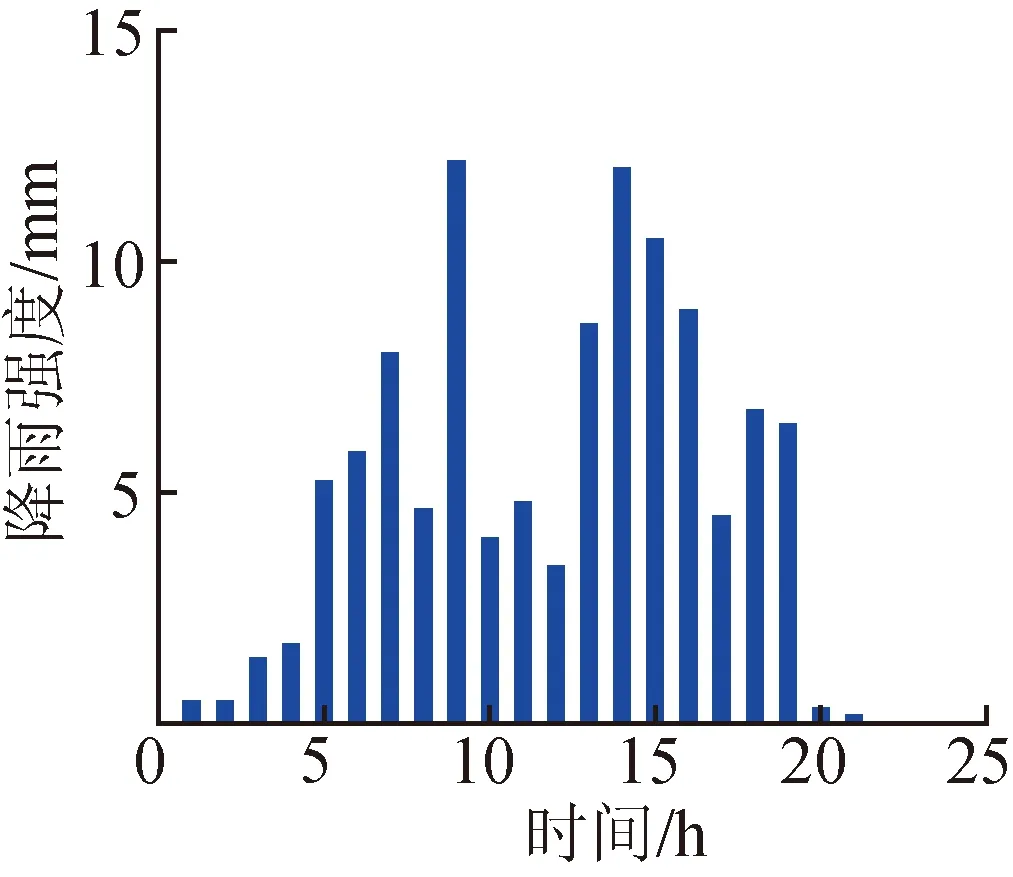
(a)降水总量40 mm (b)降水总量70 mm (c)降水总量110 mm



(a)P(t≤6 h|R=40 mm)=0.1 (b)P(t≤16 h|R=40 mm)=0.5 (c)P(t≤29 h|R=40 mm)=0.9



(d)P(t≤9 h|R=70 mm)=0.1 (e)P(t≤22 h|R=70 mm)=0.5 (f)P(t≤37 h|R=70 mm)=0.9



(g)P(t≤12 h|R=110 mm)=0.1 (h)P(t≤29 h|R=110 mm)=0.5 (i)P(t≤46 h|R=110 mm)=0.9

图7 阿湖水库2020年7月12日8时水库抗暴雨能力概率预报结果
3 结 论
a. 提出了基于Copula函数构建降水总量和降雨历时的联合分布,结合K均值聚类法得到的代表雨型,生成同一降水总量下不同概率降雨情景的方法。相比于传统典型暴雨放大方法的输入,本文将概率降雨情景应用到水库抗暴雨能力计算中,考虑了流域不同情况降雨的可能性及其对产汇流的影响,为实现中小水库抗暴雨能力从定量预报到概率预报,拓展中小水库抗暴雨能力预报方法提供了技术支撑。
b. 基于多样的Copula备选函数形式并结合MCMC参数估计方法,可较好地找到描述变量联合关系的最优Copula函数。在阿湖水库流域,BB1函数形式可较好地反映降水总量与降雨历时的联合分布。
c. 雨型聚类数选取需根据流域调整。通过对比不同聚类数结果下的降雨特性(如雨峰位置和降雨集中程度)和对实际防洪规划中不利雨型的考虑,分析选择合适的聚类数。在阿湖水库地区,雨型以单峰型为主,雨型聚类数为5较合适。

