基于人工侧线的履带装备水阻力计算方法

吴家雄 申焱华 杨舒迪 冯志鹏

北京科技大学机械工程学院，北京，100083

0 引言

近年来，城市内涝和河流水灾频发，造成了严重的人员伤亡和经济损失。城市内涝、河道清淤的作业环境复杂、危险因素多，需要依靠具备强涉水、高机动的履带式装备进行水下应急救援作业。在水流较为湍急的水域，水下履带装备的行走工作稳定性受到极大的影响，因此，研究水下履带装备的局部流场感知、水阻力估计的方法对水下履带装备的稳定性控制，以及应急装备的推广应用意义重大。水下应急抢险水环境浑浊，能见度低，水下空间环境复杂，导致视觉感知与声学感知应用受限，严重限制了水下履带装备的作业能力，所以，有必要研发一种应用于工程机械、不依赖光学和声学信号的水下履带装备与流场环境的交互方法。

受鱼类侧线感知[1]的启发，研究人员研制了一种基于压力传感器阵列的人工侧线系统，合理的传感器分布可以避免流场信息的丢失和冗余，从而更高效地识别流场信息。XU等[2-3]提出了基于均值和方差的特征重要性算法、距离评估的特征重要性算法以及信息冗余算法的最佳传感器放置位置确定方法，并验证了所提算法的有效性。

人工侧线系统可以通过传感器的压力分布规律实现对流场信息的主动感知[4]。目前，人工侧线系统已成功应用于机器鱼，实现了机器鱼在直线运动、转弯运动、滑翔运动和螺旋运动中的状态估计[5-6]以及近壁面流场识别[7]。同时，人工侧线系统更广泛地应用于水下航行器，实现了移动载体流场感知[8]以及水下机器人俯仰运动参数感知[9]。

相比机器鱼和水下航行器，履带装备的结构更为复杂，外形不具备流线型，现有的基于人工侧线的水下动载体的表面压力分布规律并不适用于水下履带装备。所以，有必要结合履带装备的表面压力分布特点，研究一种适用于水下履带装备的流场感知方法。

对于水下履带装备稳定性控制，主动感知局部流场的来流速度及来流方向是必要的，但是，仅通过有限的流场信息无法估算水下履带装备的整车水阻力。目前，海洋工程中，履带装备水阻力可以根据Morison理论[10]进行计算，其中的水阻力系数为基于简单结构计算的经验值[11]，没有建立履带装备外形与水阻力系数的精确关系。在水下履带装备行走过程中，不同的来流角度导致履带装备迎流面的尺寸与外形存在较大的差异，而水阻力系数无法跟随来流角度的变化进行动态更新，这导致水阻力的计算产生较大的误差。

为了解决以上问题，本文提出了一种基于人工侧线的履带装备水阻力计算方法，利用人工侧线系统采集履带装备模型表面的压力信号，根据不同来流角度和来流速度的数据分布规律，对局部流场的来流角度和来流速度进行预测，结合水阻力系数的辨识结果，估算履带装备的水阻力，为水下履带装备行走、工作的实时稳定性控制提供基础。

1 人工侧线的履带装备实验分析

1.1 人工侧线感知机理

鱼类侧线系统包含表面神经丘和侧线管神经丘，分别用于感知局部流体的速度和加速度信号，经过神经中枢处理，对即时的位向和环境水动态信息做出判断，通过调整自身姿态以达到适应复杂水下环境的目的，如图1所示。

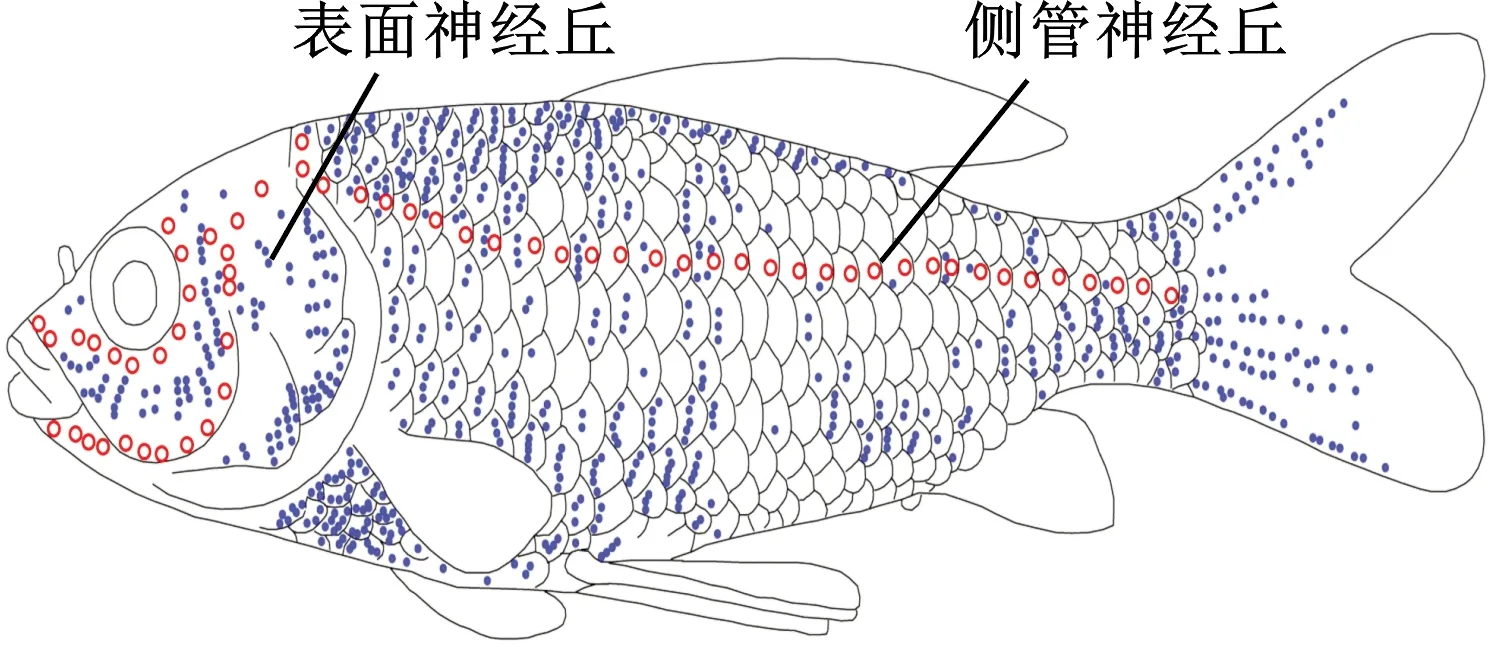
图1 鱼侧线系统Fig.1 Lateral line system

人工侧线是一种基于力学传感器阵列的仿生鱼侧线系统，通过采集流场的压力变化信息实现对来流速度和位置信息的感知。考虑不可压缩、等温的牛顿流体(密度ρ，黏度μ)，Navier-Stokes(N-S)方程可以表示为

(1)

由式(1)可知，压力-∇p和动量∇2V存在特定关系，水流流速的减小会伴随压力的增大，因此，通过水下装备的表面压力值的变化规律可以对来流方向、来流速度进行估计。当流体为同一介质时，流场中结构体表面对应点的压力仅与介质流速相关，与模型的尺寸无关。

本文应用人工鱼侧线系统对履带装备局部流场的来流角度和来流速度进行估计，并根据人工鱼侧线结果结合水阻力系数辨识结果计算履带装备的水阻力，流程如图2所示。

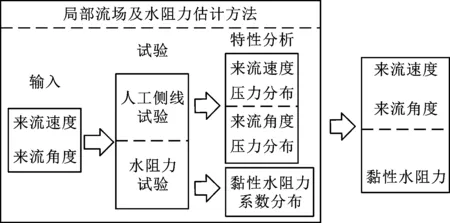
图2 水阻力计算流程图Fig.2 Flow chart of water resistance calculation

1.2 人工侧线的履带装备模型试验

参考鱼侧线系统的侧管神经丘分布规律，以及人工侧线系统在水下航行器的传感器布置方式[8]，在履带装备模型的同一高度对称等距选取12个数据采集点，并安装压力传感器，如图3所示。应用履带装备模型的人工侧线系统，主动感知局部流场的来流速度vw和来流角度θ，来流角度为履带装备的速度方向v与水流方向vw的角度。

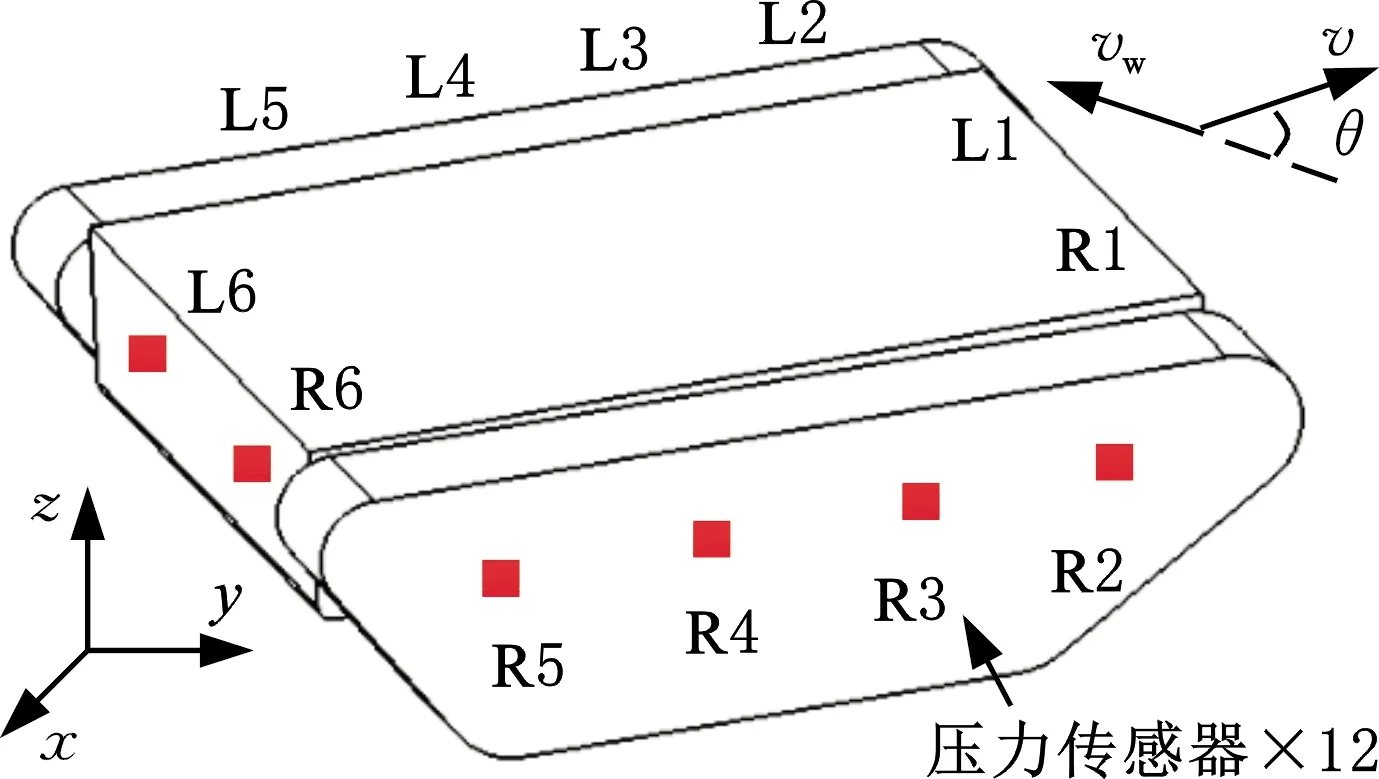
图3 履带装备压力传感器分布Fig.3 Track equipment pressure sensor distribution

根据履带装备模型的尺寸设计试验水槽，水槽的尺寸为2300 mm×600 mm×300 mm，水深200 mm，履带车模型的边缘到试验水槽内壁的距离为履带车模型宽度的2.5倍，避免了水阻力实验中的近壁效应，如图4a所示。应用型材构建水槽的支撑结构，并在水槽上搭建丝杠和导轨，通过连接的伺服电机控制滑台的移动速度，丝杠的长度为1700 mm，最大移动速度为0.6 m/s。履带车微缩模型与丝杠通过刚性连接杆连接，该连接方式对水下测试模型的流场分布造成的影响较小，不会影响人工侧线数据的采集精度[3，8]，如图4b所示。人工侧线使用的压力传感器的型号为MS5803-01BA，有效量程为1～130 kPa，分辨力为1.2 Pa，通过IIC协议编译12路数据采集卡，并制作数据显示界面，如图4b所示。

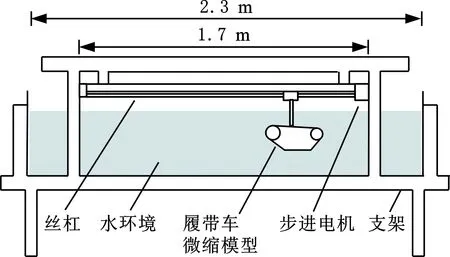
(a)试验平台示意图

(b)人工侧线采集系统图4 履带装备模型人工侧线试验Fig.4 Artificial lateral line test of track equipment model

1.3 人工侧线数据分布

在履带装备模型的人工侧线试验中，试验变量为履带装备模型的前进速度v和来流角度θ，履带装备模型的速度设置为0.3 m/s、0.4m/s和0.5 m/s，调整履带车模型的安装角度，将来流角度设置为0°、15°、30°、45°、60°、75°和90°，可以得到不同实验条件设置下的压力数据。

图5所示为来流角度0°、来流速度0.5 m/s时R1、R3、R6传感器的压力信号，传感器分别位于履带装备模型的前方、侧方和后方，平均压力值分别为196 Pa、-159 Pa和-98 Pa，由此可见，位于不同位置的传感器压力值差别较大。R1处于迎流面，压力值为正值；而R3、R6处于负压区，压力值为负。

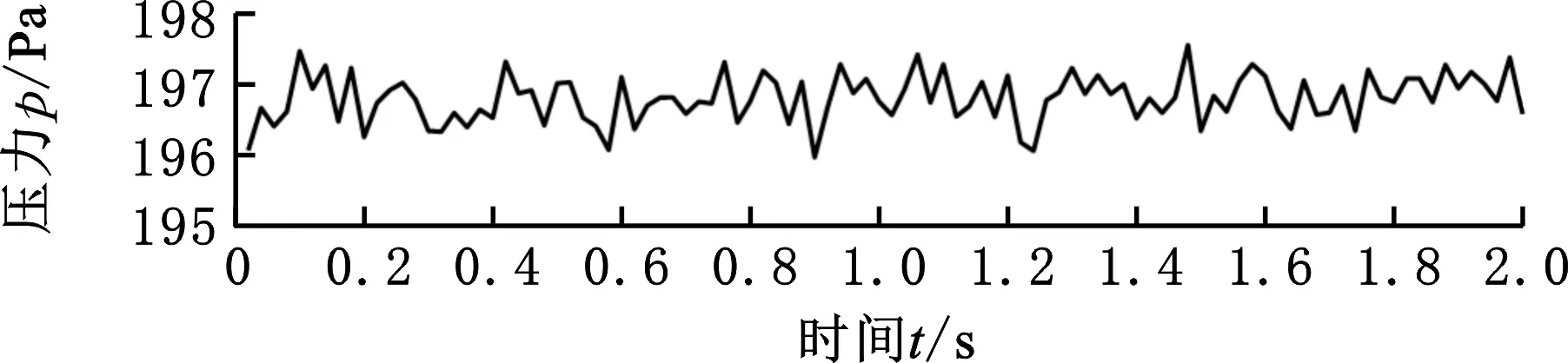
(a)R1

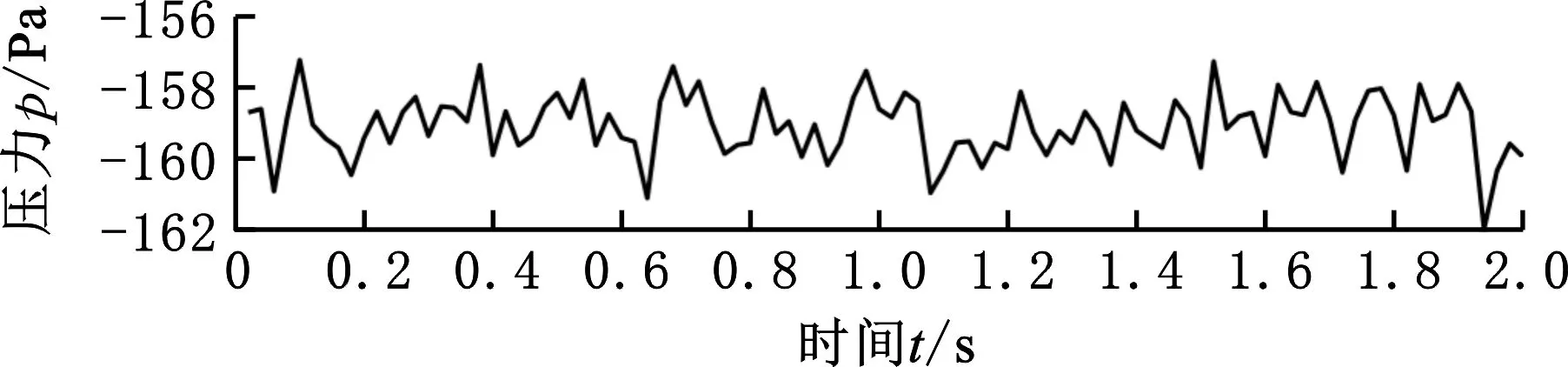
(b)R3

(c)R6图5 人工侧线信号Fig.5 Data of artificial lateral line

图6所示为来流角度0°时不同流速的压力分布，当水流速度发生改变时，履带装备模型的表面压力分布具有一定的规律性，履带装备模型前方的传感器L1和R1位置的压力最大，且与水流速度正相关。履带装备模型侧方的L2、L3、L4、L5和R1、R2、R3、R4位置的压力值变化较平缓，且随着水流速度的增大而减小。履带装备模型后方的L6和R6位置的压力值增大。

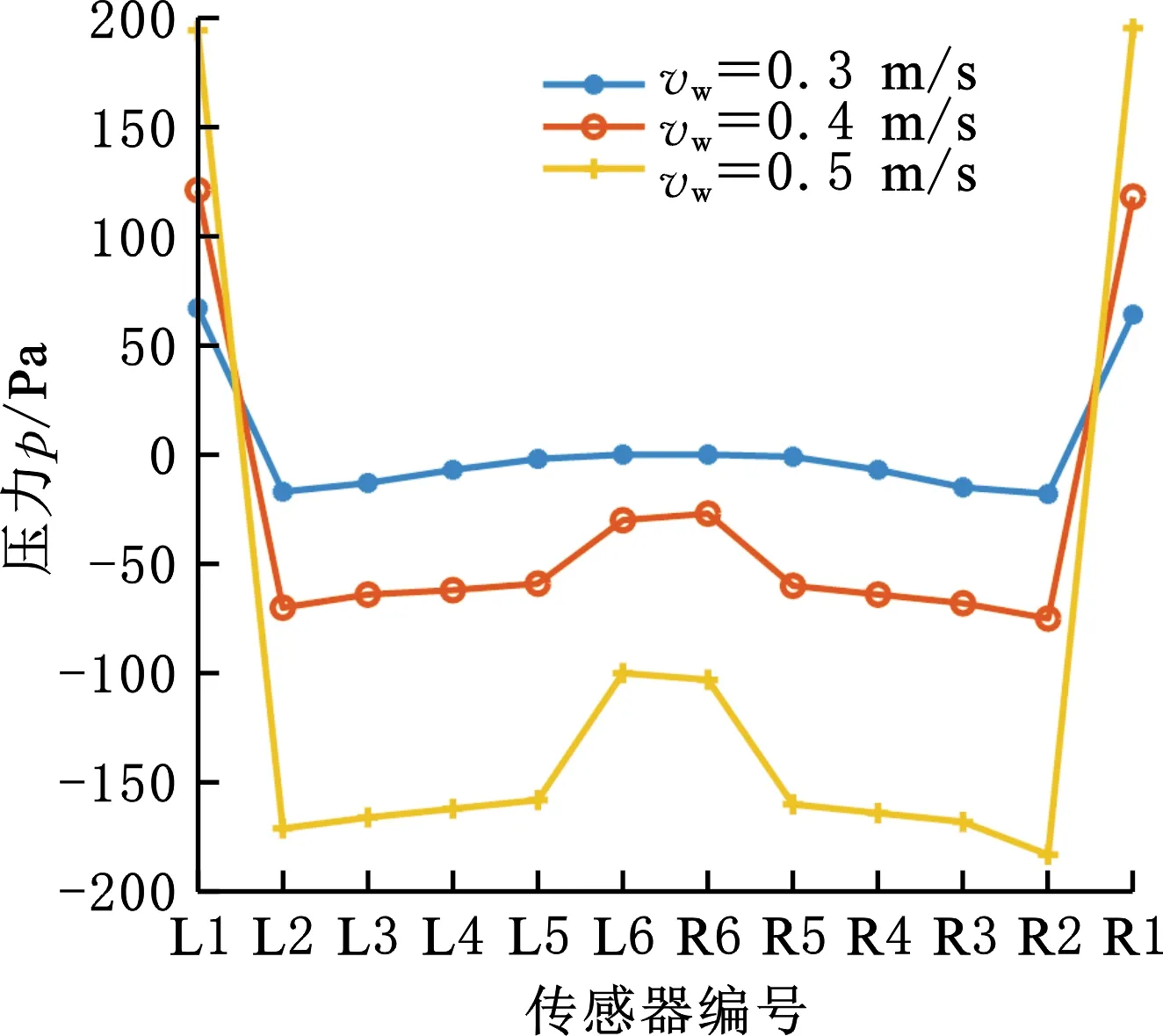
图6 不同流速的压力曲线Fig.6 Pressure curve of different inlet velocity

图7所示为来流速度0.5 m/s时不同来流角度的压力分布，当来流角度改变时，履带装备模型的表面压力分布呈现不同的规律。其中，迎流面与背流面的对称分布的传感器测量值差别较大，通过对称面的传感器测量值作差，可以凸显不同来流速度和来流角度的数据分布差别。

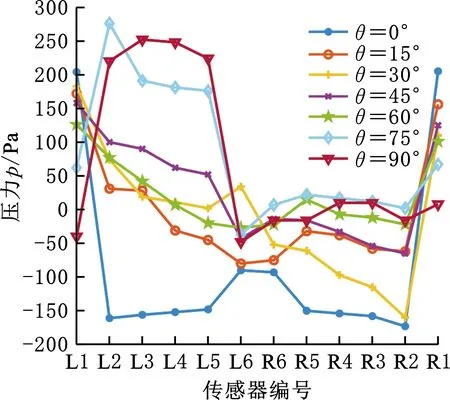
图7 不同来流角度的压力曲线Fig.7 Pressure curve of different inlet angle

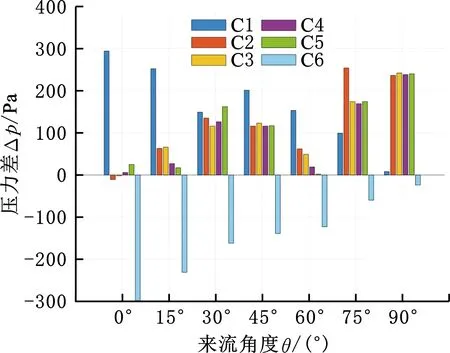
图8 不同来流角度的压力分布Fig.8 Pressure distribution of different inlet angle

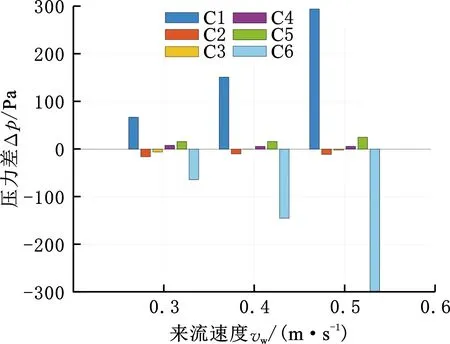
图9 不同来流速度的压力分布Fig.9 Pressure distribution of different inlet velocity

将12个压力传感器对称分为6组，C1组为L1和L6，C2组为L2和R2，C3组为L3和R3，C4组为L4和R4，C5组为L5和R5，C6组为R1和R6，将每组的压力值作差，可以得到图8和图9。图8所示为来流速度0.5 m/s时不同来流角度的6组传感器的压力分布，图9所示为来流角度0°时不同来流速度的6组传感器的压力分布。其中，压力最大值随着来流角度的改变而向来流面移动，每组传感器的压力值呈现非对称变化，差别较大。这是由于履带装备模型的外形较为复杂，对局部流场的改变较大，压力分布对来流角度的敏感性是人工侧线感知履带装备姿态的基础。

综上所述，应用人工侧线系统估计水下履带装备的来流速度和来流角度的方法如下：①将人工侧线系统的压力数据进行分组处理，与不同来流角度的压力分布数据进行相关性检测，判断当前时刻的来流角度；②根据来流角度与侧线系统的压力数据分布，与不同来流速度的压力分布数据进行相关性检测，判断当前时刻的来流速度。

以上来流速度和来流角度的估算方法需要以数据处理时的分类精度作为基础，本文的来流角度的检测精度为15°，来流速度检测精度为0.1 m/s。

2 履带装备的水阻力试验

2.1 波浪载荷计算理论

Morison理论最早应用于计算海洋中固定结构上的波浪力，同样可以近似计算水下行走装备的波浪载荷，例如深海集矿机的水阻力计算[12]。假设水下结构的存在不影响波浪的特性，则波浪载荷可以描述为波浪流体惯性力和黏性力的叠加。由于水下装备的行走速度较慢，可以忽略波浪载荷的惯性力项，则履带装备水下行走黏性水阻力可以表示为

Fw=0.5CwρwAm|vw-v|(vw-v)

(2)

式中，Cw为黏性水阻力系数；ρw为水密度；Am为履带装备辆迎水面积。

根据人工侧线得到履带装备模型的流场流速信息，可以对履带装备模型不同来流角度的水阻力进行计算，而计算的关键在于黏性水阻力系数与履带装备外形的关系，即黏性水阻力系数Cw的辨识。

2.2 水阻力学试验

为了获得黏性水阻力系数与履带装备外形的关系，将履带装备模型的人工侧线试验平台进行改装，用于测试水下履带装车模型的水阻力。在履带装备模型的后方安装力学传感器，测试履带装备模型不同来流角度与其前进速度的关系，如图10所示。压力传感器的型号为Kistler 9301B，有效量程为25 kN，分辨力为0.02 N，通过LMS与计算机连接采集数据。

图10 履带车模型的水阻力试验Fig.10 Hydrodynamic test of tracked vehicle model

2.3 数据处理及扩充

在履带装备模型的水阻力试验中，试验变量为履带装备模型的前进速度v和来流角度θ，履带装备模型的速度设置为0.3 m/s、0.4 m/s和0.5 m/s，来流角度设置为0°、45°和90°，履带装备模型的加速度设置为1 m/s2，可以得到不同试验条件设置下的压力数据，如图11所示。

(a)来流角度0°

(b)来流角度45°

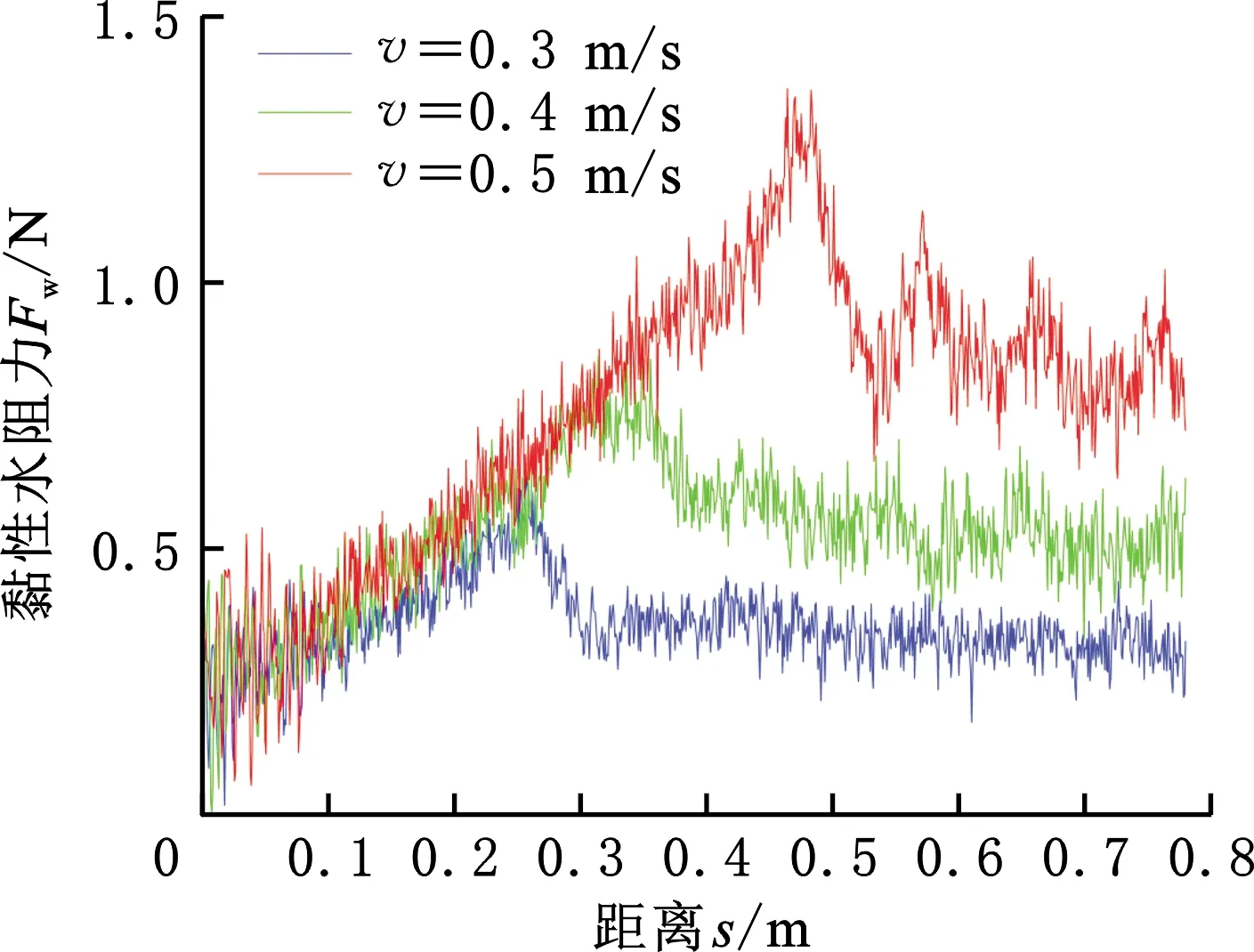
(c)来流角度90°图11 不同来流角度的履带装备模型水阻力测试Fig.11 Hydrodynamic test of tracked equipment model with different incoming flow angles

由图11可知，当水流速发生改变时，不同来流姿态的履带装备模型的水阻力变化具有相似的规律，其水阻力分布先增大后趋于稳定，这是由于履带装备模型的进行过程包括加速和均速两个阶段。根据实际工程需要，只需对履带装备模型的黏性水阻力进行计算分析，即匀速阶段。通过设置的步进电机目标速度和加速度，履带装备模型在0.1 s后达到均速状态，即0.3 m、0.4 m和0.5 m开始匀速前进，与图11中的数据变化趋势相符合。图11a中的黏性水阻力值最小，这是由于来流角度为0°时，履带装备模型的迎水面积最小。

履带装备应用场景为内河，以淮河水域为例，淮河的中下游水域平均流速为2.5 m/s，而试验中应用的丝杠最大前进速度为0.6 m/s。为了扩充样本数量，本文对履带装备模型的水阻力进行CFD仿真，模型选用标准k-ε湍流模型，模拟中的边界条件与水阻力实验保持一致，在后处理中提取履带装备模型的水阻力。模拟过程中的变量为履带装备模型的前进速度v和来流角度θ，与人工测试保持一致，履带装备模型的速度设置为0.3 m/s、0.4 m/s和0.5 m/s，来流角度设置为0°、15°、30°、45°、60°、75°和90°。图12所示为来流角度0°、来流速度0.5 m/s时的CFD仿真结果。

图12 履带车模型CFD表面压力Fig.12 CFD simulation of tracked vehicle model

提取与水阻力试验相对应的表面压力进行分析，如图13所示，模拟结果和试验结果的变化趋势保持一致且相对误差小于15%。对于水下履带式工程装备的水阻力估算，该相对误差在可接受的误差范围内。

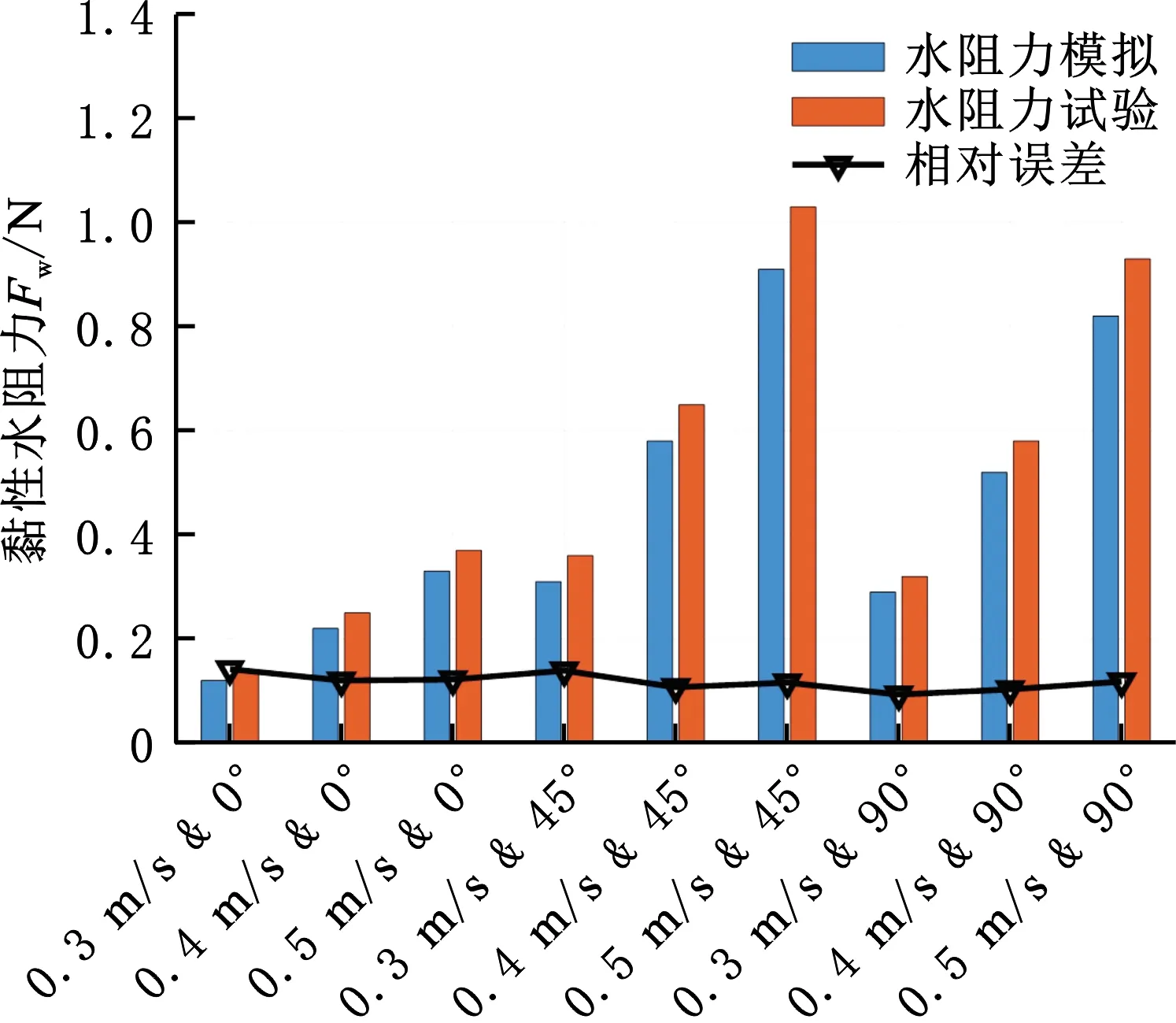
图13 水阻力试验和模拟结果对比Fig.13 Comparison of hydrodynamic experiment and simulation results

整合不同来流角度和来流速度的水阻力仿真数据并进行拟合，可以得到各来流姿态的黏性水阻力系数，如图14所示。根据水阻力的分布规律可知，当来流角度为45°时，履带装备模型的来流面积最大，但水阻力值小于来流角度为60°和75°时的履带装备模型。由此说明，履带装备模型的水阻力值与来流面横截面积成正相关，同时与来流面的外形有关。

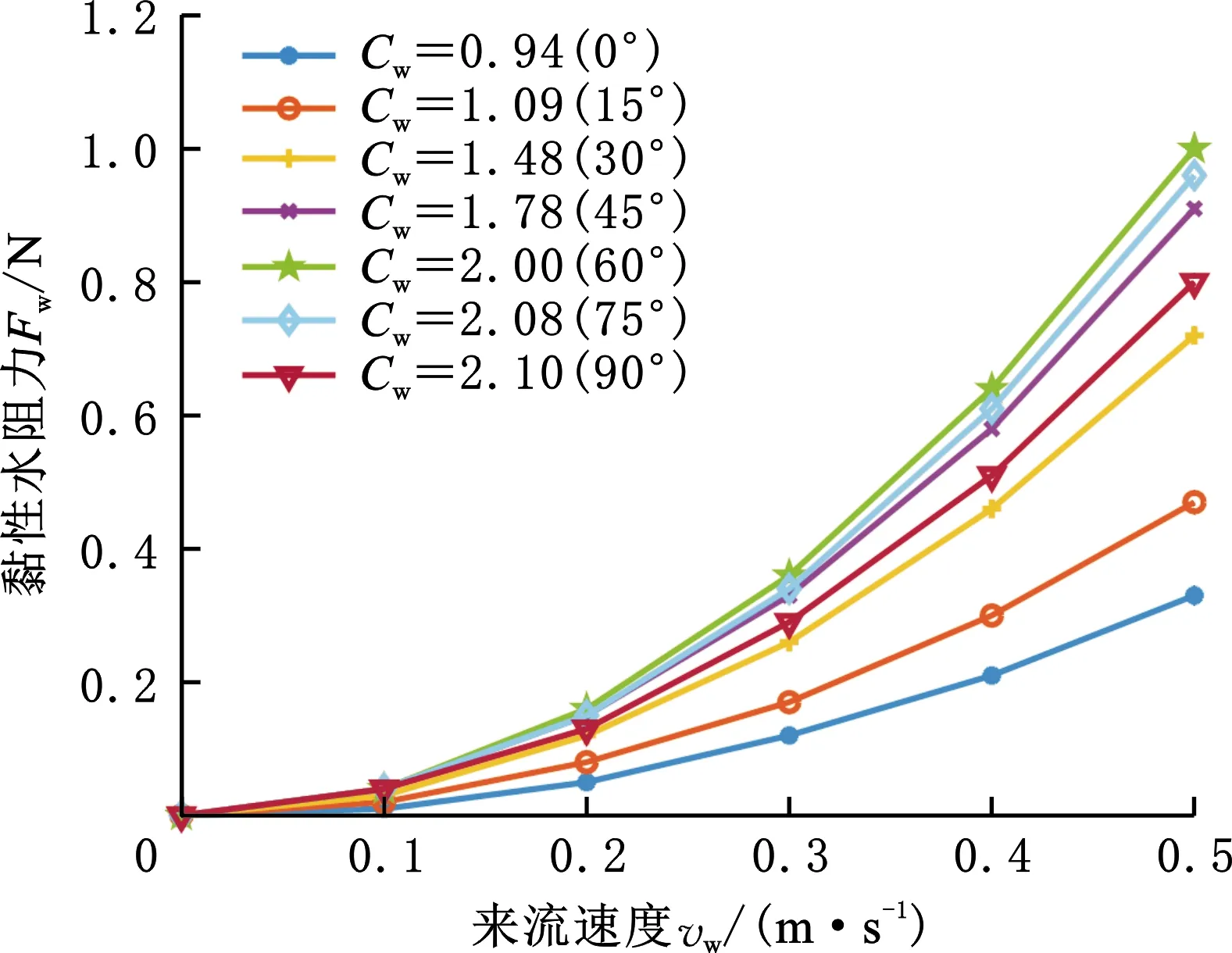
图14 黏性水阻力拟合曲线Fig.14 Viscous hydrodynamic fitting curve

为了确定履带装备模型的水阻力与外形的关系，将履带装备模型简化为规则的立方体，如图12所示，则履带装备模型的迎水横截面积可以表示为

Am=(Lsinθ+bcosθ)h

(3)

其中，L为履带装备模型的长度；b为履带装备模型的宽度；h为履带装备模型的高度。设置履带装备模型的前进速度为0.5 m/s，对不同来流角度的水阻力值进行拟合，如图15所示，得到来流角度和黏性水阻力系数的关系：

Cw=1.25sinθ+0.87

(4)

图15 水阻力系数拟合曲线Fig.15 Hydrodynamic coefficient fitting curve

拟合曲线的和方差为0.02，确定系数R2为0.97，说明函数可以较好地反映水阻力系数的变化趋势。根据来流角度和黏性水阻力系数的关系，水下履带装备模型的黏性水阻力Fw的经验公式为

Fw=0.5(1.25sinθ+0.87)ρw(Lsinθ+bcosθ)·

h|vw-v|(vw-v)

(5)

3 姿态识别及水阻力计算验证

以试验和仿真数据总结的规律作为先验，应用于水下履带装备模型的姿态识别与水阻力估计。在试验验证中，将履带车模型的行进速度设置为0.45 m/s，履带装备模型的来流角度设置为40°，如图16所示。

图16 试验验证示意图Fig.16 Schematic diagram of experimental verification

采集履带装备模型的12个侧线数据点数值作为测试组，压力分布如图17所示。由相关性系数检测可知，测试组的压力分布与来流角度为45°、来流速度为0.5 m/s时的数据最为相似，相关系数分别为0.98和0.94。将水流流速代入式(6)，计算履带装备模型的黏性水阻力为0.83 N，水阻力验证试验的平均黏性水阻力为0.71 N，则相对误差为17%。

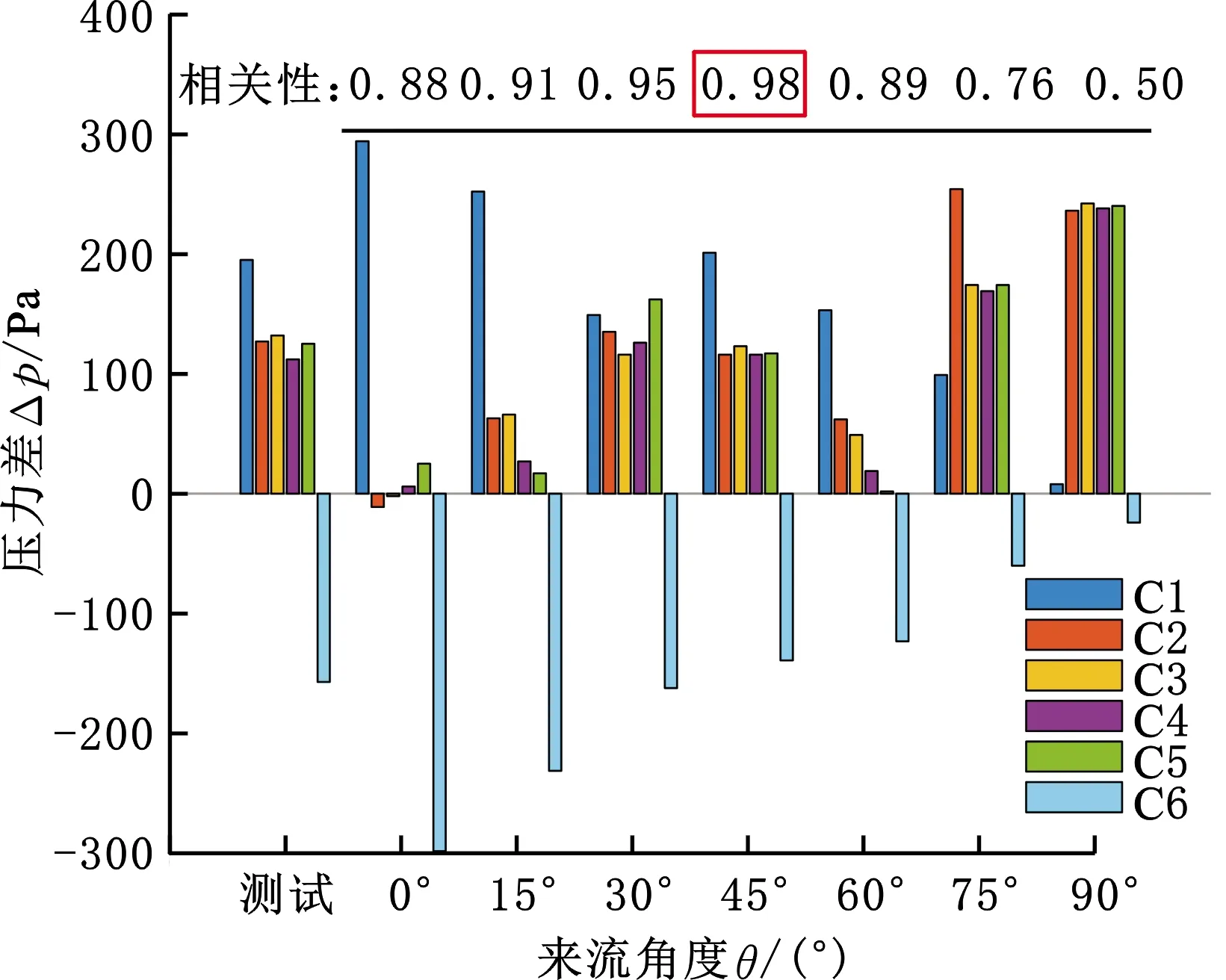
(a)来流角度相关性检测

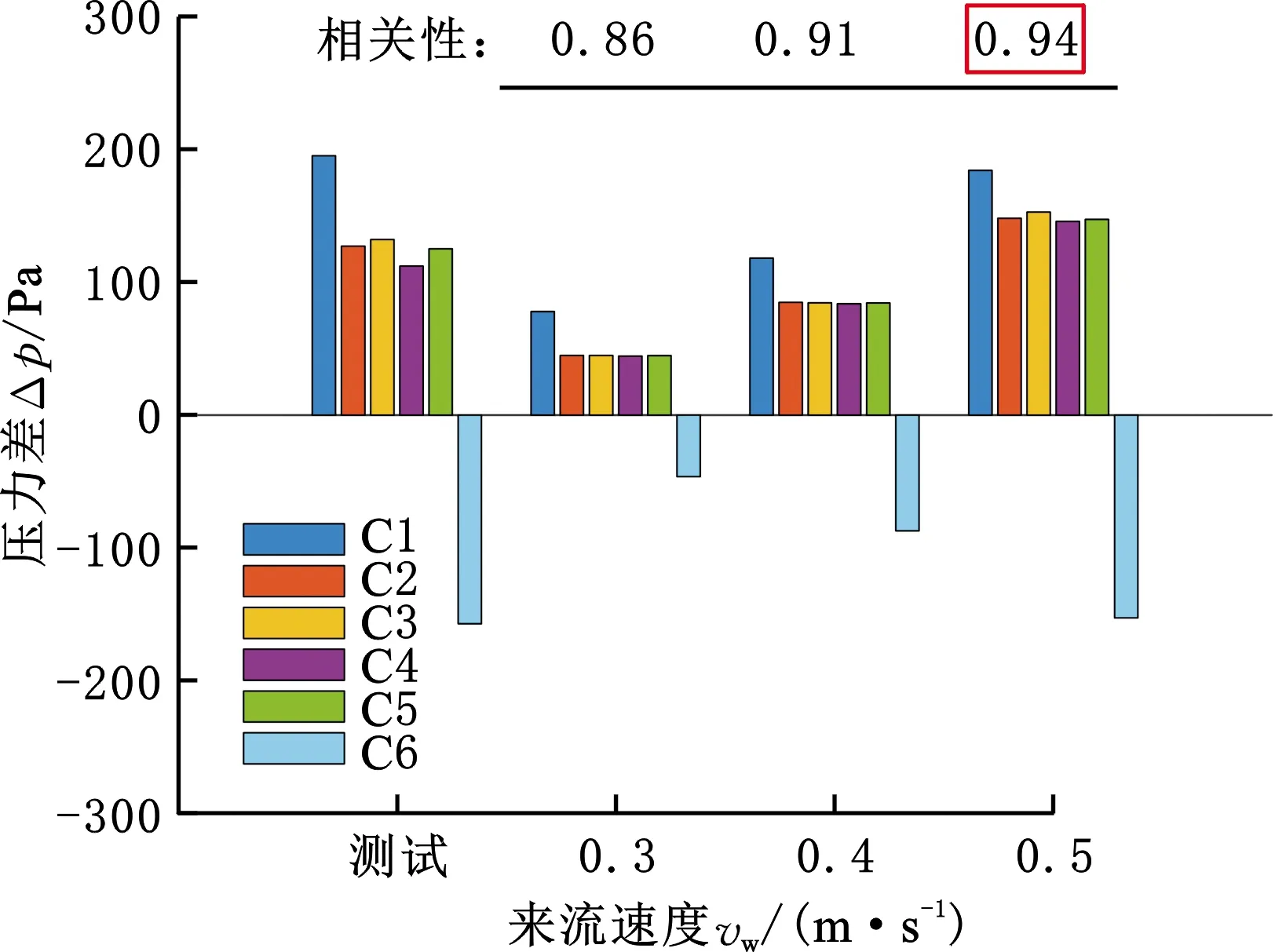
(b)来流速度相关性检测图17 测试组相关性系数Fig.17 Test group correlation coefficient

4 结论

(1)将人工侧线系统应用于水下履带装备，通过采集履带装备表面压力数据，根据压力分布的相关性检测可以有效感知履带装备模型的局部来流速度和来流角度。

(2)建立履带装备迎流面外形与黏性水阻力系数的函数关系，推导得到水下履带装备的黏性水阻力的经验模型。

(3)提出水下履带装备的水阻力实时估算方法。应用人工侧线的流场感知结果，作为水阻力计算的输入，估算不同迎流姿态的履带装备水阻力，测试误差为17%，满足工程需要。