一种无监督的轴承健康指标及早期故障检测方法

赵志宏 李乐豪 杨绍普 李 晴

1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄，0500432.石家庄铁道大学信息科学与技术学院，石家庄，050043

0 引言

随着传感器和通信技术的不断发展，轴承状态检测系统会采集到海量的监测大数据，这些监测大数据中蕴含着关于轴承健康状态的信息。如何利用这些监测大数据实现轴承故障预测与健康管理(prognostics and health management，PHM)对提升机械装备的可靠性具有重要意义[1]。

目前，针对机械部件的PHM技术主要包括状态实时监控[2-3]、故障检测与隔离[4-5]和剩余使用寿命预测[6-7]等。其中，构建能够反映机械部件健康状态、量化退化趋势的健康指标是PHM中的重要问题。随着智能诊断技术需求的不断增加，很多专家使用机器学习方法将人工提取的多个特征进行降维及融合，从而构建能够反映时域、频域和时频域上变化规律的健康指标。如QIU等[8]利用小波滤波器对振动信号进行降噪后提取峭度、均方根等多种特征，再使用自组织神经网络(self organizing maps，SOM)融合特征构建健康指标，实现了轴承的健康状态监测。张全德等[9]使用主成分分析和SOM进行特征融合，获取了可以反映轴承劣化趋势的健康指标。YANG等[10]使用SOM融合特征构建健康指标，并引入缩放参数统一失效阈值，通过粒子滤波器预测剩余使用寿命。相比峭度、均方根等单一指标，以上方法在一定程度上提高了泛化能力，但仍需手工选取特征，依赖专家经验。

自HINTON等[11]提出深度学习理论后，深度神经网络以其强大的特征自提取能力影响了很多领域的发展。一些学者使用深度神经网络构建健康指标，按照训练神经网络时是否需要标注信息分为有监督方法和无监督方法，有监督健康指标构造方法常常使用卷积神经网络或长短时记忆网络搭建模型。王久健等[12]提出了一种空间卷积长短时记忆神经网络的健康指标构建方法，对轴承的剩余使用寿命进行预测。孙世岩等[13]将时域特征、频域特征和时频图送入多输入神经网络中获取健康指标，获取的健康指标具有较好的趋势性、单调性和离散性。CHEN等[14]将振动信号输入由卷积神经网络和长短时记忆单元构成的神经网络中获取健康指标，对轴承退化过程进行表征。这些有监督方法需要给训练集不同时刻的数据根据运行时间打上[0，1]之间的标签以代表健康程度，虽然可在一定程度上表示轴承的退化趋势，但是并不能较好地反映轴承退化的不同阶段。无监督方法则是根据退化特征的变化规律建立健康指标，与有监督方法建立的健康指标相比，无监督方法建立的健康指标能反映轴承退化的不同阶段，可以用来表示轴承非线性的退化过程。佘道明等[15]使用深度自编码器提取轴承全寿命的退化特征，然后从中选取趋势性较好的特征构建健康指标，并对轴承的退化过程进行建模。尹爱军等[16]使用变分自编码器提取轴承频谱特征，建立了基于状态概率分布和重构误差的健康指标，通过健康指标实现了轴承的健康状态评估。毛文涛等[17]提出一种多域迁移自编码器提取轴承特征，计算轴承特征的排列熵从而得到健康指标，借助离线数据获取报警阈值实现了早期故障检测。

当前研究主要是利用健康指标对轴承的退化趋势进行建模或者预测完全失效时间，利用健康指标进行早期故障的研究报道较少。为解决轴承健康评估问题，本文提出了一种基于深度可分离卷积自编码器的无监督健康指标构建及早期故障检测方法，离线阶段训练深度可分离卷积自编码器，获得可以提取轴承全寿命不同阶段特征的编码器，在线阶段计算当前时刻退化状态特征与健康状态特征之间的Bray-Curtis距离获得健康指标BC-HI，在BC-HI上使用Savitzky-Golay滤波动态平滑的故障检测方法判断当前轴承的故障情况。

1 无监督特征提取模型

1.1 自编码器

自编码器的结构如图1所示，由编码器和解码器组成，其编码和解码过程可描述为

h=fe(Wex+be)

(1)

y=fd(Wdh+bd)

(2)

其中，x代表输入数据；h代表隐藏层特征；y代表重构数据；We、Wd代表权值矩阵；be、bd代表偏置；fefd代表激活函数。经过训练后h即为自编码器提取到的特征。自编码器的训练过程可以描述为最小化一个损失函数L(x，y)。

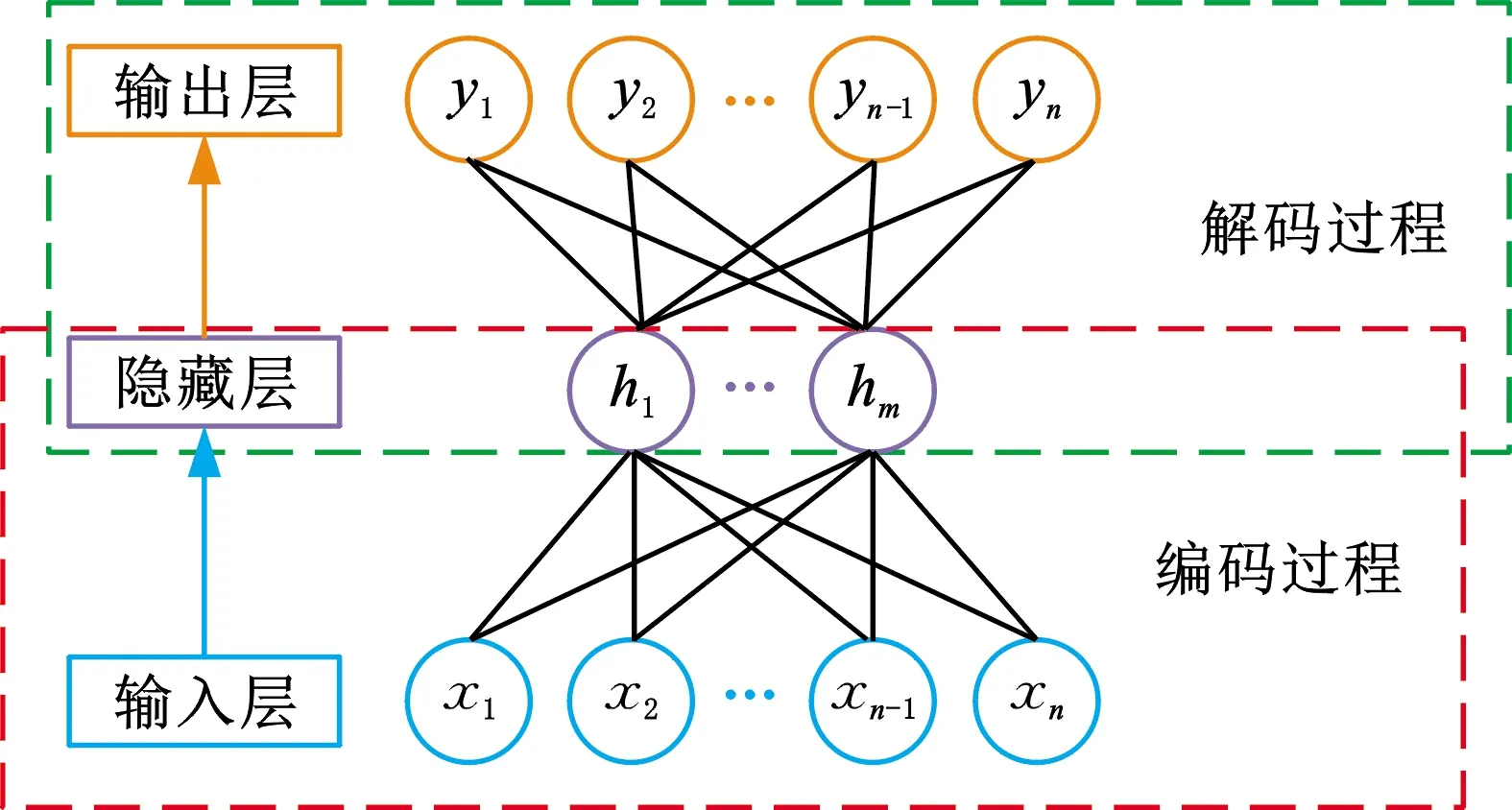
图1 自编码器的网络结构Fig.1 Structure of auto-encoder

1.2 深度可分离卷积

图2 深度可分离卷积结构Fig.2 Structure of depthwise separable convolution

深度可分离卷积[18]是对传统卷积的改进，可以在保证特征提取能力的前提下有效降低计算量和参数量，针对一维信号的深度可分离卷积的结构如图2所示，由深度卷积(depthwise convolution，DWC)和逐点卷积(pointwise convolution，PWC)两部分组成。在深度卷积中，M个深度卷积核分别对M个输入特征进行卷积运算，M个卷积对应M个通道，通道之间没有关联，通过深度卷积可以得到M个特征。由于深度卷积每个通道的计算都是独立进行的，没有利用不同通道相同位置上的特征信息，故需要逐点卷积对这些特征进行融合。逐点卷积的运算方式与传统卷积是一致的，只是卷积核的大小为1×1，通过逐点卷积可以对深度卷积运算得到的特征进行加权融合。在深度可分离卷积中，可以通过在深度卷积中设置步长和在逐点卷积中设置通道数来控制特征的缩小或扩大。

1.3 深度可分离卷积自编码器模型

本文提出一种可以提取轴承健康状态特征的深度可分离卷积自编码器，其网络结构如图3所示，编码器由3个深度可分离卷积组成，在深度卷积和逐点卷积后添加了ReLU激活函数和批标准化(batch normalization，BN)，ReLU激活函数可以使负值置零，具有较强的非线性能力[19]，BN可以加速训练，避免梯度爆炸[20]；解码器同样也由3个深度可分离卷积组成，不同的是将深度卷积替换为深度转置卷积(depthwise transposed convolution，DWTC)进行数据重构。

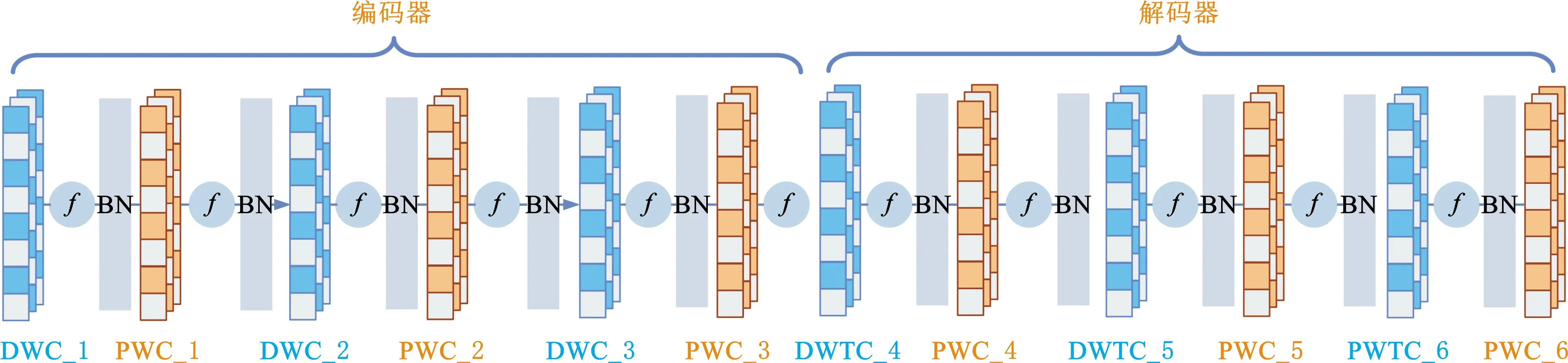
图3 深度可分离卷积自编码器网络结构Fig.3 Network structure of deep separable convolutional auto-encoder

深度可分离卷积自编码器的网络参数见表1，编码器中通过对深度卷积设置步长，每次深度卷积运算后都减少了特征的长度，最后编码器提取到的特征尺寸为10×20；解码器通过深度转置卷积不断扩大特征的尺寸，最后一层逐点卷积时，将多个特征加权融合。如果使用传统卷积替换深度可分离卷积构建卷积自编码器，在各个网络层的输入与输出尺寸与深度可分离卷积自编码器相同的情况下，参数量为28.650M，计算量为79.795k，而深度可分离卷积自编码器的参数量仅为4.097M，计算量仅为9.960k，分别减少了85.7%和87.5%。

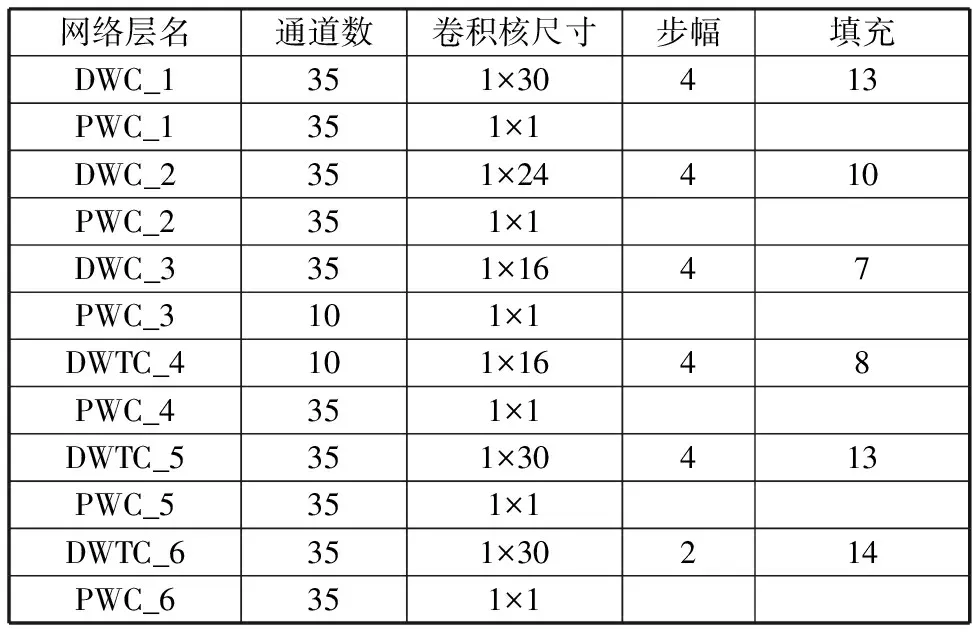
表1 深度可分离卷积自编码器网络参数Tab.1 Network parameters of deep separable convolutional auto-encoder

2 健康指标构建及早期故障检测方法

2.1 无监督健康指标构建方法

无监督构建健康指标的流程如图4所示，分为离线和在线两个阶段，离线阶段获取特征提取模型，在线阶段获取健康指标。离线阶段的具体步骤如下：

(1)采集轴承全寿命振动加速度信号。

(2)对每段振动信号进行频谱变换，取每段频谱前1280个频率点作为训练样本构建训练集。

(3)使用训练数据集对深度可分离卷积自编码器进行训练，优化器为Adam，损失函数为

(3)

(4)

其中，损失函数由smoothL1损失函数和L2正则化组成，n为输入数据所包含频率点的个数，y(k)为重构数据第k个频率点的幅值，x(k)为输入数据第k个频率点的幅值，λ为L2正则化系数，m为神经网络中权重的数量，wk为神经网络的第k个权重。与L1损失函数相比，smoothL1损失函数可以让模型收敛更快且不容易受离群点和异常值的干扰。L2正则化可以避免权值矩阵过大导致的输入微小变化而引起的特征值的较大改变，从而提高泛化能力。

(4)当损失不再下降时停止训练，得到可以有效提取特征的编码器。

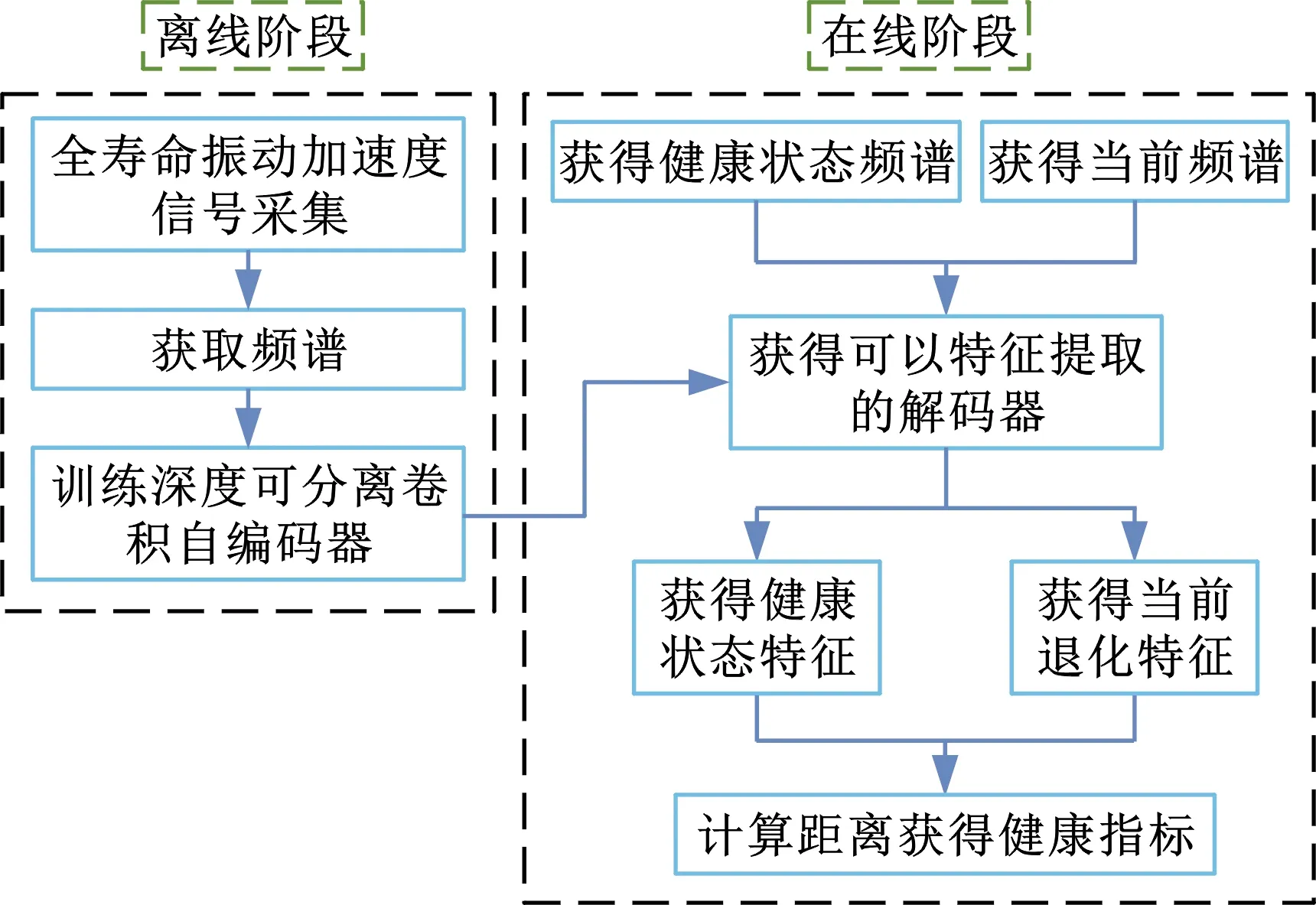
图4 健康指标构建流程图Fig.4 Flow chart of health indicator construction

在线阶段获取健康指标的具体步骤如下：①将轴承初始时刻的频谱输入编码器中得到健康状态特征；②将当前时刻的频谱输入编码器中得到退化状态特征；③计算退化状态特征与健康状态特征之间的Bray-Curtis距离，以该距离作为健康指标。

Bray-Curtis距离[21]是生态学常用的度量指标，可以根据物种组成计算两个生物群落之间的相似度。Bray-Curtis距离计算时，不仅考虑物种的有无，还考虑了不同物种的相对丰度[22]。对应轴承健康指标构建问题，Bray-Curtis距离则可以衡量健康状态特征和退化状态特征之间对应特征值的有无及大小差异，同时具有将差异程度归一化的特点，消除了量纲的影响，与欧氏距离相比，受特征值大小的影响较小[23]，其计算方式如下：

(5)

式中，xik为健康状态特征的第k个特征值；xjk为退化状态特征的第k个特征值。

该距离的取值在[0，1]之间，越接近0表示两个特征之间的差异越小，轴承越健康；越接近1表示两个特征之间的差异越大，轴承越接近完全失效。

2.2 早期故障检测方法

根据本文所提健康指标的特点和3σ准则，健康指标的异常阈值设置为正常值与3倍标准差之和。为减少噪声引起的误报，使用Savitzky-Golay滤波器对当前健康指标进行平滑，提出一种Savitzky-Golay滤波平滑的基于3σ准则的在线早期故障检测方法，在线检测流程如图5所示，获取一个新的健康指标后，故障检测的具体步骤如下。

(1)将当前获取的健康指标BC-HI插入健康指标序列BC-HIS中。

(2)使用Savitzky-Golay滤波器对BC-HIS进行滤波处理，得到较为平滑的健康指标序列。

(3)计算BC-HIS中健康状态的均值μheal和标准差σheal。

(4)计算轴承异常状态阈值T：

T=μheal+3σheal

(6)

(5)如果平滑后的BC-HI大于异常阈值T则检测为故障，反之则检测为健康。

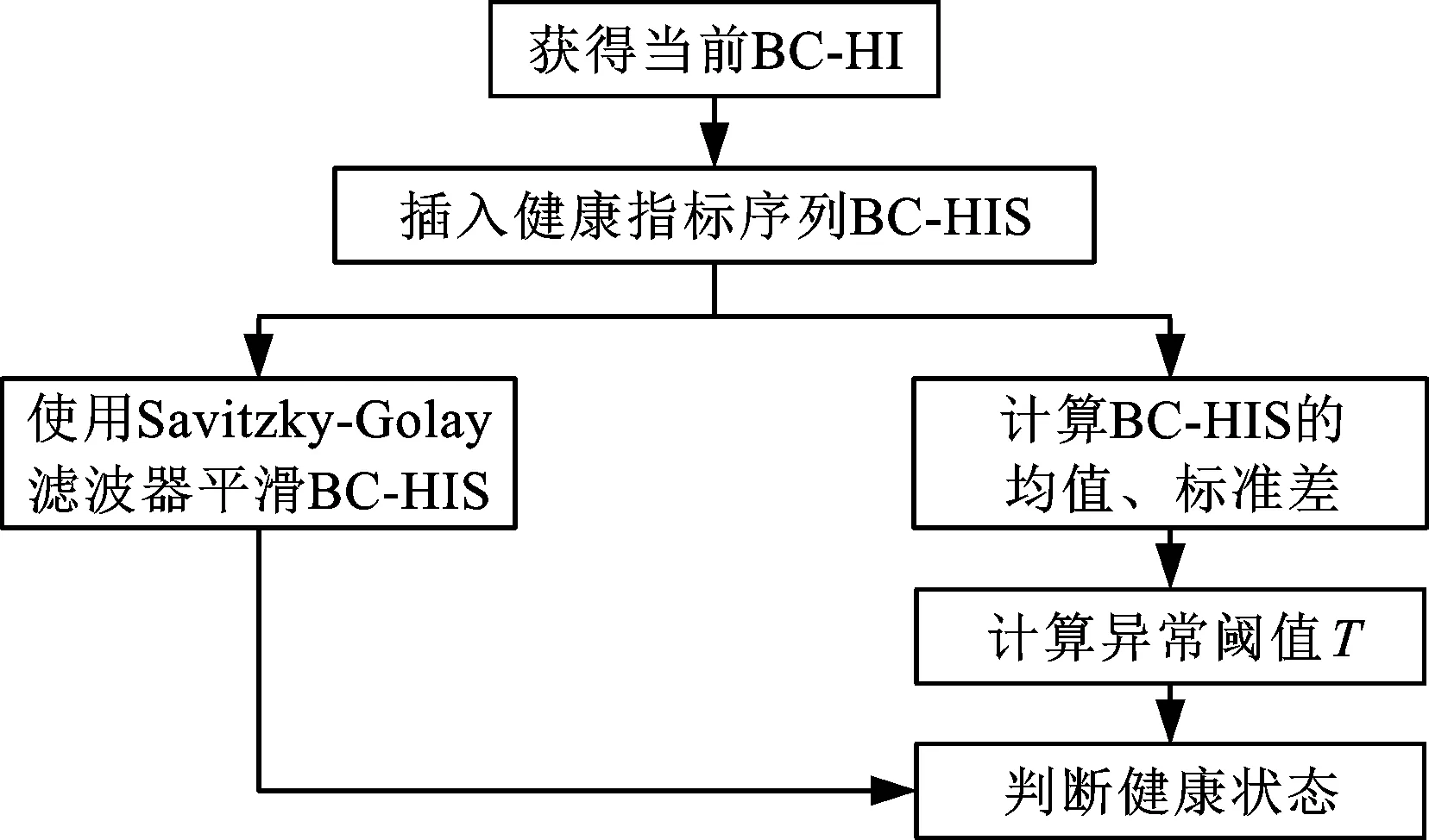
图5 早期故障检测流程图Fig.5 Flow chart of early fault detection

通过本文提出的Savitzky-Golay滤波平滑的基于3σ准则的在线早期故障检测方法，可以根据待评估轴承的健康指标序列计算异常阈值，无需手工设置。在轴承运行过程中，故障的发生往往伴随着频谱成分的改变，反映在健康指标上则是突然的大幅增长，该增长会被3σ准则判断为粗大误差，从而检测出故障；而健康指标上较小的波动很有可能是由噪声引起的，通过Savitzky-Golay滤波可以使该波动平滑，从而降低误报率。

3 试验验证

3.1 数据集

本文使用XJTU-SY滚动轴承加速寿命试验数据集[24]进行验证，轴承加速寿命测试平台由交流电动机、电动机转速控制器、转轴、支撑轴承、液压加载系统和测试轴承组成，如图6所示。测试轴承为LDKUER204滚动轴承，数据集组成见表2，共有3种工况：工况1转速为2100 r/min、径向力为12 kN，工况2转速为2250 r/min、径向力为11 kN，工况3转速为2400 r/min、径向力为10 kN。每种工况下加工5个轴承，采样频率为25.6 kHz，采样间隔为1 min，每次采样时长为1.28 s。

图6 试验台Fig.6 Experiment rig

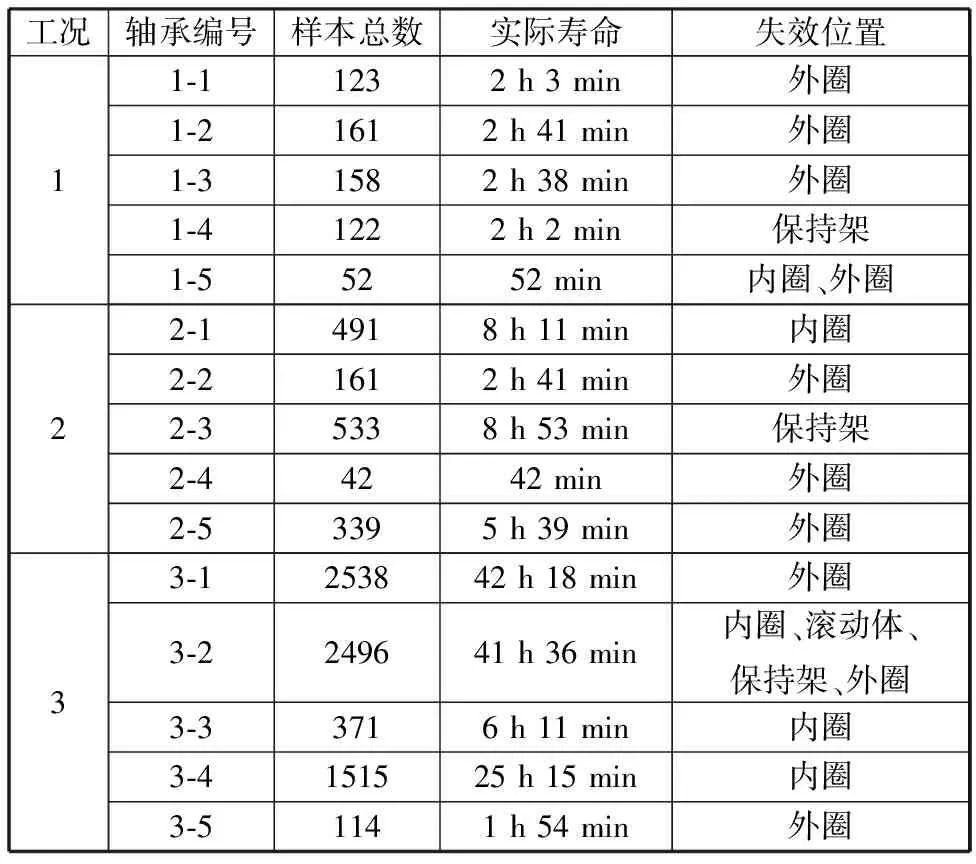
表2 XJTU-SY轴承数据集

3.2 健康指标试验与分析

3.2.1试验设置

由于试验室环境与真实的工业场景有一定的差异，对负载和转速不敏感的方法更有可能应用于实际工程中，故一个应用价值较高的健康指标构建及早期故障检测方法应具有较好的泛化性能。为测试本文方法的泛化性能，深度可分离卷积自编码器模型的训练和测试分别在不同工况下进行。在训练阶段，使用工况3下5个轴承的全寿命周期数据作为训练集；在测试阶段，使用工况1和工况2下10个轴承的全寿命周期数据作为测试集在线进行健康指标构建和早期故障检测试验，检验本文方法的有效性和泛化能力。

离线训练时卷积核大小、通道数、学习率和L2正则化系数等参数取值参考相关文献确定大致范围，然后利用网格搜索法进行搜索，经过试验确定最终参数取值，批量大小为200，迭代次数为2000，初始学习率为5×10-4，L2正则化系数为1.2×10-5，经过1000轮训练后学习率减小为4×10-4。

为验证Bray-Curtis距离更适合用来量化轴承退化趋势，与常用的欧氏距离方法和相关系数方法得出的健康指标进行对比。计算退化状态特征与健康特征的距离时使用欧氏距离或相关系数来获取健康指标，并与Bray-Curtis距离获取的健康指标进行单调性和趋势性对比。单调性可以评估单调上升或单调下降的趋势，其计算公式为

(7)

式中，H为健康指标序列；Npos为对时间求导后导数值大于0的健康指标数量；Nneg为对时间求导后导数值小于0的健康指标数量；K为健康指标总个数。

趋势性可以评估健康指标和运行时间的相关性，其计算公式为

(8)

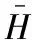
3.2.2健康指标试验

离线训练阶段前25代的损失曲线如图7所示，可以看到损失值收敛速度较快，在前25代时已收敛至较低水平，在经过2000代训练后最终的损失值为1.62×10-5。

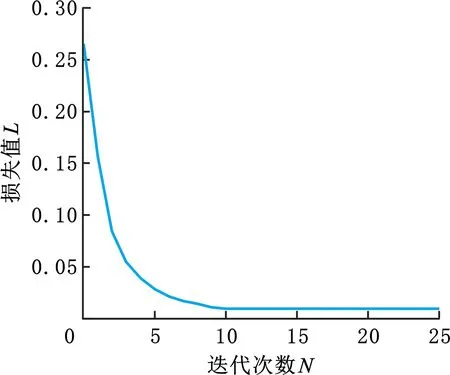
图7 损失曲线Fig.7 Loss curve

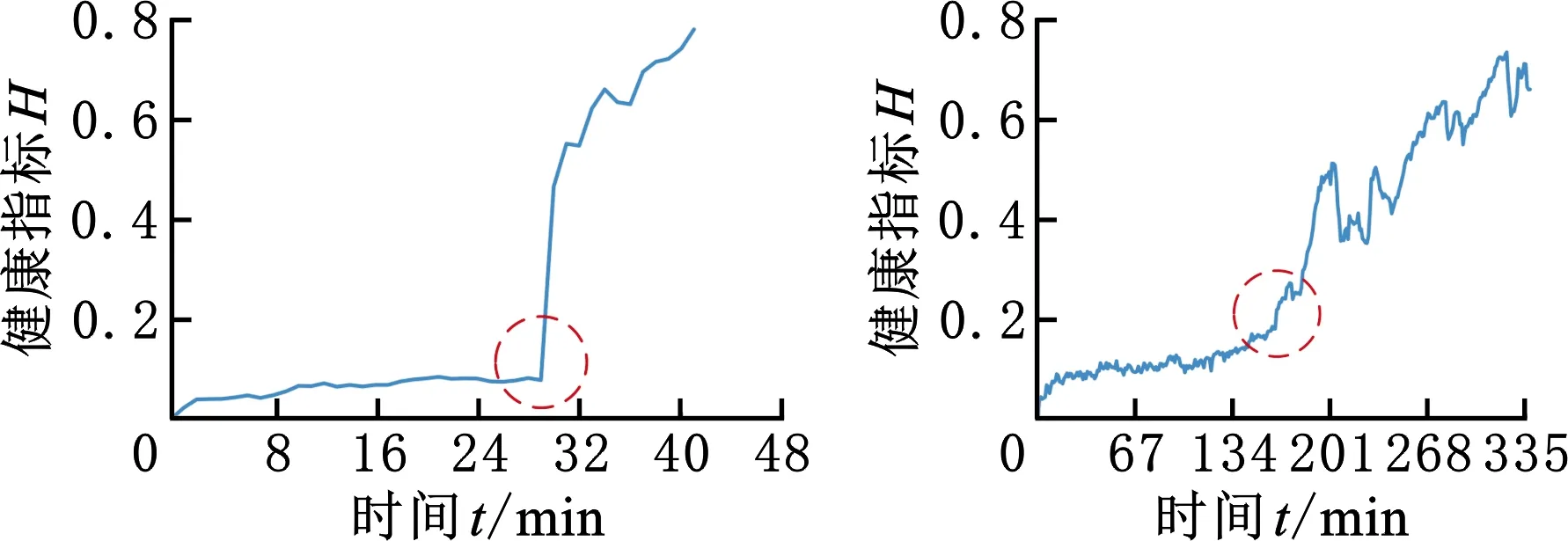
在线测试阶段，工况1和工况2下10个轴承的健康指标如图8所示，可以看到获取的健康指标单调性较好，长期趋势均为递增，可以反映轴承退化至完全失效的趋势，并且测试轴承在运行到某个阶段时都会出现健康指标突然增大的情况。

使用欧氏距离和相关系数获取测试集的健康指标，计算平均单调性和平均趋势性，并与本文基于Bray-Curtis距离获取的健康指标对比，对比结果见表3，可以看到基于Bray-Curtis距离的健康指标单调性和趋势性均优于欧氏距离和相关系数，可以更好地反映轴承随着运行时间增加故障程度逐渐加深的过程。

3.2.3试验分析

以轴承1-1和轴承1-3为例分析健康指标突然增大的原因，在工况1下轴承的外圈故障频率理论值为107.91 Hz。轴承1-1部分时刻频谱如图9a～图9c所示，对比图9a和图9b可以看到第1 min的频谱和第78 min的频谱虽然成分有所改变，但是频谱峰值相差不大，在图9c中第79 min频谱峰值突然增大，可以找到近似外圈故障2倍频的217 Hz、3倍频的326 Hz和10倍频的1087 Hz等成分，并且1087 Hz成分为峰值，可以表明第79 min轴承1-1发生了早期故障。轴承1-3部分时刻频谱如图10a～图10c所示，其变化规律与轴承1-1相似，第1 min和第58 min的频谱相似程度很高，第59 min时峰值突然增大，可以找到近似外圈故障1倍频的108 Hz、2倍频的219 Hz、3倍频的328 Hz等成分，可以表明第59 min时轴承1-3发生了早期故障。从上述分析中可以发现本文所提健康指标对早期故障较为敏感，早期故障的发生可以体现在健康指标的突然增大，因此通过监测所提健康指标在短时间内突然增大的情况来实现早期故障检测，具有一定的可行性和有效性。

(a)轴承1-1 (b)轴承1-2 (c)轴承1-3 (d)轴承1-4

(e)轴承1-5 (f)轴承2-1 (g)轴承2-2 (h)轴承2-3

(i)轴承2-4 (j)轴承2-5图8 测试轴承的健康指标Fig.8 Test bearing health indicators

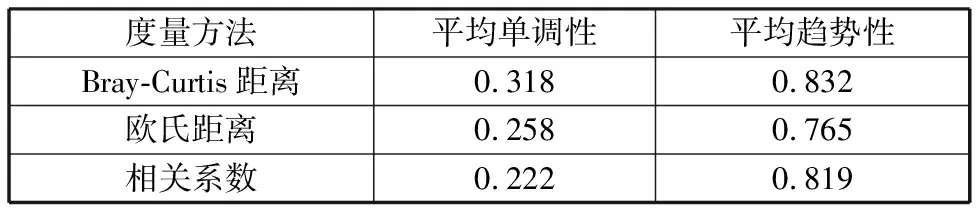
表3 不同度量方法的单调性和趋势性对比Tab.3 Monotonicity and trend comparison of different measurement methods

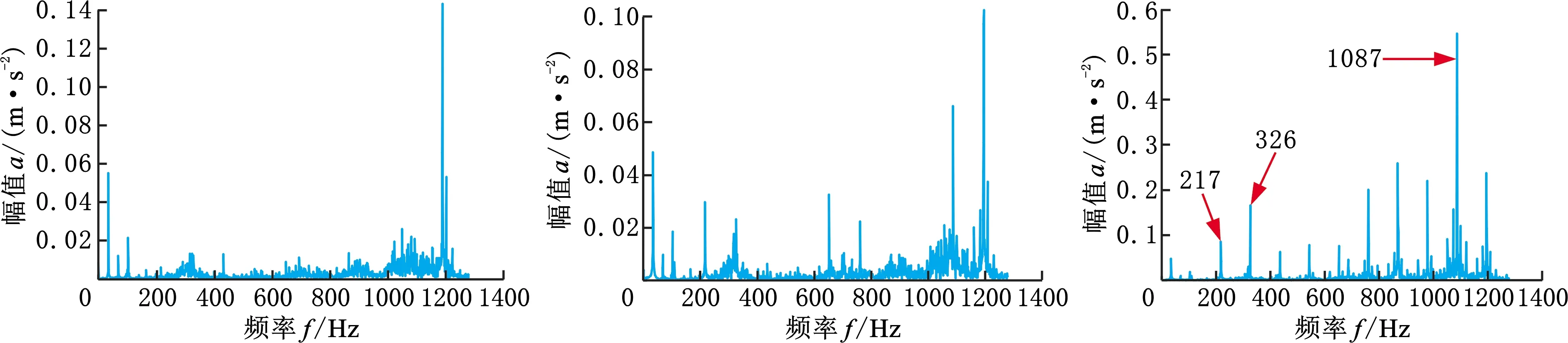
(a)第1 min (b)第78 min (c)第79 min图9 轴承1-1部分时刻频谱Fig.9 Bearing 1-1 part of the time frequency spectrum

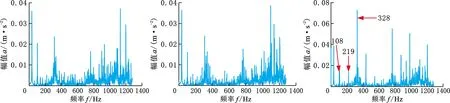
(a)第1 min (b)第58 min (c)第59 min图10 轴承1-3部分时刻频谱Fig.10 Bearing1-3 part of the time spectrum

(a)第1 min (b)第78 min (c)第79 min (d)第80 min图11 轴承1-1不同时刻提取到的特征Fig.11 Feature extraction of bearing1-1 at different time

对深度可分离卷积自编码器提取轴承1-1不同时刻的特征进行可视化，可视化方法为将尺寸为10×20的状态特征铺平为1×200的一维数据，可视化结果如图11a～图11d所示，可以看出深度可分离卷积自编码器提取的特征可以反映轴承频谱的变化，轴承1-1的第1 min频谱和第78 min的频谱比较相似，第1 min的健康状态特征与第78 min的退化状态特征也比较相似，从第79 min开始退化状态特征出现非常明显的变化，同时可以看到特征值都比较小，这是由于L2正则化起了作用，使网络中的权值尽可能小，增强了抗干扰能力，提升了模型的泛化性能，使得模型在测试集与训练集工况不同的情况下仍然可以有效提取特征。

3.3 在线早期故障检测试验与分析

使用本文提出的早期故障检测方法在测试集健康指标上进行早期故障检测，测试集中各个轴承的全寿命周期检测结果如图12所示，其中棉棒图顶端为1表示健康，顶端为0表示故障，可以看到不管是在工况1还是工况2下，本文方法均对健康指标首次突然增大的点进行了报警，在此之前不存在误报，验证了所提早期故障检测方法的有效性。

为进一步验证所提方法的优势，表4给出了所提方法与文献[17]以及两种经典的无监督异常检测方法首次故障时间和误报警数对比，两种无监督异常检测方法的实现细节如下。

(a)轴承1-1 (b)轴承1-2 (c)轴承1-3 (d)轴承1-4

(e)轴承1-5 (f)轴承2-1 (g)轴承2-2 (h)轴承2-3

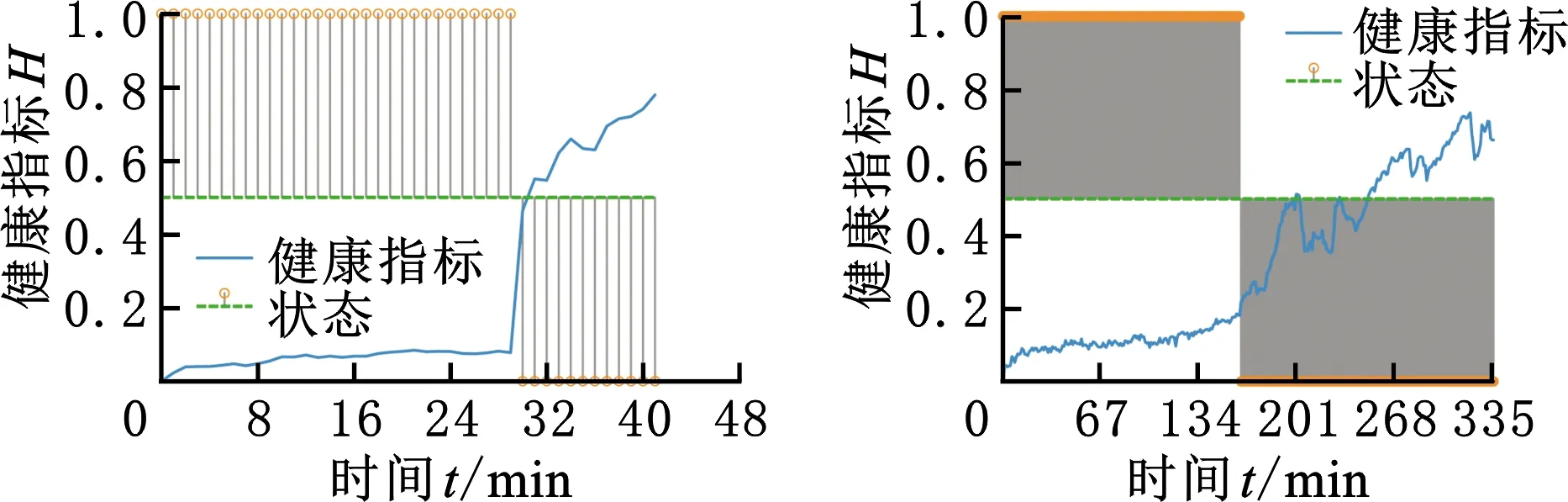
(i)轴承2-4 (j)轴承2-5图12 测试轴承上的检测结果Fig.12 Detection result on test bearings

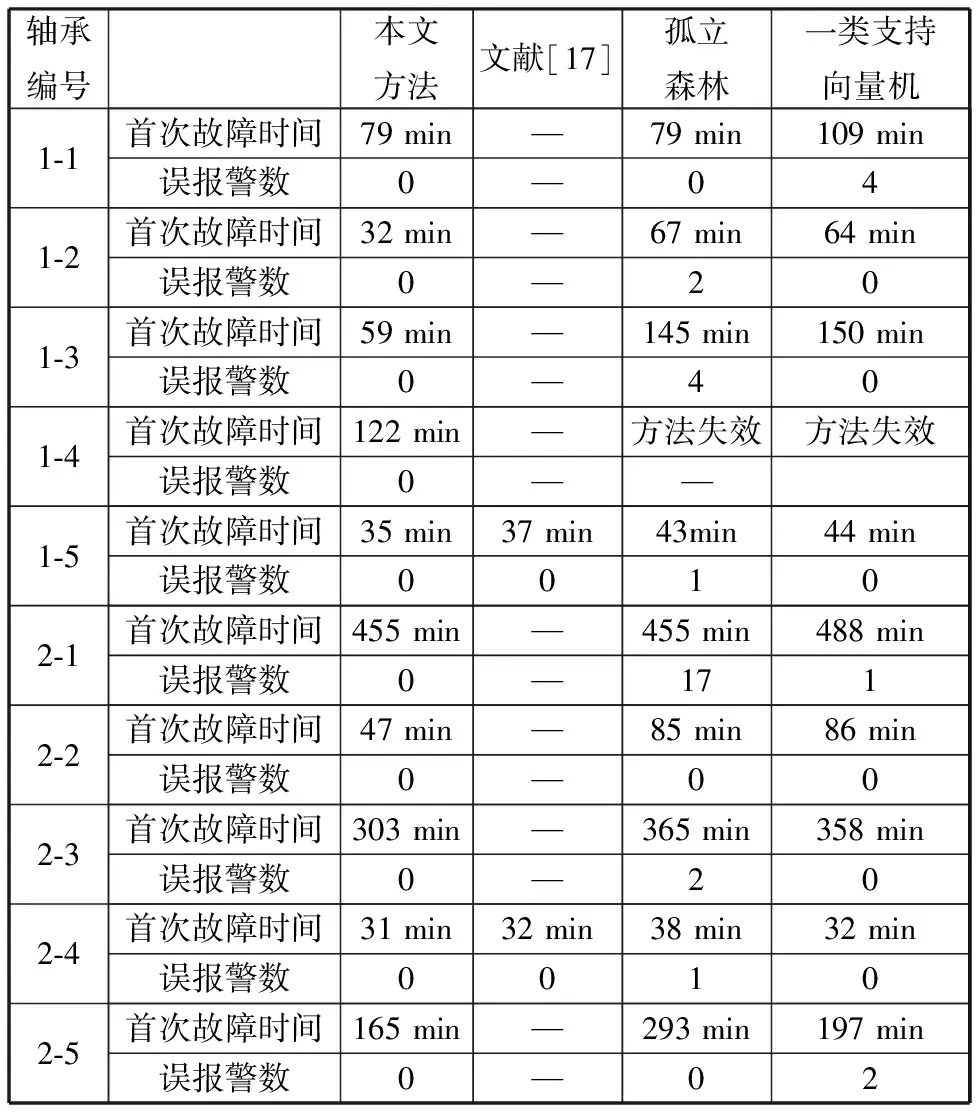
表4 四种方法检测结果对比Tab.4 Comparative detection results of four methods

孤立森林[25]：该方法是一种经典的异常检测方法，其基本思想是使用超平面对数据集空间进行多次切割，直到每个子空间只剩一个样本点，切割所需次数越少越可能是异常数据。孤立树的数量为100，构建孤立树所需的最大数据点数为256，使用深度自编码器提取特征进行检测，编码器的维度变化为1280—800—500—200。

一类支持向量机[26]：该方法是一种用于解决样本极度不平衡的分类方法，常用于无监督异常检测问题，其基本思想是通过核函数映射将样本映射到高维特征空间中，在高维空间中构造线性判别函数来实现异常检测。核函数为径向基核函数，使用深度自编码器提取的特征进行检测，编码器的维度变化为1280—800—500—200。

在试验中如果连续3次检测出异常，则可认定为发生故障，否则按误报警处理。本文方法和对比方法在测试集上的检测结果见表4，本文方法和文献[17]方法均不存在误报警，与文献[17]方法相比，本文方法的首次故障时间更提前，同时孤立森林方法和一类支持向量机方法均存在误报的情况，首次故障时间也存在较大的延后，可以看到本文方法与其他方法相比具有一定的优越性。

使用深度可分离卷积自编码器对测试集10个轴承进行全寿命周期的健康指标构建和早期故障诊断，总用时约39.71 s，样本总数为2182，每个样本构建健康指标和进行早期故障的用时约为0.018 s，用时较短，可以反映出深度可分离卷积轻量级的特点，同时也表明本文方法满足实时状态监测时效性的需求，适用于轴承的实时状态监测。

4 结论

(1)深度可分离卷积自编码器可以有效提取轴承健康状态特征，相比传统卷积自编码器，其参数量和计算量更少，适用于轴承的实时状态监测。

(2)与欧氏距离、相关系数相比，Bray-Curtis距离构建的健康指标具有更好的单调性与趋势性。

(3)本文提出的健康指标BC-HI可以较好地反映轴承退化趋势，并且对早期故障较为敏感。

(4)基于BC-HI的早期故障检测方法无需人工设置异常阈值，与孤立森林、支持向量机方法相比，首次故障时间更加提前，误报警数更少。

下一步的研究工作为使用所提健康指标进行轴承首次故障时间的预测，并在其他机械设备上进行试验。