基于任务参数加权的动态运动基元泛化方法
张 磊 方灶军 王聚幸 何 晨 顾丹宁
1.中国科学院宁波材料技术与工程研究所,宁波,3152012.中国科学院大学,北京,1000493.浙江省机器人与智能制造装备技术重点实验室,宁波,315201
0 引言
在不久的将来,机器人将成为人类社会不可或缺的一部分,在教育、医疗、家庭、灾害场景及太空探索等领域为人们提供协助。机器人将不仅在结构化环境下执行单一任务,而是会面临非结构化复杂环境下的多变任务。为所有场景和任务都进行传统的示教编程是非常耗时耗力的,因此,机器人需要依靠自身的学习能力完成相应任务[1]。
传统的机器人示教编程类似于简单的“复制粘贴”操作,对某一特定场景下的特定任务进行示教,机器人只能在该场景下完成对应任务,若场景或任务条件稍有变化,任务便不能完成,需要对机器人重新示教。而机器人示教学习(learning from demonstration,LfD)通常也称作机器人模仿学习(imitation learning),运用机器学习的方法使机器人学习示教者的动作技巧从而掌握新的任务技能。与传统机器人示教编程相比,LfD具有泛化能力,在场景和任务与示教不同的情况下,机器人仍然能凭借从示教过程中学习到的动作技巧和特征完成任务。
针对单条运动轨迹的示教学习,IJSPEERT等[2]提出了一种基于动态运动基元(dynamic movement primitive,DMP)的轨迹编码方法,能够将示教运动轨迹的形状特征以特征参数的形式保存,对于一个新的任务场景,可以通过学习到的特征参数重构一条包含示教者运动特征的运动轨迹。针对多条运动轨迹的示教学习,在DMP的基础上,UDE等[3]首先使用高斯过程回归(Gaussian process regression,GPR)求出任务参数到DMP运动轨迹目标点g与时间缩放量τ的映射,其他模型参数固定为常数;然后使用局部加权回归(locally weighted regression,LWR)基于所有示教运动轨迹的非线性项计算出新的特征参数,最后根据新的特征参数重构新的运动轨迹。刘环等[4]首先使用LWR计算出所有示教运动轨迹对应的DMP特征参数,对于一个新的任务参数,基于计算得到所有的特征参数,使用高斯过程回归求出相应的新的特征参数,最后重构新的运动轨迹。
以上两种泛化方法存在计算效率不高以及在示教任务参数附近的泛化性能差等问题。本文提出了一种基于任务参数加权的动态运动基元泛化方法。首先对于每条示教运动轨迹,使用局部加权回归计算出对应的特征参数;对于一个新的任务,由各条示教运动轨迹学习到的特征参数计算出在新的任务参数处的特征运动轨迹;基于示教任务参数与新的任务参数的相似度给予各条特征运动轨迹不同的权重,然后对各条特征运动轨迹进行加权叠加形成新的运动轨迹;对动态运动基元及常用的泛化方法进行介绍,并重点阐述所提方法。
1 动态运动基元及其泛化分析
1.1 动态运动基元
DMP模型是一个特征参数可学习的非线性吸引子系统,可以用于编码离散运动轨迹,DMP模型表达式如下:
(1)

(2)
(3)
其中,式(1)、式(2)本质上是一个弹簧阻尼系统,式(3)是一个正则系统(canonical system),这样设计是为了得到一个便于分析的稳定系统,并且可以通过调制非线性项达到期望的吸引子行为。式(1)~式(3)中,τ表示时间缩放量,用于调整运动轨迹的持续时间;y和z分别表示运动轨迹某时刻的位置和速度;y0和g分别表示运动轨迹的起始点和终止点;αz、βz是正常数,其关系通常设置为βz=αz/4。通过选择合适的值,可以使系统处于临界阻尼状态,从而使运动轨迹的终止位置y收敛到终止点g;αs是正则系统的常数;s是相位变量,用来替代时间变量t,使系统摆脱对时间的显式依赖,随着t的增加,s逐渐从1单调递减至0,由此可以保证系统最终收敛到终止点g;f(s)是系统中的非线性项,它是关于相位变量s的一个函数,可以通过调整不同时刻的吸引子行为来改变运动轨迹的形状。
为了实现更加通用的吸引子表达形式,定义如下:
(4)
φi(x)=exp(-hi(s-ci)2)
(5)
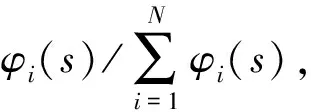
对于具有多个自由度的动态系统,需要对每个自由度分别单独建立变换系统,正则系统提供了各个自由度之间的时间耦合,而变换系统实现了每个自由度所需的吸引子动态特性。
1.2 动态运动基元泛化分析
在机器人示教学习领域中,泛化性能指的是当任务场景发生变化时,机器人仍能模仿示教运动的特征完成相应的任务。需要强调的是,单条示教运动轨迹学习所得的DMP模型也具有一定的泛化能力,其泛化能力在该运动轨迹任务参数附近具有较好的效果,但是当新的任务参数偏离该示教任务参数较远时,其泛化能力不能够令人满意。就整个机器人工作空间而言,如果只用单个任务参数处的示教运动轨迹的特征来代表整个工作空间的特征,显然是不合理的。因此需要在机器人工作空间采集多组示教运动轨迹,保证对应示教运动轨迹的任务参数尽可能均匀地覆盖整个机器人工作空间。对于一个新的任务场景下的任务参数,新的运动轨迹由多条示教运动轨迹生成。每条运动轨迹的形状特征由特征参数{ωi}(i=1,2,…,N)唯一确定,因此生成一条新的任务参数下运动轨迹可认为是生成一组新的特征参数。每一条示教运动轨迹对新的运动轨迹生成的影响是不同的,可以做出合理的假设:任务参数与新的任务参数越接近的示教运动轨迹对新的运动轨迹学习的贡献越大,新的运动轨迹的形状特征与同其任务参数相近的示教运动轨迹相似度更高。
2 动态运动基元泛化算法介绍
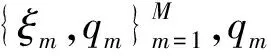
(6)

XW=f
(7)
(8)
(9)
其中,W和f分别为特征参数向量和非线性项向量,X为不同相位变量下的各个高斯基函数的值所构造的矩阵,特征参数W可以由式(7)对应的线性方程组的最小二乘解计算得到。
2.1 基于LWR的动态运动基元泛化
给定一个新的任务参数q,首先使用GPR(关于GPR的算法介绍参照2.2节)由q估计出运动轨迹终止点g和时间缩放量τ:
G(z):q[τ,g]
(10)
对于点到点的任务,一般将时间缩放量τ设置为常数,将任务参数q设置为运动轨迹目标位置g。
对于特征参数的泛化,使用局部加权回归,通过最小化目标函数V得到在新的任务参数下的特征参数W*:
(11)
可以认为,求出一组特征参数W*,使得新生成的运动轨迹与所有示教运动轨迹的差距最小,示教任务参数与q越接近的示教运动轨迹对特征参数W*的生成影响越大。式(11)中,Xk由式(9)计算得出,fk可由式(8)计算得出。任务参数空间中的K和距离d决定了每条示教运动轨迹对最终估计的控制策略的影响程度。K为核函数,文献[3]使用的是三次核函数,因为该核函数具有有限的范围和连续的一阶和二阶导数,并且在实验中表现效果较好,即
(12)
其中,d是任务参数q空间中的度量,由欧氏距离定义:
(13)
(14)
由式(13)和(14)可知,参数D完全由参数c⊂R唯一决定,通过最小化验证集误差来得到参数c。
2.2 基于GPR的动态运动基元泛化
对于每条示教轨迹,使用局部加权回归计算出对应的特征参数,对于每个ωi(i=1,2,…,N),通过最小化如下目标函数Ji:
Ji=(Sωi-f)TΓi(Sωi-f)
(15)
其中,f由式(8)计算得列;S为每个时刻t对应的相位变量值x(t)所构造的向量;Γi为ωi对应的高斯基函数在所有相位变量x(t)的值构造的对角矩阵。S和Γi定义如下:
(16)
由式(15)可以推导计算出对应的特征参数ωi(i=1,2,…,N)的公式:
(17)
对于M条示教运动轨迹,可由式(17)计算得到M组特征参数ωi(i=1,2,…,N)。
在一个新的任务场景下,使用GPR求出新的任务参数到该场景下的特征参数的映射。高斯过程(Gaussian process,GP)定义为
g(q)~GP(m(q),k(q,q′))
(18)

(19)
其中,W和W*为已知特征参数矩阵和待求特征参数;Q和q*为已知任务参数矩阵和新的任务参数;K(·,·)为相应的联合协方差矩阵,一种常用的协方差函数定义如下:
(20)
其中,σf、l和σn为常数,h(q,q′)定义为
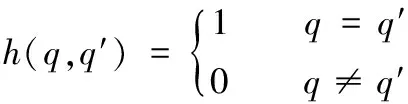
(21)
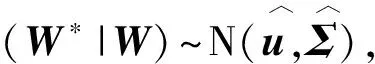
(22)
由式(22)可知,高斯过程回归与局部加权回归类似,与新的任务参数q*越接近的对应任务参数的示教运动轨迹对新的特征参数生成的影响越大。
2.3 基于任务参数加权的动态运动基元泛化
在实时运行的机器人模仿学习系统中,以上两种泛化方法存在运行速度较慢、在示教任务参数附近泛化性能较差等不足。本文提出了一种新的基于任务参数加权的动态运动基元泛化方法,相比以上两种动态运动基元泛化方法,在计算速度和示教任务参数邻近区域的泛化性能方面都有了较大的提高。
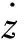
(23)
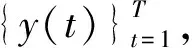
(24)
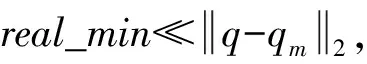
(25)
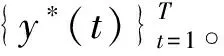
基于任务参数加权的动态运动基元泛化方法流程图如图1所示,流程如下:
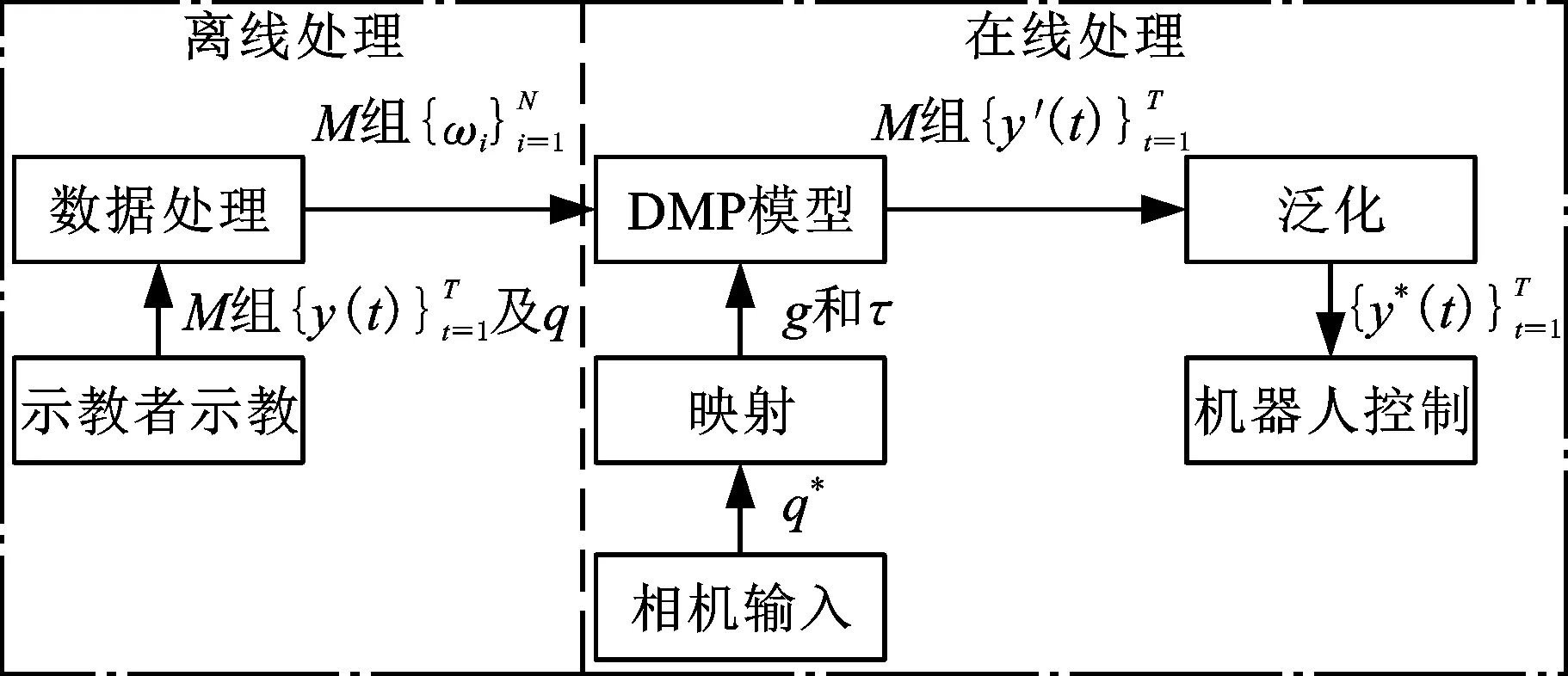
图1 方法流程图Fig.1 Flowchart of the method
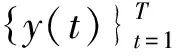
(3)相机输入。输入新的任务参数q*。
(4)映射。由式(10)计算q到g和τ的映射。
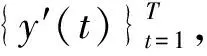
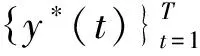
对于一个实时运行的机器人系统,步骤(1)、(2)可以进行离线处理,可以减少运行过程中的计算量,提高实时运行速度。
3 实验结果与分析
为了验证本文方法的有效性,设置了一个积木收纳的任务场景,如图2所示。实验中使用的机器人为Kukaiiwa协作机器人,视觉检测装备为Kinectv2深度相机,使用笔记本电脑作为上位机接收相机拍摄的任务场景信息,然后对机器人进行控制。该任务需要机器人将桌子上工作空间内摆放的积木收纳到积木桶中。首先,通过合适的示教方式获取示教数据,以示教数据为训练数据离线训练示教模型;对于一个新的任务场景,使用Kinectv2相机检测出积木颜色和形状特征以及位姿,获取任务参数,然后使用训练好的示教模型规划出运动轨迹;最后由PC机控制机器人按照指定运动轨迹完成任务,每次任务中机器人起始位置固定。

图2 积木收纳任务场景Fig.2 Building block storage task scene
3.1 数据采集与预处理

图3 动觉示教Fig.3 Kinesthetic teaching
机器人示教方法主要有三种:动觉示教、视觉示教及遥操作示教方法,三种方法各有优劣。本实验采用的是动觉示教方法,示教过程如图3所示。动觉示教也称作手把手示教,对示教者的技术要求较低,能够使示教者与机器人进行物理交互,感受机器人的运动模式及关节极限,由机器人自身的传感器记录关节角度和力矩的信息,为示教模型提供可靠的训练数据[5]。
示教区域与示教点布置如图4所示。示教区域的选择由机器人关节极限以及任务场景共同决定。对于示教轨迹数量M的选取,从理论上讲,有效示教轨迹数量M越多,模型的泛化性能越好,但总体来看,示教轨迹数量M并不是越多越好。首先,示教轨迹数量过多会导致模型计算效率下降,不利于运用在实时运行的机器人操作系统上;其次,示教轨迹数量过多会导致产生无效示教轨迹的概率增大,反而会对模型性能产生负面影响;最后,由于机器人示教学习方法倾向于使用小样本学习,在保证模型有较好性能的基础上,尽可能使用数量较少的样本,以减轻示教者的工作负担。示教轨迹数量M需要综合以上几个因素,根据具体的任务条件进行确定。本文共选取13个示教点,其中9个作为训练点,编号为1~9,对应的示教轨迹作为模型训练数据,为了使示教运动轨迹尽可能表示真实的工作空间特征,将9个示教点均匀布置在示教区域;另外4个示教点作为测试点,编号为a~d,对应的示教轨迹作为测试数据,用来检验泛化方法的泛化性能,不用于模型训练。
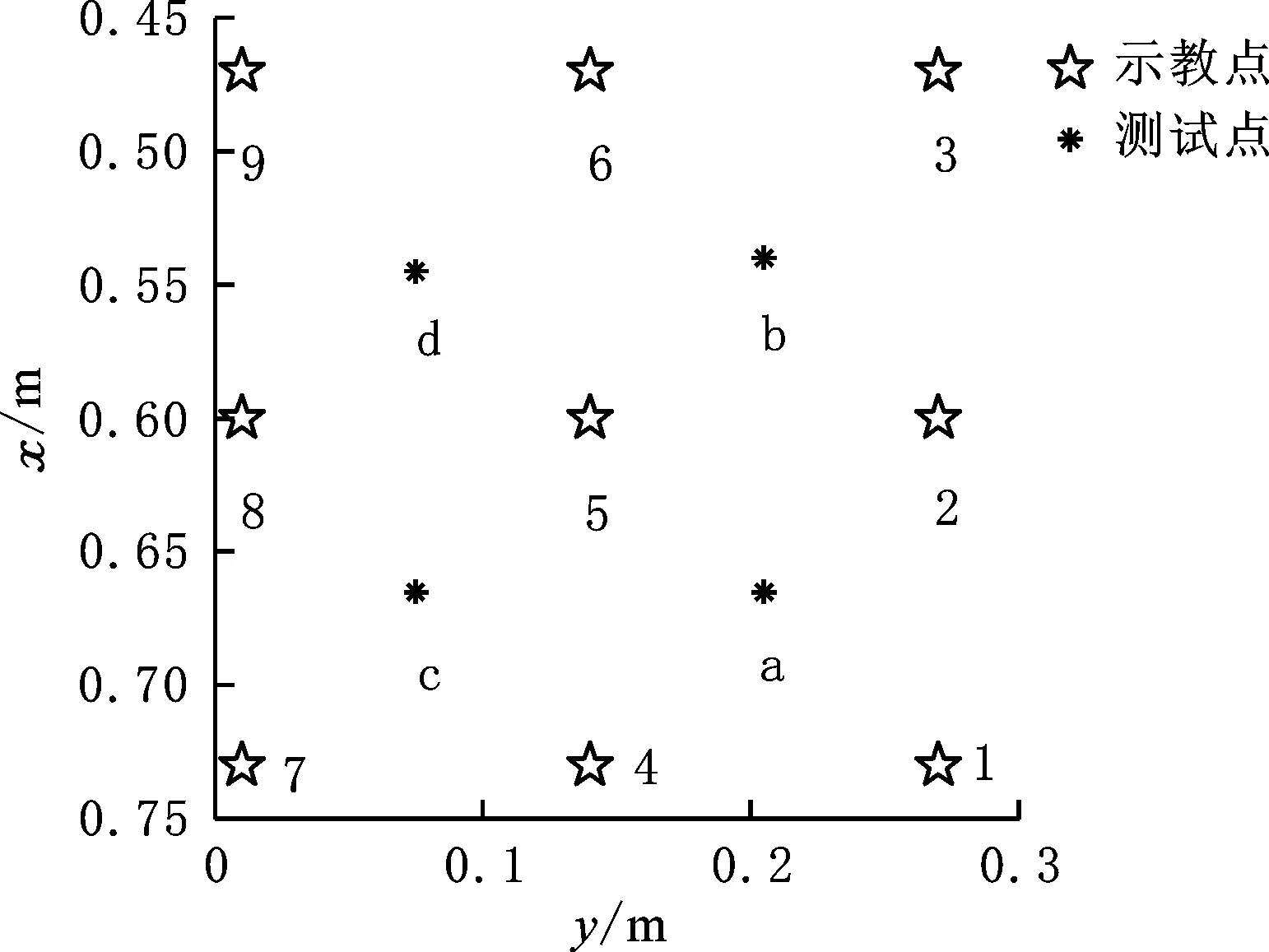
图4 示教区域与示教点布置Fig.4 Teaching area and teaching point arrangement
以示教点的积木空间位置作为任务参数,为了避免单条示教轨迹的随机性,在每个示教点以50 Hz的采样频率采集8组关节角轨迹,经过正向运动学将关节角轨迹转化为笛卡儿空间轨迹,对每个示教点的8组示教运动轨迹使用高斯混合模型(Guassian mixture model,GMM)建模,使用高斯混合回归(Guassianmixture regression,GMR)计算出均值作为该示教点的示教运动轨迹[6],如图5所示。
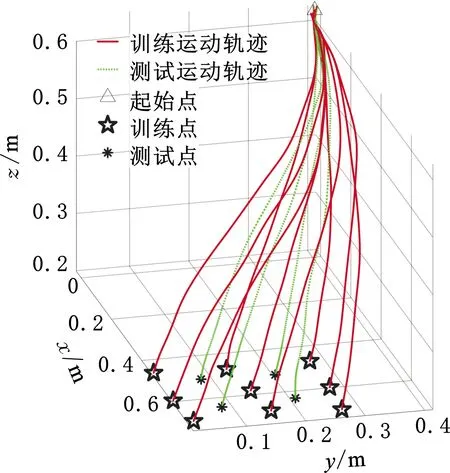
图5 示教运动轨迹Fig.5 Teaching trajectories
在使用三种泛化方法对训练数据进行建模的过程中,三种泛化方法的DMP部分超参数设置相同,基函数数量N=100,时间缩放量τ=1,αz=60,αx=1。
3.2 泛化性能分析
单次示教模型只包含单个示教点示教轨迹的特征,只在该示教点附近区域具有较好的泛化性能[7-8];多次示教模型则包含多个示教点示教轨迹的特征,可以使工作空间更大区域具有较好的泛化性能。为了比较单次与多次示教运动轨迹学习得到的DMP模型的泛化性能,以图5所示的4个测试点的积木空间位置作为待泛化任务参数,用两种模型分别生成相应的泛化运动轨迹,其结果如图6所示,多次示教模型泛化出的轨迹相比单次示教模型要更顺滑,变形更小,并且与图4的对应测试运动轨迹更加相似,可知多次示教模型泛化性能优于单次示教模型。相似度为
(26)
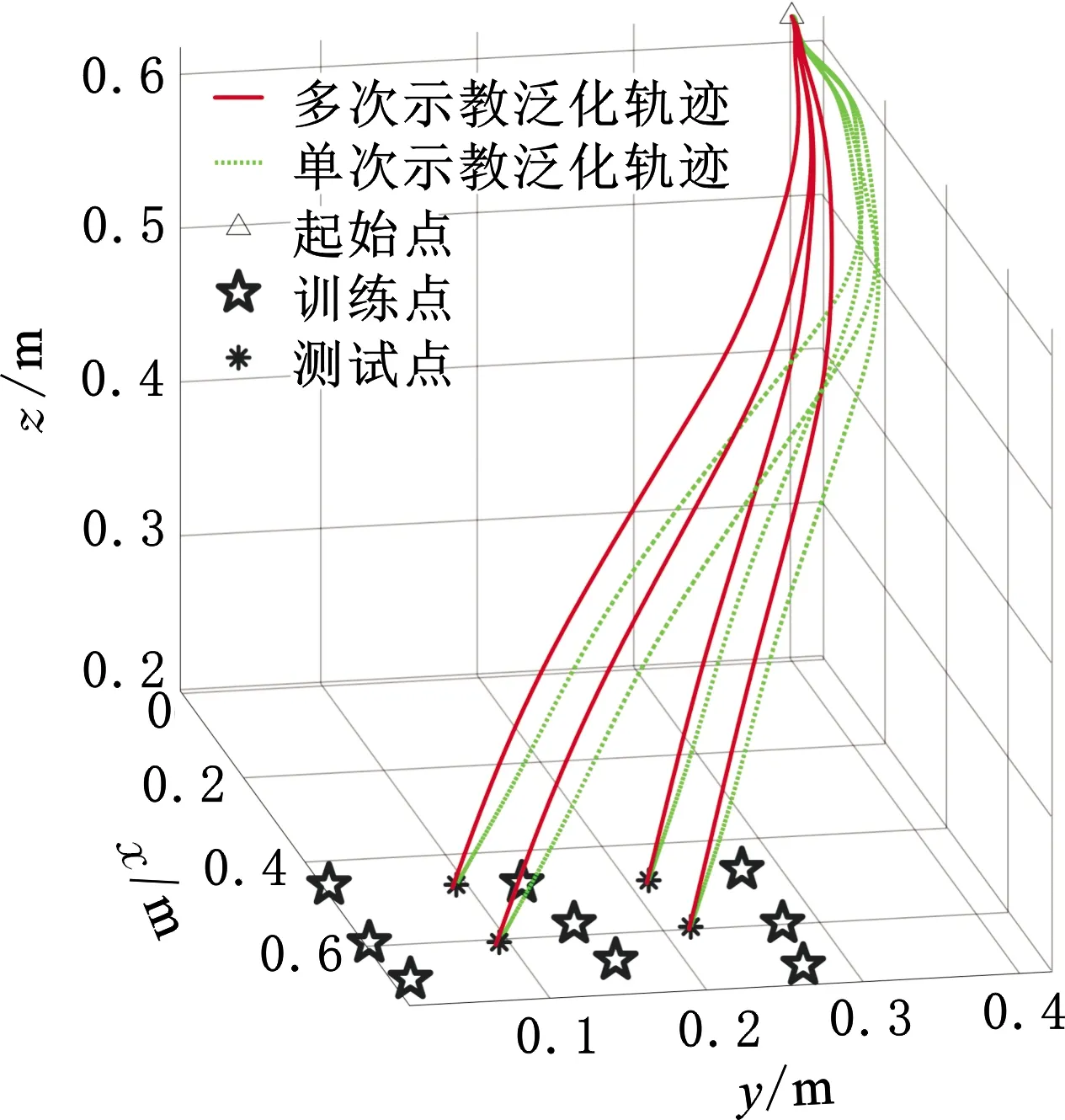
图6 单次与多次示教模型泛化性能比较Fig.6 Comparison of generalization performance between single and multiple teaching models
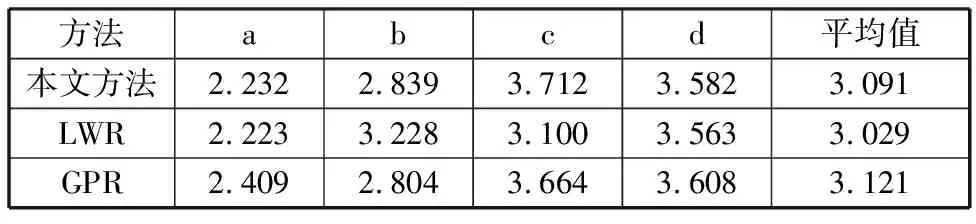
表1 远离示教点时泛化轨迹相似度比较Tab.1 Similarity comparison of generalized trajectories far from teaching point mm
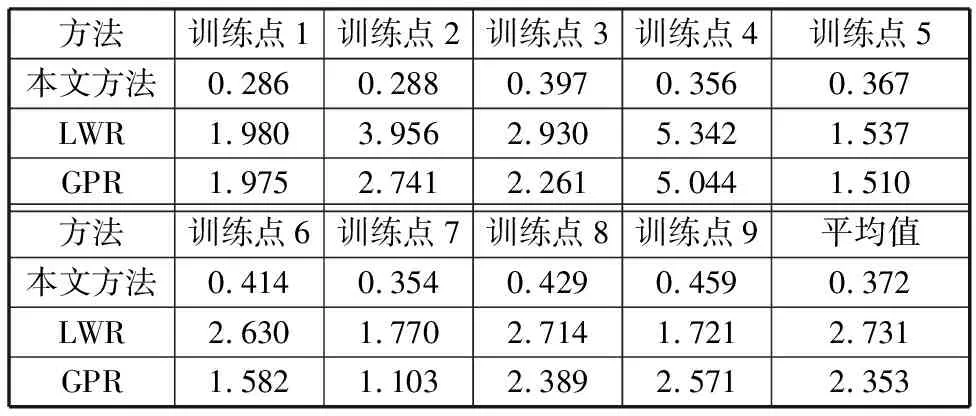
表2 示教点处泛化轨迹相似度比较Tab.2 Similarity comparison of generalized trajectories at teaching points mm
当任务参数远离示教任务参数时,由表1的4组数据可以看出,三种泛化方法与测试运动轨迹的相似度差别很小,加权方法对应4组数据的平均值与LWR方法的差别只有2%左右,而与GPR方法的差别不足1%,由此可以推断三种泛化方法在任务参数远离示教任务参数时泛化性能大致相同。当任务参数接近示教任务参数时,由表2的9组数据可以看出,在极限情况下,加权泛化方法与测试运动轨迹的相似度明显优于另外两种方法。
为了进一步分析三种泛化算法在示教任务参数附近的泛化性能,如图7a所示,对以第5个训练点为圆心、半径为20 mm的邻近区域进行分析。对于图中A、B、C、D四个方向,其中A、B分别与x轴和y轴平行,C、D为对角方向,以圆心为中心点,在每个方向均匀选取包括中心点在内的21个点作为泛化点,其中相邻两个点的距离为2 mm;对于每个方向的21个泛化点,分别用三种泛化算法生成相应的泛化运动轨迹,用式(26)计算出与示教运动轨迹的相似度,结果如图7 b~图7e所示。可以看出,在4个方向上加权泛化方法与示教运动轨迹的相似度都要优于另外两种方法。经过分析可知,本文方法在示教任务参数邻近区域的泛化性能好于另外两种方法。这主要是由于当示教轨迹数量M确定时,对比另三种方法,本文方法会给予离新的泛化点最近的示教点对应示教轨迹更大的权重。
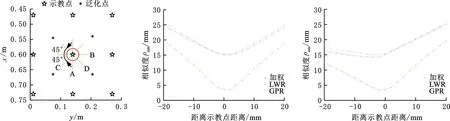
(a)示教任务参数邻近区域 (b)方向A (c)方向B
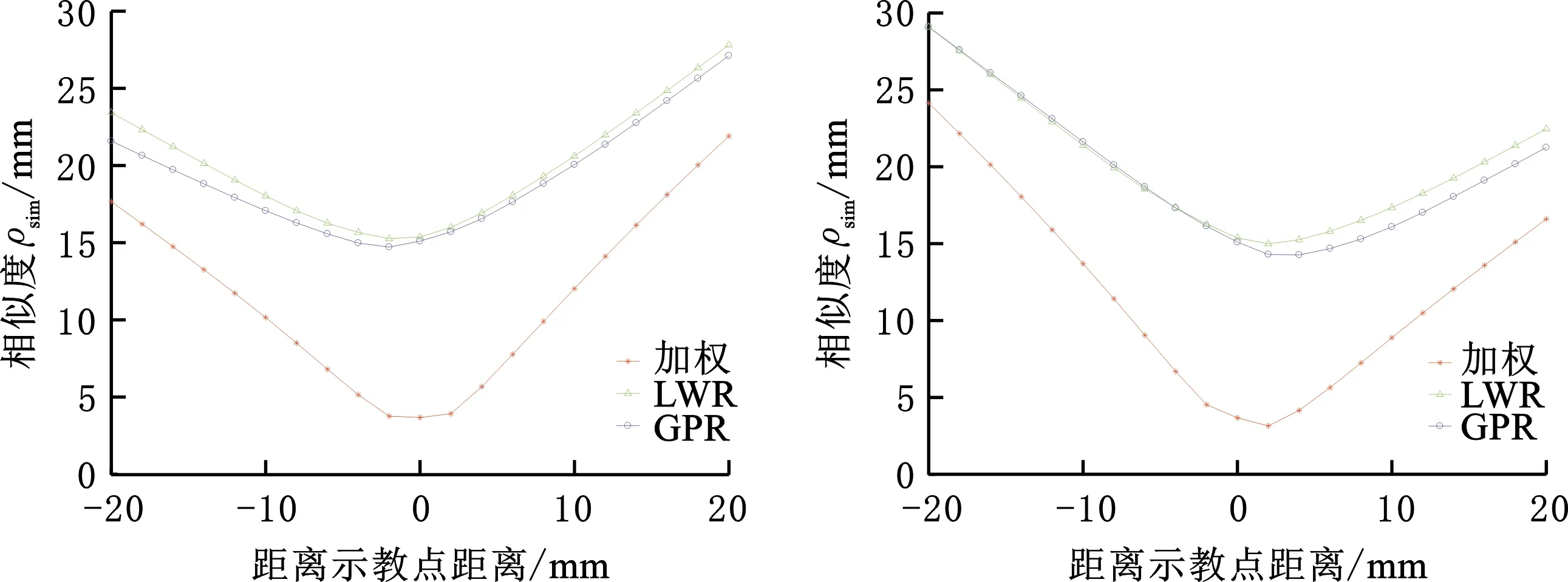
(d)方向C (e)方向D图7 示教任务参数附近泛化性能比较Fig.7 Performance comparison in the vicinity of teaching task parameters
3.3 计算效率分析
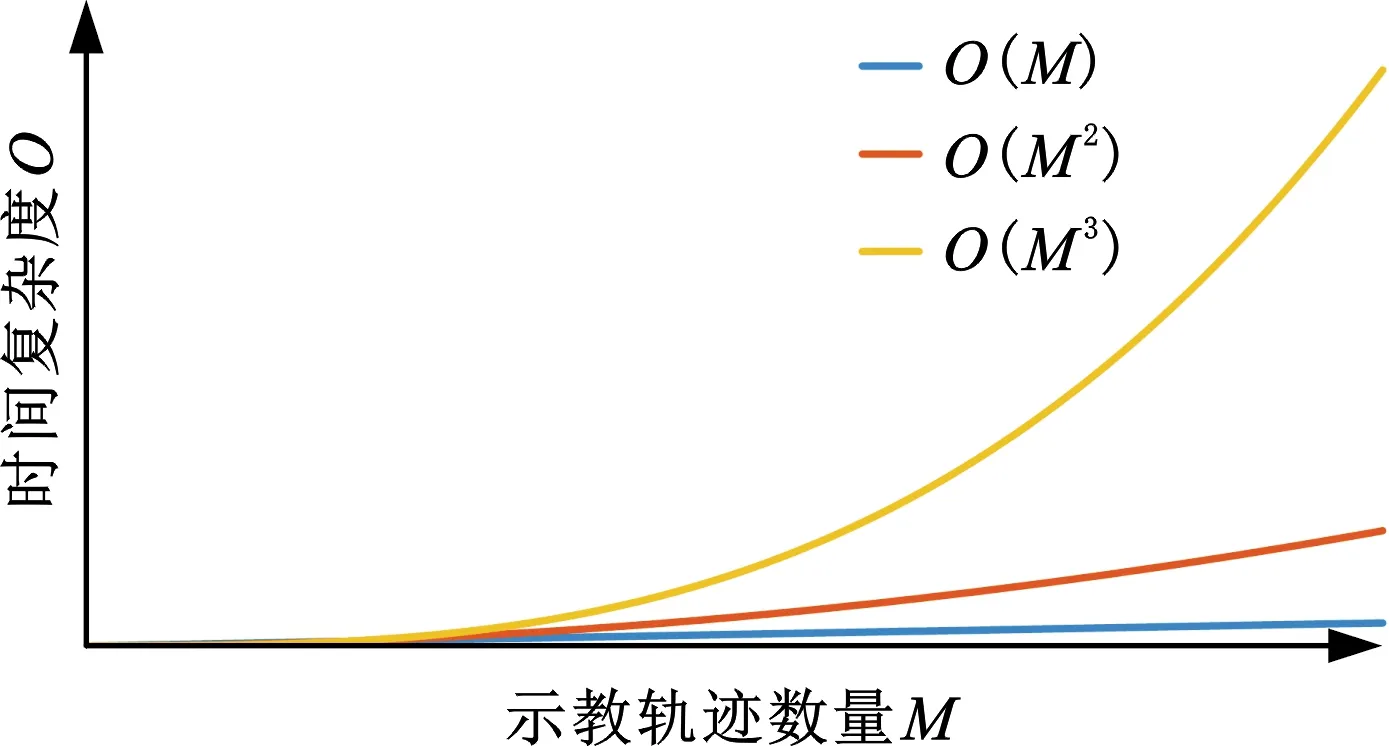
图8 时间复杂度增长趋势Fig.8 The growth trends of time complexity
就计算效率而言,主要考虑三种算法在线处理时的计算时间。从理论上分析三种方法的计算效率,相对于示教轨迹数量M,本文方法时间复杂度为O(M);基于GPR的泛化方法在求解式(22)时,需要对矩阵(K(Q,Q)+σn2I)求逆,时间复杂度为O(M3);基于LWR的泛化方法的计算时间集中在对式(11)目标函数的优化上,单次迭代时间复杂度为O(M2),总体迭代时间复杂度为O(lM2),其中,l为迭代次数。三种方法的计算时间都随着示教轨迹数量M的增加而增加,三种时间复杂度的增长趋势如图8所示,可以看出,本文方法的计算效率在理论上要优于另外两种方法。为了进一步比较三种方法在实验中的计算效率,对于图3所示的13个示教点,在使用三种泛化方法计算其泛化运动轨迹时记录了对应的计算时间,结果见表3。可见每种泛化算法在计算每条运动轨迹的时间大致相等,而且数值都在其平均值附近波动;加权和GPR泛化方法的计算时间远远小于LWR泛化方法的计算时间,这是因为LWR泛化方法在优化式(11)的目标函数时,迭代次数过多,平均约为432次,花费了大量计算时间;同时,加权泛化方法计算时间明显少于GPR泛化方法计算时间。分析可知,本文方法的计算效率相比另外两种泛化方法有了较大的提高。
3.4 积木收纳任务实验验证
为了验证所提方法的有效性,设置了积木收纳任务进行实验验证。在示教区域随意设置20个泛化点,如图9所示。在泛化点放置积木,以积木的空间位置作为待泛化任务参数,代入训练好的模型得到泛化运动轨迹,由PC控制机器人按照该运动轨迹完成积木收纳任务。单次积木收纳任务流程如图10所示,分别表示各种场景。共进行了20次积木收纳实验,其中成功了17次,成功率为85%,证明了本文方法的有效性。
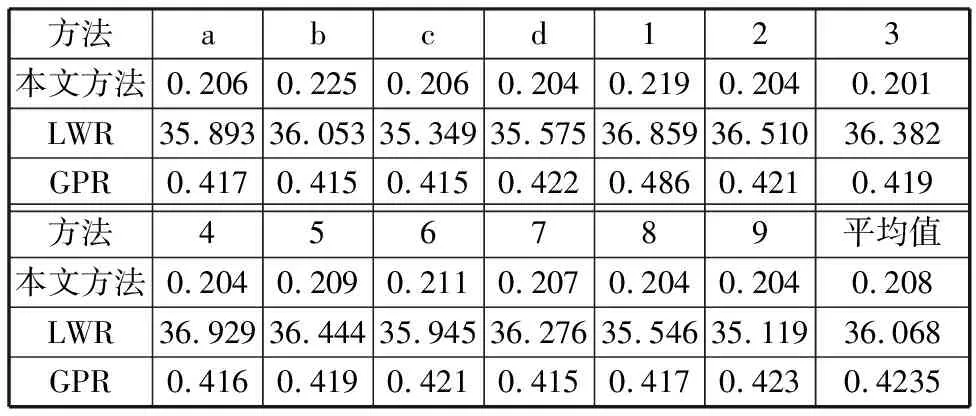
表3 计算时间比较Tab.3 Calculation time comparisons s
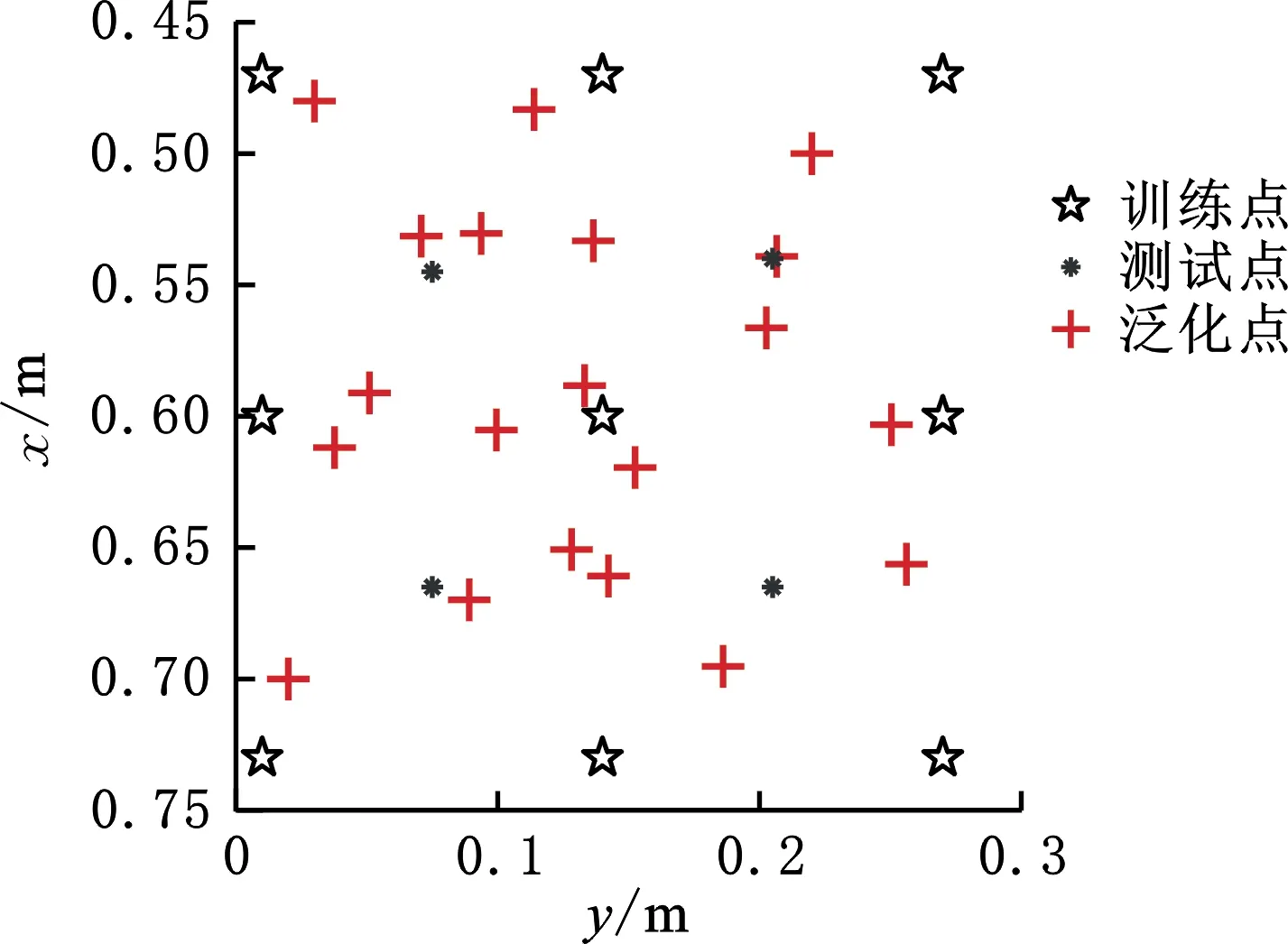
图9 积木收纳任务泛化点布置Fig.9 Layout of generalization points for building block storage task

(a)起始位置 (b)接近积木

(c)夹取积木 (d)靠近积木桶

(e)到达对应积木孔上方 (f)放置积木图10 积木收纳任务流程Fig.10 Process of building block storage task
4 结论与展望
针对机器人示教学习在新的任务场景下的泛化问题,本文提出了一种基于任务参数加权的动态运动基元泛化方法,与已有的基于LWR和基于GPR的泛化方法相比,在计算效率和示教任务参数附近的泛化性能方面有了明显的提升,使用Kukaiiwa协作机器人就积木收纳任务进行了机器人示教学习实验,证明了该方法的有效性。
本文方法主要针对的是机器人示教学习的轨迹层次的泛化问题,对于轨迹层次结合语义层次的泛化问题,该方法并不能很好地解决,这是目前机器人示教学习研究领域的一个难点和热点。一种可能的解决方法是将本文方法进行拓展,使用两种示教方式同时进行示教:一种采用拖动示教方式进行轨迹层次的泛化,另一种采用视觉示教方式进行语义层次的泛化,后续将继续开展所提方法的研究。

