基于RecurDyn的履带机器人雪地滑转性能

郭庆东，高兴华，刘晓飞，谢小宇，王开宝，李建永

(北华大学机械工程学院，吉林 吉林 132021)

按不同移动方式，在滑雪场作业的移动机器人主要有轮式、履带式、腿式以及复合结构式等几种[1-5].其中，轮式移动机器人对于复杂环境的运行适应能力弱；腿式移动机器人控制复杂；复合结构移动机器人机械结构复杂、控制难度较大；履带式移动机器人的系统控制简单、路况适应能力强[6-9]，已成为应用于雪场、林场、湖泊、沼泽等场所主要的移动机器人.J.Y Wong等[10]基于滑动摩擦理论对履带车在硬地面行走问题进行了深入研究；NT Aghdam等[11]基于Universal Mechanism(UM)软件仿真分析了履带式移动机器人在农业土壤、雪地、沙地等不同地形上的驾驶性能.以往的研究大多都假设履带在刚性地面上行走，而在雪地上行走的研究很少[12].

履带在雪地上行走具有众多优势[13]，如支承面积大，适合在雪地等松软地面行驶，并且履带下陷量小，滚动阻力小，通过性能较好；履带支承面上有履齿，牵引附着性能好，有利于发挥较大的牵引力；由于履带机器人的底盘较低，因此重心较低，在履带板的大面积支撑下，其行驶稳定性较好.但雪地下地面松软、含水量高、透水性低、抗剪强度低、压缩性强，机器人行驶会不可避免地产生滑转，严重时还可能会发生侧翻，导致行驶不稳定.因此，在雪地运行的稳定性成为履带移动机器人的重要指标，直接影响工作效率.本文以某雪地履带移动机器人为研究对象，进行运动学与动力学理论建模，仿真分析在不同密度雪地履带移动机器人的牵引力以及滑转情况，研究地面特性对运行性能的影响，为履带移动机器人在雪地行驶时的精确控制奠定理论基础.

1 地面滑转角分析

履带移动机器人模型见图1，主要由驱动轮、负重轮、诱导轮和张紧轮及履带组成.

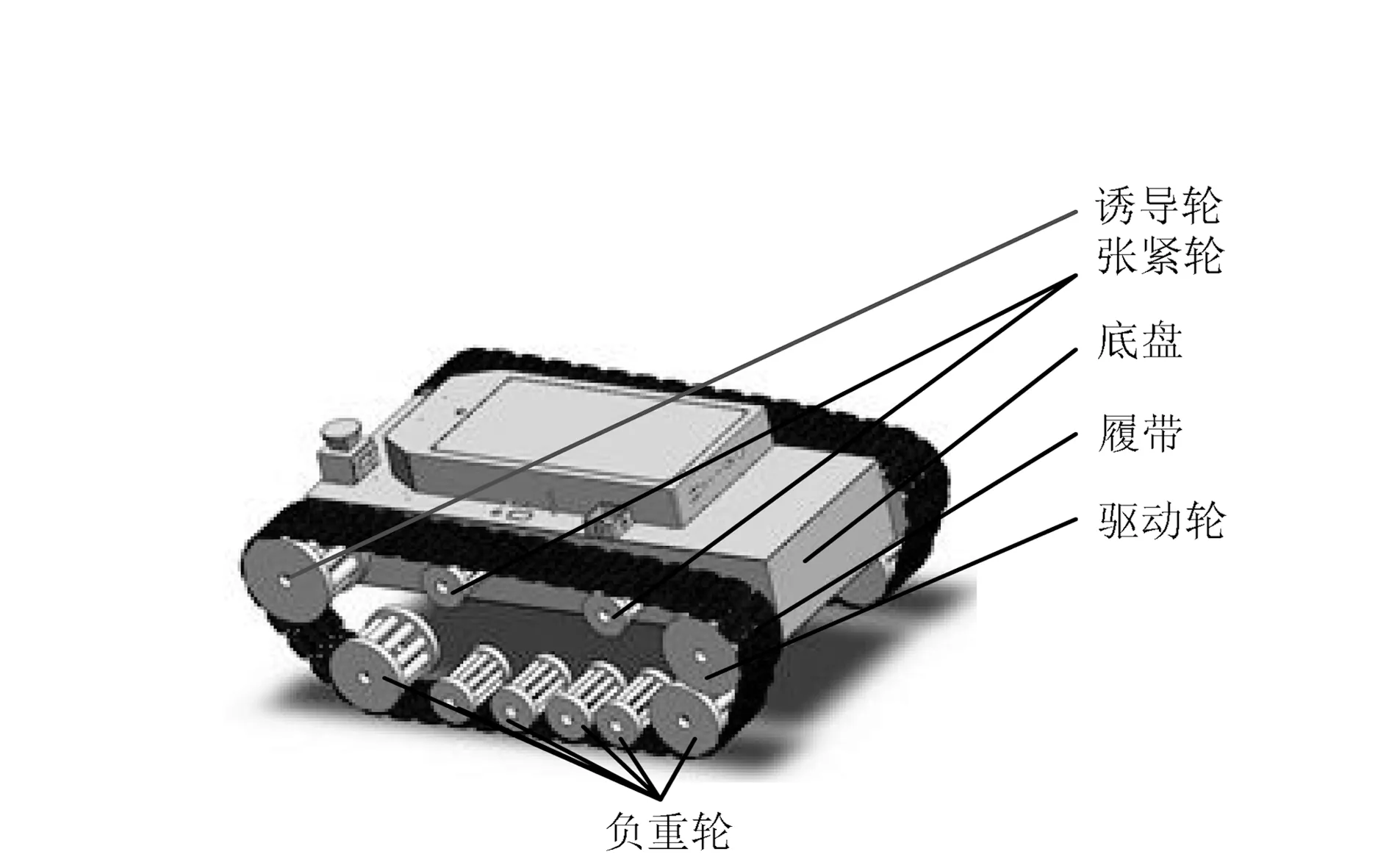
图1 履带移动机器人模型Fig.1 Model of tracked mobile robot

履带移动机器人做差分运动，通过驱动左、右两侧的驱动轮旋转带动履带运动.直线行驶时，两侧驱动轮转速保持一致，驱动履带机器人向前运动；转向时，由驱动轮带动诱导轮运动，内侧驱动轮减速，外侧驱动轮加速，此时两侧履带横向刮动地面，使地面对机器人产生一个较大的摩擦力，驱动履带转向.

与其他车辆的运动特性不同，履带车的受力更为复杂.在极限思想的基础上，采用瞬态运动分析法[3]建立履带移动机器人运动模型并进行简化.做以下假设：1)左、右两侧履带的接地长度、宽度完全相同；2)机器人仅在二维刚体平面上运动；3)履带和轮子之间高度联结，不存在位移，且忽略自身摩擦阻力；4)左、右两侧履带发生侧滑是一致的；5)履带所受的法向压力均匀分布.

建立履带车底盘在水平面行驶(包括滑转在内)的运动示意图，见图2.

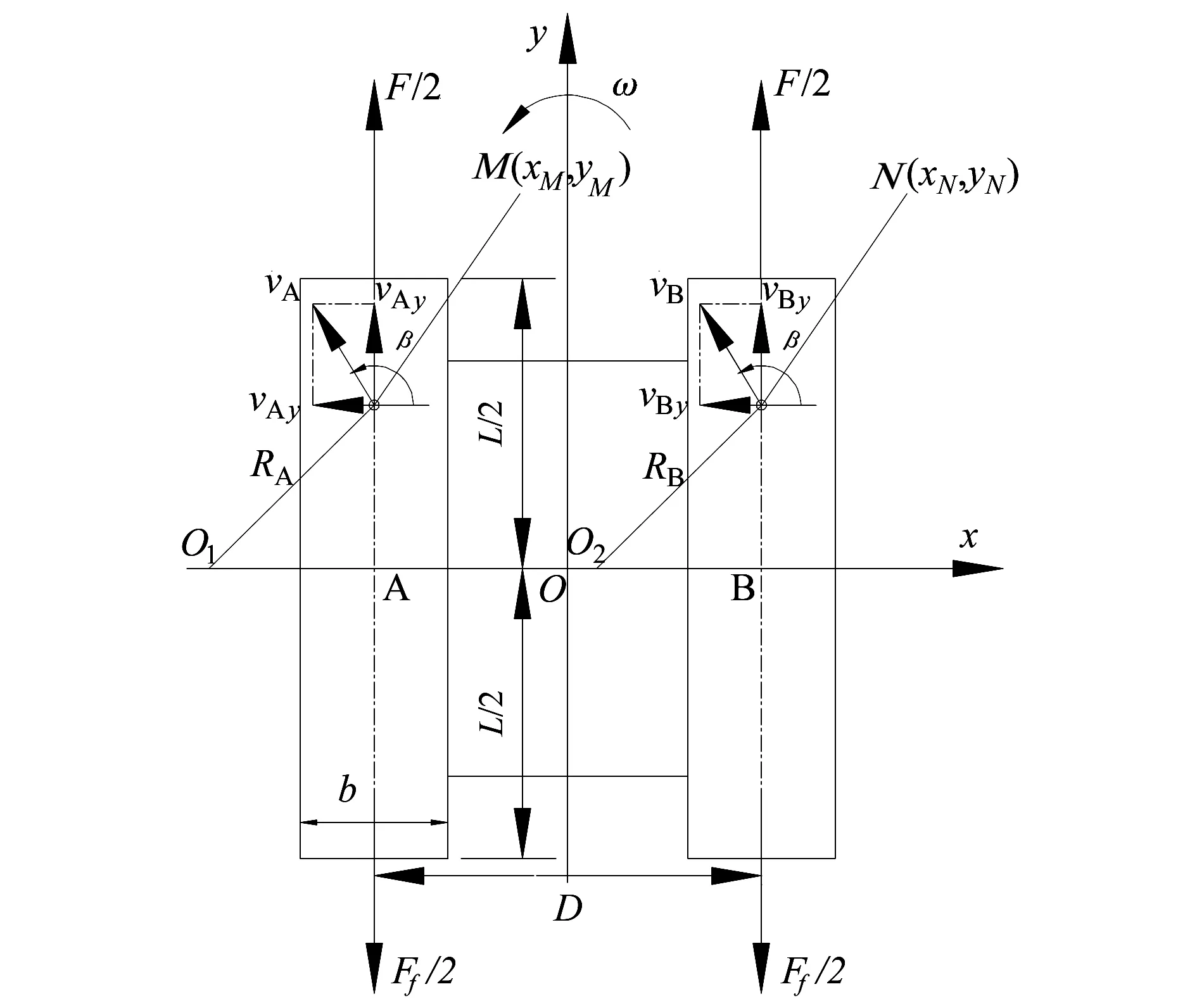
图2 履带运动平面Fig.2 Track motion plane

以履带车的几何中心为原点，建立xOy坐标系，x轴负半轴中的履带为A履带，正半轴中的履带为B履带.履带A中任意一点M的速度表示为vA，其坐标为(xM，yM)；履带B中任意一点N的速度表示为vB，其坐标为(xN，yN).将速度vΑ分解至x轴和y轴，分别得到vAx和vAy；将速度vB分解至x轴和y轴，分别得到vBx和vBy.

设在任意时刻履带滑转瞬时角速度为ω，履带A和履带B的滑转半径分别为RA、RB，则

在简化模型时，由于设定左、右两侧履带发生侧滑一致，因此，这里只研究履带A.将履带A的速度分解为vAx、vAy，RAx、RAy分别为x轴、y轴的滑转半径分量，得

在坐标轴x、y上的滑转位移分量

在M点的履带接地滑移角度

βM=arctan(vAy/vAx).

2 机器人运动模型

建立履带移动机器人在水平面行驶的受力示意图，见图3.

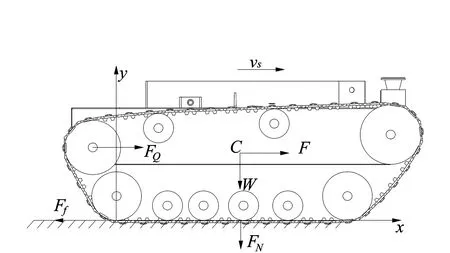
图3 履带车受力Fig.3 Stress of tracked vehicle

规定机器人质心为C，车体质量为m，单节履带宽为b，接地有效长度为L，两履带的轮间距为l，重量为W，牵引力为F，雪地产生的阻力为Ff，驱动力为FQ，所受压力为FN，履带行驶速度为vs.

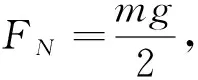
式中：nc为正弦波的周期；σ为法向压应力.

履带与地面发生相对滑动时，滑转率[14-15]

式中：i为滑转率；vl为履带理论速度.

单条履带在x轴上一点xj与地面之间的接触剪切位移

xk=i2xj，

式中：j=0，1，2，…；k=0，1，2….

由剪切应力-位移关系公式得

τx=(c+σtanφ)(1-exk/K)，

式中：τx为剪切应力；c为内聚力；φ为内摩擦角；K为剪切变形模量.

单条履带剪切地面产生的驱动力

在移动过程中，履带移动机器人所受阻力

Ff=Ff1+Ff2，

式中：Ff1为履带滚动阻力；Ff2为履带压实地面产生的阻力.履带滚动阻力

Ff1=fmg，

式中：f为滚动摩擦因数；履带压实地面产生的阻力[16-17]

式中：kc为土壤内聚变形模量；kφ为土壤变形的内摩擦模量；n为沉陷指数.

综上可得履带移动机器人单履带牵引力

3 仿真分析

3.1 履带移动机器人动力学

利用多体系统动力学仿真软件RecurDyn建立履带车底盘模型，并简化为履带行走机构和车身部分.行走机构包括履带、驱动轮、负重轮、导向轮、张紧轮、支撑杆和张紧弹簧.在模型中添加约束条件，将车本体上的控制系统及开关等外设部件去除，只在计算车体质量及转动惯量时加入参数，输入履带模型参数，建立履带模型.履带模型参数见表1.

表1 履带移动机器人模型参数Tab.1 Model parameters of tracked mobile robot

冰雪特性直接影响履带移动机器人的运动性能.雪从自由降落到形成压实冰雪会经历积雪、压雪、冻结压雪等过程，其密度与特性参数均不相同.冰雪地面的机械特性参数见表2[18-20].

表2 冰雪地面机械特性参数Tab.2 Mechanical characteristic parameters of ice and snow ground

由于不同密度雪地特性参数不同，使得具有相同接地压力的履带在面对不同密度雪地下的运动特性不同.履带与不同密度雪的特性参数见表3[18-20].

表3 履带与不同密度雪地面特性参数Tab.3 Characteristic parameters of crawler and ice and snow ground with different densities

通过建立动力学模型，并在RecurDyn中建立不同密度雪地，得出履带移动机器人在不同密度雪地下行驶的速度、加速度，见图4和图5.由图4和图5可知，在运行5 s内，由于雪地密度不同，导致达到稳定运行速度的响应时间不同.在积雪地面上，履带移动机器人受到积雪地面的阻力大，响应时间长，在加速度趋于0 m/s2时，其速度未达到设定速度，存在稳态误差；在压雪地面上，受到的阻力比积雪地面小，响应时间短，且稳态误差较小；在冻结压雪地面上，受到的阻力小，并且出现打滑现象，在加速度趋于0 m/s2的过程中发生大幅震荡，导致车体运行不稳定.

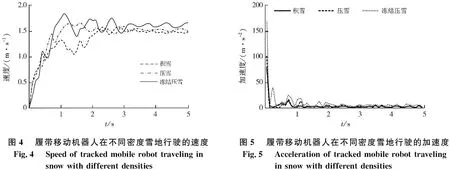
图4履带移动机器人在不同密度雪地行驶的速度Fig.4Speed of tracked mobile robot traveling in snow with different densities 图5履带移动机器人在不同密度雪地行驶的加速度Fig.5Acceleration of tracked mobile robot traveling in snow with different densities

3.2 不同冰雪地面滑转率

计算滑转率时，假设驱动轮能产生足够大的牵引力，履带会使雪地产生形变，根据地面力学公式计算出履带移动机器人的受力情况，然后反映到数学模型中.

根据运动学方程，得出在不同密度雪地机器人的滑转率.设置恒定速度为1.5 m/s，仿真分析在3种不同密度雪地行驶时的牵引力、滑转角，见图6和图7，牵引力与滑转率的关系见图8.

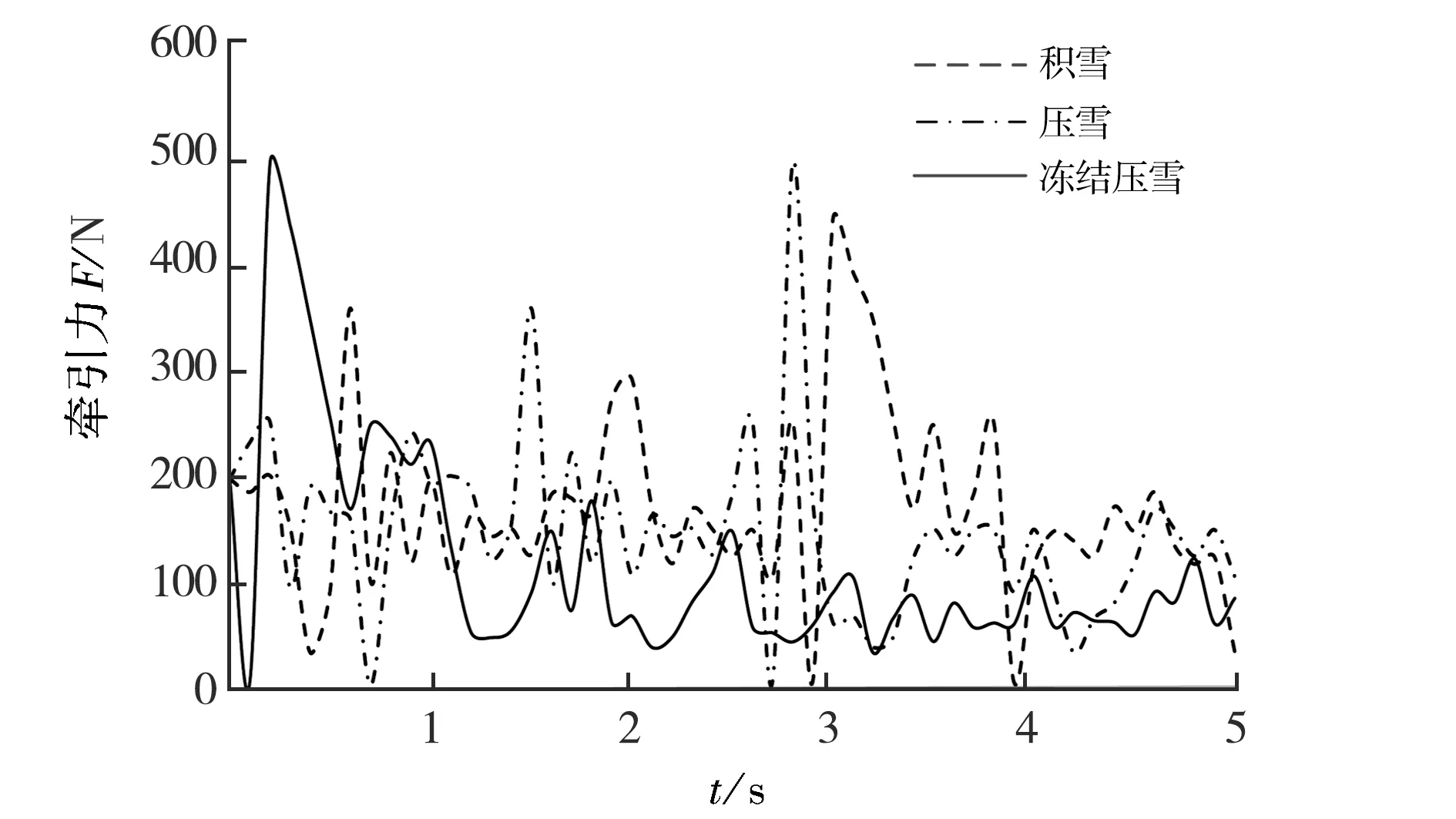
图6 履带移动机器人在不同密度雪地行驶的牵引力Fig.6 Traction of tracked mobile robot driving in snow with different densities

图7履带移动机器人在不同密度雪地行驶的滑转角Fig.7Slip angle of tracked mobile robot driving in snow with different densities图8履带移动机器人在不同密度雪地行驶的牵引力、滑转率Fig.8Traction and slip rate of tracked mobile robot driving in snow with different densities

根据仿真结果可知：在行驶过程中，履带移动机器人达到匀速的牵引力为200 N.在积雪地面的滑转角变化相对较小，压雪地面次之，冻结压雪地面变化较大；滑转率和滑转角与雪密度紧密相关，履带移动机器人行驶时，牵引力需克服雪地阻力，在相同密度雪地，滑转率与牵引力正相关，滑转率随牵引力的增大而增大.不同密度雪地滑转率差异较大，在相同驱动力矩下，积雪密度越大滑转率越大，发生滑转和侧翻最为严重；滑转率对车辆轨迹的影响不可忽略.

综上，积雪地面雪密度较低，积雪与黏土混合，其黏性增加，致使履带车运行阻力增加，到达目标速度的时间较长；压雪地面雪密度增加，其黏性降低，运行阻力减小，运行响应时间缩短；冻结压雪地面雪密度进一步增加，履带车移动阻力减小，但滑转率增大，易发生滑转与侧翻.

4 小 结

通过建立履带移动机器人数学模型，利用多体动力仿真软件RecurDyn对履带底盘进行三维建模，仿真分析在积雪、压雪、冻结压雪3种不同密度雪地的行驶情况，分别获取履带移动机器人的速度、加速度、牵引力、滑转角以及滑转率曲线.结果可知：

1)在压雪地面下运行平稳；在积雪地面，由于阻力较大，运行响应时间较长；在冻结压雪地面加速过程中，由于地面阻力较小，会发生震荡现象.

2)履带移动机器人在积雪地面行驶阻力较大，所需牵引力较大，并且滑转角随着牵引力增大而增大.

3)在相同牵引力下，雪密度越大，滑转率越大；雪密度越低，运行越稳定.在相同雪密度下，牵引力越小，运行越稳定.