基于逆向思维的初中物理解题指导
李小勤

【摘要】物理本身的知识兼有抽象、复杂等特性,相应题型复杂多变,综合性强,对初中生思维能力、解题能力等具有较高要求,为了从根本上助力初中生解题能力提升,就需要抛弃“题海战术”的方式,侧重解题思维、方法与思想等的传授及指导.本文针对初中物理解题教学现状,对逆向思维在解题中的运用意义与要点进行了重点探讨.
【关键词】初中物理;逆向思维;解题方法
在學科核心素养下,“真学”、“真教”方面的话题越发受到关注.所谓的“真教”是指以培养初中生学科核心素养为根本出发点,基于大单元理念等有效教学方法对教学的内容进行创新整合,以及实施多元化的新型教学方法与手段,保证可以全面促进学生学科综合素质发展.其中逆向思维是一种相对正向思维或顺向思维而言的有效思维方式,在某些复杂或者无法借助正向思维进行求解的物理问题求解中常常可以发挥奇效.
1 逆向思维的内涵
逆向思维也被称作求异思维,主要是指反过来思考那些已经近乎成定论的观点或事物的一种思维方式,也就是所谓的“反其道而行”.
逆向思维本身是相对于正向思维而言的一种求异思维方式,侧重从对立面来发展思维,或者从问题反方面来进行探索,力求可以借助这种打破常规思维的思维方式来获得全新的的结论或看法.
在分析问题中,正向思维下的思维是先得出条件或问题,后得出结论.而在逆向思维下,可以从结论反过来推导问题或条件.针对某些正向思考之后无法获取解题思路的问题求解,如果可以灵活运用逆向思维,那么有时候常常可以突破常规,简化问题的整个求解过程.
2 初中物理解题中逆向思维的运用价值
物理是初中阶段一门非常重要的学科,对学生的逻辑、抽象以及逆向等多样化思维发展以及解题能力具有较高要求.为了有效锻炼初中生的物理解题能力,离不开切实可行的解题训练,但是以往侧重“题海战术”的解题训练方式会使学生在反复解题的过程中形成思维定势,尤其是在反复求解同类型的物理问题过程中更是容易限制思维能力发展,直接影响了学生最终的解题能力的发展.而如果可以在解题教学中有计划地传授给学生逆向思维这一解题手段,那么可以指导他们反过来从结果推导验证问题的条件,以此就可以便捷地对问题求解过程进行简化.
初中生本身的阅历尚浅,年龄比较小,同时逻辑思维、抽象思维等思维能力发展不足,以至于在分析物理问题的过程中常常无法开展深入思考,进而直接影响了最终的物理问题求解能力的发展.而此时如果可以结合一些典型的物理问题,针对性将逆向思维法传授给学生,让他们可以在尝试利用逆向思维来求解物理问题的过程中持续性锻炼及发展自身的解题能力.
3 初中物理解题中逆向思维的运用策略
3.1 基于逆向思维,解决运动问题
运动学问题是初中阶段物理学习中比较常见的一类问题,相关问题求解中也经常可以借助逆向思维来进行求解.由于初中生本身初步学习物理学科知识,学习的时长相对较大,物理思维发展还处于初级阶段,所以在碰到某些已经学习过的物理知识的时候常常会因为印象不深而无法形成深刻认知,以至于常常无法顺利求解问题.
特别是在运动学问题设计过程中,出题人会对有关的条件进行改变,这时候学生因为处于无法深入理解及掌握物体运动状态,所以无从下手.而此时如果可以指导初中生在对运动学问题进行剖析过程中巧用逆向思维,从末端物体运动状态往回进行推导,逐步还原到最初的“原态”,以此就可以帮助他们对物体运动特征及规律等进行有效梳理,明确最终的运动状态本质,保证可以借此来助力他们快速找到解题突破口.
例1现有一辆装满支援灾区救济货物的货运车,已知其载满货物之后的总重量是35000N.在装满货物之后,货运车以10m/s速度在水平路面上允许行驶,在行驶10min之后,已知行驶中货车所受阻力是3000N,试求该辆货运车在10min之内牵引力对货运车的作用是?货运车的功率是?
解析 本道物理题是一道典型的关于运动的问题,如果初中生采取常规思维方式进行思考与探究,那么就容易受到货运车总载重35000N这一已知条件的干扰而造成错解问题.
实际上,在求解本道运动学问题的过程中不需要运用到这一已知条件,为了可以帮助初中生意识到这一点,可以指导他们采取逆向思维来进行思考,即:首先可以采取位移(距离)计算公式S-v×t来进行计算.在10min时间之内,货车行驶的距离达到了10s×10m/s×60=6000m.在货运车保持匀速行驶的状态下,可以有效地调用“力的作用是相互的”这一基本物理定理来快速推导得到:货运车本身所承受牵引力和阻力之间保持对等关系,即:F=f=3000N,相应的货运车发动机牵引力对货运车作用是W=F×s=6000m×3000N=1.8×107J,对应的功率是P=W/t=30000W=3×104W.
在求解本道物理运动学问题期间,通过指导学生采取逆向思维思考问题求解过程,可以帮助他们规避问题求解中存在的干扰条件及信息,同时可以从所求结论逆向推导已知的条件,确保可以顺利确定货运车发动机牵引力、阻力以及功率三者之间所具有的紧密联系.通过指导初中生反复开展解题训练,可以有效地提高他们分析及求解问题的效率.
3.2 基于逆向思维,解决磁场问题
在现实生活中,初中生比较熟悉的是能够借助肉眼直观观察到的事物,如汽车的运动或者水的浮力,但是也存在着一些现实生活中肉眼无法直观观察或用手触摸的事物,磁场、电场等都是该类的物理知识.
针对磁场问题,由于初中生本身无法直观感受它们的存在,所以在分析及求解中容易陷入解题困境.这时候如果可以巧用逆向思维,则可以从磁场问题已经给定的各种解题条件出发来进行逐步推导,并且在推导过程中可以时刻思考“求解问题需要哪些必要的解题条件与数据?”“如何才能获得这些解题条件与数据?”这两个方面的问题,保证他们可以对相应物理问题求解过程进行简化,不断提高学生解题的准确性.
例2图1所示的是一个匀强磁场中搁置有一个忽略电阻的平行金属导轨,已知大线圈m和导轨之间保持连接状态,并且在导轨上面相应地搁置一根裸体导线ab,为了可以使大线圈m上的闭合线圈形成顺时针的感应电流,那么这时候需要如何移动导线ab呢?
解析 本道题是一道非常常见的磁场问题,主要考查学生对磁场中电流形成机理的掌握情况,以及磁场方向与电流方向辨识能力发展情况.按照正向的解题思维,初中生在思考的过程中常常会运用“右手法则”,根据导线移动来判断所产生磁感电流的方向.但是在分析本道物理问题过程中如果可以采用逆向思维,借助逆用“右手法则”的方式就可以快速判断出导线ab的移动方向(向右).
本道题虽然简单,但是,确是运用逆向思维求解磁场问题的一个具体表现,对促进他们自身解题能力与逻辑思维能力有积极意义.
3.3 基于逆向思维,解决浮力问题
浮力问题也是一类中考物理考试的必考题型,本身涉及到的题型灵活多变,可以帮助初中生快速求解相关的物理类型题,单纯依靠正向思维是远远不够的.因为浮力方面的物理计算公式比较多,并且根据解题指标的不同将相应的物理计算公式进行相应地变形,为了可以更好地帮助他们求解浮力问题,同样可以指导初中生采取逆向思维来逆用相应的浮力计算公式.
通常而言,在浮力作用下,假定物体本身不发生改变,那么在同一个g下浮力大小也不会发生改变.在求解相关物理问题过程中如果可以紧抓这一物理知识点与规律来运用逆向思维分析问题,那么就可以帮助他们在反向思考问题求解方向与流程的过程中判断出最终的正确结果.
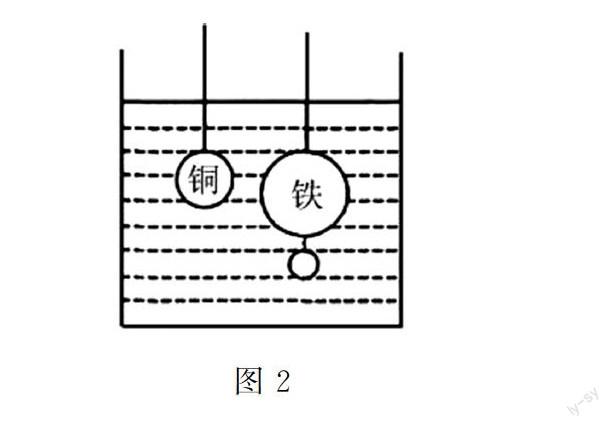
例3 图2展示的是一个盛有清水的水杯中搁入一个铜制实心小球和铁质实心小球,它们分别借助一根可以忽略体积与质量的细线进行连接并悬挂在同种类型的弹簧测力计下面.在两个实心金属球完全沉入水杯中的清水时发现两个弹簧测力计的示数相同,那么在将它们提出水杯中的清水面之后,哪一个弹簧测力计的示数更大一些?
解析 本道浮力题涉及到比较繁琐的实验描述过程,虽然整体描述比较清晰,但是大多数初中生一般都不习惯对拿出的2个金属小球之后的质量进行测定,所以分析起来难度比较大.
如果在指导他们求解问题过程中可以灵活运用逆向思维,对题干给出的物理实验来设计如下一个相反的实验:假如现有两个金属小球在提出清水面之后的重量保持一致,那么结合浮力计算公式:F浮=ρ液×g×V排发现大体积的铁球本身承受的浮力要更大,为了可以保证提出水面之后弹簧测力计测得的示数保持相等,那么这时候就需要给铁球相应地多悬挂一些事物,这样就可以借助逆向思维的运用来顺利求解问题.如果2个弹簧测力计显示相同示数,那么在提出小球之后悬挂有铁球的测力计会具有更大的示数.
在指导学生灵活应用逆向思维对问题进行反复简化的过程中,可以拓展他们的解题思维,提高他们解题效率.
例4 现有一个空的玻璃瓶子,将其进行密封处理之后插入到盛有清水的水盆中,发现该瓶子正好悬浮于盆中清水当中,试求该玻璃瓶子体积与瓶中空气体积二者之比?(已知玻璃密度是2.5×103kg/m3).
解析 针对本道浮力问题求解,许多初中生在求解的过程中会联想到采用正向思维来分析及求解问题,即:他们通过发现玻璃瓶子懸浮于盆中清水当中,所以可以假定这时候玻璃瓶子密度和水的密度均是1,也就是说玻璃瓶子本身缺少容积部分质量之后,剩余的同玻璃瓶子之内空气这一整体密度可以近似看作是1.此时假定总体积是V1,容积是V2,玻璃和水的密度分别是ρ1和ρ2,这样就可以得到如下解题公式:ρ1V1-ρ2V1=ρ1V2,代入已知条件之后可以相应地通过求解来得到如下比值:2.5∶2.除了这种正向求解思维外,如果可以指导学生采取逆向思维来求解问题,那么就可以根据本道题所要求解的体积比,逆向思考运用密度公式来进行解题,之后即可调用二力平衡方面的知识来进行列式求解问题(具体步骤同上述的正向思维方法一样).
相较于正向思维而言,如果可以灵活地应用逆向思维,那么就可以从问题出发来反推解题条件,这样可以快速简化问题求解过程,保证快速确定解题的突破口与思路.
4 结语
综上所述,逆向思维是助力初中生高效求解物理问题的一个有效思维方法,具体可以将其应用于解决运动问题,电磁问题、电学问题和浮力问题等不同类型的物理问题中.
在指导学生利用逆向思维解决物理类型题中,必须要加强逆向思维运用的有效指导,保证他们可以借助逆向思维来简化整个问题求解过程,最终快速求解问题,有效锻炼及发展他们的物理解题能力.

