在地形图描画中培养学生数感
姚怀宇


[摘 要]帮助学生积累数学活动经验,培养学生的应用意识和创新意识是数学课程的重要目标,综合与实践活动是实现这些目标的最佳途径。在综合与实践活动中,教师不宜过早地对素材进行数学化抽象处理,而应该强化数学学习方法,归纳数学公式和定理,积极引导学生进行观察、分析、反思,使综合与实践活动优质高效。
[关键词]综合与实践;海南岛;描画;数学化;观察
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2022)14-0049-03
综合实践活动作为新课程标准明确规定的主要内容之一,理应扎实推进。新课程标准明确指出,开展综合实践活动,就是要以问题为载体,让学生怀着好奇心和探究欲自主参与实践活动。它是教师通过问题引导来贯穿一个相对完整的活动过程,让学生在体验式学习中领悟知识。那么,该怎么贯彻新课程标准,有效开展数学综合实践活动呢?在一次区级巡回讲堂展示课中,笔者有幸观摩了一位特级教师上的“描绘海南岛的地形图”一课,现将其课堂实录摘要整理,并做一些简单的点评,以期与同行探讨。
一、导出问题,激发探索需求
师(课件展示海南岛风光图片,包含海口市、三亚市、三沙市、儋州市等地):请从未去过海南岛的同学举手。
师:刚才你们是不是被海南岛的迷人风光给吸引了?老师曾随团游览过海南岛,旅行前还特意买了一本旅游攻略《海南岛游历指南》,它对海南岛做了详细的描述。(课件出示资料:海南岛本岛南北长283千米,东西长257千米,海岸线长约1080千米。)看了这段文字描述,你们有什么想问的?
生1:海南岛的地理区划面积有多大?
生2:海南岛的地形地貌像什么几何形状?
生3:海南岛的常住人口有多少人?
师:你们的问题提得很好。刚才有同学问海南岛的地形地貌像什么几何形状,仅靠上述三个数据,能概括海南岛的几何形状吗?
生4:能。海南岛南北长283千米,东西长257千米,所以看起来像一方手帕。
师:它不是标准的方形,因为标准的方形长和宽都是一样长的。你还有什么想说的?
生4:它更像一个长方形。
师:以上三个数据不足以说明问题吗?怎么处理才能揭示其形状?这是首先跃进老师脑海的一个式子——(283+257)×2=1080,对于这个式子你有何感想?
生5:这个式子与长方形的周长公式相吻合。
师:的确。都是先求出长加宽的和,然后再乘以2。据此推测,海南岛的地形地貌接近什么几何形状?
生6:长方形。
师:计算时,我们不妨对各项数据做近似处理,如将283看作300,把257看作250,這样估算所得的数据1110比海南岛的实际海岸线长度(1080)要——
生7:长。
师:对!海南岛的海岸线长度其实就相当于这个类似的长方形的周长。
师:现在你可以说说海南岛的几何形状了吗?
生8:海南岛不是一个标准的长方形。
师:它不是一个规则的长方形,它的边线是蜿蜒曲折的,不是平直的。
许多学生从未去过海南岛,对于其地形地貌更是一无所知。教师选择海南岛最具代表性的风景图和数据,引导学生提出“海南岛的地理区划面积有多大?”“海南岛的地形地貌像什么形状?”“海南岛的常住人口有多少人?”等问题,从而激活了学生的探究欲。学生根据自己的生活经验说出“海南岛像一方手帕”“海南岛不是标准的长方形”等,教师再通过数学算式启发学生列式来深度揭示海南岛的几何形状。学生通过列式、观察,发现海南岛的海岸线长度与长方形的周长相吻合。
过去我们常认为,综合与实践活动属于科学劳动课,一定要让学生亲自动手实践,或者实地考察,绝不能纸上谈兵。有人曾认为综合实践活动是变相的文化补习,是披着综合实践“外衣”的课堂教学。其实不然,像本节课,引导学生认识海南岛的地形图就是一种有效的综合实践活动。世界之大,包罗万象,宇宙乾坤,无穷无尽,我们不可能什么地方都亲自踏足,不可能什么学问都亲身体验,有时通过图片和模型也能达到同样的目的,甚至效果更好。比如研究海南岛的地形地貌,亲自游览海南岛不见得比观看其地形图来得清楚。学生通过观察海南岛的地形图,能从海岸线的轮廓中抽象出一个标准的几何图形,然后利用所学的周长计算公式近似计算出其海岸线总长。但是,要让学生明白这种处理所得的数据不能完全取代真实值,海南岛真实的海岸线长度要比这个计算结果大。
二、画海南岛,实现数形结合
1.一画海南岛,初成雏形
师:如果要你描绘出海南岛的地形,你打算怎么画?
生1:先画一个长方形。
师:这个长方形的尺寸如何设计?老师这里有“4厘米×1.5厘米和8厘米×3厘米”两种尺寸,你选择哪一种?
师:请各小组交流讨论,拿出一个方案。
(学生交流讨论)
师(出示图1):这是第一组设计的作品。
生2:这个形状太随意了。
师:还有其他意见吗?
生3:数据不对,宽为257千米,不应该是250千米。
师(出示图2):这是第二组设计的作品。哪位同学先来点评?
生4:感觉边线弯折后比原长更短了。
师:为何变短了?请用已学的知识做出合理的解释。
生5:因为缩进去的斜边比两条直角边的长度总和要短。
师:缩进去的也不是平直的线段,谁还有更好的解释?
生6:海南岛的实际周长要比长方形的周长长,而长方形的内接“椭圆”的周长比长方形周长短,所以不对。
师:为什么内凹的线条一定比这两条线段之和要短些?
生7:我是将内凹的线条看成近似的直线,它和长方形两边组成一个近似的直角三角形,而根据三角形边长特征“两条直角边的长度和要长于斜边的长度”,于是“椭圆”的周长小于长方形的周长。(掌声响起)
师:这次我们又用到了什么知识?
生8:三角形的两边之和大于第三边(直角三角形两直角边之和大于斜边)。
师(出示图3):这是第三组设计的作品。对于这组作品,你们有何想法?
生9:它过于狭长。
师:先说优点。你看作品的轮廓符合长方形的形状,但是海岸线的褶皱太多,总长度势必会超过长方形。同学们,通過刚才的研究,我们知道要在长方形的基础上描绘出海南岛的地形,不能一蹴而就。在描画的时候,需要注意哪些细节?
生10:南北、东西线不能超出长方形的长和宽。
生11:表示海南岛海岸线的弧线不宜太多,也不宜太少,要适量。
2.二画海南岛,“画”出数感
师:现在请再画一次海南岛的地形图。
(学生尝试画图,与同桌交流后集中反馈)
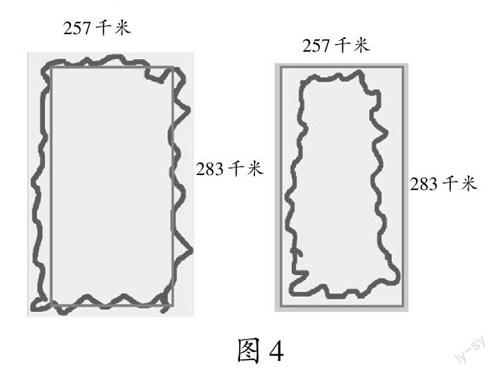
师(出示图4):这是第四组设计的作品。前后对比,你发现了什么?
生12:有改进!
师:对。失败的作品可为后面成功的作品提供借鉴和参考。刚才有同学问海南岛的土地面积有多大(课件出示:海南岛的土地面积约为3.6万平方千米),看到这个数据,你有何感想?
师:资料里提供的海南岛的土地面积是3.6万平方千米,而有同学测算出的却是7.5万平方千米[300×250=75 000(平方千米)],为何会有这么大的差距?
生13:因为海南岛的海岸线是弯弯曲曲的,所以其面积比长方形的面积要小得多。
师:海南岛的实际土地面积占长方形面积的几分之几?
生14 :大约二分之一。
生15 :五分之三。
既然是从综合实践活动中探寻数学理论知识,就会存在一个不可回避的问题,那就是操作中总会出现这样或那样的误差,因为实际与理论总不会那么吻合,比如海南岛的轮廓,虽然学生尽力使其往长方形无限逼近,但因为海岸线的无规则弯曲,所以不可避免地存在误差,但是误差是宝贵的教学资源,它也给教学带来了新的契机。学生判断误差是偏大还是偏小后再调整调整,学习新的理论和新的知识。如图2,将内凹的曲线看成三角形第三边,它比两条直角边的和小,是利用了“三角形两边之和大于第三边”这条推论。由此可见,即使是在无法精确算出数据的情况下,也能通过定性分析得出相对可靠的结论,而且在整个去伪存真的过程中印证的各种定理,也是一次数学知识大“串烧”。
三、课后分析
教师课前为学生呈现了一个直观形象的学具——4厘米长、1.5厘米宽的长方形,让学生据此勾画海南岛的地形图,整个过程精彩纷呈。
一是放手让学生自主探究,教师进行评议。每一次画海南岛,教师总是先提供一些引导性信息,促进学生数学化思考,并重点展示学生的作品,让学生说说想法,然后集中交流评析。学生毫无保留地说出自己的创作经过和真实体验,并对他人的作品提出中肯的评价和建设性的意见。绘图者虚心聆听意见,认真反思,虚心接受,不断修正、改良,使自己所勾画的图形越来越接近海南岛的真实地貌,教师则一直从旁指点。整个过程,师生配合默契,互动良好。
二是画图的要求呈现梯度爬坡,提供必要数据,实现数形结合。二画海南岛以后,教师呈现了海南岛的面积数据,并提问“看到这个数据,你有何感想?”当学生算出海南岛的土地面积为300×250=75 000(平方千米)时,教师让学生进行对比,引发学生对计算值和真实值存在巨大差距的认知冲突。在学生思维发展的高潮期,教师总是能趁热打铁,使学生的思维水平得到提高。
本次活动前后两次画海南岛,第一次画海南岛是着眼于周长,而且反复画了几幅作品,每幅作品都有不足之处,但是出示的作品一幅比一幅有进步,这是因为每次尝试都是有目标的,每次尝试都是带着科学严谨的理论,所以操作误差在不断缩小,无限向精确值靠近。第二画次海南岛也是这样,在真实面积和估算面积之间不断寻找平衡,不断寻找造成误差的原因,然后在允许误差存在的情况下,计算出真实面积占估算面积的几分之几,让学生从误差中跳脱出来,切换到分数计算的知识领域,这就是综合实践的魅力:可以在各个环节串联起不同的知识,并通过看似随意的知识串接,培养学生的数感。
三是学生通过反思和修订,使得所画图形越来越接近海南岛的真实形貌。在每一次学生完成绘图任务后,教师都会善意地督促学生反思。如一画海南岛后,教师提出:“为什么内凹线条一定比这两条线段之和短些?”在教师的质疑下,学生自我反思,唤醒旧知,积极求证,最终检索到了“三角形任意两边之和大于第三边”的理论依据。又如二画海南岛后,教师运用对比,引导学生“失败的作品可为成功的作品提供借鉴和参考,前后对比一下,你会有更多的发现。”,提醒学生思考哪些地方考虑欠妥。一个个环环相扣的问题,促使学生发现自己的不足,并不断反思和寻求理论依据,然后加以修正完善,对海南岛的形貌由最初的模糊抽象到后来的明确具体,数感在画图的过程中逐渐明晰,学生的数学活动经验不断丰富,数学综合实践活动的基本特色得以充分彰显。
[ 参 考 文 献 ]
[1] 刘莉.“综合与实践”教学助力学生发展:小学数学“综合与实践”学与教的案例研究[J].小学数学教师,2021(9):31-35,2.
[2] 张东萍.课内外结合开展小学数学教学,让“数学好玩”[J].求知导刊,2021(36):20-21.
[3] 韩涛,王勇.在“综合与实践”活动教学中渗透数学文化[J].数学教学通讯,2021(19):29-30.
[4] 王夏莲.小学高年级数学综合实践课堂教学效率之我见[J].天津教育,2021(19):74-75.
(责编 黄春香)

