通过辨析比较策略有效利用错误资源
薛风清
在数学学习过程中,学生经常会出现各种各样的错误。作为教师,要善于探寻学生发生错误的原因,采取适当的策略,有效利用错误资源,让错误成为促进学生学习、提升教学效率的有效资源。加强辨析比较是有效利用错误资源常用的一种策略。以下结合笔者的教学经验,谈谈如何通过辨析比较的方法纠正错误,促进学生有效学习。
一、在学生“概念不清”时运用辨析比较
在数学学习过程中,有些概念学生记住了,但没有理解知识本身的内涵,在应用时常常出错。这时,教师应站在学生的角度思考问题,了解学生发生錯误的原因,帮助学生清除问题背后的障碍,使学生真正理解知识、掌握知识。
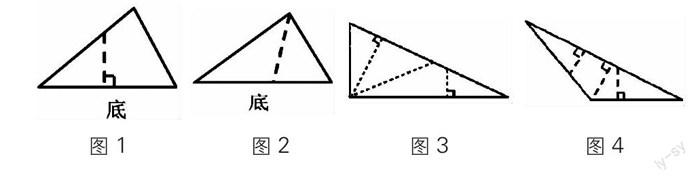
例如,引导学生认识三角形的高是人教版四下“三角形的特性”一课中的重要内容,当学生在学习了三角形的底和高的概念后,教师结合课件演示三角形底边上的高的画法,帮助学生借助图形理解知识。在此基础上,让学生独立进行画高练习(完成教材第60页做一做),学生画三角形的高时,主要存在以下几个问题:(1)不是从三角形的顶点向对边引垂线,而是从一条边上的任一点向邻边引垂线(如图1);(2)画高不规范,画的时候凭感觉,虽然是从顶点出发,但画出的高不垂直于底边(如图2);(3)由于直角三角形两条直角边互为底和高,当碰到要画直角三角形直角边上的高时,有的学生无从下手,有的学生则从直角的顶点向斜边斜着画。教师在巡视过程中,发现以上错误资源后并不急于指出,而是在三角形中画出一些线段,让学生辨析哪些是高,哪些不是高,并让学生说说为什么?(如图3、4)通过对图3、图4的正误判断、对比辨析,帮助学生认清三角形高的本质。使学生明白了这个知识点的三个核心要素:从顶点引出;必须向对边,而不是向邻边引出;必须是垂线段。在此基础上,让学生判断自己画的高是否正确,并说明理由。大部分学生自己发现了练习中存在的问题,自觉进行纠正。
二、在学生“概念混淆”时加强辨析比较
有些数学概念,在形式上比较相近,学生容易被知识的表象迷惑,形成概念混淆,并出现错误。遇到这种情况,教师应把握概念的本质,巧妙引导学生进行对比,准确地揭示易混淆概念之间的联系与区别,让学生在比较中区分概念、理解本质。
例如,人教版四下的“乘法结合律”和“乘法分配律”就是学生容易混淆的两条运算定律。单纯学习乘法结合律时,学生掌握得较好,但在学习乘法分配律后,有的学生在运算过程中把乘法结合律和乘法分配律混淆了,在使用中错误百出。在一节练习课中教师出示算式15×(60×6),学生在练习过程中主要出现了以下两种错误的计算方法:(1)15×(60×6)=(15×60)×(15×6)=900×90=81000;(2)15×(60×6)=(15×60)+(15×6)=900+90=990。显然,这是混淆了乘法结合律和乘法分配律。针对这一错误资源,笔者首先引导学生从概念的形式上进行对比,再通过复习乘法分配律的字母表述:(a+b)×c=a×c+b×c,使学生可以清楚地看到,只有当两个数的和(或差)乘以一个数时,才能使用乘法分配律。题目中的算式15×(60×6)是三个数连乘,只能用乘法的结合律或交换律来简便计算。在形式和意义的对比之后,教师设计练习题,让学生在正误比较中明晰概念。
例题:判断正误(对的画“√”,错的画“×”)。
(1)125×(80+8)=125×80+125。( )
(2)125×(80+8)=(125×80)×(125×8)。( )
(3)125×(80+8)=(125×80)+(125×8)。( )
(4)125×(80+8)=125×80×8。( )
教师通过预设例题,引导学生辨明容易混淆的“错点”,让学生在有限的时间里,通过独立做题辨别、分析、探讨,对乘法运算定律的本质有了更清晰的认识,让原先出错的学生找到错因,纠正错误。这样,学生不仅可以知道错误的原因,而且知道如何纠正错误。也可以帮助学生加深印象,真正地理解算理。
三、在学生“经验不足”时进行辨析比较
小学生年龄小,生活经验尚浅。有些数学概念,对于他们来说比较抽象,即便学过,认识也不够清晰。甚至有些时候,还会因生活经验的“负迁移”,影响了学生对数学概念的正确理解,导致在知识运用的过程中发生错误。
例如,笔者在教学人教版二下“克与千克”的相关内容时,发现学生对重量单位的理解在一定程度上受生活化语言的影响,从而发生错误。在教学过程中,笔者出示一道与量感有关的题目:“一个正常成年男人的体重约( )千克。”全班50多位学生只有不到50%的学生所填写的数据合理,还有超过50%的学生填写的数据严重偏大或偏小。数据严重偏小的学生对“千克”这个计量单位缺乏正确的认识,而数据严重偏大的学生则是受生活经验及生活化语言的影响。如:学生的父亲体重为160斤,他就直接填写160千克。针对这种错误资源,教师应把生活中的“斤”与数学学科中的“千克”“克”进行比较,让学生明白数学中的1千克等于生活中的2斤,1斤等于500克。通过对错误资源的分析,沟通生活中的“斤”与数学中的“千克”的区别与联系,从而发现错误、纠正错误。另外,教师在平时的教学中也可以设法避免负面影响,借助学生在生活中积累的经验更好地帮助他们理解数学中的数量关系,正确使用计量单位。
四、在学生“似是而非”时引导辨析比较
在练习过程中,有些题目相似度比较高,乍一看,不容易发现内在区别,容易导致出错。这时,教师要引导学生从多角度、多方位进行辨析比较,找出它们的细微区别,让学生充分说理,使他们在交流、倾听中理解算理,掌握方法,从而达到深度学习的目的。
例如,笔者在教学人教版三上“多位数乘一位数”的相关内容时,出示练习题:24×5○25×4(填上“>”“<”或“=”),大部分学生不假思索地填了“=”。在评讲过程中,笔者让各种答案的学生分别发言,说说自己的想法。填写“=”的学生说道:“算式中的‘2一直都在十位,个位上的‘4和‘5交换了位置,答案不变。”部分学生对这种观点表示赞同,但也有一些学生立即提出反对意见,他们的表述主要如下:(1)两个算式中个位上的4和5交换位置,表示的意思就变了,24×5表示的是5个24的和,25×4表示的是4个25的和,这两个结果不相等;(2)24只比25小1,但5个比4个多一个二十几,所以不相等;(3)个位上都是4乘5得20,但左边算式的十位是20×5=100,右边是20×4=80,所以24×5>25×4;(4)25×4=100,20×5=100,24×5一定比100大,所以24×5>25×4。教师引导学生通过不同角度说理、辨析,验证24×5=25×4的填法是错误的,并提出正确的填法,使原来想法错误的学生在倾听中深刻理解了错误的原因。
(作者单位:福建师范大学第二附属小学 责任编辑:宋晓颖)
——辨析“凌乱、混乱、胡乱、忙乱”

