画图策略在数学教学中的运用

陈燕

[摘 要]画图策略与几何直观联系紧密，可以有效链接形象思维和抽象思维，在二者之间形成一条连接逻辑空间的纽带，让学生在探究和理解数学知识时不断提升几何直观能力。在小学数学教学中，教师要根据具体的教学内容和学生的实际情况灵活运用画图策略，使之成为学生理解概念内涵、诠释算理本质、拓展解题思路、创新思维方法、助力经验积累的重要武器，于无形中渗透数形结合这一数学思想方法，提高学生的数学学习效率。

[关键词]画图策略;数学教学;运用

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2022）21-0008-03

著名数学家华罗庚曾说过：“数形结合百般好，割裂分家万事休。”“数”与“形”反映了事物两个方面的属性。数形结合，指数与形之间的一一对应关系。数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”（即抽象思维与形象思维的结合），将复杂问题简单化、抽象问题具体化，从而实现优化解题思路的目的。因此，在数学教学中，教师应根据具体的教学内容和学生的实际学情，适时渗透数形结合这一数学思想方法，引导学生巧妙运用画图策略解决问题。这样既可以丰富学生的解题思路，提高学生解决问题的能力，又能提升课堂教学效率和学生的数学核心素养，使学生在数学学习上得到更好的发展。

一、画图策略揭示概念内涵

小学生的思维正处于由形象思维向抽象思维过渡的时期，所以抽象的数学概念令他们感觉晦涩难懂，进而影响对所学数学知识的理解。因此，教师要想深刻地揭示数学概念的本质，仅靠单纯的口头讲授往往收效甚微，而借助数形结合的直观性，可以深化学生对数学概念的理解。

例如，教学人教版数学教材第七册《倍的认识》这一内容时，“倍”本身就是一个比较抽象的概念，所以学生解题时经常因为错误理解而出错，即使教师反复纠正，学生也不知道自己错在哪里。面对这样抽象的数学概念，仅靠教師的口头讲授，很难让学生理解。因此，笔者教学时另辟蹊径，借助几何直观，先出示两组图（见图1），让学生观察对比，再分析两种图形的数量关系。这样，学生就能直接观察得出：椭圆形和三角形的数量之间存在倍数关系，即把2个三角形视为一份（虚线打圈），那么6个椭圆形就有这样的三份（三个虚线圈）。在学生初步感知“倍”的外在形式后，笔者让他们圈一圈，将“倍”的外在形式用分堆计数的方法表示出来，从而巧妙地转化成数学上“倍”的概念。在学生掌握“倍”的概念后，笔者仍借助三角形和椭圆形，随机举出若干倍数的例子，让学生尝试在作业本上画出示意图。这样反复通过几何直观，先后揭示和展示倍数，巩固和加深了学生对“倍”的概念的理解。

由此可见，教学数学概念时，教师如能借助几何直观，从“数”和“形”两个维度诠释数学概念，让学生进行切实有效的体验感知，建立正确的概念表象，就能深化学生对所学数学概念的理解和掌握。

二、画图策略诠释算理本质

要想提高学生的计算能力，就要让学生理解算理，因为理解算理是理论支撑和方法保障。但是，算理不像算法那样具体可感，因为算理是抽象的，甚至没有准确的科学语言来定义，只能靠学生去领悟。如果学生没有深刻理解算理，或者根本无视算理的存在，甚至把算理当成儿戏，每次都是重复例题的演算步骤，就极易形成僵化思维和机械行为，导致解决问题时束手束脚，计算时呆板、生硬。那么，如何让学生理解算理呢？画图是一条捷径。图形能够直观反映计算过程的细节，并演绎出每一步计算的逻辑原理，其推理过程都记录在图形中，这些优势能协助学生理解算理。

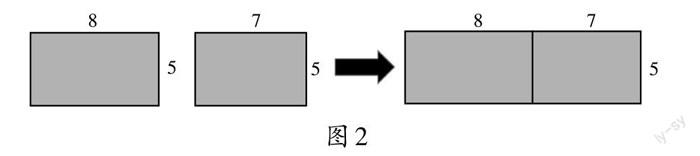
例如，运用乘法分配律进行计算时，学生常常出错，根本原因是学生没有真正理解乘法分配律的原理，出错在所难免。透析代数公式（a+b）×c=a×c+b×c的计算原理，不妨先赋值，再把它移植到两个等宽的长方形中，通过计算两个长方形的面积和来理解这个公式的计算原理。如，赋值为（8+7）×5=8×5+7×5，那么第一个长方形的长赋值为8，第二个长方形的长赋值为7，两个长方形的宽一律赋值为5;先分别求出两个长方形的面积，再求和，那么列式为8×5+7×5（见图2）。这里，因为两个长方形的宽相等，所以不妨将两个长方形以宽边重合拼接，拼组成一个大长方形，从几何变换上理解，此时拼组而成的大长方形面积等于两个小长方形的面积和。这样，大长方形的长变成（8+7），宽仍为5，根据长方形的面积计算公式列式为（8+7）×5。前后用不一样的方法计算出的面积相等，于是就有了（a+b）×c= a×c+b×c。虽然前后意义不一样，但是结果一致。所以，通过数形结合这一数学思想方法，乘法分配律的计算原理便在几何图形组合这个维度上站稳了脚跟，巧妙地突出教学重点、突破教学难点。

在数学教学中，有些算理如能融入几何图形的变换中，利用几何图形的拆分、组合进行面积与长度的运算变换，将图形上的直观变化转化成数字计算上的变化，那么算理就可以被揭示得淋漓尽致，易于学生理解和掌握。学生一看到相关算式脑海里就会浮现出图形，边回顾图形变换边推演算式，进行双重思考。这样通过数形结合，学生既理解了算理，也掌握了算法，真正达到形神兼具的目标。

三、画图策略拓展解题思路

画图是数学解决问题的重要策略，它利用图形展现和记录问题中的数量关系，从而简化题意，便于找到解题思路。同时，画图又是一个抽象、提炼的过程，即删去情境枝叶，提取数量关系主干，并进行简练转述。

1.画图，可以有效突出解题线索

例如，人教版数学教材第十二册《圆柱与圆锥的认识》的练习中有这样一道题：“一个圆锥形沙堆，底面积是28.26平方米，高为2.5米。将其铺在10米宽的便道上，施工要求铺成2厘米厚，能铺多少米？”教学时，部分学生无法进行等体积转换，不知道如何将圆锥形沙堆转化成长方体。于是，教师先引导学生构思如下动图（见图3），再予以点拨：“解题主线是什么？”（沙子的体积始终不变，只是形状发生了变化）“解题的过程是怎样的？”（先求出圆锥形沙堆的体积，再用沙堆的体积除以长方体沙层的横截面面积，就能求出长方体的长）

又如，教学人教版数学二年级的乘法内容后，学生计算时常常在加法和乘法之间不知如何抉择。这时，教师可以通过即时画图，辅助学生理解。如“大头儿子买了3瓶胃动力，又买了5瓶王老吉，一共有几瓶饮料？”，可画示意图4;“大头儿子买了3提胃动力，每提5瓶，一共有多少瓶胃动力？”，可画示意图5。学生通过画图就能直观感知，加法和乘法都是对数量的合并，只是加法是将不同的数量合并，乘法是针对相同的数合并，从而很快弄清加法和乘法的异同点，能正确区分二者的定义。

2.画图，可以迅速厘清数量关系

画图作为一种解题策略，从原先的辅助工具转型升级为课程目标，是抽象问题直观化处理的典型模式，能够快速厘清题中的数量关系，从而找到解题思路。例如，人教版数学教材第九册《稍复杂的方程》中有这样一道例题：“足球表面分为黑白两色外皮，白皮20块，比黑皮的2倍少4块，试问黑皮几块？”这道题的文字表述比较烦琐，难以找到其中的数量关系，但通过画线段图（见图3）分析，就能一目了然。借助线段图，题中足球表面白皮和黑皮的数量关系就直观地呈现在眼前，即白皮数=黑皮数×2-4。此外，此题还可以通过倒序厘清数量关系，即白皮数加上4等于黑皮数的2倍。这样题中的数量关系直观明了，解题思路也就自然呈现出来了。

四、画图策略创新思维方法

数形结合是一种数学思想方法，需要教师在教学中适时渗透，使学生遇到相关问题时能灵活运用，正确地分析与解决问题。数形结合也属于一种解题技巧，可以直接通过画图来解决问题;数形结合还属于一种能力，可借助图形分析问题，创新解题方法，提高解决问题的能力。当学生遇到抽象的数学问题时，能不能熟练地构图、制图、用图，通过画图突破思维瓶颈，寻找到巧妙的解题方法，考验着学生的思维能力。

例如，教学人教版数学教材第十二册《数学思考》的这道题“6个点可以连成多少条线段？8个点呢？”时，就可以通过画图降低难度，总结规律。又如，人教版数学教材第十二册中的“摆一摆，找规律”这道题（见图7）。

如果真要付诸实践，就要准备火柴棒，这显然有难度，且不便于展示，但不摆火柴棒只看图，又不够直观。这时，可通过连续画图分析解题：先画1个正方形，接着往下画第2个、第3个、第4个……当学生画到第4、第5个正方形时，隐含的规律已经昭然若揭：除去第一个正方形需要4条线段，后续的正方形只需要3条线段。有了这个规律，再来解决“摆10个正方形所需要的火柴棒数”“301根火柴棒围成的正方形个数”等问题就轻而易举了。即使要求摆n个正方形所需要的火柴棒数，也不在话下。

五、画图策略助力经验积累

学习画图策略，目的是让学生能灵活运用数形结合这一数学思想方法解决问题，这与“四基”培养的目标是一致的。因此，在小学数学教学中，教师既要关注画图策略在概念内涵学习、算理本质解读、思维方法拓展等方面的运用，又要重视学生基本数学活动经验的积累，让学生在数学学习过程中实现知识与技能的发展，提升学生的數学核心素养。

例如，教学人教版数学教材第五册《长方形和正方形的周长与面积》的练习课时，教师可通过画图帮助学生更好地理解长方形和正方形的周长、面积等概念，让他们在问题探究中更有效地积累学习经验，提高解决问题的能力。

师：看着屏幕上的画面，你获得了什么数学信息？

生1：米老鼠在用竹篱笆围庭院，用了96米的竹篱笆，问有哪些不一样的围法、怎样围面积最大。

生2：这个简单，围成正方形的面积是最大的，这在前面已经学习过，即96÷4=24（米）、24×24=576（平方米）。

生3：这样解答是对的！但是，还有一个问题没有解决，就是有哪些不一样的围法。

生4：刚才的谈论都用到了“长+宽”这个关键点，它是从“（长+宽）×2=长方形的周长”得来的，所以记好、记牢长方形的周长计算公式非常重要。

生5：这些思考都有一定的道理，但它们都不是米老鼠要围成的庭院吧？用竹篱笆围成庭院，难道必须要围4个面吗？

生6：哎呀！还真是的。围庭院可以只围3个面，靠墙的那一面是不用围起来的。

生7：对呀！那3个面共长96米，一条边的长度就是96÷3=32（米），面积最大应该是32×32=1024（平方米）。

……

积累学习经验虽然是学生数学学习的重要任务之一，但是教师在教学中不能忘却新课程强调的一个重要理念，那就是“数学教学必须立足于儿童生活的现实”。笔者以为，这也是智慧教学的一种体现。因此，教师在教学中既要重视学生数学知识的习得，又要关注他们数学活动经验的积累，提高学生解决问题的能力。上述教学，教师意在促进学生关于长方形的周长、面积等知识和经验的激活，并引导学生联系生活实际解决问题，让学生的学习更理性、更高效。

总之，画图策略是数学解决问题的基本策略。在数学课堂中，教师应根据具体的教学内容，利用数与图之间的对应和转化，适时渗透数形结合这一数学思想方法，让学生的思维在抽象思维和形象思维之间灵活转换，将数学问题化抽象为直观、化难为易，从而丰富学生的解题经验，提升学生的思维品质。

[ 参 考 文 献 ]

[1] 叶心慧.从形象到抽象  构建学生优良的思维品质：论画图策略在数学教学中的应用[J].新智慧，2020（30）：127-128.

[2] 孙树通.小学数学教学中画图策略的应用分析[J].新课程导学，2020（8）：20.

[3] 彭芝萍.画图策略在数学教学中的应用[J].江西教育，2019（26）：60-61.

（责编 杜 华）