“实际问题与方程（1）”教法新探

孙晓平

［摘 要］“实际问题与方程（1）”课程中大多直接呈现形如“ax±b=c”的方程问题，为了让学生能够养成主动运用方程解决实际问题的意识，初步学会运用方程，体验方程的先进性，有必要从探寻方程本质入手，引导学生建立模型，最终建立方程思想。

［关键词］方程;应用题;教法革新

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）29-0045-03

关于方程的应用，教材设计了形如“a±x=b”的方程应用题，对于这类运用算术法可以一步到位的应用题，是否有必要用方程来解，或者说用方程来解是否真的更加先进和便捷，仍存在较大争议。一步计算就可以解决的问题被强令用方程来解题，对已经用惯了算术法的学生来说，会感觉有些多此一举，不但要写出烦琐的“解”与“设”，还要将直截了当的数量关系转换成间接的方程表达，把简单的问题复杂化了。这样会导致学生对方程产生排斥心理，更谈不上形成主动应用意识了。学生遇到类似的题目常常会犹豫不决，询问老师如何在方程和算术方法中取舍，因为在他们心目中方程并不是一种解题的技能和工具，反而是一种选择上的负担，用方程解题并不是出于本意而是迫于無奈。之所以会出现这种尴尬的局面，其主因在于学生没有领会到方程的原理和优势所在。鉴于此，在设计与执教“实际问题与方程（1）”这一课时，笔者进行了大刀阔斧的改进与革新。

一、探寻本质，初步体验方程思想

师：果园里，阳桃树有45棵，比水蜜桃树多30棵，水蜜桃树有多少棵？

（学生独立解题，并述说解题思路）

师（隐藏问题，提取条件）：果园里，阳桃树有45棵，比水蜜桃树多30棵。

师：阳桃树和水蜜桃树的棵数是什么关系？

生₁：阳桃树比水蜜桃树多出30棵。

师：没错，你能想办法用一个式子表示这两种果树之间的数量关系吗？

生₂：45-x=30。

生₃：x+30=45。

生₄：45-30=x。

师：水蜜桃树的棵数是未知的，因此可用一个字母代替，以上三个式子均能准确地表示出水蜜桃树和阳桃树的棵数关系。但是，若是非要挑一个最好的式子，你觉得哪一个式子与题目的表述最吻合、最直接？

生₅：生2的式子，因为这个式子是按照题干的语序来呈现其关系的，即“阳桃树的数量-水蜜桃树的数量=相差的30棵”。

生₆：我觉得生3的式子也不差，不过就是反推一下而已，即“水蜜桃树的数量+阳桃树比水蜜桃树多出的30棵=阳桃树的数量”。

师：相对而言，生4的式子一步到位算出结果，与我们的算术法不谋而合，只不过等号后面多了个字母而已。

师：以上的式子在数学里有个专门的称谓——方程。那么解出这个方程就可以顺利得出什么结果？

生₇：水蜜桃树的棵数。

师（小结）：没错，刚才我们没有分析题中的数量关系，也没有进行数量推理，而是将问题转化为一个方程，水蜜桃树和杨桃树的数量关系就蕴含在方程里。我们只要求出方程的解，就可以顺利解决这个问题，这就是方程的神奇之处。

【设计意图】学生运用算术法解题时，他们的第一反应就是根据问题逆向搜寻条件，一步步推理，直到将所有的基本条件集齐了，然后再顺着线索推导出结果，其思维经历了一个正向和逆向的循环往复的过程，逆向溯源，正向推导，从而解决问题。这种方法思维复杂、线索纷繁。而方程思想是先寻找等量关系，这种等量关系往往就在字面上，然后根据这个等量关系建立起抽象的等式，利用含义不特定的数学符号来构建方程。因此，方程的内涵不在于对一个具体情境的刻画，而是对某一类数量关系的描述，一个方程可以解决许多个含有类似数量关系的问题，而算术法解题面对的只是其中的一个具体问题。为了揭示方程的抽象性和概括性，教学从“具体问题”（具体情境中的问题，独立解决时普遍采用算术法）过渡到“抽象问题”（让学生用直接的式子表示数量关系）。在对比中学生明白，算术法需要双向循环推理，而方程只需要顺向推演数量关系，按照题目的语意将数量关系抽象出来就能得到方程，解方程就能得出最终的结果。

二、建立模型，初步形成方程思想

【教学片段1】

师（出示）：张果老种了72棵核桃树，是种植的水蜜桃树的3倍。请你用最直白的式子表示两种果树之间的数量关系。

生1：72÷x=3，3x=72。

师：解出以上两个方程，实际上就等同于求出了什么？

生2：水蜜桃树的数量。

师（完整呈现）：张果老种了72棵核桃树，是水蜜桃树的3倍。水蜜桃树有多少棵？

师：韩国制造了128枚洲际导弹，比朝鲜制造的少14枚。用式子表示韩国和朝鲜拥有洲际导弹数量的关系。

生3：x-14=128，x-128=14。

师：解出上述两个方程，实际上就等同于求出哪个量？

生4：朝鲜制造的导弹数量。

师（完整呈现）：韩国制造了128枚洲际导弹，比朝鲜制造的少14枚。朝鲜制造了多少枚洲际导弹？

师（小结）：刚才我们为了准确表示数量关系，按照题意列出了含有未知数的等式，这些等式就是方程。而按照题意列出的方程，就是对整个数量关系的概括和抽象，因此可以说，方程就是对某种数量关系的抽象表达。

【设计意图】算术法是运用方程法解题的最大障碍，由于先入为主的刻板印象和定式思维，很多学生会固守算术法不放。为了让方程思想渗入学生的数学直觉思维里，教师特地设置两道强化练习题，让学生继续用等式来表示数量关系，进一步强调方程就是抽象化的等量关系的数学本质，让学生初步形成方程思想。

【教学片段2】

师：联合军演中，英国出动60艘军舰，美国的舰船数量是英国的舰船数量的2倍多10艘。请你用式子表示出美国和英国出动军舰的数量关系。

生：2x+10=60，60-2x=10，60÷2-10=x。

（上述三个方程中，很明显前两个方程直接表述美英双方军舰数量的关系，而第三个式子虽然也有未知数，但是意图一步到位地求出英国出动军舰数量，致使数量关系混乱，列式出错）

师：至此，你对方程是否有了新的看法？

师（小结）：从第三个式子来看，如果从结果出发，逆推探寻条件再顺向推导，过程烦琐且容易引起思维混乱。而将结果看作未知数直接顺着题意推演，并抽象出数量关系，则方便得多，理解起来也更轻松。

【设计意图】方程思想的长处在于：无论条件多么错综复杂，只要用一个等量关系串联起所有的数量，那么问题就会变得无比简单。因此无论什么问题，一旦使用方程，就可以脱离復杂的情境，只要专注于解方程，问题自然迎刃而解。在分析本题的数量关系时，当学生根据以往经验直接用算术法列式时，会拿不准到底是先处理“多10”还是先处理“2倍”关系。而此时如果按照题意顺推，就会知道“英国军舰数×2+10艘=美国军舰数”或者“美国军舰数-英国军舰数×2=10艘”，用字母代替未知量，方程就会“浮出水面”。通过对比可以发现，由于有交织在一起的数量关系，用算术法需要经历逆向的复杂推理，而方程则无须推理。通过这样一比较，方程的优势不言而喻。

三、尝试应用，建立完整的方程思想

【教学片段3】

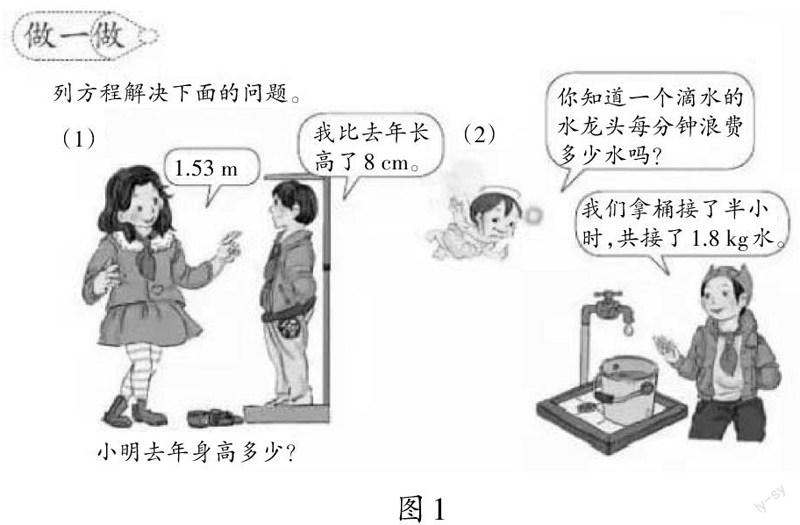
师（出示图1）：老师碰到两个棘手的问题，你能尝试用新学的方程替老师分忧吗？

（要求：先自选方法独立答题，然后展示交流，最后规范方程解题的标准格式）

（1）解：设小明去年身高 x cm。

1.53 m=153 cm

x+8 =153

x+8-8=153-8

x=145

答：小明去年身高 145 cm。

（2）解：设每分钟浪费x kg水。

半小时=30分

30x=1.8

30x÷30=1.8÷30

x=0.06

答：每分钟浪费0.06 kg水。

【设计意图】让学生对方程有更加客观理性的认识，对方程的优势有切身体会，同时掌握用方程解题的标准格式，并真正从心底里接纳和认可方程，形成完整的方程思想。

四、课后反思

史宁中教授曾说，以往的方程教学存在的很大弊病就是南辕北辙：方程的教学本应从具体情境中抽象出方程表达式，通过解方程来间接解决实际问题，而不是先定义抽象的方程，再来赋予其实际意义。本课的教学可谓拨乱反正。

首先，植入并强化。如果仅仅把方程看作一种解题方法，它有时还真不是算术法的“对手”，因为算术法在学生头脑中“盘踞”多年，树大根深，学生第一时间往往会倾向于算术法。从某种程度上说，方程仅仅是一个用“=”连接的等量关系，而算术法中的“=”则可以直接导出运算结果。因此方程应用的教学重点不在解题，而在于传递一种思想：用含有未知数的等式将题中的等量连接起来，抽象成一个可以代表任何类似关系的方程，而解这个方程就可以解决问题。

其次，比较并内化。方程的“解”“设”等步骤，以及运用等式性质解方程的过程看似比算术法麻烦，令学生望而却步，但是，方程的思维过程却是顺向的，简单直白，不易出错，为了这一优势付出点书写上的代价是值得的。教学中设计了“美英联合军演”的情境，足以凸显方程思想的优势。最后通过让学生自选方法独立完成课本“做一做”的第1、2题，检验学生是否真正内化吸收了方程思想的精髓。

诚然，本课通过三个应用题来构建方程模型，让学生初步感知方程的优越性，培养了学生的方程意识。但方程思想的建立是循序渐进的积累过程，并非一日之功，教师还应在日常教学中潜移默化地渗透。

［ 参 考 文 献 ］

[1] 刘晶.厘清等量关系  直击方程本质：“等式与方程”教学设计与说明[J].小学教学参考，2021（17）：68-70.

[2] 张晓玲.以等式的性质为导航使解方程不再难[J].中小学数学（小学版），2021（3）：35-36.

[3] 王正保.“式与方程总复习”教学谈[J].小学数学教育，2021（12）：56-58.

[4] 史宁中.基本概念与运算法则[M]. 北京：高等教育出版社 ， 2013.

[5] 赵晓燕.从“两位数相乘”回到“乘法的意义”：例谈小学数学起点型核心知识教学的重要性[J].江苏教育，2022（33）：11-14.

（责编 罗 艳）