通过有效数学活动设计促进学生数学素养的发展

张化

［摘  要］ 数学活动设计需要以学生的发展为本，以适切问题为载体，以探究为途径，聚焦学生的思维发展与素养提升. 研究者基于数学活动设计的角度，从“串联新旧知识”“重组学习材料”“拓宽知识路径”三个方面进行尝试，以期训练和发展学生的数学素养.

［关键词］ 数学活动；数学素养；思考

“活动”就是由目的、动机、动作联合起来，完成具有一定社会职能的动作综合，当“活动”与数学教学融合，自然会带来其特有的目的性，即“数学活动是学生主动参与的学习活动，是促进学生数学素养发展的探究活动”. 可见，数学活动有着丰富的内涵与特质，倘若实施简单的“为活动而活动”，那自然不是有效的数学活动.

设计合理的数学活动是当前“流行”的教学模式，如何着手设计呢？笔者认为，多元数学活动设计需要以学生的发展为本，以适切问题为载体，以探究为途径，聚焦学生的思维发展与素养提升，让学生经历观察、操作、探讨、交流、猜想、验证等思维过程，发展相应的思维能力，实现素养的发展. 笔者拟从数学活动设计的角度，从“串联新旧知识”“重组学习材料”“拓宽知识路径”三个方面进行尝试，以期训练和发展学生的数学素养.

串联新旧知识来设计活动，促进学生认知结构的完善

数学知识的获得从本质上来说是内化数学知识为认知结构的过程，这就需要教师牢牢把握住新旧知识的连接点，让学生积极主动、生动活泼地学习和探索，让新旧知识相互作用，从而将新知纳入到学生原有认知结构之中，实现充实与完善. 这样一来，则可以帮助学生构建良好的认知结构，也随之促进其掌握认知的策略，使其越学越有趣，越学越乐学，越学越善学.

案例1 直角三角形

活动1：如何将一个等腰三角形分成2个全等三角形？为什么？

学生活动：如图1，作出底边上的高，并证明两个三角形全等，并发现等腰三角形中包含直角三角形.

活动2：观察并思考∠A和∠B间有何数量关系？为什么？

活动3：如图2，已知CD为Rt△ACB斜边AB的高，请试着找一找所有的互余角.

活动4：如图2，已知AF为∠BAC的角平分线，那么△CEF是什么三角形呢？

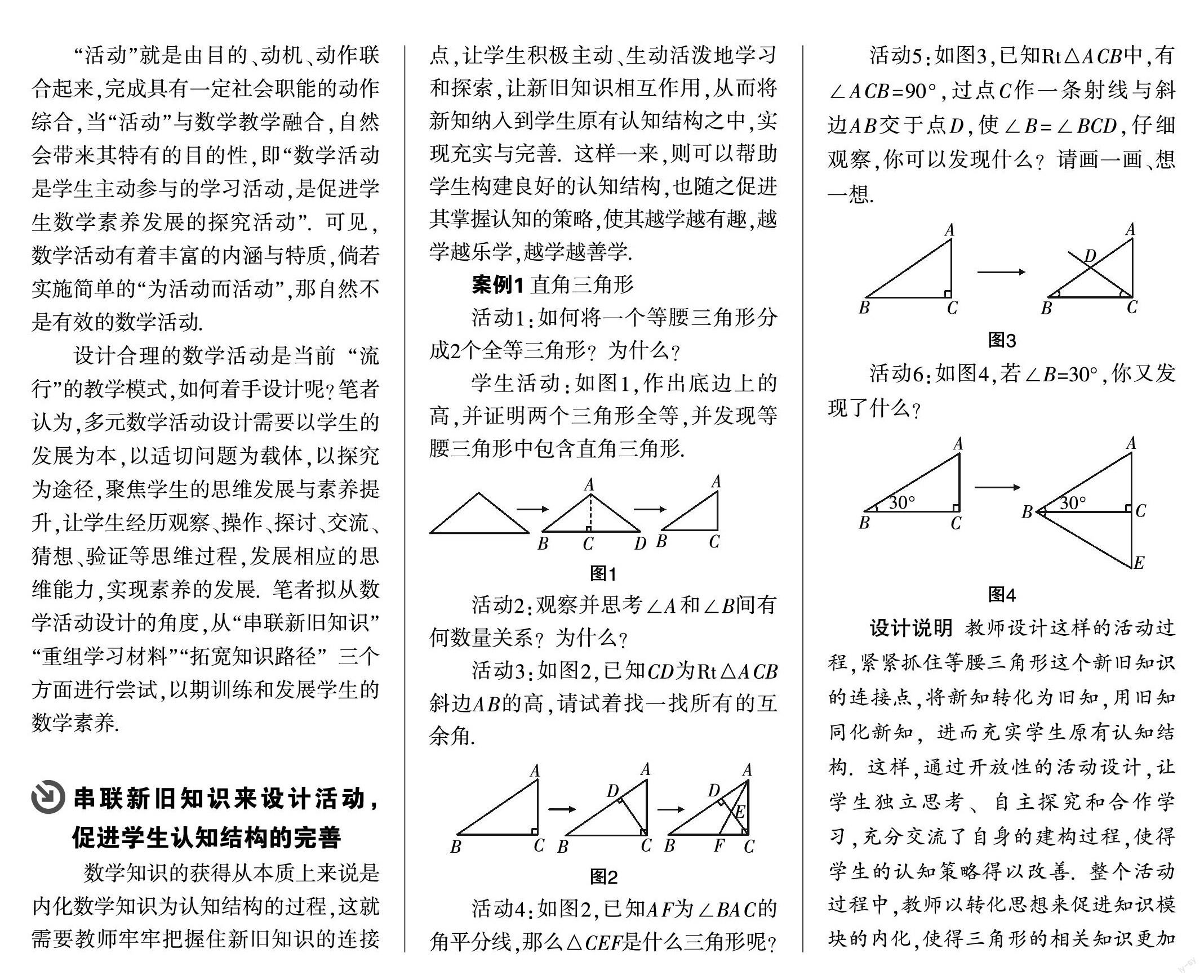
活动5：如图3，已知Rt△ACB中，有∠ACB=90°，过点C作一条射线与斜边AB交于点D，使∠B=∠BCD，仔细观察，你可以发现什么？请画一画、想一想.

活动6：如图4，若∠B=30°，你又发现了什么？

设计说明 教师设计这样的活动过程，紧紧抓住等腰三角形这个新旧知识的连接点，将新知转化为旧知，用旧知同化新知，进而充实学生原有认知结构. 这样，通过开放性的活动设计，让学生独立思考、自主探究和合作学习，充分交流了自身的建构过程，使得学生的认知策略得以改善. 整个活动过程中，教师以转化思想来促进知识模块的内化，使得三角形的相关知识更加丰满、完善和系统，很好地培育了学生的知识建構能力.

重组学习材料来设计活动，实现学生学习力的提升

兴趣是激发学习动机的原动力，也是学生展开探究性学习的前提. 倘若学习材料的呈现能一下就刺激到学生的兴趣，使其在学习材料的牵引下进行数学探究，则可以有效突破难点，实现学习力的提升. 因此，教师在设计活动时要善于选择、重组学习材料，并合理、有序地呈现给学生，让学习材料发挥其最大的教育价值，促成师与生、生与生间的高效互动，推动学生的认知不断向前发展.

案例2 一次函数图像

活动1：观察图5中的“百度天气预报”，从图像中你能发现什么？

师生活动：在对图像的观察中，容易发现其变化趋势，并得出图像是由一个个点组成的.

活动2：你会画一次函数y=x的图像吗？该怎么画？说一说你的想法.

师生活动：第一步，由于函数图像是由点组成的，那么首先是找点和描点；第二步，建系，描点A（1，1），B（2，2），C（3，3）…第三步，观察后发现这些点都在第一、三象限的角平分线上，所以这些点都在同一直线上；第四步，借助几何画板验证上述猜想，以确保理论分析的正确性.

活动3：请用描点法画出一次函数y=x+1的图像，并说一说你的发现.

活动4：你有没有更好的方法画出一次函数y=-5x+20的图像？

活动5：一支长为20厘米的蜡烛，点燃之后每小时燃去5厘米，试写出燃烧时剩下高度y（厘米）与燃烧时间x（时）间的函数关系式. 对照图6，你画出的函数图形正确吗？

活动6：一款新的网红产品A最近十分热销，公司预计2021年前4个月每个月的广告投入y（万元）与月份x（月）间的函数关系满足y=-5x+20，此时的函数图像还是一条直线吗？为什么？

设计说明 学生的兴趣是一节课的主流，教师巧妙重组学习材料设计了具有生活味的“活动串”，让学生经历“有目的地看图—尝试作图—猜想发现—深入验证—建立模型—反思提炼”的过程，在观察、联想和尝试中形成一系列的认知冲突，使得自身的观察发现、科学联想和数学建模的能力得到锻炼. 整个活动过程也是一个高强度的思维训练过程，放手让学生去享受观察、思考、联想、归纳、演绎的过程，可以收获丰富的活动经验，促进学生学习力的自然提升，最终有效培育学生的数学素养.

拓宽知识路径来设计活动，让学生获得思考的活动经验

不少学生认为解题是学习数学的“终极目标”，尽管解题是学生学习的重要课题之一，但对于学生而言，解题活动中积累到的最重要的并不是解题经验，而是在活动中不断积淀下来的思考经验. 由此，笔者认为，教学中教师需要有机融合知识的获取和经验的积累，通过拓宽知识路径来设计数学解题活动，以实现知识向能力的转化，这样，除去解决问题经验本身，学生可能获得的最大收获就是在选择解题策略时的思考活动经验.

案例3 二次函数的专题复习课

活动1：如图7，已知二次函数y=ax2+bx+c图像交x轴于点A（-1，0）和B，交y轴于点C，且有顶点D（1，4），观察该图像，说一说你能发现什么结论？

活动2：点P落在抛物线上，使得S=S，那么这样的点P共有几个？你能求出点P的坐标吗？

活动3：若点P为x轴上方抛物线上的动点，记△BCP的面积是S. 当S为何值时，共有3个满足条件的点P？

活动4：如图8，若点P为x轴下方抛物线y=0.5x2-1.5x-2上的一动点，连接PB和PC，设△PBC的面积是S（且S是整数），那么共有几个满足条件的△PBC？

设计说明 教师用解题活动来拓宽知识路径，引导学生在知识获取基础上自主思考，目的是借助对图像的观察，获得新的发现，形成自己的看法，从而不断地提出新问题、解决新问题、发现新方法、总结新思路，充分体验数学思考的乐趣. 这里，教师给足学生思考、展示、交流的时间和空间，让学生对函数图像的性质形成更深刻的理解，并通过深入挖掘各种方法的优劣性和共性之后，生成解题优化策略. 这样有意义的数学探究活动过程，不仅是学生深度思考的过程，也是深度思维训练的过程，从本质上来说就是数学素养的训练过程，在这个过程中所经历的发现、研究和解决问题的过程，也就是学生获得思考经验的过程.

总之，从学生的数学实际出发，开展训练思维的数学活动，用数学的育人方式对学生进行思考、猜想、语言、合作的训练，可以让学生正确理解知识，实现认知结构的完善，创造性地解决问题，获得思考的活动经验，实现学习力的提升，最终提升数学素养. 笔者认为，日常教学中重视数学活动的设计，对提升学生数学核心素养是极为有益的.