纺织装备行星齿轮传动系统修形研究

莫 帅， 刘志鹏， 罗炳睿， 岑国建， 徐家科， 高瀚君

(1. 天津工业大学 机械工程学院， 天津 300387； 2. 天津市现代机电装备技术重点实验室， 天津 300387； 3. 宁波中大力德智能传动股份有限公司， 浙江 宁波 315301； 4. 北京航空航天大学 虚拟现实技术与系统国家重点实验室， 北京 100191)

现代纺织装备中的大量传动机构都采用齿轮传动，而行星齿轮传动系统作为一种体积小、传动范围大、运转平稳的齿轮传动机构，被广泛应用于各类纺织装备、航空航天、汽车船舶、精密机器人等工业领域。纺织机器人在纺织行业得到了大量应用，其机器人关节采用了各类齿轮减速器，行星减速器作为比较成熟的减速器被广泛应用。在行星齿轮传动系统应用过程中由于制造、装配等误差会造成行星齿轮传动系统在传动中精度降低，产生振动和噪声等缺陷，影响传动系统的传动精度[1]。在齿轮参数和制造装配精度相同的情况下，齿轮修形是一种有效提升齿轮传动平稳性的方法[2]。齿轮修形包括齿廓修形、齿向修形和综合修形，选择合理的修形参数和修形方法可以有效提升行星齿轮传动系统的传动质量[3]。

国内外学者对齿轮修形开展了大量研究。魏静等[4-5]提出了齿廓修形啮合刚度计算模型，建立齿轮修形的刚度与误差非线性模型，分析了不同修形参数对啮合刚度的影响。陈洪月等[6]建立了一种齿廓修形前后的传递误差数学模型，采用多种方法分析了修形参数对传递误差的影响。唐进元等[7]用有限元方法推导出修形齿轮啮合刚度计算方法,利用数值方法阐述了修形量与啮合刚度的定量关系。Ni等[8]提出斜齿轮抛物线修形方法，分析了斜齿轮抛物线修形特性。金亭亭等[9]建立斜齿轮接触分析模型，分析了齿轮接触区的应力分布。张俊等[10]建立行星齿轮动力学模型，以齿轮传递误差波动量为评价指标进行修形研究，提出的修形方法有效改善齿面受载状况，降低了齿轮副的动态传动误差波动量。

目前的修形研究大都只考虑齿廓和齿向的单一修形方案下的某一参数变化，对考虑多种修形的综合方案较少。本文研究某纺织装备行星减速器中第二级行星轮系在齿廓加齿向的综合修形方案下对传动误差、齿面法向力、啮合刚度等特性的影响，来改善行星齿轮传动系统的传动精度和啮合质量，降低传动误差和噪声，对提升纺织装备的传动精度具有一定意义。

1 齿轮修形原理

1.1 齿廓修形原理

齿廓修形在齿顶和齿根处对齿轮渐开线合理修正，去除部分材料，以减小齿轮啮入、啮出冲击，提高齿轮传动精度，降低振动噪声，如图1所示。

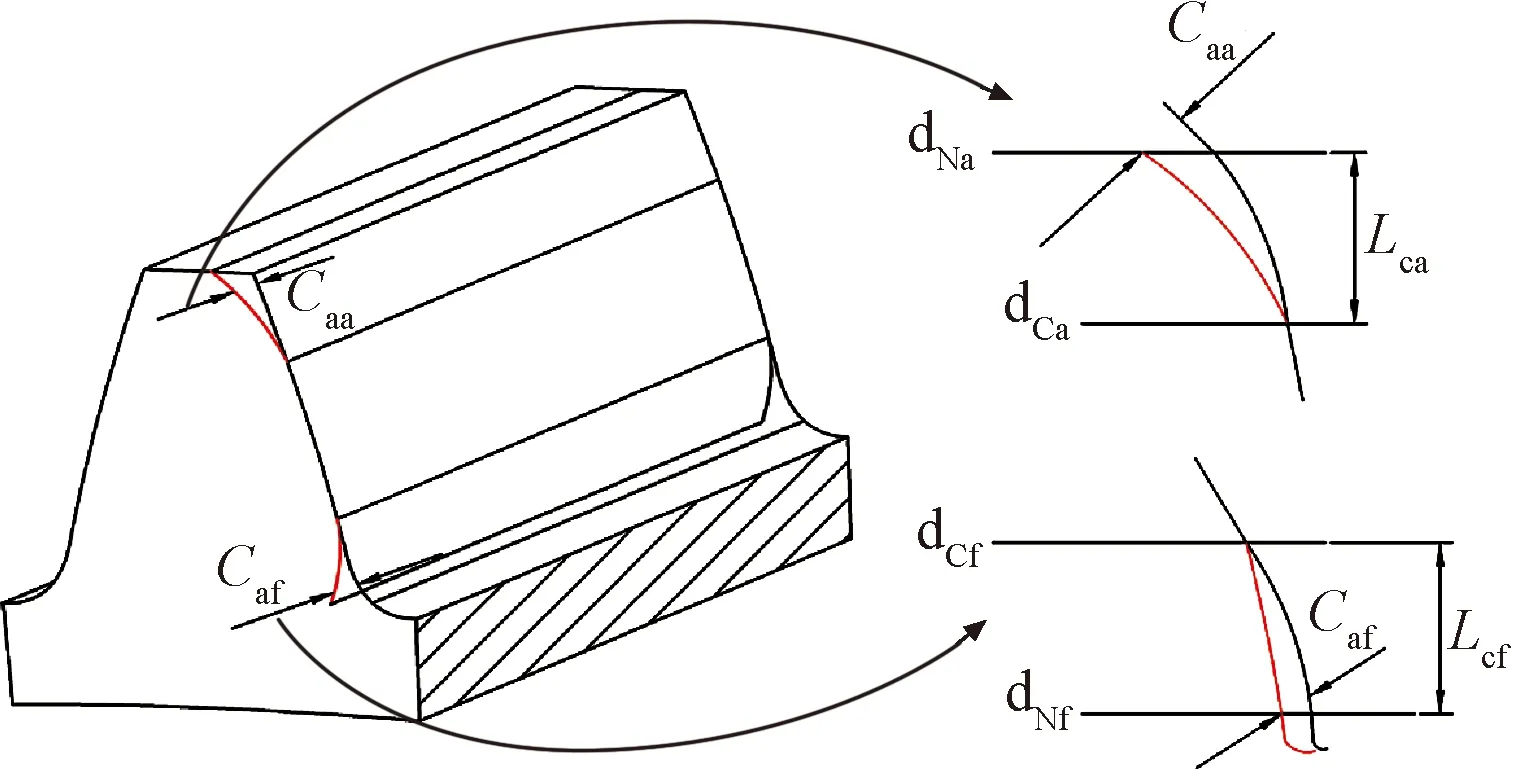
注：图中曲线是修形曲线，Caa为齿顶最大修形量；Caf为齿根最大修形量；dCa为齿顶修形起始点，dNa为终止点；dCf为齿根修形起始点，dNf为终止点；Lca为齿顶修形长度，Lcf为齿根修形长度。图1 齿廓修形示意图Fig.1 Tooth profile modification diagram

修形曲线、修形长度和修形量为齿廓修形参数。其中最大修形量是齿廓修形过程中主要考虑的参数，直接影响修形效果。

标准的齿廓最大修形量为

(1)

式中：KA为工况系数；Ft为圆周力,N；b为齿宽,mm；εα为端面重合度；kγ为综合刚度,N/m。

修形曲线计算公式如下：

(2)

式中:Lcx为修形曲线上任一点到修形起始点的距离，mm；Lc为修形长度，mm；当s=1时为直线修形,s=1.5时为指数曲线修形，s=2时为抛物线修形。

修形长度采用长齿廓修形：

Lc=Pb(εα-1)

(3)

式中：Pb为基圆节距,mm；εα为端面重合度。

1.2 齿向修形原理

图2示出齿向修形示意图。可知齿向修形是在齿宽方向对齿轮表面鼓形修整、齿端修薄，以改善齿轮表面载荷分布，提升齿轮承载能力、降低偏载现象。

齿向修形量Cβx为

(4)

(5)

式中：r为修形圆弧半径,mm；Cβ为最大修形量,μm；x为修形起始点到齿宽的距离,mm。

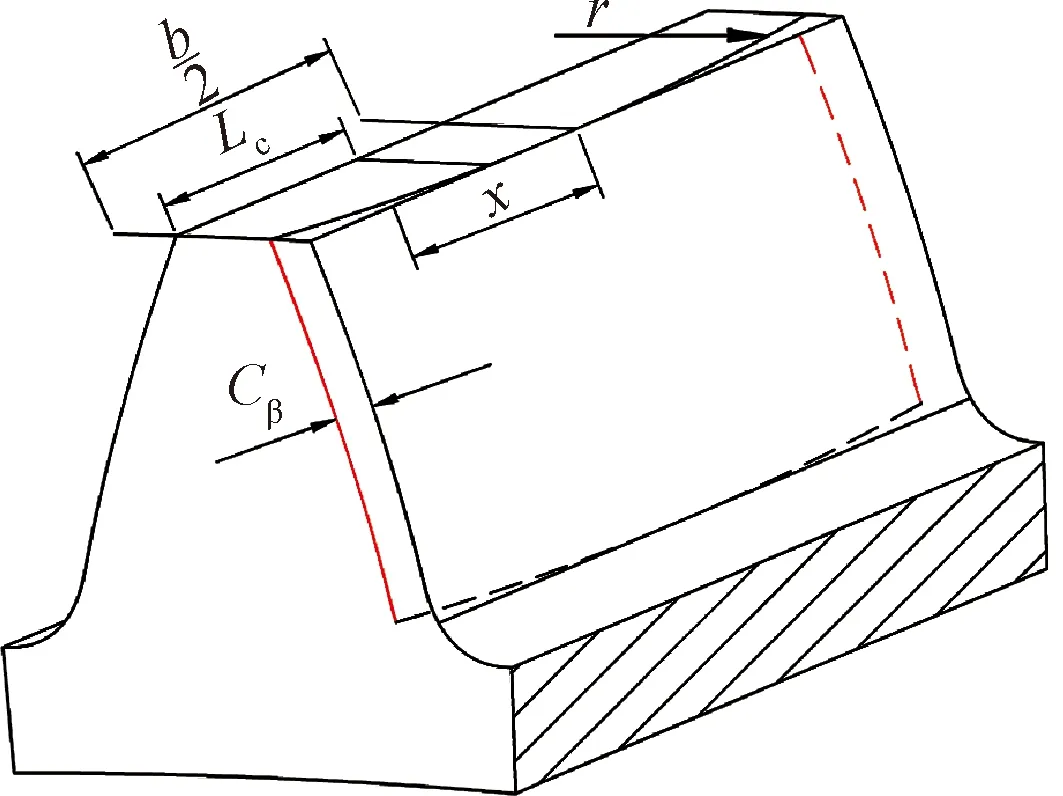
图2 齿向修形示意图Fig.2 Tooth modification diagram

2 行星齿轮传动系统修形评价指标

2.1 静态传动误差

理想齿轮齿面完全共轭，而实际传动中由于齿轮受载变形、制造和安装误差造成实际转角与理想转角产生偏差而引起传动误差(TTE)[11]。传动误差很大程度上影响齿轮传动精度，是齿轮产生振动和噪声的根本所在，因此可通过齿面微观修形来改善齿轮传动状况、降低传动误差波动、减小振动和噪声。

单对齿轮转动角误差表示的传动误差为

(6)

式中：θ1为主动轮转角，rad；θ2为从动轮转角，rad；z1为主动轮齿数；z2为从动轮齿数。

齿轮啮合线上的位移表示的传动误差为

(7)

式中，rb2为从动轮基圆半径,mm。

齿轮修形会引起无负载传动误差(TNLTE) ：

(8)

式中：rb1为主动轮基圆半径，mm;ω1和ω2分别为主从动轮不受外载荷时的转动角速度,rad/s。

齿轮修形后受载时传动误差[8]为

TLTE=rb1θ1-rb2θ2-TNLTE

(9)

行星齿轮传动系统的传动误差可表示为输出轴的实际转动角与其理论转动角之差：

(10)

式中：θ0为输出轴实际转角,rad；φI为输入轴转角,rad。

2.2 齿面法向力

齿轮的齿面法向力可以直接反映齿面受载情况，一般齿轮在传动过程中由于啮入、啮出冲击和载荷变化会使齿面磨损、产生偏载现象,因此进行齿面修形降低啮入和啮出冲击、改善齿面偏载现象、提升齿轮使用寿命显得尤为必要。

斜齿轮的法向力Fn垂直作用于齿面上,齿面法向力Fn计算如下：

(11)

式中：Ft为齿轮圆周力,N；αn为压力角,(°)；β为螺旋角,(°)。

Ft计算如下：

(12)

式中：T为齿轮输入力矩,N·m；d为节圆直径,mm。

2.3 齿轮啮合刚度

齿轮啮合刚度是衡量齿轮修形的重要指标，是齿轮传动系统动力学研究的基础[12]。通过齿面微观修形可使啮合刚度不同程度地降低、其波动变得更加平稳，对齿轮传动系统的减振降噪具有重要意义。

齿轮单位齿宽上的法向力与变形量的比值称为齿轮啮合刚度，啮合刚度计算如下：

(13)

式中：Fn为齿面法向力，N；b为齿宽,mm；δ为齿轮变形量,mm。

齿轮变形量用齿轮转角Δθ表示如下：

δ=Δθrb

(14)

式中：rb为基圆半径,mm。

对齿轮仿真处理提取齿轮转角Δθ，将斜齿轮做切片处理，计算单片齿轮的啮合刚度，求和得到全齿啮合刚度。利用单片齿轮的压力角大小判别齿轮是否进入啮合，第i片啮合齿轮的压力角为

αmin≤αi≤αmax

(15)

式中：αmin为最小压力角，(°)；αmax为最大压力角，(°)。

第1薄片齿轮的转角为φ0，以其为基准，第i片齿轮的转角为

(16)

式中：li为齿面到中心线的距离,mm；β为齿轮螺旋角，(°)；r1为齿轮分度圆半径,mm；z为齿轮轮齿编号。

第i片齿轮压力角αi计算如下：

αi=arctan(αmin+inv(αmin)+φ0)

(17)

齿轮总时变啮合刚度计算如下：

(18)

式中,N为齿轮切片数。

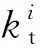
(19)

3 行星齿轮传动系统修形

3.1 行星齿轮传动系统模型

本文以某型号精密行星减速器的第二级行星齿轮为研究对象，输入扭矩100 N·m，其他设计参数见表1。其数字化样机如图3所示。

表1 第2级行星齿轮参数Tab.1 Parameters of the second stage planetary gear

图3 精密行星减速器Fig.3 Precision planetary reducer

3.2 行星齿轮传动系统修形方法

由于行星轮系中行星轮同时与太阳轮和内齿圈啮合，本文只对行星轮进行修形研究，采用齿顶、齿根圆弧修形和齿向鼓形综合修形方法。

3.2.1 齿廓修形

均方差可以反映一组数据的离散程度，选择不同的修形曲线，计算传动误差均方差用以反映不同修形方式时的传动误差波动量，从而选取一种最佳的修形曲线。传动误差均方差计算如下：

(20)

式中：TTEi为啮合周期内任意时刻的传动误差；TTEm为平均传动误差。

选取1.1节所述的不同修形曲线，保持修形量和修形长度不变研究不同修形曲线对传动误差的影响,结果如图4所示。直线修形相比修形前传动误差波动幅值明显降低，而其他2种修形方式传动误差波动反而更大，因此本文选择直线修形方式。

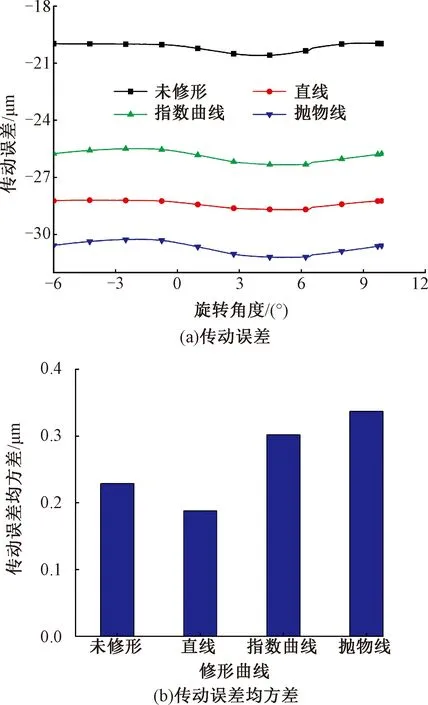
图4 不同修形曲线时传动误差和传动误差均方差Fig.4 Transmission error (a) and mean square error of transmission error (b) under different modification curves

先不考虑其他修形方式，仅进行齿廓修形，齿顶修形量和齿根修形量Ca分别取0、5、8、10、14、18 μm，得到第二级行星轮系传动误差、齿轮法向力、啮合刚度的变化规律。

图5(a)和(b)分别示出齿顶修形量和齿根修形量Ca取上述不同修形量时太阳轮与行星轮、行星轮与内齿圈的传动误差。由图可见，随着修形量的增大，太阳轮与行星轮、行星轮与内齿圈的传动误差峰峰值波动降低，当修形量为14 μm时，传动误差峰峰值波动最小。

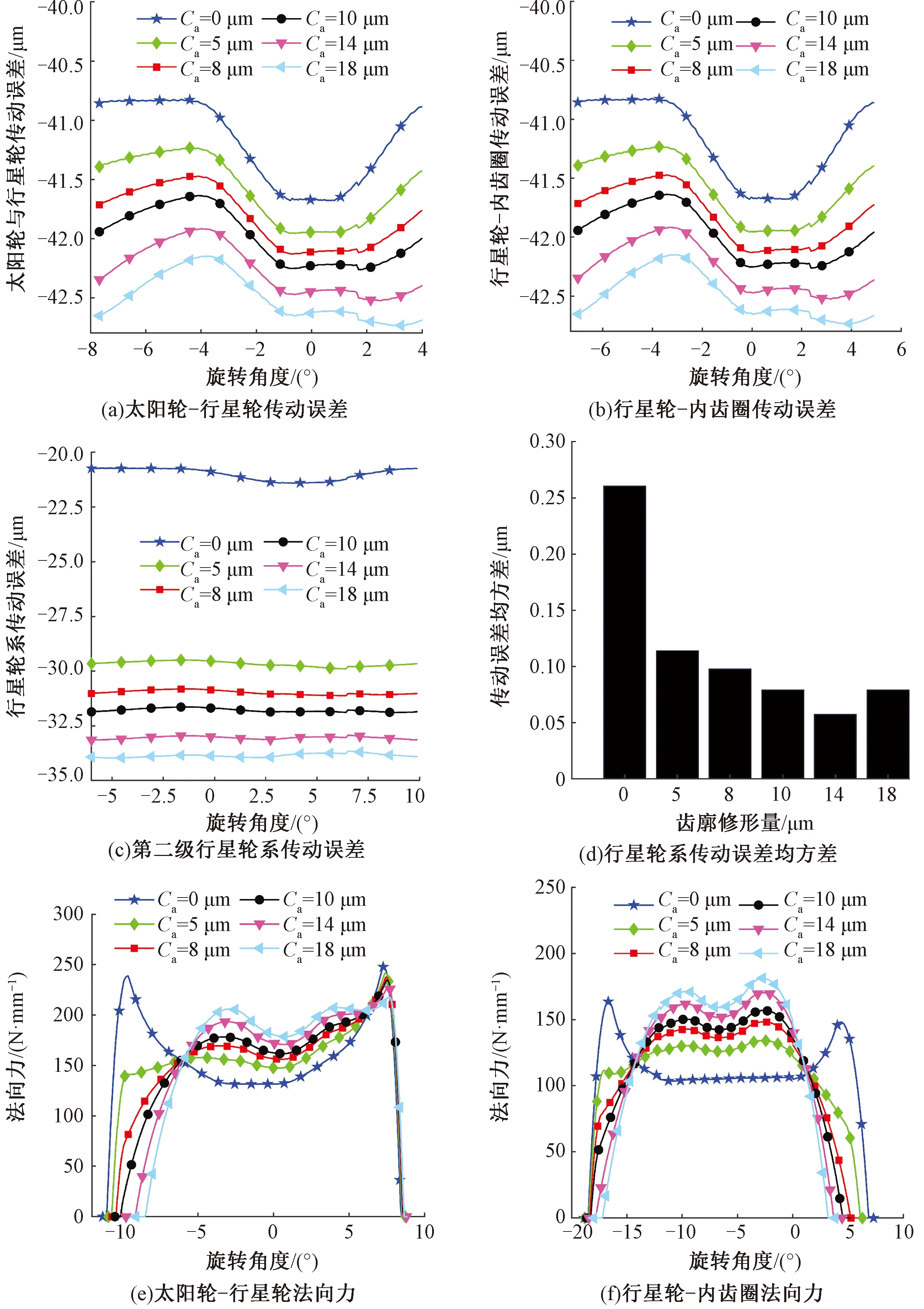
图5 不同齿廓修形量的传动误差和法向力Fig.5 Transmission error and normal force of different tooth profile modification. (a) Sun gear-planetary gear transmission error; (b) Planetary gear-ring gear transmission error; (c) Transmission error of the secondary planetary gear train; (d) Mean square error of planetary gear train transmission error; (e) Sun gear-planetary gear normal force; (f) Planetary gear-inner gear ring normal force

Ca取不同值的第二级行星轮系传动误差和传动误差均方差如图5(c)和(d)所示，未修形时行星轮系的传动误差峰峰值较高，波动较大，当Ca小于14 μm时，传动误差峰值波动随着修形量的增加逐渐降低，波动趋于平稳，当Ca为14 μm时，传动误差均方差达到最小，即传动误差波动最小，当Ca继续增大时，传动误差峰峰值波动开始增大，与未修形的传动误差均方差减小约77.97%。

图5(e)和(f)分别示出太阳轮与行星轮、行星轮与内齿圈的法向力。由图可见，未修形时太阳轮与行星轮、行星轮与内齿圈啮入、啮出有较大冲击，此时的法向力较大，传动不平稳，随着修形量的增加法向力变化趋于平缓，当Ca为14 μm时法向力缓慢增大，太阳轮与行星轮法向力在180 N/mm附近波动，行星轮与内齿圈法向力在150 N/mm附近波动，齿轮啮出时逐渐降低，整个传动过程较修形前法向力有所降低，在啮入、啮出时变化较平缓，对齿轮的冲击降低。

图6、7分别示出齿顶修形量和齿根修形量Ca分别为0，5，8，10，14，18 μm时的啮合刚度。由图可见，Ca增大时，啮合刚度降低。综合考虑传动误差和齿轮法向力，选取最佳齿顶修形量和齿根修形量Ca为14 μm。

图6 太阳轮-行星轮啮合刚度Fig.6 Sun gear-planetary gear meshing stiffness

图7 行星轮-内齿圈啮合刚度Fig.7 Planetary gear-ring gear meshing stiffness

3.2.2 齿向修形

在无齿廓修形情况下，齿向鼓形量Cβ分别取0,2,5,8,10,12 μm，由于得到的各修形量下的啮合刚度曲线完全重合，即齿向鼓形对行星齿轮传动系统各齿轮刚度影响不大，所以给出了太阳轮与行星轮、行星轮与内齿圈和第二级行星轮系传动误差、齿面法向力的变化规律。

图8(a)、(b)、(c)和(d)分别示出Cβ取上述修形量时的传动误差曲线图和传动误差均方差。由图可见，修形前传动误差峰峰值波动较大，Cβ从2 μm增加到10 μm时的传动误差均方差逐渐减小，当Cβ=10 μm时达到最小，波动量最小，此后开始增大，与未修形相比传动误差均方差减小了约65.12%。

图8(e)和(f)分别示出Cβ分别为0,2,5,8,10,12 μm时的法向力曲线。由图可见Cβ增大，齿轮法向力随即增大，参考传动误差，Cβ取10 μm时的法向力波动量较小，第二级行星轮系传动较稳定。故最佳Cβ为10 μm。

图8 不同齿向修形量的传动误差和法向力Fig.8 Transmission error and normal force of different tooth modification amount. (a) Sun gear-planetary gear transmission error; (b) Planetary gear-ring gear transmission error; (c) Transmission error of the secondary planetary gear train; (d) Mean square error of planetary gear train transmission error; (e) Sun gear-planetary gear normal force; (f) Planetary gear-inner gear ring normal force

3.2.3 齿廓与齿向综合修形

Ca取14 μm，保持齿廓修形长度和修形量不变，取不同齿向鼓形量Cβ，由3.2.2节内容可知，齿向鼓形对行星轮系各齿轮刚度影响不大，得到太阳轮与行星轮、行星轮与内齿圈和第二级行星轮系传动误差、齿面法向力变化规律。

图9(a)、(b)、(c)和(d)示出Cβ分别为0、2、5、8、10、12 μm时的系传动误差均方差。由图可见，太阳轮-行星轮、行星轮-内齿圈的传动误差峰峰值在Cβ增大时逐渐减小，第二级行星轮系的传动误差均方差逐渐减小，当Cβ为10 μm时达到最小，即传动误差波动最小，与修形前的传动误差均方差相比减小了约79.78%，此后开始增大。

由图9(e)和(f)可见Cβ增大，齿轮法向力随即增大，鼓形量Cβ为10 μm时的法向力波动量较小，第二级行星轮系传动较稳定。

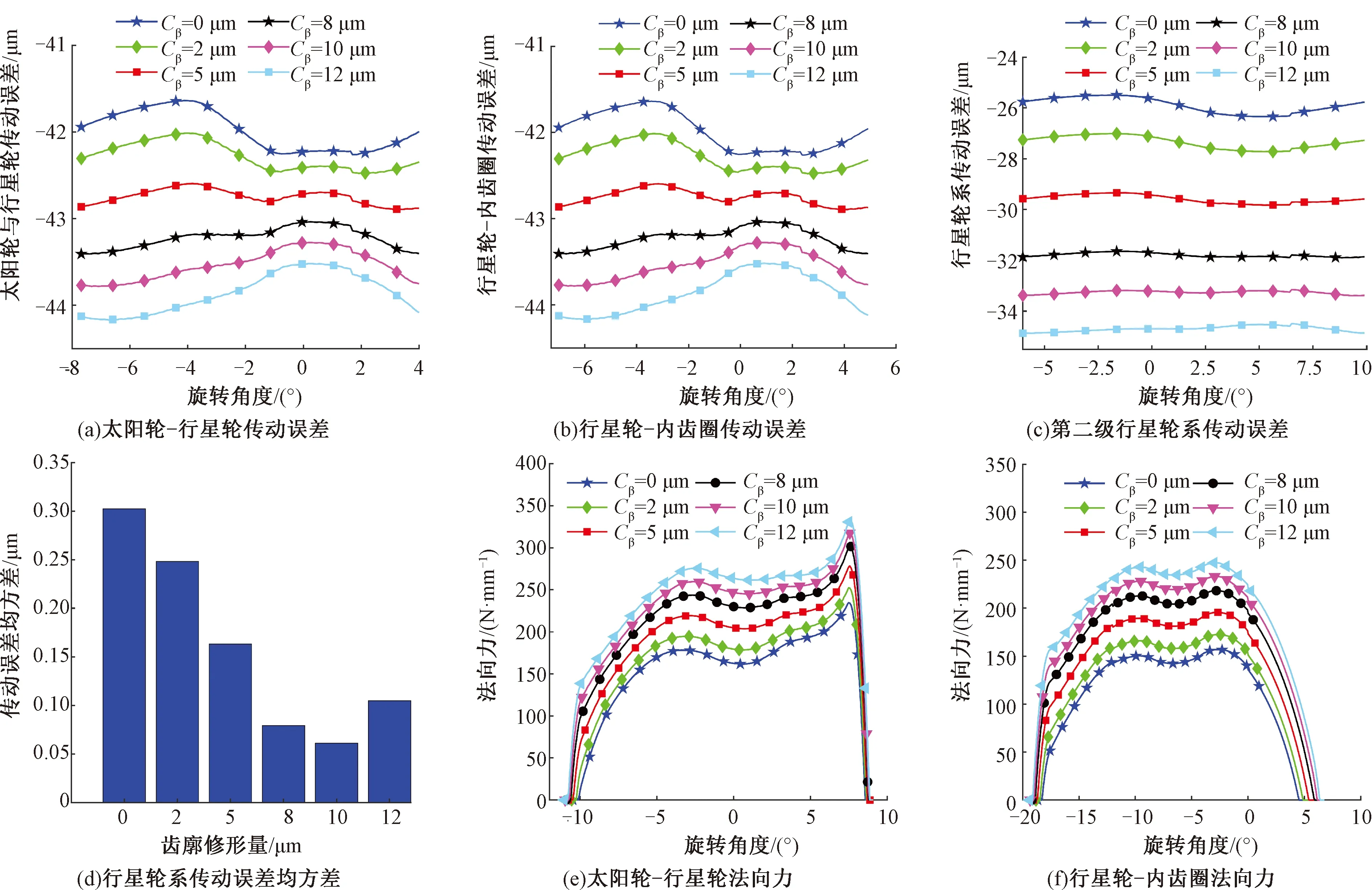
图9 综合修形不同修形量的传动误差和法向力Fig.9 Transmission error and normal force of comprehensive modification with different modification amount. (a) Sun gear-planetary gear transmission error; (b) Planetary gear-ring gear transmission error; (c) Transmission error of the secondary pla-netary gear train; (d) Mean square error of planetary gear train transmission error; (e) Sun gear-planetary gear normal force; (f) Planetary gear-inner gear ring normal force

综上所述，得到行星轮的齿面载荷分布如图10所示，修形前齿面存在边缘接触，齿面载荷分布不规则，修形后的齿面载荷呈椭圆形均匀分布。由此，精密行星减速器第二级行星轮系的最佳齿顶修形量和齿根修形量为14 μm，最佳齿向鼓形量为10 μm。

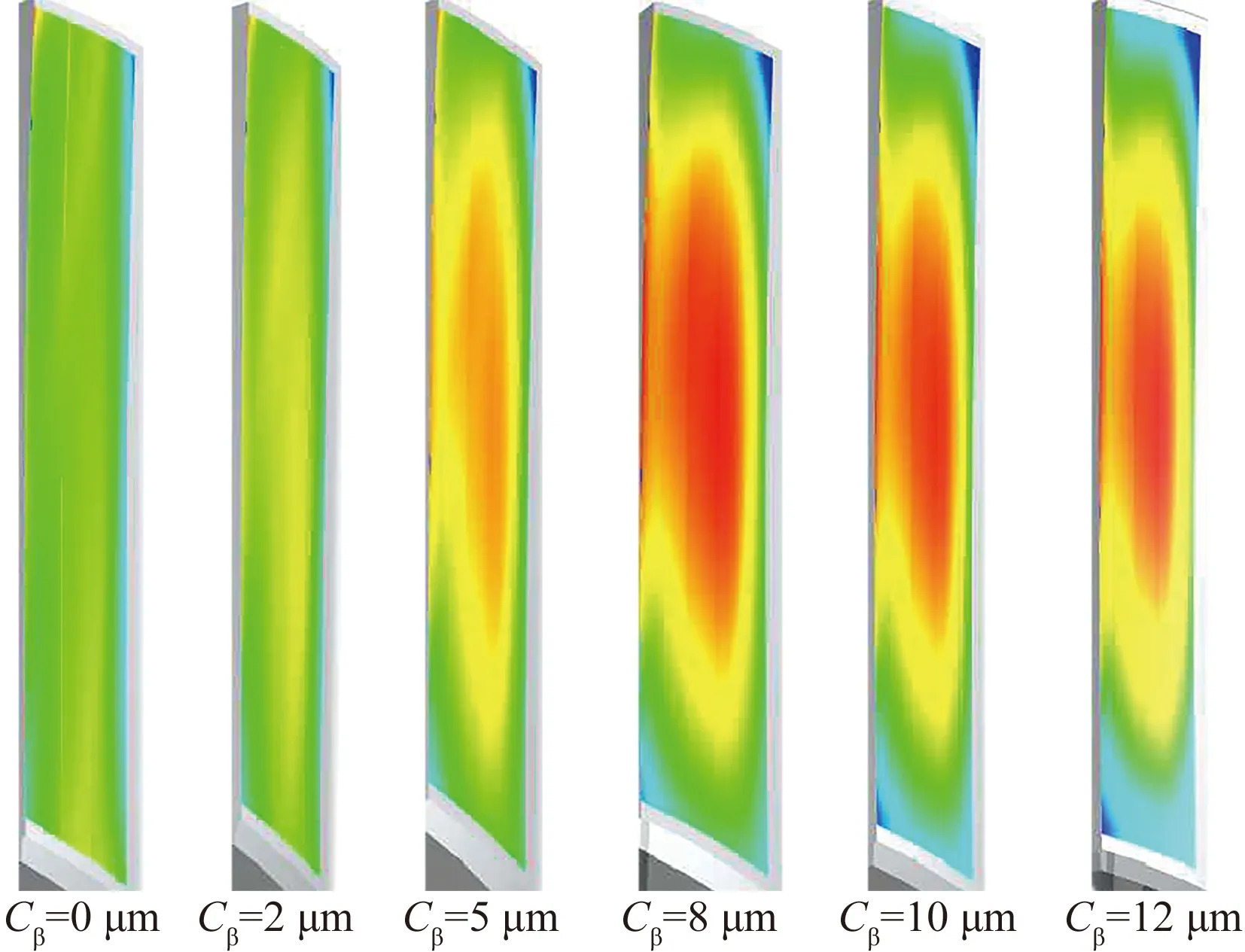
图10 行星轮接触区Fig.10 Contact area of planetary gear

4 结 论

1)本文以纺织装备用行星减速器第二级行星轮系传动误差、齿轮法向力、齿轮啮合刚度为修形评价指标，进行了齿廓和齿向鼓形修形研究，综合对比不同修形量下的各参数变化，得出行星齿轮传动系统最佳修形量。

2)在输入载荷不变的情况下，通过改变行星轮的修形量改善传动啮合质量，研究发现，当齿顶、齿根修形量为14 μm，齿向鼓形量为10 μm时，齿轮法向力有所降低、变化平稳，降低了行星齿轮传动系统的噪音。

3)通过对齿廓修形和齿向鼓形修形的综合研究，得出行星齿轮传动系统的传动误差峰峰值由修形前的0.68 μm降为修形后的0.25 μm，降低了约63%，使行星齿轮传动系统传动趋于平稳，为精密行星减速器的减振降噪分析提供参考依据。

FZXB