探讨高职院校公共基础课教学改革与创新研究新途径

摘 要：“高等数学”是一门公共基础课程，其概念较多，逻辑性强，内容比较抽象。针对如今的生源基础和当代大学生的特点，传统的“满堂灌”教学模式已经不适合他们的学习模式，高等数学学困生人数增加，这与高职院校人才培养目标相违背。高职教师有必要在现今形势下对高等数学授课内容进行教学改革和创新研究，探讨高等数学课程教学改革与创新研究新途径，激发学生的学习兴趣，提升教学质量，达到事半功倍的教学效果。

关键词：高等数学;教学改革;创新研究

The Reform in Eduction and Innovation Research of Basic Course under

the Visual of Course Politics

——Take Advanced Mathematics for an Example

Zhao Lijuan

Nanjing Institute of Railway Technology JiangsuNanjing 210031

Abstract：As a basic course，advanced mathematics contains a lot of concepts，has powerful logic，it’s contents are abstract.In connection with the foundation of students resources and the characteristics of contemporary college students，the traditional "cramming education" mode is not fit for the students，the number of poor students in advanced mathematics learning is increasing，it was against the personnel training objective of vocational college.It is the time for teachers to probe and take an a reform in eduction and innovation research of advanced mathematics under the visual of course politics.Arousing the students interests，promoting the quality of teaching，achieving maximum results with little effort.

Keywords：advanced mathematics;reform in eduction;innovation research

1 高職院校“高等数学”课程进行教学改革与创新研究的必要性

“高等数学”是高职院校的一门公共基础课程，其覆盖面广，内容比较抽象。高职院校的理工类各专业和文管类大部分专业学生都学习高等数学课程。学生经常会抱怨自己中学的数学基础较弱，到了大学为什么还要学习高等数学？学习高等数学到底有什么用？教师经常会劝解学生：“高等数学可以培养学生的逻辑思维和抽象思维能力，培养学生用数学相关知识解决实际问题的能力。此外，高等数学是为专业课服务的，后续的专业课程学习要用到高等数学的相关知识。”这种比较宽泛的解释学生后续可能会逐渐感知并理解，但短时间内还是无法深刻体会到学习高等数学的必要性，学生学习的积极性依旧不高。此外，高等数学知识内容比较抽象，知识体系较为系统，学生前期的高等数学基础如果没有打好，后续学习起来将会相当吃力，长此以往，学习兴趣将会减弱。

近几年，高职院校学生基础参差不齐，生源多样化，单独招生学生占的比例越来越大，大部分同学基础较弱，缺乏有效的学习计划和方法，学习目标模糊，在一定程度上会产生自卑心理。此外，这部分学生自主投入性偏低，学习自信心不足，畏惧抽象概念的学习，对数学类课程学习普遍兴趣不高。他们缺乏独立思考意识，自学能力较弱，没有养成归纳、总结知识内容和数学思想方法的习惯，积极主动性较低，容易产生厌学心理，传统的“满堂灌”教学方式已经不适合他们。

作为00后，当代大学生对计算机软件充满好奇，计算机基本操作比较熟练，对实事比较感兴趣，比较关注所学课程与专业课程的紧密联系，较为享受图片和动画带来的视觉上的冲击。因此，教师需要进行反思，针对不同生源状况，结合现今形势，借助计算机软件，探讨高职院校高等数学课程教学改革与创新研究新途径，优化教学设计，重新设计教学环节，有效地传授知识，就像“盐溶于水”，使学生自然而然地接收，达到润物细无声的效果[1]，激发学生学习兴趣，提升教学质量。

2 如何在现今形势下进行高等数学教学改革与创新研究

高等数学的学习是一个漫长而艰苦的过程，当中有的学生可能会畏惧而停止不前。教师可以在课前优化教学设计，课堂中讲解部分数学史的内容，引导学生学习优秀的科学家凡事追求完美与卓越的工匠精神，增强文化自信和学生的自信心，引导鼓励学生不畏艰难，追求科学进步和科技创新。此外，教师可讲解“共和国勋章”获得者于敏的事例，引导学生明白：做任何事情，只要确定目标，勇于追求理想，纵然前方困难重重，也要敢于坚持，寻求解决方法，不忘初心，牢记使命，砥砺前行，方得始终。

高数课教师应与专业课教师多交流沟通，合作建立专业案例库。针对不同专业的学生，在实际授课环节，展现专业案例，引导学生用数学的思维和方法解决实际问题，让学生切实感受到数学源于实践，又回归于实践。增强学生的专业自信，感觉学习高等数学的实用性，激发学习的求知欲，增强自信心。

在实际授课之前，教师应多观看网络微视频，多创新多思考，寻找实际授课内容中切实有用的教学案例，与所授课内容紧密联系起来，重新优化设计教学环节，提高课程教学质量。

作为高等数学课程的主要教学内容之一，定积分的概念是微积分学的重要内容，它是进一步学习定积分的性质和计算的基础。传统教学模式中，定积分的概念部分文字叙述繁多，内容抽象、枯燥，学生难以深刻理解。作为公共基础课“高等数学”的授课教师，我们以定积分的概念一课为例，探讨高等数学授课内容教学改革与创新研究新途径。

2.1 源于实践：通过两个实例引入曲边梯形的定义

教师可以多关注一些新闻，挖掘一些实事，寻找与所教内容的紧密结合点，激发学生的求知欲。在讲解定积分的概念之前，教师可以展示长江三峡溢流坝的图片，给学生视觉上的冲击和震撼。教师讲解建造这样的大坝，需要根据体积准备相关材料，而要计算它的体积，就需要我们尽可能准确地计算它的断面面积。长江三峡溢流坝断面的形状是根据物理中流体力学的原理设计的，它上面一段是抛物线，中间是直线，而下面是一段圆弧线。教师抛出问题：从数学的角度，如何计算长江三峡溢流坝断面面积呢？让学生切实感受到数学的实用性，学习数学的必要性。

此外，与专业相结合，教师可以播放高铁发展变化的一些图片，让学生感受高铁日新月异的变化，中国高铁现如今已经成为世界上一张靓丽的名片，激发学生的民族自豪感。教师抛出问题：那么在高铁车头的建造中，如何求车头截面面积呢？

通过两个具体案例，吸引学生的注意力，激发学生的学习兴趣，让学生深刻感受到数学是用来解决实际问题的，增强学生对所学专业的热爱。通过提炼两个实际问题的共同特征，引出曲边梯形的定义，培养学生的探究意识和抽象概括能力，引导鼓励学生不畏艰难，追求科学进步和科技创新。教师抛出问题：如何计算曲边梯形的面积？引发学生思考。

2.2 方法探究：通过割圆术的思想，探究求解曲边梯形面积的方法

教师引导学生回忆，在前面学习极限时，我们曾提到过刘徽的割圆术，其主要思想是：以直代曲，无限细分，无限逼近。我们能否用同样的思想来求曲边梯形的面积呢？教师启发引导学生尝试用割圆术的思想求解曲边梯形的面积，学生小组讨论，头脑风暴，课堂气氛激烈。

教师引导学生分小组思考：当分割越细时，小矩形面积和近似代替曲边梯形的面積是否越精确？两者之间的误差如何衡量？小组成员之间再次进行激烈探讨，越思考，越讨论，思路越清晰。

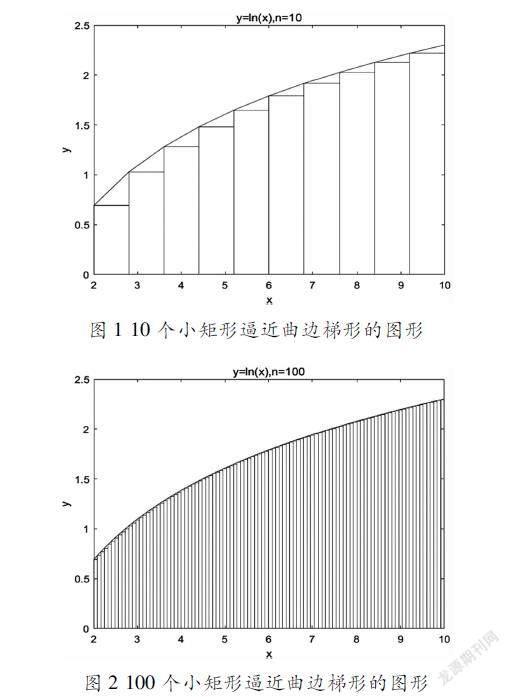
以自然对数y=lnx为例，教师可以现场编写数学软件Matlab绘制10个小矩形逼近曲边梯形的图形，100个小矩形逼近曲边梯形的图形的Matlab代码，简单的几行代码，绘制出两个图形，如图1和图2所示，让学生切实感受到数学软件的神奇，借助图形直观，深刻感受到分割越细时，小矩形面积和近似代替曲边梯形的面积越精确。

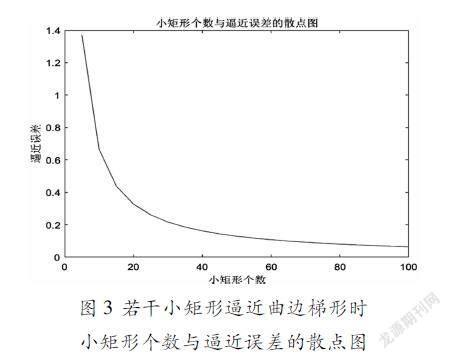
借助图3图形直观展示，教师进行归纳总结：当分割越细时，小矩形面积和近似代替曲边梯形的面积越精确，误差越来越小。借助Matlab软件图形直观展示，给学生视觉上的冲击，将晦涩难懂的知识点变得易懂，让学生明白其中蕴含的道理。

2.3 大胆验证：给出求解曲边梯形面积的步骤

受割圆术思想的启发，结合Matlab软件图形直观展示，探究出求解曲边梯形面积的四个步骤：分割、近似、求和、取极限。引导学生从有限中认识无限，从近似中认识精确[2]，深刻体会和明白求解曲边梯形面积的四个步骤。

通过讲解求解曲边梯形面积的四个步骤，引导学生明白一个个小矩形的面积微不足道，但是无穷多个小矩形的面积和却是整个曲边梯形的面积。作为当代的大学生，做事要一步一个脚印，脚踏实地，不畏艰难曲折，勇往直前，努力实现自己的人生目标[3]。此外，求解曲边梯形面积的第四步引导学生明白，做任何事情，应当坚持不懈，持之以恒，这样就会和目标越来越近。

教师根据单调有界准则及两边夹法则，从数学的角度解释：当分割很细时，如果小矩形面积和的极限存在，为一定值，那为何曲边梯形的面积就等于这个定值？解答学生的困惑，使学生对所学内容更加清晰明了、豁然开朗。

2.4 抽象概括：提炼概括出定积分的概念

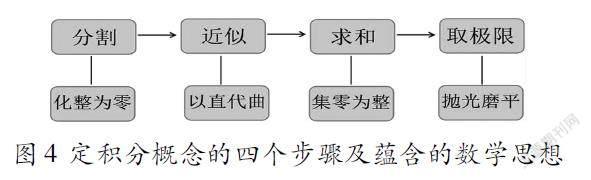
结合求解曲边梯形面积的方法和步骤，抛开问题的实际意义，抓住它们在数量关系上共同的本质，进行抽象概括，提炼出定积分的概念，引导学生明白定积分概念的四个步骤及蕴含的数学思想，如图4。

教师强调定积分概念的注意事项：定积分的概念中，区间的分割是任意的，点的选取也是任意的。

定积分的思想让同学们明白，再复杂的事情都是由简单的事情组合起来的，需要我们用智慧去分解，理性平和地去做事[4]。

2.5 归于实践：计算高铁在某个时间段走过的路程

将前面所得定积分的概念应用于实际问题，如计算高铁在t1到t2时间段走过的路程s，它实际上就是瞬时速度v（t）关于时间t在区间t1到t2上的定积分：

让学生再次领略和感受定积分的魅力，增强学生对专业学习的热爱，切实感受数学是来源于实践，并回归于实践的。

结语

本文以高等数学课程中定积分的概念为例，分析了如何在教学中实施教学改革与创新研究。在定积分的概念实际教学中，結合案例导入、Matlab软件、图形、动画等多种教学手段，给学生视觉上的冲击，让学生在轻松欢快的氛围中理解逼近的数学思想，掌握定积分的概念。此外，我们要在平时的教学中，多思考总结，基于一个细节灵魂拷问，深度追问。

高等数学作为一门通识课，课时多，战线长，覆盖面广，学生和教师都极其重视。教师应当充分把握机会，以教学内容为载体，借助信息化软件技术，探讨高职院校高等数学课程教学改革与创新研究新途径，传播给学生正能量，使学生在学到知识的同时，激发和提高自己的学习兴趣，变“要我学”为“我要学”。高职院校高等数学类课程的教学改革与创新研究是一项长期而艰巨的任务，需不断摸索前进。

参考文献：

[1]梁克东.高职课程思政建设应厘清“三重逻辑”.《中国教育报》职教周刊·教改探索，2021119，7.

[2]仇默.《定积分的概念》教学设计[J].青少年日记（教育教学研究），2014，92.

[3]杨丽娅.高等数学课程中融入思政元素的途径分析[J].现代商贸工业，2021：129130.

[4]刘淑芹.高等数学中的课程思政案例[J].教育教学论坛，2018：3637.

基金项目：南京铁道职业技术学院校级课题“‘课程思政’视角下高校公共基础课教学改革与创新研究”（Yr21 0003）;南京铁道职业技术学院《高等数学》课程思政教改研究课题（2019KCSZ018）;南京铁道职业技术学院校级大学生创新项目“互联网背景下高职院校学生自发性学习共同体构建与研究”（yxkc202133）;江苏省高等学校自然科学研究面上项目“最优化问题的信赖域算法研究及其应用”（21KJB110018）;南京铁道职业技术学院“青蓝工程”资助项目（2020、2021）;江苏省“青蓝工程”资助项目（2020、2021）

作者简介：赵利娟（1986— ），女，河南洛阳人，理学博士，南京铁道职业技术学院讲师，研究方向：数值最优化、数学教育。