题组建构 质疑反思 变式拓展

杭静　刘继光

单元复习是初中数学单元教学中的一个重要环节，为此，不同版本的初中数学教材在每个章节最后都精心设计了“小结与思考”，供教师教学时使用。如何用好这个重要的课程资源呢？特级教师陈德前为我们展示了苏科版七年级上册第三章“代数式”单元复习课，他巧用教材资源，采用“题组建构，质疑反思，变式拓展”的教学策略，效果非常好，值得我们学习和借鉴。

【片段一】题组建构，演练回顾建构单元知识体系

师：同学们在阅读教材中“小结与思考”的基础上，复习了本章的知识点，下面请你们用所掌握的知识和方法解决下列问题，然后与大家分享。

问题1：列代数式：①a的1 1/2倍与2的差______;②m的3倍除以n的商______;③笔记本每本x元，碳素笔每支y元，买5本笔记本和5支碳素笔共花费_____元。

师：哪个同学愿把自己的答案与大家分享？

生：①3/2a-2;②3m/n;③（5x+5y）。

师：大家有不同意见吗？

生：①能表示为1 1/2a-2吗？②能表示为3m÷n吗？

生：不能，代数式的字母系数为带分数时要化为假分数，除法要写成分数的形式。

师：（5x+5y）能不加括号吗？

生：不能，當代数式是和差的形式，且后面带有单位时一定要加括号。

师：我们可以用字母表示，列出代数式（板书：字母表示数，代数式，列代数式），反过来也可以赋予代数式实际意义。

问题2：你们能再说出代数式“5x+5y”表示的实际意义吗？

生：青菜每千克x元，萝卜每千克y元，5x+5y表示买5千克青菜和5千克萝卜的总价。

师：很好！我们可以发现：一个代数式表示的实际意义是丰富多彩的。

问题3：在上面的代数式①3/2a-2;②3m/n;③（5x+5y）中再增加代数式④-5;⑤ab2;⑥a2b+b2a-1。你们能说其中的整式的序号吗？说明理由。

生：①③④⑤⑥是整式，因为整式由单项式和多项式组成。（教师板书：整式、单项式、多项式）

问题4：在这些整式中，单项式有哪些？多项式有哪些？怎样区分它们？

生：④⑤是单项式，①③⑥是多项式，含有加减运算的整式都是多项式。

……

问题5：计算代数式⑤与⑥的差，求出当a=-1，b=2时这个代数式的值（板书：求代数式的值），并由此说明整式加减的一般步骤（板书：整式的加减）。

生：先列式ab2-（a2b+b2a-1），再去括号，然后合并同类项，得-a2b+1，代入求得值为-1。整式加减的一般步骤是：有括号的先去括号，然后合并同类项。（教师板书：去括号，合并同类项）

师：求代数式的值要注意两点：一是格式要规范，二是代入数值时要“对号入座”，省略的符号要“恢复原状”。

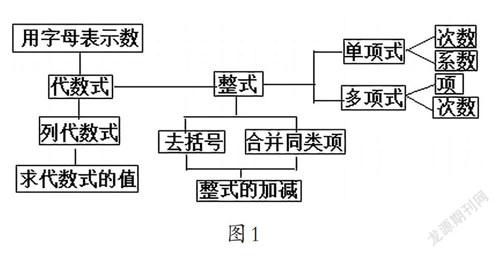
【赏析】教学中，陈老师精心设计了一个层层递进、环环相扣的题组，让学生通过题组来回忆代数式的有关知识，在学生交流分享题组答案时，教师要求其说出解决问题时应用的知识点，这样就能有效防止学生死记硬背知识点，较好地检查学生对有关知识的掌握和运用情况，使得基础知识的复习科学合理、简捷高效。在学生说出应用的知识点的同时，陈老师机智地将重要的知识点加以板书，最后巧妙地构建出“代数式”全章的整体知识结构图（如图1），这样“代数式”所有的知识点就条理清晰地呈现在学生面前，有效地帮助学生完成了所学知识“由厚到薄”的内化过程，这一教学方式蕴含着无限的教学智慧。

【片段二】质疑反思，深化对重难点知识和易错点知识的理解

师：对照知识结构图，结合上面题组，联想相关知识要点，你们还有哪些困惑吗？

（学生提出典型困惑问题，教师及时地把它们板书到黑板上）

生：ab2-a2b-b2a是多项式，但合并后的-a2b又是单项式，它到底是多项式还是单项式？

生：多项式a2b+b2a-1的系数是什么？

生：-a2b+1中常数1的次数是多少？

师：同学们提出的这些问题都很有价值！请大家对这些问题先独立思考，再组内讨论，然后派代表进行全班交流。

（学生思考、讨论后交流）

生：我认为ab2-a2b-b2a是单项式ab2、-a2b、-b2a的和，它应是多项式，而不应看它运算后的结果。

生：由于多项式各项系数不一定相同，因此对多项式不谈系数，只谈某一项的系数。

生：由于常数项中不含字母，因此对常数项应该不谈次数。

师：对！整式分类以原始算式为依据，以“是否有加减运算”为标准，不以运算结果来判断。对于多项式不谈系数，对常数项不谈它的次数。下面是部分同学完成上述题组时出现的错误情况，请你们做小老师，找出其中错误的原因，告之解题中的注意点。（板书：解题注意点）

（1）ab2的次数为2，没有系数;

（2）a2b+b2a-1的常数项为1;

（3）a2b-a2b=（1-1）a2b=a2b;

（4）a2b-（a2b+b2a-1）=a2b-a2b+b2a-1。

生：按照约定，a的次数为1而不是0，因此ab2的次数为1+2=3，而不是2;系数是1，它省略了，不是没有系数。解题时要注意有关约定。（教师板书：约定要遵守）

生：a2b+b2a-1的常数项为-1，项要连同前面的符号。解题时概念要清晰。（教师板书：概念要清晰）

生：a2b-a2b=（1-1）a2b=0a2b=0，所以结果应为0，而不是a2b。解题时书写要规范。（教师板书：书写要规范）

生：a2b-（a2b+b2a-1）=a2b-a2b+b2a-1中等号左边括号前面是“-”，去括号后+b2a和-1这两项要改变符号;a2b与-a2b是同类项，要继续合并。解题时过程要符合算理。（教师板书：过程要合理）

师：很好！同学们不仅找到了错误的原因，而且指出了避免错误的注意点。

【賞析】质疑反思是本节课的一个特色，教学中，陈老师设计了两个层次：一是对照结构图，结合练习题，联系知识点，让学生提出自己的困惑。学生提出了不少问题，陈老师从中精心选择了很有价值的3个问题，再通过独立思考、小组讨论、全班交流、教师点拨等方式来解疑释惑，给学生足够的活动时间与空间。这样的教学活动，学生的参与度高，思考积极，踊跃发言，清晰了模糊认识，取得了极佳效果。二是由教师根据学生解决题组问题时出现的典型错误，以错题集的形式出示了4个典型问题，通过错例来引领学生分析错因，不仅有效地暴露了学生知识上的缺陷，而且使学生对错因有了理性的认识，避免“屡纠屡犯”，让学生的错误成了最有价值的教学资源。

【片段三】变式拓展，提升学生的关键能力

师：请同学们考虑一下，你们准备怎样解决课本中的这道复习题？

图2是一组数值转换机的示意图，若输入x的值为-3，则输出的值为_________。

生：直接代入，利用有理数的运算来解决问题，答案为13。

生：运算程序[3x2-1/2，输入x=-3，可得答案为13。

师：正确！如果给出的是一个代数式的值，又如何求另一个代数式的值呢？

变式1 如果a-b=2，那么代数式1+2a-2b的值是_____。

师：先独立思考，再小组交流，看谁的解法多？并推选代表对不同解法进行讲解。

生：将b当作已知数，解方程得a=b+2，则原式=1+2（b+2）-2b=1+2b+4-2b=5。

生：把1+2a-2b变形为1+2（a-b），然后把a-b=2整体代入，原式=1+2×2=5。

生：取b=0，则a=2，当a=2，b=0时，原式=1+2×（2-0）=5。

师：真不简单！同学们已经学会从多角度看待给定的条件，并能运用多种方法进行计算。方法一：从常数角度看待字母b，用含b的代数式表示a代入求值。方法二：从整体角度看待a-b，从求值式中变换出a-b，整体代入，十分简捷。方法三：从特殊与一般的关系看待字母a和b，巧取b=0，则a=2，代入求值式计算。

变式2 如果代数式5a+3b的值为-4，那么代数式2（a+b）+4（2a+b）的值是多少？

生：5a+3b的值为-4，即5a+3b=-4，而2（a+b）+4（2a+b）=10a+6b，因此用上述三种方法均可解答。

师：对！上述三种解法都适用，但本题是解答题，一般不能用特殊值法，但可用于检验。可见，在解答数学题时要注意解法的多元性。

变式3 小明说：“请任意想一个数，把这个数乘2后加8，然后除以4，再减去你原来所想的那个数的1/2，我可以知道你计算的结果是2。”你们相信吗？

生：设任意想的那个数为x，根据题意，得代数式1/4（2x+8）-1/2x，化简得2。所以这个代数式的值与x的取值无关，即x取任意一个数，这个代数式的值都是2。

……

【赏析】这个教学环节是本节课的高潮阶段，陈老师通过一道典型的课本习题，一题多解，一题多变，多中求简，多中选优，梯度鲜明，拾级而上，从直接将数值代入求代数式的值，到用关系式求代数式的值，整体求代数式的值，再到转化变形后运用上述方法求代数式的值，一气呵成，在不断进行的变式拓展中渗透了数学思想方法。在这个过程中，陈老师先让学生独立完成练习，再分组交流，充分讨论不同的解法，培养学生多角度思考问题的习惯，然后全班学生共同总结解题的体验和收获，从思想方法的高度加以提炼，帮助学生进一步巩固所学内容，训练基本技能，领悟思想方法，积累基本经验，不断提升学生综合运用知识分析问题和解决问题的关键能力，发展学生的数学核心素养。

（作者单位：江苏省兴化市板桥初级中学）

投稿邮箱：405956706@qq.com

本文系江苏省教育科学“十三五”规则2020年度课题“苏科版初中数学教材‘小结与思考’设计价值与使用策略研究”（课题编号：D/2020/02/232）的阶段性研究成果。